Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-10T15:15:39.993Z Has data issue: false hasContentIssue false
  • English
  • Français

Bergman norm estimates of Poisson integrals

Published online by Cambridge University Press:  22 January 2016

Boo Rim Choe ,
Hyungwoon Koo  and
Heungsu Yi
Boo Rim Choe
Affiliation:
Department of Mathematics, Korea University, Seoul 136–701, Korea, choebr@semi.korea.ac.kr
Hyungwoon Koo
Affiliation:
Department of Mathematics, Hankuk University of Foreign Studies, Yongin, Kyungki-Do 449-791, Korea, koohw@maincc.hufs.ac.kr
Heungsu Yi
Affiliation:
Department of Mathematics, Research Institute of Basic Sciences, Kwangwoon University, Seoul 139–701, Korea, hsyi@math.kwangwoon.ac.kr
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

On the half space Rn × R+, it has been known that harmonic Bergman space bp can contain a positive function only if 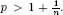. Thus, for 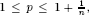, Poisson integrals can be bp-functions only by means of their boundary cancellation properties. In this paper, we describe what those cancellation properties explicitly are. Also, given such cancellation properties, we obtain weighted norm inequalities for Poisson integrals. As a consequence, under weighted integrability condition given by our weighted norm inequalities, we show that our cancellation properties are equivalent to the bp-containment of Poisson integrals for p under consideration. Our results are sharp in the sense that orders of our weights cannot be improved.

Keywords

Primary 31B05Secondary 31B1032A3530D55
Type
Research Article
Information
Nagoya Mathematical Journal , Volume 161 , March 2001 , pp. 85 - 125
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 2001

References

[1] Axler, S., Bourdon, P. and Ramey, W., Harmonic Function Theory, Springer-Verlag, New York, 1992.CrossRefGoogle Scholar
[2] Ramey, W. and Yi, H., Harmonic Bergman Functions on Half-Spaces, Trans. Amer. Math. Soc., 348 (1996), 633–660.CrossRefGoogle Scholar
[3] Stein, E., Harmonic Analysis, Princeton Mathematical series 43, Princeton University Press, Princeton, NJ, 1993.Google Scholar
[4] Stein, E. and Weiss, G., Fourier Analysis on Euclidean Spaces, Princeton University Press, Princeton, NJ, 1971.Google Scholar
[5] Yi, H., Harmonic Bergman Functions on Half Spaces, Ph. D Thesis, Michigan StateUniversity, 1994.Google Scholar