Hostname: page-component-6bf8c574d5-w79xw Total loading time: 0 Render date: 2025-02-18T23:53:04.431Z Has data issue: false hasContentIssue false
  • English
  • Français

BERNSTEIN–SATO ROOTS FOR MONOMIAL IDEALS IN POSITIVE CHARACTERISTIC

Part of: (Co)homology theory General commutative ring theory

Published online by Cambridge University Press:  20 March 2020

EAMON QUINLAN-GALLEGO Open the ORCID record for EAMON QUINLAN-GALLEGO [Opens in a new window]
EAMON QUINLAN-GALLEGO*
Affiliation:
Department of Mathematics, East Hall, 530 Church Street, 48109Ann Arbor, MI, USA email equinlan@umich.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Following the work of Mustaţă and Bitoun, we recently developed a notion of Bernstein–Sato roots for arbitrary ideals, which is a prime characteristic analogue for the roots of the Bernstein–Sato polynomial. Here, we prove that for monomial ideals the roots of the Bernstein–Sato polynomial (over 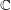$\mathbb{C}$) agree with the Bernstein–Sato roots of the mod 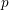$p$ reductions of the ideal for 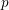$p$ large enough. We regard this as evidence that the characteristic-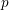$p$ notion of Bernstein–Sato root is reasonable.

MSC classification

Primary: 13A35: Characteristic $p$ methods (Frobenius endomorphism) and reduction to characteristic $p$; tight closure
Secondary: 14F10: Differentials and other special sheaves; D-modules; Bernstein-Sato ideals and polynomials
Type
Article
Information
Nagoya Mathematical Journal , Volume 244 , December 2021 , pp. 25 - 34
Check for updates
Copyright
© 2020 Foundation Nagoya Mathematical Journal

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Partially supported by the National Science Foundation grant DMS-1801697 and by the Ito Foundation for International Education Exchange.

References

Bernstein, J. N., Analytic continuation of generalized functions with respect to a parameter , Funct. Anal. Appl. 6 (1972), 26–40.Google Scholar
Bitoun, T., On a theory of the b-function in positive characteristic , Selecta Math. 24 (2018), 3501–3528.10.1007/s00029-017-0383-xCrossRefGoogle Scholar
Blickle, M., Mustata, M. and Smith, K. E., Discreteness and rationality of F-thresholds , Michigan Math. J. 57 (2008), 43–61.Google Scholar
Blickle, M. and Stäbler, A., Bernstein–Sato polynomials and test modules in positive characteristic , Nagoya Math. J. 222 (2016), 74–99.Google Scholar
Budur, N., Mustaţă, M. and Saito, M., Bernstein–Sato polynomials of arbitrary varieties , Compos. Math. 142 (2006), 779–797.10.1112/S0010437X06002193CrossRefGoogle Scholar
Budur, N., Mustaţă, M. and Saito, M., Roots of Bernstein–Sato polynomials for monomial ideals: a positive characteristic approach , Math. Res. Lett. 13 (2006), 125–142.Google Scholar
Hara, N. and Yoshida, K.-I., A generalization of tight closure and multiplier ideals , Trans. Amer. Math. Soc. 355 (2003), 3143–3174.CrossRefGoogle Scholar
Hochster, M. and Huneke, C., Tight closure, invariant theory, and the Briançon–Skoda theorem , J. Amer. Math. Soc. 3 (1990), 31–116.Google Scholar
Kashiwara, M., B-functions and holonomic systems , Invent. Math. 38 (1976/77), 33–53.10.1007/BF01390168CrossRefGoogle Scholar
Kashiwara, M., “ Vanishing cycle sheaves and holonomic systems of differential equations ”, in Algebraic Geometry (Tokyo/Kyoto, 1982), Lecture Notes in Mathematics 1016 , Springer, Berlin, 1983, 134–142.CrossRefGoogle Scholar
Leykin, A. and Tsai, H., Dmodules: functions for computations with $D$ -modules. Version 1.4.0.1.Google Scholar
Malgrange, B., Sur les polynômes de I. N. Bernstein, Séminaire Équations aux dérivées partielles (Polytechnique), (1973–1974). talk:20.Google Scholar
Malgrange, B., “ Polynômes de Bernstein–Sato et cohomologie évanescente ”, in Analysis and Topology on Singular Spaces, II, III (Luminy, 1981), Astérisque 101 , Soc. Math. France, Paris, 1983, 243–267.Google Scholar
Mustaţă, M., Bernstein–Sato polynomials in positive characteristic , J. Algebra 321 (2009), 128–151.10.1016/j.jalgebra.2008.08.014CrossRefGoogle Scholar
Mustaţă, M., Takagi, S. and Watanabe, K.-I., “ F-thresholds and Bernstein–Sato polynomials ”, in Proceedings of the Fourth European Congress of Mathematics, European Mathematical Society, Zürich, 2005, 341–364.Google Scholar
Quinlan-Gallego, E., Bernstein–Sato theory for arbitrary ideals in positive characteristic, preprint, 2019, arXiv:1907.07297.Google Scholar
Sato, M., Theory of prehomogeneous vector spaces (algebraic part)—the English translation of Sato’s lecture from Shintani’s note , Nagoya Math. J. 120 (1990), 1–34; Notes by Takuro Shintani, Translated from the Japanese by Masakazu Muro.10.1017/S0027763000003214CrossRefGoogle Scholar
Stadnik, T., The Lemma on $b$ -functions in Positive Characteristic, preprint, 2012, arXiv:1206.4039.Google Scholar