1 Introduction
The Brill–Noether theorem of Göttsche and Hirschowitz [Reference Göttsche and HirschowitzGHi94] shows that a general stable bundle on  $\mathbb{P}^{2}$ has at most one nonzero cohomology group. On a Hirzerbruch surface
$\mathbb{P}^{2}$ has at most one nonzero cohomology group. On a Hirzerbruch surface  $\mathbb{F}_{e}$ the situation is not so simple—the section of negative self-intersection can cause every bundle with given numerical invariants to have interesting cohomology. In this paper, we determine necessary and sufficient conditions on numerical invariants which ensure that the general stable bundle on
$\mathbb{F}_{e}$ the situation is not so simple—the section of negative self-intersection can cause every bundle with given numerical invariants to have interesting cohomology. In this paper, we determine necessary and sufficient conditions on numerical invariants which ensure that the general stable bundle on  $\mathbb{F}_{e}$ has at most one nonzero cohomology group. Essentially equivalently, we also compute the Betti numbers of a general stable bundle.
$\mathbb{F}_{e}$ has at most one nonzero cohomology group. Essentially equivalently, we also compute the Betti numbers of a general stable bundle.
We then show that the general stable sheaf on  $\mathbb{F}_{e}$ has a special resolution by direct sums of line bundles. These resolutions generalize the Gaeta resolution of a general sheaf on
$\mathbb{F}_{e}$ has a special resolution by direct sums of line bundles. These resolutions generalize the Gaeta resolution of a general sheaf on  $\mathbb{P}^{2}$, and can be viewed as giving unirational parameterizations of moduli spaces of sheaves [Reference EisenbudEis05, Reference GaetaGae51]. Thus, these resolutions are a convenient tool for describing a general sheaf. As a consequence of the Brill–Noether theorem and the Gaeta-type resolution, we completely determine when a general stable bundle on a Hirzebruch surface is globally generated. The case of
$\mathbb{P}^{2}$, and can be viewed as giving unirational parameterizations of moduli spaces of sheaves [Reference EisenbudEis05, Reference GaetaGae51]. Thus, these resolutions are a convenient tool for describing a general sheaf. As a consequence of the Brill–Noether theorem and the Gaeta-type resolution, we completely determine when a general stable bundle on a Hirzebruch surface is globally generated. The case of  $\mathbb{F}_{1}$ implies an analogous result for
$\mathbb{F}_{1}$ implies an analogous result for  $\mathbb{P}^{2}$ which sharpens a theorem of Bertram, Goller and Johnson [Reference Bertram, Goller and JohnsonBGJ16]. These theorems play crucial roles in the construction of theta and Brill–Noether divisors and in the study of Le Potier’s Strange Duality Conjecture. We also anticipate they will be useful in the study of ample vector bundles on these surfaces.
$\mathbb{P}^{2}$ which sharpens a theorem of Bertram, Goller and Johnson [Reference Bertram, Goller and JohnsonBGJ16]. These theorems play crucial roles in the construction of theta and Brill–Noether divisors and in the study of Le Potier’s Strange Duality Conjecture. We also anticipate they will be useful in the study of ample vector bundles on these surfaces.
Let  $\mathbb{F}_{e}$ denote the Hirzebruch surface
$\mathbb{F}_{e}$ denote the Hirzebruch surface  $\mathbb{P}({\mathcal{O}}_{\mathbb{P}^{1}}\oplus {\mathcal{O}}_{\mathbb{P}^{1}}(e))$, where
$\mathbb{P}({\mathcal{O}}_{\mathbb{P}^{1}}\oplus {\mathcal{O}}_{\mathbb{P}^{1}}(e))$, where  $e$ is a nonnegative integer. The Picard group
$e$ is a nonnegative integer. The Picard group  $\operatorname{Pic}(\mathbb{F}_{e})=\mathbb{Z}E\oplus \mathbb{Z}F$ is generated by the class of a fiber
$\operatorname{Pic}(\mathbb{F}_{e})=\mathbb{Z}E\oplus \mathbb{Z}F$ is generated by the class of a fiber  $F$ of the projection
$F$ of the projection  $\unicode[STIX]{x1D70B}:\mathbb{F}_{e}\rightarrow \mathbb{P}^{1}$ and the class of the section
$\unicode[STIX]{x1D70B}:\mathbb{F}_{e}\rightarrow \mathbb{P}^{1}$ and the class of the section  $E$ with self-intersection
$E$ with self-intersection  $E^{2}=-e$. Let
$E^{2}=-e$. Let  $H$ denote an ample class on
$H$ denote an ample class on  $\mathbb{F}_{e}$ and let
$\mathbb{F}_{e}$ and let  $\mathbf{v}$ be the Chern character of a positive rank
$\mathbf{v}$ be the Chern character of a positive rank  $\unicode[STIX]{x1D707}_{H}$-semistable sheaf. We call
$\unicode[STIX]{x1D707}_{H}$-semistable sheaf. We call  $\mathbf{v}$stable for brevity. Let
$\mathbf{v}$stable for brevity. Let  $M(\mathbf{v}):=M_{H}^{\unicode[STIX]{x1D707}\text{-}\mathit{ss}}(\mathbf{v})$ be the moduli space of
$M(\mathbf{v}):=M_{H}^{\unicode[STIX]{x1D707}\text{-}\mathit{ss}}(\mathbf{v})$ be the moduli space of  $\unicode[STIX]{x1D707}_{H}$-semistable sheaves with Chern character
$\unicode[STIX]{x1D707}_{H}$-semistable sheaves with Chern character  $\mathbf{v}$. By a theorem of Walter [Reference WalterWal98], the moduli space
$\mathbf{v}$. By a theorem of Walter [Reference WalterWal98], the moduli space  $M(\mathbf{v})$ is irreducible, and therefore it makes sense to talk about a general sheaf of character
$M(\mathbf{v})$ is irreducible, and therefore it makes sense to talk about a general sheaf of character  $\mathbf{v}$. If
$\mathbf{v}$. If  $r(\mathbf{v})\geqslant 2$, then Walter additionally shows the general sheaf in
$r(\mathbf{v})\geqslant 2$, then Walter additionally shows the general sheaf in  $M(\mathbf{v})$ is a vector bundle.
$M(\mathbf{v})$ is a vector bundle.
Our first theorem generalizes the Göttsche–Hirschowitz Theorem.
Theorem 1.1. Let  $\mathbf{v}$ be a stable Chern character on
$\mathbf{v}$ be a stable Chern character on  $\mathbb{F}_{e}$ with rank
$\mathbb{F}_{e}$ with rank  $r(\mathbf{v})\geqslant 2$ and total slope
$r(\mathbf{v})\geqslant 2$ and total slope
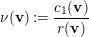 $$\begin{eqnarray}\unicode[STIX]{x1D708}(\mathbf{v}):=\frac{c_{1}(\mathbf{v})}{r(\mathbf{v})}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D708}(\mathbf{v}):=\frac{c_{1}(\mathbf{v})}{r(\mathbf{v})}\end{eqnarray}$$ satisfying  $\unicode[STIX]{x1D708}(\mathbf{v})\cdot F\geqslant -1$.
$\unicode[STIX]{x1D708}(\mathbf{v})\cdot F\geqslant -1$.
If  $\unicode[STIX]{x1D708}(\mathbf{v})\cdot E\geqslant -1$, then the general sheaf
$\unicode[STIX]{x1D708}(\mathbf{v})\cdot E\geqslant -1$, then the general sheaf  ${\mathcal{V}}\in M(\mathbf{v})$ has at most one nonzero cohomology group and, furthermore,
${\mathcal{V}}\in M(\mathbf{v})$ has at most one nonzero cohomology group and, furthermore,  $H^{2}(\mathbb{F}_{e},{\mathcal{V}})=0$. Conversely, if
$H^{2}(\mathbb{F}_{e},{\mathcal{V}})=0$. Conversely, if  $\unicode[STIX]{x1D712}(\mathbf{v})\geqslant 0$, then the general sheaf in
$\unicode[STIX]{x1D712}(\mathbf{v})\geqslant 0$, then the general sheaf in  $M(\mathbf{v})$ has at most one nonzero cohomology group if and only if
$M(\mathbf{v})$ has at most one nonzero cohomology group if and only if  $\unicode[STIX]{x1D708}(\mathbf{v})\cdot E\geqslant -1$.
$\unicode[STIX]{x1D708}(\mathbf{v})\cdot E\geqslant -1$.
More precisely, we give a simple formula to compute the Betti numbers  $h^{i}(\mathbb{F}_{e},{\mathcal{V}})$ of a general sheaf
$h^{i}(\mathbb{F}_{e},{\mathcal{V}})$ of a general sheaf  ${\mathcal{V}}\in M(\mathbf{v})$; see Theorem 3.1. The statements in Theorem 1.1 contain the most challenging and interesting part of this computation. By replacing
${\mathcal{V}}\in M(\mathbf{v})$; see Theorem 3.1. The statements in Theorem 1.1 contain the most challenging and interesting part of this computation. By replacing  $\mathbf{v}$ by the Serre dual character
$\mathbf{v}$ by the Serre dual character  $\mathbf{v}^{D}$, we can always reduce to the case
$\mathbf{v}^{D}$, we can always reduce to the case  $\unicode[STIX]{x1D708}(\mathbf{v})\cdot F\geqslant -1$, so this assumption is not really restrictive. Under the assumptions of the theorem, the Euler characteristic completely determines the cohomology of the general sheaf if
$\unicode[STIX]{x1D708}(\mathbf{v})\cdot F\geqslant -1$, so this assumption is not really restrictive. Under the assumptions of the theorem, the Euler characteristic completely determines the cohomology of the general sheaf if  $\unicode[STIX]{x1D708}(\mathbf{v})\cdot E\geqslant -1$. If
$\unicode[STIX]{x1D708}(\mathbf{v})\cdot E\geqslant -1$. If  $\unicode[STIX]{x1D708}(\mathbf{v})\cdot E<-1$ and
$\unicode[STIX]{x1D708}(\mathbf{v})\cdot E<-1$ and  $\unicode[STIX]{x1D712}(\mathbf{v})\geqslant 0$, then the general sheaf has both nonzero
$\unicode[STIX]{x1D712}(\mathbf{v})\geqslant 0$, then the general sheaf has both nonzero  $h^{0}$ and
$h^{0}$ and  $h^{1}$. On the other hand, if
$h^{1}$. On the other hand, if  $\unicode[STIX]{x1D708}(\mathbf{v})\cdot E<-1$ and
$\unicode[STIX]{x1D708}(\mathbf{v})\cdot E<-1$ and  $\unicode[STIX]{x1D712}(\mathbf{v})<0$, then general sheaf has only
$\unicode[STIX]{x1D712}(\mathbf{v})<0$, then general sheaf has only  $h^{1}$ provided that the discriminant of
$h^{1}$ provided that the discriminant of  $\mathbf{v}$ is sufficiently large. We quantify this precisely in Corollary 3.9.
$\mathbf{v}$ is sufficiently large. We quantify this precisely in Corollary 3.9.
Theorem 1.1 has many applications. For instance, it shows that effective theta divisors can be constructed on moduli spaces  $M(\mathbf{v})$ if
$M(\mathbf{v})$ if  $\unicode[STIX]{x1D712}(\mathbf{v})=0$,
$\unicode[STIX]{x1D712}(\mathbf{v})=0$,  $\unicode[STIX]{x1D708}(\mathbf{v})\cdot F\geqslant -1$, and
$\unicode[STIX]{x1D708}(\mathbf{v})\cdot F\geqslant -1$, and  $\unicode[STIX]{x1D708}(\mathbf{v})\cdot E\geqslant -1$. In this special case, Theorem 1.1 was shown in [Reference Coskun and HuizengaCH16] by a different approach. The full version of Theorem 1.1 for arbitrary Euler characteristic will also play a crucial role in classifying the stable Chern characters for which the general sheaf in
$\unicode[STIX]{x1D708}(\mathbf{v})\cdot E\geqslant -1$. In this special case, Theorem 1.1 was shown in [Reference Coskun and HuizengaCH16] by a different approach. The full version of Theorem 1.1 for arbitrary Euler characteristic will also play a crucial role in classifying the stable Chern characters for which the general sheaf in  $M(\mathbf{v})$ is globally generated. The next theorem contains the majority of the classification; see Theorems 5.1 and 5.2 for the complete classification.
$M(\mathbf{v})$ is globally generated. The next theorem contains the majority of the classification; see Theorems 5.1 and 5.2 for the complete classification.
Theorem 1.2. Let  $e\geqslant 1$, and let
$e\geqslant 1$, and let  $\mathbf{v}$ be a stable Chern character on
$\mathbf{v}$ be a stable Chern character on  $\mathbb{F}_{e}$. Assume that
$\mathbb{F}_{e}$. Assume that  $r(\mathbf{v})\geqslant 1$,
$r(\mathbf{v})\geqslant 1$,  $\unicode[STIX]{x1D712}(\mathbf{v})\geqslant r(\mathbf{v})+2$,
$\unicode[STIX]{x1D712}(\mathbf{v})\geqslant r(\mathbf{v})+2$,  $\unicode[STIX]{x1D708}(\mathbf{v})\cdot F>0$ and
$\unicode[STIX]{x1D708}(\mathbf{v})\cdot F>0$ and  $\unicode[STIX]{x1D708}(\mathbf{v})\cdot E\geqslant 0$. Then the general sheaf in
$\unicode[STIX]{x1D708}(\mathbf{v})\cdot E\geqslant 0$. Then the general sheaf in  $M(\mathbf{v})$ is globally generated.
$M(\mathbf{v})$ is globally generated.
As a consequence of the  $\mathbb{F}_{1}$ case of Theorem 1.2, we complete an analogous classification for
$\mathbb{F}_{1}$ case of Theorem 1.2, we complete an analogous classification for  $\mathbb{P}^{2}$ started by Bertram et al. [Reference Bertram, Goller and JohnsonBGJ16]. We use two techniques to prove our theorems. We make use of the stack of
$\mathbb{P}^{2}$ started by Bertram et al. [Reference Bertram, Goller and JohnsonBGJ16]. We use two techniques to prove our theorems. We make use of the stack of  $F$-prioritary sheaves, and we find special resolutions of the general sheaf in the spirit of the Gaeta resolution on
$F$-prioritary sheaves, and we find special resolutions of the general sheaf in the spirit of the Gaeta resolution on  $\mathbb{P}^{2}$.
$\mathbb{P}^{2}$.
A torsion-free sheaf  ${\mathcal{V}}$ on
${\mathcal{V}}$ on  $\mathbb{F}_{e}$ is
$\mathbb{F}_{e}$ is  $F$-prioritary if
$F$-prioritary if  $\operatorname{Ext}^{2}({\mathcal{V}},{\mathcal{V}}(-F))=0$. The stack of
$\operatorname{Ext}^{2}({\mathcal{V}},{\mathcal{V}}(-F))=0$. The stack of  $F$-prioritary sheaves
$F$-prioritary sheaves  ${\mathcal{P}}_{F}(\mathbf{v})$ with Chern character
${\mathcal{P}}_{F}(\mathbf{v})$ with Chern character  $\mathbf{v}$ is irreducible [Reference WalterWal98, Proposition 2]. Furthermore,
$\mathbf{v}$ is irreducible [Reference WalterWal98, Proposition 2]. Furthermore,  $\unicode[STIX]{x1D707}_{H}$-semistable sheaves are
$\unicode[STIX]{x1D707}_{H}$-semistable sheaves are  $F$-prioritary, so
$F$-prioritary, so  ${\mathcal{M}}_{H}^{\unicode[STIX]{x1D707}\text{-}\mathit{ss}}(\mathbf{v})\subset {\mathcal{P}}_{F}(\mathbf{v})$ is an open substack, which is dense if it is nonempty. Hence, assuming
${\mathcal{M}}_{H}^{\unicode[STIX]{x1D707}\text{-}\mathit{ss}}(\mathbf{v})\subset {\mathcal{P}}_{F}(\mathbf{v})$ is an open substack, which is dense if it is nonempty. Hence, assuming  $\unicode[STIX]{x1D707}_{H}$-semistable sheaves of character
$\unicode[STIX]{x1D707}_{H}$-semistable sheaves of character  $\mathbf{v}$ exist, to show that the general
$\mathbf{v}$ exist, to show that the general  ${\mathcal{V}}\in M(\mathbf{v})$ satisfies some open property, it suffices to exhibit one
${\mathcal{V}}\in M(\mathbf{v})$ satisfies some open property, it suffices to exhibit one  ${\mathcal{V}}\in {\mathcal{P}}_{F}(\mathbf{v})$ with that property. The advantage of working with
${\mathcal{V}}\in {\mathcal{P}}_{F}(\mathbf{v})$ with that property. The advantage of working with  $F$-prioritary sheaves is that they are much easier to construct than semistable sheaves. For example, one can construct
$F$-prioritary sheaves is that they are much easier to construct than semistable sheaves. For example, one can construct  $F$-prioritary sheaves as certain direct sums of line bundles. We prove Theorem 1.1 by explicitly constructing an
$F$-prioritary sheaves as certain direct sums of line bundles. We prove Theorem 1.1 by explicitly constructing an  $F$-prioritary sheaf with at most one nonzero cohomology group for every character
$F$-prioritary sheaf with at most one nonzero cohomology group for every character  $\mathbf{v}$ satisfying the hypotheses of the Theorem.
$\mathbf{v}$ satisfying the hypotheses of the Theorem.
Remark 1.3. In fact,  $\unicode[STIX]{x1D707}_{H}$-semistability will play essentially no role in this paper. Instead, in the body of the article we state almost all of our theorems for moduli stacks
$\unicode[STIX]{x1D707}_{H}$-semistability will play essentially no role in this paper. Instead, in the body of the article we state almost all of our theorems for moduli stacks  ${\mathcal{P}}_{F}(\mathbf{v})$ where
${\mathcal{P}}_{F}(\mathbf{v})$ where  $\mathbf{v}$ is a character satisfying the Bogomolov inequality
$\mathbf{v}$ is a character satisfying the Bogomolov inequality  $\unicode[STIX]{x1D6E5}(\mathbf{v})\geqslant 0$ (which is automatically satisfied if there is a
$\unicode[STIX]{x1D6E5}(\mathbf{v})\geqslant 0$ (which is automatically satisfied if there is a  $\unicode[STIX]{x1D707}_{H}$-semistable sheaf of character
$\unicode[STIX]{x1D707}_{H}$-semistable sheaf of character  $\mathbf{v}$). When the space
$\mathbf{v}$). When the space  $M(\mathbf{v})$ is nonempty, the analogous results for
$M(\mathbf{v})$ is nonempty, the analogous results for  $M(\mathbf{v})$ follow immediately.
$M(\mathbf{v})$ follow immediately.
Our second technique will be to exploit a convenient resolution of the general sheaf in  $M(\mathbf{v})$. We will be able to read many cohomological properties of the general sheaf from this resolution. Our main result is as follows. See Theorem 4.2 for a stronger statement.
$M(\mathbf{v})$. We will be able to read many cohomological properties of the general sheaf from this resolution. Our main result is as follows. See Theorem 4.2 for a stronger statement.
Theorem 1.4. Suppose  $e\geqslant 2$, and let
$e\geqslant 2$, and let  ${\mathcal{V}}\in M(\mathbf{v})$ be a general
${\mathcal{V}}\in M(\mathbf{v})$ be a general  $\unicode[STIX]{x1D707}_{H}$-semistable sheaf on
$\unicode[STIX]{x1D707}_{H}$-semistable sheaf on  $\mathbb{F}_{e}$. Then there exists a line bundle
$\mathbb{F}_{e}$. Then there exists a line bundle  $L$ such that
$L$ such that  ${\mathcal{V}}$ has a resolution of the form
${\mathcal{V}}$ has a resolution of the form
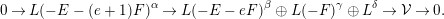 $$\begin{eqnarray}0\rightarrow L(-E-(e+1)F)^{\unicode[STIX]{x1D6FC}}\rightarrow L(-E-eF)^{\unicode[STIX]{x1D6FD}}\oplus L(-F)^{\unicode[STIX]{x1D6FE}}\oplus L^{\unicode[STIX]{x1D6FF}}\rightarrow {\mathcal{V}}\rightarrow 0.\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow L(-E-(e+1)F)^{\unicode[STIX]{x1D6FC}}\rightarrow L(-E-eF)^{\unicode[STIX]{x1D6FD}}\oplus L(-F)^{\unicode[STIX]{x1D6FE}}\oplus L^{\unicode[STIX]{x1D6FF}}\rightarrow {\mathcal{V}}\rightarrow 0.\end{eqnarray}$$We use Theorem 1.4 in order to analyze the most challenging case in the classification of Chern characters such that the general bundle is globally generated. We additionally anticipate resolutions of this type will be useful in studying various questions related to generic vector bundles on Hirzebruch surfaces.
Organization of the paper
In §2, we collect preliminary facts concerning the geometry of Hirzebruch surfaces and moduli of sheaves. In §3, we prove a strengthened version of Theorem 1.1 and compute the Betti numbers of a general sheaf. In §4, we prove a strengthened version of Theorem 1.4. We then classify characters such that the general sheaf is globally generated in §5. We close the paper with some remarks on the open question of determining the Chern characters of ample vector bundles.
2 Preliminaries
In this section, we collect basic facts which we use in the rest of the paper.
2.1 Hirzebruch surfaces
We refer the reader to [Reference BeauvilleBea83], [Reference CoskunCos06] and [Reference HartshorneHart77] for detailed expositions on Hirzebruch surfaces. Let  $e$ be a nonnegative integer and let
$e$ be a nonnegative integer and let  $\mathbb{F}_{e}$ denote the ruled surface
$\mathbb{F}_{e}$ denote the ruled surface  $\mathbb{P}({\mathcal{O}}_{\mathbb{P}^{1}}\oplus {\mathcal{O}}_{\mathbb{P}^{1}}(e))$. Let
$\mathbb{P}({\mathcal{O}}_{\mathbb{P}^{1}}\oplus {\mathcal{O}}_{\mathbb{P}^{1}}(e))$. Let  $\unicode[STIX]{x1D70B}:\mathbb{F}_{e}\rightarrow \mathbb{P}^{1}$ be the natural projection. Let
$\unicode[STIX]{x1D70B}:\mathbb{F}_{e}\rightarrow \mathbb{P}^{1}$ be the natural projection. Let  $F$ be the class of a fiber and let
$F$ be the class of a fiber and let  $E$ be the class of the section of self-intersection
$E$ be the class of the section of self-intersection  $-e$. The intersection pairing on
$-e$. The intersection pairing on  $\mathbb{F}_{e}$ is given by
$\mathbb{F}_{e}$ is given by
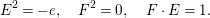 $$\begin{eqnarray}E^{2}=-e,\quad F^{2}=0,\quad F\cdot E=1.\end{eqnarray}$$
$$\begin{eqnarray}E^{2}=-e,\quad F^{2}=0,\quad F\cdot E=1.\end{eqnarray}$$ The effective cone of  $\mathbb{F}_{e}$ is generated by
$\mathbb{F}_{e}$ is generated by  $E$ and
$E$ and  $F$. In fact,
$F$. In fact,
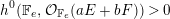 $$\begin{eqnarray}h^{0}(\mathbb{F}_{e},{\mathcal{O}}_{\mathbb{F}_{e}}(aE+bF))>0\end{eqnarray}$$
$$\begin{eqnarray}h^{0}(\mathbb{F}_{e},{\mathcal{O}}_{\mathbb{F}_{e}}(aE+bF))>0\end{eqnarray}$$ if and only if  $a,b\geqslant 0$. Dually, the nef cone of
$a,b\geqslant 0$. Dually, the nef cone of  $\mathbb{F}_{e}$ is generated by
$\mathbb{F}_{e}$ is generated by $E+eF$ and
$E+eF$ and  $F$. The canonical divisor is given by
$F$. The canonical divisor is given by  $K_{\mathbb{F}_{e}}=-2E-(e+2)F$. By Serre duality,
$K_{\mathbb{F}_{e}}=-2E-(e+2)F$. By Serre duality,  $h^{2}(\mathbb{F}_{e},{\mathcal{O}}_{\mathbb{F}_{e}}(aE+bF))>0$ if and only if
$h^{2}(\mathbb{F}_{e},{\mathcal{O}}_{\mathbb{F}_{e}}(aE+bF))>0$ if and only if  $a\leqslant -2$ and
$a\leqslant -2$ and $b\leqslant -e-2$. The following theorem summarizes the cohomology of line bundles on
$b\leqslant -e-2$. The following theorem summarizes the cohomology of line bundles on  $\mathbb{F}_{e}$ (also see [Reference CoskunCos06, Reference Coskun and HuizengaCH16, Reference HartshorneHart77]).
$\mathbb{F}_{e}$ (also see [Reference CoskunCos06, Reference Coskun and HuizengaCH16, Reference HartshorneHart77]).
Theorem 2.1. Let  $L={\mathcal{O}}_{\mathbb{F}_{e}}(aE+bF)$ be a line bundle on
$L={\mathcal{O}}_{\mathbb{F}_{e}}(aE+bF)$ be a line bundle on  $\mathbb{F}_{e}$. Then
$\mathbb{F}_{e}$. Then
(1) We have
 $$\begin{eqnarray}\unicode[STIX]{x1D712}(L)=(a+1)(b+1)-e\frac{a(a+1)}{2}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D712}(L)=(a+1)(b+1)-e\frac{a(a+1)}{2}.\end{eqnarray}$$(2) If
 $L\cdot F\geqslant -1$, then
$L\cdot F\geqslant -1$, then  $h^{2}(\mathbb{F}_{e},L)=0$.
$h^{2}(\mathbb{F}_{e},L)=0$.(3) If
 $L\cdot F\leqslant -1$, then
$L\cdot F\leqslant -1$, then  $h^{0}(\mathbb{F}_{e},L)=0$.
$h^{0}(\mathbb{F}_{e},L)=0$.(4) In particular, if
 $L\cdot F=-1$, then
$L\cdot F=-1$, then  $L$ has no cohomology in any degree.
$L$ has no cohomology in any degree.Now suppose
 $L\cdot F>-1$. Then
$L\cdot F>-1$. Then  $h^{2}(\mathbb{F}_{e},L)=0$, so either of the numbers
$h^{2}(\mathbb{F}_{e},L)=0$, so either of the numbers  $h^{0}(\mathbb{F}_{e},L)$ or
$h^{0}(\mathbb{F}_{e},L)$ or  $h^{1}(\mathbb{F}_{e},L)$ determine the cohomology of
$h^{1}(\mathbb{F}_{e},L)$ determine the cohomology of  $L$. These can be determined as follows.
$L$. These can be determined as follows.(5) If
 $L\cdot E\geqslant -1$, then
$L\cdot E\geqslant -1$, then  $H^{1}(\mathbb{F}_{e},L)=0$, and so
$H^{1}(\mathbb{F}_{e},L)=0$, and so  $h^{0}(\mathbb{F}_{e},L)=\unicode[STIX]{x1D712}(L)$.
$h^{0}(\mathbb{F}_{e},L)=\unicode[STIX]{x1D712}(L)$.(6) If
 $L\cdot E<-1$, then
$L\cdot E<-1$, then  $H^{0}(\mathbb{F}_{e},L)\cong H^{0}(\mathbb{F}_{e},L(-E))$, and so the cohomology of
$H^{0}(\mathbb{F}_{e},L)\cong H^{0}(\mathbb{F}_{e},L(-E))$, and so the cohomology of  $L$ can be determined inductively using (3) and (5).
$L$ can be determined inductively using (3) and (5).
(If  $L\cdot F<-1$ then the cohomology of
$L\cdot F<-1$ then the cohomology of  $L$ can be determined by Serre duality.)
$L$ can be determined by Serre duality.)
While the proof is well known, we include it since the argument is relevant to our approach for vector bundles.
Proof. Part (1) is just Riemann–Roch. Part (3) comes from the description of the effective cone, and (2) follows by Serre duality. Part (4) is just a combination of (1)–(3).
(5) Suppose  $a=L\cdot F\geqslant 0$ and
$a=L\cdot F\geqslant 0$ and  $L\cdot E\geqslant -1$, and consider the restriction sequence
$L\cdot E\geqslant -1$, and consider the restriction sequence
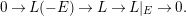 $$\begin{eqnarray}0\rightarrow L(-E)\rightarrow L\rightarrow L|_{E}\rightarrow 0.\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow L(-E)\rightarrow L\rightarrow L|_{E}\rightarrow 0.\end{eqnarray}$$ Then  $H^{1}(E,L|_{E})=0$, so
$H^{1}(E,L|_{E})=0$, so  $H^{1}(\mathbb{F}_{e},L)$ is a quotient of
$H^{1}(\mathbb{F}_{e},L)$ is a quotient of  $H^{1}(\mathbb{F}_{e},L(-E))$. Repeating this process, we eventually find that
$H^{1}(\mathbb{F}_{e},L(-E))$. Repeating this process, we eventually find that  $H^{1}(\mathbb{F}_{e},L)$ is a quotient of
$H^{1}(\mathbb{F}_{e},L)$ is a quotient of  $H^{1}(\mathbb{F}_{e},L(-(a+1)E))=H^{1}(\mathbb{F}_{e},{\mathcal{O}}_{\mathbb{F}_{e}}(-E+bF))=0$ by (4). Therefore,
$H^{1}(\mathbb{F}_{e},L(-(a+1)E))=H^{1}(\mathbb{F}_{e},{\mathcal{O}}_{\mathbb{F}_{e}}(-E+bF))=0$ by (4). Therefore,  $H^{1}(\mathbb{F}_{e},L)=0$.
$H^{1}(\mathbb{F}_{e},L)=0$.
(6) The isomorphism  $H^{0}(\mathbb{F}_{e},L)\cong H^{0}(\mathbb{F}_{e},L(-E))$ comes immediately from the restriction sequence. When we twist
$H^{0}(\mathbb{F}_{e},L)\cong H^{0}(\mathbb{F}_{e},L(-E))$ comes immediately from the restriction sequence. When we twist  $L$ by
$L$ by  $-E$, the intersection number with
$-E$, the intersection number with  $E$ increases by
$E$ increases by  $e$ and the intersection number with
$e$ and the intersection number with  $F$ decreases by
$F$ decreases by  $1$. Thus there is some smallest integer
$1$. Thus there is some smallest integer  $m>0$ such that either
$m>0$ such that either  $L(-mE)\cdot F\leqslant -1$ or
$L(-mE)\cdot F\leqslant -1$ or  $L(-mE)\cdot E\geqslant -1$, and by induction
$L(-mE)\cdot E\geqslant -1$, and by induction  $h^{0}(\mathbb{F}_{e},L)=h^{0}(\mathbb{F}_{e},L(-mE))$. If
$h^{0}(\mathbb{F}_{e},L)=h^{0}(\mathbb{F}_{e},L(-mE))$. If  $L(-mE)\cdot F\leqslant -1$, we have
$L(-mE)\cdot F\leqslant -1$, we have  $h^{0}(\mathbb{F}_{e},L)=0$ by (3). On the other hand, if
$h^{0}(\mathbb{F}_{e},L)=0$ by (3). On the other hand, if  $L(-mE)\cdot F>-1$ and
$L(-mE)\cdot F>-1$ and  $L(-mE)\cdot E\geqslant -1$, then we have
$L(-mE)\cdot E\geqslant -1$, then we have  $h^{0}(\mathbb{F}_{e},L)=\unicode[STIX]{x1D712}(L(-mE))$ by (5).◻
$h^{0}(\mathbb{F}_{e},L)=\unicode[STIX]{x1D712}(L(-mE))$ by (5).◻
Remark 2.2. In particular, the line bundles
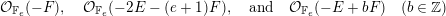 $$\begin{eqnarray}{\mathcal{O}}_{\mathbb{F}_{e}}(-F),\quad {\mathcal{O}}_{\mathbb{F}_{e}}(-2E-(e+1)F),\quad \text{and}\quad {\mathcal{O}}_{\mathbb{F}_{e}}(-E+bF)\quad (b\in \mathbb{Z})\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{O}}_{\mathbb{F}_{e}}(-F),\quad {\mathcal{O}}_{\mathbb{F}_{e}}(-2E-(e+1)F),\quad \text{and}\quad {\mathcal{O}}_{\mathbb{F}_{e}}(-E+bF)\quad (b\in \mathbb{Z})\end{eqnarray}$$all have no cohomology in any degree.
2.2 Numerical invariants and semistability
We refer the reader to [Reference Coskun and HuizengaCH15, Reference Huybrechts and LehnHuL10, Reference Le PotierLeP97] for more details on moduli spaces of vector bundles on surfaces. Let  $X$ be a surface and let
$X$ be a surface and let  $H$ be an ample divisor on
$H$ be an ample divisor on  $X$. For a sheaf
$X$. For a sheaf  ${\mathcal{V}}$ (or Chern character
${\mathcal{V}}$ (or Chern character  $\mathbf{v}$) of positive rank we respectively define the
$\mathbf{v}$) of positive rank we respectively define the  $H$-slope, total slope, and discriminant:
$H$-slope, total slope, and discriminant:
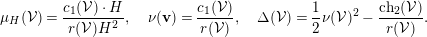 $$\begin{eqnarray}\unicode[STIX]{x1D707}_{H}({\mathcal{V}})=\frac{c_{1}({\mathcal{V}})\cdot H}{r({\mathcal{V}})H^{2}},\quad \unicode[STIX]{x1D708}(\mathbf{v})=\frac{c_{1}({\mathcal{V}})}{r({\mathcal{V}})},\quad \unicode[STIX]{x1D6E5}({\mathcal{V}})=\frac{1}{2}\unicode[STIX]{x1D708}({\mathcal{V}})^{2}-\frac{\operatorname{ch}_{2}({\mathcal{V}})}{r({\mathcal{V}})}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D707}_{H}({\mathcal{V}})=\frac{c_{1}({\mathcal{V}})\cdot H}{r({\mathcal{V}})H^{2}},\quad \unicode[STIX]{x1D708}(\mathbf{v})=\frac{c_{1}({\mathcal{V}})}{r({\mathcal{V}})},\quad \unicode[STIX]{x1D6E5}({\mathcal{V}})=\frac{1}{2}\unicode[STIX]{x1D708}({\mathcal{V}})^{2}-\frac{\operatorname{ch}_{2}({\mathcal{V}})}{r({\mathcal{V}})}.\end{eqnarray}$$The discriminant has the following important properties:
(1) If
 $L$ is a line bundle then
$L$ is a line bundle then  $\unicode[STIX]{x1D6E5}(L)=0$.
$\unicode[STIX]{x1D6E5}(L)=0$.(2) If
 ${\mathcal{V}}$ is torsion-free and
${\mathcal{V}}$ is torsion-free and  ${\mathcal{W}}$ is a nonzero vector bundle, then
${\mathcal{W}}$ is a nonzero vector bundle, then  $\unicode[STIX]{x1D6E5}({\mathcal{V}}\otimes {\mathcal{W}})=\unicode[STIX]{x1D6E5}({\mathcal{V}})+\unicode[STIX]{x1D6E5}({\mathcal{W}})$. In particular,
$\unicode[STIX]{x1D6E5}({\mathcal{V}}\otimes {\mathcal{W}})=\unicode[STIX]{x1D6E5}({\mathcal{V}})+\unicode[STIX]{x1D6E5}({\mathcal{W}})$. In particular,  $\unicode[STIX]{x1D6E5}({\mathcal{V}}\otimes L)=\unicode[STIX]{x1D6E5}({\mathcal{V}})$ for any line bundle
$\unicode[STIX]{x1D6E5}({\mathcal{V}}\otimes L)=\unicode[STIX]{x1D6E5}({\mathcal{V}})$ for any line bundle  $L$.
$L$.
If we put  $P(\unicode[STIX]{x1D708})=\unicode[STIX]{x1D712}({\mathcal{O}}_{X})+{\textstyle \frac{1}{2}}\unicode[STIX]{x1D708}\cdot (\unicode[STIX]{x1D708}-K_{X})$, then the Riemann–Roch formula reads
$P(\unicode[STIX]{x1D708})=\unicode[STIX]{x1D712}({\mathcal{O}}_{X})+{\textstyle \frac{1}{2}}\unicode[STIX]{x1D708}\cdot (\unicode[STIX]{x1D708}-K_{X})$, then the Riemann–Roch formula reads
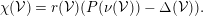 $$\begin{eqnarray}\unicode[STIX]{x1D712}({\mathcal{V}})=r({\mathcal{V}})(P(\unicode[STIX]{x1D708}({\mathcal{V}}))-\unicode[STIX]{x1D6E5}({\mathcal{V}})).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D712}({\mathcal{V}})=r({\mathcal{V}})(P(\unicode[STIX]{x1D708}({\mathcal{V}}))-\unicode[STIX]{x1D6E5}({\mathcal{V}})).\end{eqnarray}$$ In the special case of  $\mathbb{F}_{e}$, if
$\mathbb{F}_{e}$, if  ${\mathcal{V}}$ has rank
${\mathcal{V}}$ has rank  $r$ and total slope
$r$ and total slope  $\unicode[STIX]{x1D708}({\mathcal{V}})=(k/r)E+(l/r)F$, then the term
$\unicode[STIX]{x1D708}({\mathcal{V}})=(k/r)E+(l/r)F$, then the term  $P(\unicode[STIX]{x1D708}({\mathcal{V}}))$ becomes
$P(\unicode[STIX]{x1D708}({\mathcal{V}}))$ becomes
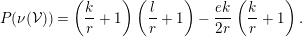 $$\begin{eqnarray}P(\unicode[STIX]{x1D708}({\mathcal{V}}))=\left(\frac{k}{r}+1\right)\left(\frac{l}{r}+1\right)-\frac{ek}{2r}\left(\frac{k}{r}+1\right).\end{eqnarray}$$
$$\begin{eqnarray}P(\unicode[STIX]{x1D708}({\mathcal{V}}))=\left(\frac{k}{r}+1\right)\left(\frac{l}{r}+1\right)-\frac{ek}{2r}\left(\frac{k}{r}+1\right).\end{eqnarray}$$We find the following easy consequence of Hirzebruch–Riemann–Roch useful.
Lemma 2.3. Let  $X$ be a smooth projective surface with canonical class
$X$ be a smooth projective surface with canonical class  $K_{X}$. Let
$K_{X}$. Let  ${\mathcal{V}}$ be a torsion-free sheaf of rank
${\mathcal{V}}$ be a torsion-free sheaf of rank  $r$ on
$r$ on  $X$ and let
$X$ and let  $L$ be a line bundle on
$L$ be a line bundle on  $X$. Then
$X$. Then
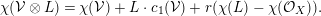 $$\begin{eqnarray}\unicode[STIX]{x1D712}({\mathcal{V}}\otimes L)=\unicode[STIX]{x1D712}({\mathcal{V}})+L\cdot c_{1}({\mathcal{V}})+r(\unicode[STIX]{x1D712}(L)-\unicode[STIX]{x1D712}({\mathcal{O}}_{X})).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D712}({\mathcal{V}}\otimes L)=\unicode[STIX]{x1D712}({\mathcal{V}})+L\cdot c_{1}({\mathcal{V}})+r(\unicode[STIX]{x1D712}(L)-\unicode[STIX]{x1D712}({\mathcal{O}}_{X})).\end{eqnarray}$$ A torsion-free sheaf  ${\mathcal{V}}$ on
${\mathcal{V}}$ on  $X$ is
$X$ is  $\unicode[STIX]{x1D707}_{H}$-semistable if whenever
$\unicode[STIX]{x1D707}_{H}$-semistable if whenever  ${\mathcal{W}}\subset {\mathcal{V}}$ is a nonzero subsheaf we have
${\mathcal{W}}\subset {\mathcal{V}}$ is a nonzero subsheaf we have  $\unicode[STIX]{x1D707}_{H}({\mathcal{W}})\leqslant \unicode[STIX]{x1D707}_{H}({\mathcal{V}})$. Ordinary
$\unicode[STIX]{x1D707}_{H}({\mathcal{W}})\leqslant \unicode[STIX]{x1D707}_{H}({\mathcal{V}})$. Ordinary  $H$-Gieseker semistability implies
$H$-Gieseker semistability implies  $\unicode[STIX]{x1D707}_{H}$-semistability, but all the theorems in this paper will hold for the weaker
$\unicode[STIX]{x1D707}_{H}$-semistability, but all the theorems in this paper will hold for the weaker  $\unicode[STIX]{x1D707}_{H}$-semistability. The Bogomolov inequality implies that
$\unicode[STIX]{x1D707}_{H}$-semistability. The Bogomolov inequality implies that  $\unicode[STIX]{x1D6E5}({\mathcal{V}})\geqslant 0$ for any
$\unicode[STIX]{x1D6E5}({\mathcal{V}})\geqslant 0$ for any  $\unicode[STIX]{x1D707}_{H}$-semistable sheaf.
$\unicode[STIX]{x1D707}_{H}$-semistable sheaf.
2.3 Prioritary sheaves
While our results are perhaps the most interesting in the context of semistable sheaves, stronger results can be proved by working with the easier notion of prioritary sheaves.
Definition 2.4. Let  $D$ be a divisor on a smooth surface
$D$ be a divisor on a smooth surface  $X$. A torsion-free sheaf
$X$. A torsion-free sheaf  ${\mathcal{V}}$ is called
${\mathcal{V}}$ is called  $D$-prioritary if
$D$-prioritary if  $\operatorname{Ext}^{2}({\mathcal{V}},{\mathcal{V}}(-D))=0$.
$\operatorname{Ext}^{2}({\mathcal{V}},{\mathcal{V}}(-D))=0$.
We write  ${\mathcal{P}}_{D}(\mathbf{v})$ (or
${\mathcal{P}}_{D}(\mathbf{v})$ (or  ${\mathcal{P}}_{X,D}(\mathbf{v})$ if
${\mathcal{P}}_{X,D}(\mathbf{v})$ if  $X$ is not clear) for the stack of
$X$ is not clear) for the stack of  $D$-prioritary sheaves on
$D$-prioritary sheaves on  $X$.
$X$.
In this paper, we primarily consider  $F$-prioritary sheaves on
$F$-prioritary sheaves on  $\mathbb{F}_{e}$, where
$\mathbb{F}_{e}$, where  $F$ is the class of a fiber. If
$F$ is the class of a fiber. If  $H$ is any ample class on
$H$ is any ample class on  $\mathbb{F}_{e}$ and
$\mathbb{F}_{e}$ and  ${\mathcal{V}}$ is a torsion-free
${\mathcal{V}}$ is a torsion-free  $\unicode[STIX]{x1D707}_{H}$-semistable sheaf, then
$\unicode[STIX]{x1D707}_{H}$-semistable sheaf, then  ${\mathcal{V}}$ is automatically
${\mathcal{V}}$ is automatically  $F$-prioritary. Indeed, suppose
$F$-prioritary. Indeed, suppose  ${\mathcal{V}}$ is
${\mathcal{V}}$ is  $\unicode[STIX]{x1D707}_{H}$-semistable. By Serre duality
$\unicode[STIX]{x1D707}_{H}$-semistable. By Serre duality
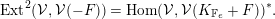 $$\begin{eqnarray}\operatorname{Ext}^{2}({\mathcal{V}},{\mathcal{V}}(-F))=\operatorname{Hom}({\mathcal{V}},{\mathcal{V}}(K_{\mathbb{ F}_{e}}+F))^{\ast }.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Ext}^{2}({\mathcal{V}},{\mathcal{V}}(-F))=\operatorname{Hom}({\mathcal{V}},{\mathcal{V}}(K_{\mathbb{ F}_{e}}+F))^{\ast }.\end{eqnarray}$$ Since  $K_{\mathbb{F}_{e}}+F$ is anti-effective, we have
$K_{\mathbb{F}_{e}}+F$ is anti-effective, we have  $(K_{\mathbb{F}_{e}}+F)\cdot H<0$. Therefore,
$(K_{\mathbb{F}_{e}}+F)\cdot H<0$. Therefore,  $\unicode[STIX]{x1D707}_{H}({\mathcal{V}})>\unicode[STIX]{x1D707}_{H}({\mathcal{V}}(K_{\mathbb{F}_{e}}+F))$, and
$\unicode[STIX]{x1D707}_{H}({\mathcal{V}})>\unicode[STIX]{x1D707}_{H}({\mathcal{V}}(K_{\mathbb{F}_{e}}+F))$, and  $\operatorname{Hom}({\mathcal{V}},{\mathcal{V}}(K_{\mathbb{F}_{e}}+F))=0$ by
$\operatorname{Hom}({\mathcal{V}},{\mathcal{V}}(K_{\mathbb{F}_{e}}+F))=0$ by  $\unicode[STIX]{x1D707}_{H}$-semistability. Therefore,
$\unicode[STIX]{x1D707}_{H}$-semistability. Therefore,  ${\mathcal{V}}$ is
${\mathcal{V}}$ is  $F$-prioritary. It follows from openness of stability that the stack
$F$-prioritary. It follows from openness of stability that the stack  ${\mathcal{M}}_{H}^{\unicode[STIX]{x1D707}\text{-}\mathit{ss}}(\mathbf{v})$ is an open substack of
${\mathcal{M}}_{H}^{\unicode[STIX]{x1D707}\text{-}\mathit{ss}}(\mathbf{v})$ is an open substack of  ${\mathcal{P}}_{F}(\mathbf{v})$. Furthermore, if there are
${\mathcal{P}}_{F}(\mathbf{v})$. Furthermore, if there are  $\unicode[STIX]{x1D707}_{H}$-semistable sheaves of character
$\unicode[STIX]{x1D707}_{H}$-semistable sheaves of character  $\mathbf{v}$, then it is dense by the following theorem of Walter [Reference WalterWal98].
$\mathbf{v}$, then it is dense by the following theorem of Walter [Reference WalterWal98].
Theorem 2.5. Let  $\unicode[STIX]{x1D70B}:X\rightarrow \mathbb{P}^{1}$ be a geometrically ruled surface with fiber class
$\unicode[STIX]{x1D70B}:X\rightarrow \mathbb{P}^{1}$ be a geometrically ruled surface with fiber class  $F$, and let
$F$, and let  $\mathbf{v}\in K(X)$ have positive rank. Then the stack
$\mathbf{v}\in K(X)$ have positive rank. Then the stack  ${\mathcal{P}}_{F}(\mathbf{v})$ is irreducible. Furthermore, if
${\mathcal{P}}_{F}(\mathbf{v})$ is irreducible. Furthermore, if  $r(\mathbf{v})\geqslant 2$ and
$r(\mathbf{v})\geqslant 2$ and  ${\mathcal{P}}_{F}(\mathbf{v})$ is nonempty, then a general
${\mathcal{P}}_{F}(\mathbf{v})$ is nonempty, then a general  ${\mathcal{V}}\in {\mathcal{P}}_{F}(\mathbf{v})$ is a vector bundle.
${\mathcal{V}}\in {\mathcal{P}}_{F}(\mathbf{v})$ is a vector bundle.
In particular, to show that a general  $\unicode[STIX]{x1D707}_{H}$-semistable sheaf on
$\unicode[STIX]{x1D707}_{H}$-semistable sheaf on  $\mathbb{F}_{e}$ of character
$\mathbb{F}_{e}$ of character  $\mathbf{v}$ satisfies some open property, it is sufficient to produce an
$\mathbf{v}$ satisfies some open property, it is sufficient to produce an  $F$-prioritary sheaf with that property.
$F$-prioritary sheaf with that property.
Every vector bundle on a rational curve is a direct sum of line bundles  $\bigoplus _{i=1}^{r}{\mathcal{O}}_{\mathbb{P}^{1}}(a_{i})$. The vector bundle is balanced if
$\bigoplus _{i=1}^{r}{\mathcal{O}}_{\mathbb{P}^{1}}(a_{i})$. The vector bundle is balanced if  $|a_{i}-a_{j}|\leqslant 1$ for all
$|a_{i}-a_{j}|\leqslant 1$ for all  $i,j$. The next proposition explains the importance of the prioritary condition.
$i,j$. The next proposition explains the importance of the prioritary condition.
Proposition 2.6. Let  $C$ be a curve on a surface
$C$ be a curve on a surface  $X$ and let
$X$ and let  ${\mathcal{F}}_{s}/S$ be a complete family of
${\mathcal{F}}_{s}/S$ be a complete family of  $C$-prioritary sheaves which are locally free on
$C$-prioritary sheaves which are locally free on  $C$. Then the restricted family
$C$. Then the restricted family  ${\mathcal{F}}_{s}|_{C}/S$ is complete.
${\mathcal{F}}_{s}|_{C}/S$ is complete.
Therefore, if  $C$ is a rational curve, then
$C$ is a rational curve, then  ${\mathcal{F}}_{s}|_{C}$ is balanced for all
${\mathcal{F}}_{s}|_{C}$ is balanced for all  $s$ in an open dense subset of
$s$ in an open dense subset of  $S$.
$S$.
Proof. The Kodaira–Spencer map of the restricted family
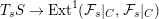 $$\begin{eqnarray}T_{s}S\rightarrow \operatorname{Ext}^{1}({\mathcal{F}}_{s}|_{C},{\mathcal{F}}_{s}|_{C})\end{eqnarray}$$
$$\begin{eqnarray}T_{s}S\rightarrow \operatorname{Ext}^{1}({\mathcal{F}}_{s}|_{C},{\mathcal{F}}_{s}|_{C})\end{eqnarray}$$factors as a composition
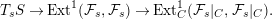 $$\begin{eqnarray}T_{s}S\rightarrow \operatorname{Ext}^{1}({\mathcal{F}}_{s},{\mathcal{F}}_{s})\rightarrow \operatorname{Ext}_{C}^{1}({\mathcal{F}}_{s}|_{C},{\mathcal{F}}_{s}|_{C}).\end{eqnarray}$$
$$\begin{eqnarray}T_{s}S\rightarrow \operatorname{Ext}^{1}({\mathcal{F}}_{s},{\mathcal{F}}_{s})\rightarrow \operatorname{Ext}_{C}^{1}({\mathcal{F}}_{s}|_{C},{\mathcal{F}}_{s}|_{C}).\end{eqnarray}$$ The first map is surjective since the family  ${\mathcal{F}}$ is a complete family. We have an identification
${\mathcal{F}}$ is a complete family. We have an identification
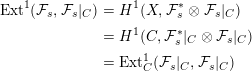 $$\begin{eqnarray}\displaystyle \operatorname{Ext}^{1}({\mathcal{F}}_{s},{\mathcal{F}}_{s}|_{C}) & = & \displaystyle H^{1}(X,{\mathcal{F}}_{s}^{\ast }\otimes {\mathcal{F}}_{s}|_{C})\nonumber\\ \displaystyle & = & \displaystyle H^{1}(C,{\mathcal{F}}_{s}^{\ast }|_{C}\otimes {\mathcal{F}}_{s}|_{C})\nonumber\\ \displaystyle & = & \displaystyle \operatorname{Ext}_{C}^{1}({\mathcal{F}}_{s}|_{C},{\mathcal{F}}_{s}|_{C})\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \operatorname{Ext}^{1}({\mathcal{F}}_{s},{\mathcal{F}}_{s}|_{C}) & = & \displaystyle H^{1}(X,{\mathcal{F}}_{s}^{\ast }\otimes {\mathcal{F}}_{s}|_{C})\nonumber\\ \displaystyle & = & \displaystyle H^{1}(C,{\mathcal{F}}_{s}^{\ast }|_{C}\otimes {\mathcal{F}}_{s}|_{C})\nonumber\\ \displaystyle & = & \displaystyle \operatorname{Ext}_{C}^{1}({\mathcal{F}}_{s}|_{C},{\mathcal{F}}_{s}|_{C})\nonumber\end{eqnarray}$$ since  ${\mathcal{F}}_{s}$ is locally free along C. Hence, the second map in the factorization appears in the long exact sequence obtained by applying
${\mathcal{F}}_{s}$ is locally free along C. Hence, the second map in the factorization appears in the long exact sequence obtained by applying  $\operatorname{Hom}({\mathcal{F}}_{s},{\mathcal{F}}_{s}\otimes -)$ to
$\operatorname{Hom}({\mathcal{F}}_{s},{\mathcal{F}}_{s}\otimes -)$ to
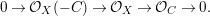 $$\begin{eqnarray}0\rightarrow {\mathcal{O}}_{X}(-C)\rightarrow {\mathcal{O}}_{X}\rightarrow {\mathcal{O}}_{C}\rightarrow 0.\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow {\mathcal{O}}_{X}(-C)\rightarrow {\mathcal{O}}_{X}\rightarrow {\mathcal{O}}_{C}\rightarrow 0.\end{eqnarray}$$By the long exact sequence of cohomology
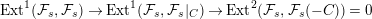 $$\begin{eqnarray}\operatorname{Ext}^{1}({\mathcal{F}}_{s},{\mathcal{F}}_{s})\rightarrow \operatorname{Ext}^{1}({\mathcal{F}}_{s},{\mathcal{F}}_{s}|_{C})\rightarrow \operatorname{Ext}^{2}({\mathcal{F}}_{s},{\mathcal{F}}_{s}(-C))=0\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Ext}^{1}({\mathcal{F}}_{s},{\mathcal{F}}_{s})\rightarrow \operatorname{Ext}^{1}({\mathcal{F}}_{s},{\mathcal{F}}_{s}|_{C})\rightarrow \operatorname{Ext}^{2}({\mathcal{F}}_{s},{\mathcal{F}}_{s}(-C))=0\end{eqnarray}$$ we conclude that the Kodaira–Spencer map is surjective, and  ${\mathcal{F}}_{s}|_{C}/S$ is complete.
${\mathcal{F}}_{s}|_{C}/S$ is complete.
In any complete family of vector bundles on  $\mathbb{P}^{1}$ parameterized by an irreducible base, the general bundle is balanced. The second statement follows.◻
$\mathbb{P}^{1}$ parameterized by an irreducible base, the general bundle is balanced. The second statement follows.◻
One advantage of working with prioritary sheaves is that they are well behaved under elementary modifications. The following result is well known but we include the proof for completeness and lack of a single streamlined reference.
Lemma 2.7. Let  $L$ be a line bundle on a smooth surface
$L$ be a line bundle on a smooth surface  $X$. Let
$X$. Let  ${\mathcal{V}}$ be a torsion-free sheaf on
${\mathcal{V}}$ be a torsion-free sheaf on  $X$, and let
$X$, and let  ${\mathcal{V}}^{\prime }$ be a general elementary modification of
${\mathcal{V}}^{\prime }$ be a general elementary modification of  ${\mathcal{V}}$ at a general point
${\mathcal{V}}$ at a general point  $p\in X$, defined as the kernel of a general surjection
$p\in X$, defined as the kernel of a general surjection  $\unicode[STIX]{x1D719}:{\mathcal{V}}\rightarrow {\mathcal{O}}_{p}$:
$\unicode[STIX]{x1D719}:{\mathcal{V}}\rightarrow {\mathcal{O}}_{p}$:
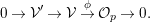 $$\begin{eqnarray}0\rightarrow {\mathcal{V}}^{\prime }\rightarrow {\mathcal{V}}\stackrel{\unicode[STIX]{x1D719}}{\rightarrow }{\mathcal{O}}_{p}\rightarrow 0.\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow {\mathcal{V}}^{\prime }\rightarrow {\mathcal{V}}\stackrel{\unicode[STIX]{x1D719}}{\rightarrow }{\mathcal{O}}_{p}\rightarrow 0.\end{eqnarray}$$(1) If
 ${\mathcal{V}}$ is
${\mathcal{V}}$ is  $L$-prioritary, then
$L$-prioritary, then  ${\mathcal{V}}^{\prime }$ is
${\mathcal{V}}^{\prime }$ is  $L$-prioritary.
$L$-prioritary.(2) The sheaves
 ${\mathcal{V}}$ and
${\mathcal{V}}$ and  ${\mathcal{V}}^{\prime }$ have the same rank and
${\mathcal{V}}^{\prime }$ have the same rank and  $c_{1}$, and
$c_{1}$, and  $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D712}({\mathcal{V}}^{\prime }) & = & \displaystyle \unicode[STIX]{x1D712}({\mathcal{V}})-1\nonumber\\ \displaystyle \unicode[STIX]{x1D6E5}({\mathcal{V}}^{\prime }) & = & \displaystyle \unicode[STIX]{x1D6E5}({\mathcal{V}})+\frac{1}{r}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D712}({\mathcal{V}}^{\prime }) & = & \displaystyle \unicode[STIX]{x1D712}({\mathcal{V}})-1\nonumber\\ \displaystyle \unicode[STIX]{x1D6E5}({\mathcal{V}}^{\prime }) & = & \displaystyle \unicode[STIX]{x1D6E5}({\mathcal{V}})+\frac{1}{r}.\nonumber\end{eqnarray}$$(3) We have
 $H^{2}(X,{\mathcal{V}})\cong H^{2}(X,{\mathcal{V}}^{\prime })$.
$H^{2}(X,{\mathcal{V}})\cong H^{2}(X,{\mathcal{V}}^{\prime })$.(4) If at least one of
 $H^{0}(X,{\mathcal{V}})$ or
$H^{0}(X,{\mathcal{V}})$ or  $H^{1}(X,{\mathcal{V}})$ is zero, then at least one of
$H^{1}(X,{\mathcal{V}})$ is zero, then at least one of  $H^{0}(X,{\mathcal{V}}^{\prime })$ or
$H^{0}(X,{\mathcal{V}}^{\prime })$ or  $H^{1}(X,{\mathcal{V}}^{\prime })$ is zero. In particular, if
$H^{1}(X,{\mathcal{V}}^{\prime })$ is zero. In particular, if  $H^{2}(X,{\mathcal{V}})=0$ and
$H^{2}(X,{\mathcal{V}})=0$ and  ${\mathcal{V}}$ has at most one nonzero cohomology group, then
${\mathcal{V}}$ has at most one nonzero cohomology group, then  $H^{2}(X,{\mathcal{V}}^{\prime })=0$ and
$H^{2}(X,{\mathcal{V}}^{\prime })=0$ and  ${\mathcal{V}}^{\prime }$ has at most one nonzero cohomology group.
${\mathcal{V}}^{\prime }$ has at most one nonzero cohomology group.
Proof. (1) Clearly  ${\mathcal{V}}^{\prime }$ is torsion-free since
${\mathcal{V}}^{\prime }$ is torsion-free since  ${\mathcal{V}}$ is. We have
${\mathcal{V}}$ is. We have  $\operatorname{Ext}^{2}({\mathcal{V}},{\mathcal{V}}(-L))=0$ since
$\operatorname{Ext}^{2}({\mathcal{V}},{\mathcal{V}}(-L))=0$ since  ${\mathcal{V}}$ is
${\mathcal{V}}$ is  $L$-prioritary. We would like to show that
$L$-prioritary. We would like to show that  $\operatorname{Ext}^{2}({\mathcal{V}}^{\prime },{\mathcal{V}}^{\prime }(-L))=0$. Applying
$\operatorname{Ext}^{2}({\mathcal{V}}^{\prime },{\mathcal{V}}^{\prime }(-L))=0$. Applying  $\operatorname{Ext}(-,{\mathcal{V}}^{\prime }(-L))$ to the sequence, we obtain a surjection
$\operatorname{Ext}(-,{\mathcal{V}}^{\prime }(-L))$ to the sequence, we obtain a surjection
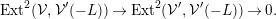 $$\begin{eqnarray}\operatorname{Ext}^{2}({\mathcal{V}},{\mathcal{V}}^{\prime }(-L))\rightarrow \operatorname{Ext}^{2}({\mathcal{V}}^{\prime },{\mathcal{V}}^{\prime }(-L))\rightarrow 0.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Ext}^{2}({\mathcal{V}},{\mathcal{V}}^{\prime }(-L))\rightarrow \operatorname{Ext}^{2}({\mathcal{V}}^{\prime },{\mathcal{V}}^{\prime }(-L))\rightarrow 0.\end{eqnarray}$$ Hence, it suffices to show that  $\operatorname{Ext}^{2}({\mathcal{V}},{\mathcal{V}}^{\prime }(-L))=0$. Applying
$\operatorname{Ext}^{2}({\mathcal{V}},{\mathcal{V}}^{\prime }(-L))=0$. Applying  $\operatorname{Ext}({\mathcal{V}},-)$ to the sequence twisted by
$\operatorname{Ext}({\mathcal{V}},-)$ to the sequence twisted by  $-L$, we obtain
$-L$, we obtain
 $$\begin{eqnarray}\operatorname{Ext}^{1}({\mathcal{V}},{\mathcal{O}}_{p})\rightarrow \operatorname{Ext}^{2}({\mathcal{V}},{\mathcal{V}}^{\prime }(-L))\rightarrow \operatorname{Ext}^{2}({\mathcal{V}},{\mathcal{V}}(-L)).\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Ext}^{1}({\mathcal{V}},{\mathcal{O}}_{p})\rightarrow \operatorname{Ext}^{2}({\mathcal{V}},{\mathcal{V}}^{\prime }(-L))\rightarrow \operatorname{Ext}^{2}({\mathcal{V}},{\mathcal{V}}(-L)).\end{eqnarray}$$ We have  $\operatorname{Ext}^{2}({\mathcal{V}},{\mathcal{V}}(-L))=0$ by the assumption that
$\operatorname{Ext}^{2}({\mathcal{V}},{\mathcal{V}}(-L))=0$ by the assumption that  ${\mathcal{V}}$ is
${\mathcal{V}}$ is  $L$-prioritary and
$L$-prioritary and  $\operatorname{Ext}^{1}({\mathcal{V}},{\mathcal{O}}_{p})=0$ because
$\operatorname{Ext}^{1}({\mathcal{V}},{\mathcal{O}}_{p})=0$ because  ${\mathcal{V}}$ is locally free at the general point
${\mathcal{V}}$ is locally free at the general point  $p$. We conclude that
$p$. We conclude that  ${\mathcal{V}}^{\prime }$ is
${\mathcal{V}}^{\prime }$ is  $L$-prioritary.
$L$-prioritary.
(2) The first equality follows from the exact sequence, and Riemann–Roch gives the second.
(3) This follows immediately from the long exact sequence in cohomology.
(4) Consider the long exact sequence in cohomology
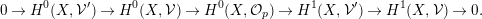 $$\begin{eqnarray}0\rightarrow H^{0}(X,{\mathcal{V}}^{\prime })\rightarrow H^{0}(X,{\mathcal{V}})\rightarrow H^{0}(X,{\mathcal{O}}_{p})\rightarrow H^{1}(X,{\mathcal{V}}^{\prime })\rightarrow H^{1}(X,{\mathcal{V}})\rightarrow 0.\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow H^{0}(X,{\mathcal{V}}^{\prime })\rightarrow H^{0}(X,{\mathcal{V}})\rightarrow H^{0}(X,{\mathcal{O}}_{p})\rightarrow H^{1}(X,{\mathcal{V}}^{\prime })\rightarrow H^{1}(X,{\mathcal{V}})\rightarrow 0.\end{eqnarray}$$ If  $H^{0}(X,{\mathcal{V}})=0$, then
$H^{0}(X,{\mathcal{V}})=0$, then  $H^{0}(X,{\mathcal{V}}^{\prime })=0$. Suppose
$H^{0}(X,{\mathcal{V}}^{\prime })=0$. Suppose  $H^{0}(X,{\mathcal{V}})\neq 0$ and
$H^{0}(X,{\mathcal{V}})\neq 0$ and  $H^{1}(X,{\mathcal{V}})=0$. Then by the choice of
$H^{1}(X,{\mathcal{V}})=0$. Then by the choice of  $\unicode[STIX]{x1D719}:{\mathcal{V}}\rightarrow {\mathcal{O}}_{p}$, the map
$\unicode[STIX]{x1D719}:{\mathcal{V}}\rightarrow {\mathcal{O}}_{p}$, the map  $H^{0}(X,{\mathcal{V}})\rightarrow H^{0}(X,{\mathcal{O}}_{p})=\mathbb{C}$ is surjective. It follows that
$H^{0}(X,{\mathcal{V}})\rightarrow H^{0}(X,{\mathcal{O}}_{p})=\mathbb{C}$ is surjective. It follows that  $H^{1}(X,{\mathcal{V}}^{\prime })=0$.◻
$H^{1}(X,{\mathcal{V}}^{\prime })=0$.◻
2.4 Exceptional collections
We refer the reader to [Reference Coskun and HuizengaCH16] for more details on the following discussion. We use exceptional collections of sheaves on  $\mathbb{F}_{e}$ as basic building blocks for constructing sheaves with useful properties.
$\mathbb{F}_{e}$ as basic building blocks for constructing sheaves with useful properties.
Definition 2.8. A coherent sheaf  ${\mathcal{E}}$ is called exceptional if
${\mathcal{E}}$ is called exceptional if  $\operatorname{Ext}^{i}({\mathcal{E}},{\mathcal{E}})=0$ for
$\operatorname{Ext}^{i}({\mathcal{E}},{\mathcal{E}})=0$ for  $i\geqslant 1$ and
$i\geqslant 1$ and  $\operatorname{Hom}({\mathcal{E}},{\mathcal{E}})=\mathbb{C}$. An ordered collection of exceptional objects
$\operatorname{Hom}({\mathcal{E}},{\mathcal{E}})=\mathbb{C}$. An ordered collection of exceptional objects  ${\mathcal{E}}_{1},\ldots ,{\mathcal{E}}_{m}$ is an exceptional collection if
${\mathcal{E}}_{1},\ldots ,{\mathcal{E}}_{m}$ is an exceptional collection if  $\operatorname{Ext}^{i}({\mathcal{E}}_{t},{\mathcal{E}}_{s})=0$ for
$\operatorname{Ext}^{i}({\mathcal{E}}_{t},{\mathcal{E}}_{s})=0$ for  $s<t$ and all
$s<t$ and all  $i$. The exceptional collection is strong if in addition
$i$. The exceptional collection is strong if in addition  $\operatorname{Ext}^{i}({\mathcal{E}}_{s},{\mathcal{E}}_{t})=0$ for
$\operatorname{Ext}^{i}({\mathcal{E}}_{s},{\mathcal{E}}_{t})=0$ for  $s<t$ and
$s<t$ and  $i\not =0$.
$i\not =0$.
Example 2.9. On  $\mathbb{F}_{e}$, the line bundles
$\mathbb{F}_{e}$, the line bundles
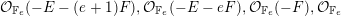 $$\begin{eqnarray}{\mathcal{O}}_{\mathbb{F}_{e}}(-E-(e+1)F),{\mathcal{O}}_{\mathbb{F}_{e}}(-E-eF),{\mathcal{O}}_{\mathbb{F}_{e}}(-F),{\mathcal{O}}_{\mathbb{F}_{e}}\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{O}}_{\mathbb{F}_{e}}(-E-(e+1)F),{\mathcal{O}}_{\mathbb{F}_{e}}(-E-eF),{\mathcal{O}}_{\mathbb{F}_{e}}(-F),{\mathcal{O}}_{\mathbb{F}_{e}}\end{eqnarray}$$give a strong exceptional collection (see [Reference Coskun and HuizengaCH16, Example 3.2]).
In [Reference Coskun and HuizengaCH16], the majority of the following result was proved.
Theorem 2.10. Let  ${\mathcal{E}}_{1},\ldots ,{\mathcal{E}}_{m},{\mathcal{F}}_{1},\ldots ,{\mathcal{F}}_{n}$ be a strong exceptional collection of vector bundles on a surface
${\mathcal{E}}_{1},\ldots ,{\mathcal{E}}_{m},{\mathcal{F}}_{1},\ldots ,{\mathcal{F}}_{n}$ be a strong exceptional collection of vector bundles on a surface  $X$, partitioned into two blocks, and let
$X$, partitioned into two blocks, and let  $L$ be a line bundle on
$L$ be a line bundle on  $X$. Assume that
$X$. Assume that
(1) The sheaf
 ${\mathcal{H}}\mathit{om}({\mathcal{E}}_{i},{\mathcal{F}}_{j})$ is globally generated for all
${\mathcal{H}}\mathit{om}({\mathcal{E}}_{i},{\mathcal{F}}_{j})$ is globally generated for all  $i,j$,
$i,j$,(2)
 $\operatorname{Ext}^{1}({\mathcal{E}}_{i},{\mathcal{F}}_{j}(-L))=0$ for all
$\operatorname{Ext}^{1}({\mathcal{E}}_{i},{\mathcal{F}}_{j}(-L))=0$ for all  $i,j$, and
$i,j$, and(3)
 $\operatorname{Ext}^{2}({\mathcal{F}}_{i},{\mathcal{F}}_{j}(-L))=0$ for all
$\operatorname{Ext}^{2}({\mathcal{F}}_{i},{\mathcal{F}}_{j}(-L))=0$ for all  $i,j$.
$i,j$.
Suppose  $a_{1},\ldots ,a_{m}$ and
$a_{1},\ldots ,a_{m}$ and  $b_{1},\ldots ,b_{n}$ are nonnegative integers such that
$b_{1},\ldots ,b_{n}$ are nonnegative integers such that  $\sum b_{j}r({\mathcal{F}}_{j})-\sum a_{i}r({\mathcal{E}}_{i})>0$, and let
$\sum b_{j}r({\mathcal{F}}_{j})-\sum a_{i}r({\mathcal{E}}_{i})>0$, and let
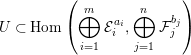 $$\begin{eqnarray}U\subset \operatorname{Hom}\left(\bigoplus _{i=1}^{m}{\mathcal{E}}_{i}^{a_{i}},\bigoplus _{j=1}^{n}{\mathcal{F}}_{j}^{b_{j}}\right)\end{eqnarray}$$
$$\begin{eqnarray}U\subset \operatorname{Hom}\left(\bigoplus _{i=1}^{m}{\mathcal{E}}_{i}^{a_{i}},\bigoplus _{j=1}^{n}{\mathcal{F}}_{j}^{b_{j}}\right)\end{eqnarray}$$ be the open subset parameterizing injective sheaf maps with torsion-free cokernel. For  $\unicode[STIX]{x1D719}\in U$, let
$\unicode[STIX]{x1D719}\in U$, let  ${\mathcal{V}}_{\unicode[STIX]{x1D719}}$ be the cokernel:
${\mathcal{V}}_{\unicode[STIX]{x1D719}}$ be the cokernel:
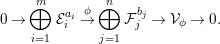 $$\begin{eqnarray}0\rightarrow \bigoplus _{i=1}^{m}{\mathcal{E}}_{i}^{a_{i}}\stackrel{\unicode[STIX]{x1D719}}{\rightarrow }\bigoplus _{j=1}^{n}{\mathcal{F}}_{j}^{b_{j}}\rightarrow {\mathcal{V}}_{\unicode[STIX]{x1D719}}\rightarrow 0.\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow \bigoplus _{i=1}^{m}{\mathcal{E}}_{i}^{a_{i}}\stackrel{\unicode[STIX]{x1D719}}{\rightarrow }\bigoplus _{j=1}^{n}{\mathcal{F}}_{j}^{b_{j}}\rightarrow {\mathcal{V}}_{\unicode[STIX]{x1D719}}\rightarrow 0.\end{eqnarray}$$ Then  $U$ is nonempty, and the family
$U$ is nonempty, and the family  ${\mathcal{V}}_{\unicode[STIX]{x1D719}}/U$ is a complete family of
${\mathcal{V}}_{\unicode[STIX]{x1D719}}/U$ is a complete family of  $L$-prioritary sheaves.
$L$-prioritary sheaves.
Proof. If  $r({\mathcal{V}}_{\unicode[STIX]{x1D719}})=\sum b_{j}r({\mathcal{F}}_{j})-\sum a_{i}r({\mathcal{E}}_{i})\geqslant 2$, then this is [Reference Coskun and HuizengaCH16, Proposition 3.6]. When
$r({\mathcal{V}}_{\unicode[STIX]{x1D719}})=\sum b_{j}r({\mathcal{F}}_{j})-\sum a_{i}r({\mathcal{E}}_{i})\geqslant 2$, then this is [Reference Coskun and HuizengaCH16, Proposition 3.6]. When  $r({\mathcal{V}}_{\unicode[STIX]{x1D719}})=1$, everything follows as in the
$r({\mathcal{V}}_{\unicode[STIX]{x1D719}})=1$, everything follows as in the  $r({\mathcal{V}}_{\unicode[STIX]{x1D719}})\geqslant 2$ case, except we must verify that
$r({\mathcal{V}}_{\unicode[STIX]{x1D719}})\geqslant 2$ case, except we must verify that  ${\mathcal{V}}_{\unicode[STIX]{x1D719}}$ is still torsion-free. The rank of
${\mathcal{V}}_{\unicode[STIX]{x1D719}}$ is still torsion-free. The rank of  $\unicode[STIX]{x1D719}$ only drops in codimension
$\unicode[STIX]{x1D719}$ only drops in codimension  $2$, so any torsion subsheaf
$2$, so any torsion subsheaf  ${\mathcal{T}}\subset {\mathcal{V}}_{\unicode[STIX]{x1D719}}$ has
${\mathcal{T}}\subset {\mathcal{V}}_{\unicode[STIX]{x1D719}}$ has  $0$-dimensional support. If
$0$-dimensional support. If  ${\mathcal{T}}\neq 0$ and
${\mathcal{T}}\neq 0$ and  $M$ is any line bundle, then
$M$ is any line bundle, then  $H^{0}(X,{\mathcal{T}}\otimes M)\neq 0$ and hence
$H^{0}(X,{\mathcal{T}}\otimes M)\neq 0$ and hence  $H^{0}(X,{\mathcal{V}}_{\unicode[STIX]{x1D719}}\otimes M)\neq 0$. However, if
$H^{0}(X,{\mathcal{V}}_{\unicode[STIX]{x1D719}}\otimes M)\neq 0$. However, if  $M$ is sufficiently anti-ample, then tensoring the resolution of
$M$ is sufficiently anti-ample, then tensoring the resolution of  ${\mathcal{V}}_{\unicode[STIX]{x1D719}}$ by
${\mathcal{V}}_{\unicode[STIX]{x1D719}}$ by  $M$ shows
$M$ shows  $H^{0}(X,{\mathcal{V}}_{\unicode[STIX]{x1D719}}\otimes M)=0$. Therefore,
$H^{0}(X,{\mathcal{V}}_{\unicode[STIX]{x1D719}}\otimes M)=0$. Therefore,  ${\mathcal{T}}=0$.◻
${\mathcal{T}}=0$.◻
2.5 Globally generated vector bundles
We now recall some properties of globally generated sheaves for use in §5. A coherent sheaf  ${\mathcal{V}}$ on a projective variety
${\mathcal{V}}$ on a projective variety  $X$ over a field
$X$ over a field  $k$ is globally generated if the evaluation map
$k$ is globally generated if the evaluation map
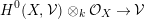 $$\begin{eqnarray}H^{0}(X,{\mathcal{V}})\otimes _{k}{\mathcal{O}}_{X}\rightarrow {\mathcal{V}}\end{eqnarray}$$
$$\begin{eqnarray}H^{0}(X,{\mathcal{V}})\otimes _{k}{\mathcal{O}}_{X}\rightarrow {\mathcal{V}}\end{eqnarray}$$is surjective. The following lemma is immediate.
Lemma 2.11. Any quotient of a globally generated sheaf is globally generated.
If  ${\mathcal{V}}$ is globally generated, then there is an obvious restriction on
${\mathcal{V}}$ is globally generated, then there is an obvious restriction on  $c_{1}({\mathcal{V}})$.
$c_{1}({\mathcal{V}})$.
Lemma 2.12. Let  ${\mathcal{V}}$ be a globally generated vector bundle on
${\mathcal{V}}$ be a globally generated vector bundle on  $X$. Then for every curve
$X$. Then for every curve  $C\subset X$, we have
$C\subset X$, we have
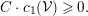 $$\begin{eqnarray}C\cdot c_{1}({\mathcal{V}})\geqslant 0.\end{eqnarray}$$
$$\begin{eqnarray}C\cdot c_{1}({\mathcal{V}})\geqslant 0.\end{eqnarray}$$Proof. The standard short exact sequence
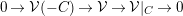 $$\begin{eqnarray}0\rightarrow {\mathcal{V}}(-C)\rightarrow {\mathcal{V}}\rightarrow {\mathcal{V}}|_{C}\rightarrow 0\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow {\mathcal{V}}(-C)\rightarrow {\mathcal{V}}\rightarrow {\mathcal{V}}|_{C}\rightarrow 0\end{eqnarray}$$ implies that  ${\mathcal{V}}|_{C}$ is a quotient of
${\mathcal{V}}|_{C}$ is a quotient of  ${\mathcal{V}}$. Hence, by Lemma 2.11,
${\mathcal{V}}$. Hence, by Lemma 2.11,  ${\mathcal{V}}|_{C}$ is globally generated. Since a globally generated vector bundle on a curve has nonnegative degree, we conclude that
${\mathcal{V}}|_{C}$ is globally generated. Since a globally generated vector bundle on a curve has nonnegative degree, we conclude that  $C\cdot c_{1}({\mathcal{V}})\geqslant 0.$ ◻
$C\cdot c_{1}({\mathcal{V}})\geqslant 0.$ ◻
We warn that while many properties of sheaves that we consider in this paper are open properties, the property of being globally generated is not in general open. However, in a family  ${\mathcal{V}}/S$ of sheaves with no higher cohomology, the locus of globally generated sheaves is clearly open. The next example shows that in an arbitrary family the locus of globally generated sheaves can fail to be open.
${\mathcal{V}}/S$ of sheaves with no higher cohomology, the locus of globally generated sheaves is clearly open. The next example shows that in an arbitrary family the locus of globally generated sheaves can fail to be open.
Example 2.13. On  $\mathbb{P}^{2}$, the locus in
$\mathbb{P}^{2}$, the locus in  $M(\mathbf{v})$ of globally generated semistable sheaves is not generally open, and even if it is nonempty, it need not be dense. For example, for any
$M(\mathbf{v})$ of globally generated semistable sheaves is not generally open, and even if it is nonempty, it need not be dense. For example, for any  $d\geqslant 1$ the bundle
$d\geqslant 1$ the bundle  ${\mathcal{V}}$
${\mathcal{V}}$
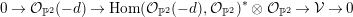 $$\begin{eqnarray}0\rightarrow {\mathcal{O}}_{\mathbb{P}^{2}}(-d)\rightarrow \operatorname{Hom}({\mathcal{O}}_{\mathbb{P}^{2}}(-d),{\mathcal{O}}_{\mathbb{P}^{2}})^{\ast }\otimes {\mathcal{O}}_{\mathbb{ P}^{2}}\rightarrow {\mathcal{V}}\rightarrow 0\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow {\mathcal{O}}_{\mathbb{P}^{2}}(-d)\rightarrow \operatorname{Hom}({\mathcal{O}}_{\mathbb{P}^{2}}(-d),{\mathcal{O}}_{\mathbb{P}^{2}})^{\ast }\otimes {\mathcal{O}}_{\mathbb{ P}^{2}}\rightarrow {\mathcal{V}}\rightarrow 0\end{eqnarray}$$ given by the cokernel of the coevaluation map is globally generated and semistable [Reference Le PotierLeP97, Lemma 9.2.3]. Let  $\mathbf{v}=\operatorname{ch}{\mathcal{V}}$. By the Brill–Noether theorem of Göttsche and Hirschowitz [Reference Göttsche and HirschowitzGHi94], a general sheaf in
$\mathbf{v}=\operatorname{ch}{\mathcal{V}}$. By the Brill–Noether theorem of Göttsche and Hirschowitz [Reference Göttsche and HirschowitzGHi94], a general sheaf in  $M(\mathbf{v})$ has only one nonzero cohomology group.
$M(\mathbf{v})$ has only one nonzero cohomology group.
∙ If
 $d=1$ or
$d=1$ or  $2$, then the bundle
$2$, then the bundle  ${\mathcal{V}}$ is exceptional, and
${\mathcal{V}}$ is exceptional, and  $M(\mathbf{v})=\{[{\mathcal{V}}]\}$ is a point.
$M(\mathbf{v})=\{[{\mathcal{V}}]\}$ is a point.∙ If
 $d=3$, then
$d=3$, then  $\unicode[STIX]{x1D712}(\mathbf{v})=r(\mathbf{v})$, the moduli space
$\unicode[STIX]{x1D712}(\mathbf{v})=r(\mathbf{v})$, the moduli space  $M(\mathbf{v})$ is positive-dimensional, and the general sheaf in
$M(\mathbf{v})$ is positive-dimensional, and the general sheaf in  $M(\mathbf{v})$ has
$M(\mathbf{v})$ has  $r(\mathbf{v})$ sections but is not globally generated.
$r(\mathbf{v})$ sections but is not globally generated.∙ If
 $d\geqslant 4$, then
$d\geqslant 4$, then  $\unicode[STIX]{x1D712}(\mathbf{v})=3d<\binom{d+2}{2}-1=r(\mathbf{v})$ and the general sheaf does not even have
$\unicode[STIX]{x1D712}(\mathbf{v})=3d<\binom{d+2}{2}-1=r(\mathbf{v})$ and the general sheaf does not even have  $r(\mathbf{v})$ sections, so has no hope of being globally generated.
$r(\mathbf{v})$ sections, so has no hope of being globally generated.
Thus, sheaves with “extra” sections can be globally generated even if the general sheaf is not.
3 The Brill–Noether theorem
In this section, we prove the Brill–Noether theorem for vector bundles on Hirzebruch surfaces and compute the Betti numbers of a general sheaf. The next result summarizes the various results in this section; it is instructive to compare the statement with the line bundle case, Theorem 2.1.
Theorem 3.1. Let  $\mathbf{v}\in K(\mathbb{F}_{e})$ be a Chern character with positive rank
$\mathbf{v}\in K(\mathbb{F}_{e})$ be a Chern character with positive rank  $r=r(\mathbf{v})$ and
$r=r(\mathbf{v})$ and  $\unicode[STIX]{x1D6E5}(\mathbf{v})\geqslant 0$. Then the stack
$\unicode[STIX]{x1D6E5}(\mathbf{v})\geqslant 0$. Then the stack  ${\mathcal{P}}_{F}(\mathbf{v})$ is nonempty and irreducible. Let
${\mathcal{P}}_{F}(\mathbf{v})$ is nonempty and irreducible. Let  ${\mathcal{V}}\in {\mathcal{P}}_{F}(\mathbf{v})$ be a general sheaf.
${\mathcal{V}}\in {\mathcal{P}}_{F}(\mathbf{v})$ be a general sheaf.
(1) If we write
 $\unicode[STIX]{x1D708}(\mathbf{v})=(k/r)E+(l/r)F$, then
$\unicode[STIX]{x1D708}(\mathbf{v})=(k/r)E+(l/r)F$, then  $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D712}(\mathbf{v}) & = & \displaystyle r(P(\unicode[STIX]{x1D708}(\mathbf{v}))-\unicode[STIX]{x1D6E5}(\mathbf{v}))\nonumber\\ \displaystyle & = & \displaystyle r\left(\left(\frac{k}{r}+1\right)\left(\frac{l}{r}+1\right)-\frac{ek}{2r}\left(\frac{k}{r}+1\right)-\unicode[STIX]{x1D6E5}(\mathbf{v})\right)\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D712}(\mathbf{v}) & = & \displaystyle r(P(\unicode[STIX]{x1D708}(\mathbf{v}))-\unicode[STIX]{x1D6E5}(\mathbf{v}))\nonumber\\ \displaystyle & = & \displaystyle r\left(\left(\frac{k}{r}+1\right)\left(\frac{l}{r}+1\right)-\frac{ek}{2r}\left(\frac{k}{r}+1\right)-\unicode[STIX]{x1D6E5}(\mathbf{v})\right)\nonumber\end{eqnarray}$$(2) If
 $\unicode[STIX]{x1D708}(\mathbf{v})\cdot F\geqslant -1$, then
$\unicode[STIX]{x1D708}(\mathbf{v})\cdot F\geqslant -1$, then  $h^{2}(\mathbb{F}_{e},{\mathcal{V}})=0$.
$h^{2}(\mathbb{F}_{e},{\mathcal{V}})=0$.(3) If
 $\unicode[STIX]{x1D708}(\mathbf{v})\cdot F\leqslant -1$, then
$\unicode[STIX]{x1D708}(\mathbf{v})\cdot F\leqslant -1$, then  $h^{0}(\mathbb{F}_{e},{\mathcal{V}})=0$.
$h^{0}(\mathbb{F}_{e},{\mathcal{V}})=0$.(4) In particular, if
 $\unicode[STIX]{x1D708}(\mathbf{v})\cdot F=-1$, then
$\unicode[STIX]{x1D708}(\mathbf{v})\cdot F=-1$, then  $h^{1}(\mathbb{F}_{e},{\mathcal{V}})=-\unicode[STIX]{x1D712}(\mathbf{v})$ and all other cohomology vanishes.
$h^{1}(\mathbb{F}_{e},{\mathcal{V}})=-\unicode[STIX]{x1D712}(\mathbf{v})$ and all other cohomology vanishes.Now suppose
 $\unicode[STIX]{x1D708}(\mathbf{v})\cdot F>-1$. Then
$\unicode[STIX]{x1D708}(\mathbf{v})\cdot F>-1$. Then  $H^{2}(\mathbb{F}_{e},{\mathcal{V}})=0$, so either of the numbers
$H^{2}(\mathbb{F}_{e},{\mathcal{V}})=0$, so either of the numbers  $h^{0}(\mathbb{F}_{e},{\mathcal{V}})$ or
$h^{0}(\mathbb{F}_{e},{\mathcal{V}})$ or  $h^{1}(\mathbb{F}_{e},{\mathcal{V}})$ determine the Betti numbers of
$h^{1}(\mathbb{F}_{e},{\mathcal{V}})$ determine the Betti numbers of  ${\mathcal{V}}$. These can be determined as follows.
${\mathcal{V}}$. These can be determined as follows.(5) If
 $\unicode[STIX]{x1D708}(\mathbf{v})\cdot E\geqslant -1$, then
$\unicode[STIX]{x1D708}(\mathbf{v})\cdot E\geqslant -1$, then  ${\mathcal{V}}$ has at most one nonzero cohomology group. Thus if
${\mathcal{V}}$ has at most one nonzero cohomology group. Thus if  $\unicode[STIX]{x1D712}(\mathbf{v})\geqslant 0$, then
$\unicode[STIX]{x1D712}(\mathbf{v})\geqslant 0$, then  $h^{0}(\mathbb{F}_{e},{\mathcal{V}})=\unicode[STIX]{x1D712}(\mathbf{v})$, and if
$h^{0}(\mathbb{F}_{e},{\mathcal{V}})=\unicode[STIX]{x1D712}(\mathbf{v})$, and if  $\unicode[STIX]{x1D712}(\mathbf{v})\leqslant 0$, then
$\unicode[STIX]{x1D712}(\mathbf{v})\leqslant 0$, then  $h^{1}(\mathbb{F}_{e},{\mathcal{V}})=-\unicode[STIX]{x1D712}(\mathbf{v})$.
$h^{1}(\mathbb{F}_{e},{\mathcal{V}})=-\unicode[STIX]{x1D712}(\mathbf{v})$.(6) If
 $\unicode[STIX]{x1D708}(\mathbf{v})\cdot E<-1$, then
$\unicode[STIX]{x1D708}(\mathbf{v})\cdot E<-1$, then  $H^{0}(\mathbb{F}_{e},{\mathcal{V}})\cong H^{0}(\mathbb{F}_{e},{\mathcal{V}}(-E))$, and so the Betti numbers of
$H^{0}(\mathbb{F}_{e},{\mathcal{V}})\cong H^{0}(\mathbb{F}_{e},{\mathcal{V}}(-E))$, and so the Betti numbers of  ${\mathcal{V}}$ can be determined inductively using (3) and (5).
${\mathcal{V}}$ can be determined inductively using (3) and (5).
(If  $\unicode[STIX]{x1D708}(\mathbf{v})\cdot F<-1$ and
$\unicode[STIX]{x1D708}(\mathbf{v})\cdot F<-1$ and  $r(\mathbf{v})\geqslant 2$, then the cohomology of
$r(\mathbf{v})\geqslant 2$, then the cohomology of  ${\mathcal{V}}$ can be determined by Serre duality.)
${\mathcal{V}}$ can be determined by Serre duality.)
Remark 3.2. In particular, if  $H$ is an arbitrary ample divisor on
$H$ is an arbitrary ample divisor on  $\mathbb{F}_{e}$ and there are
$\mathbb{F}_{e}$ and there are  $\unicode[STIX]{x1D707}_{H}$-semistable sheaves of character
$\unicode[STIX]{x1D707}_{H}$-semistable sheaves of character  $\mathbf{v}$, then Theorem 3.1 allows us to compute the Betti numbers of a general sheaf
$\mathbf{v}$, then Theorem 3.1 allows us to compute the Betti numbers of a general sheaf  ${\mathcal{V}}\in M_{H}^{\unicode[STIX]{x1D707}\text{-}\mathit{ss}}(\mathbf{v})$.
${\mathcal{V}}\in M_{H}^{\unicode[STIX]{x1D707}\text{-}\mathit{ss}}(\mathbf{v})$.
Statement (1) of the theorem is just Riemann–Roch, reproduced here for the reader’s convenience. The locus of sheaves  ${\mathcal{V}}\in {\mathcal{P}}_{F}(\mathbf{v})$ satisfying each of the statements (2)–(5) of the theorem is open in the stack
${\mathcal{V}}\in {\mathcal{P}}_{F}(\mathbf{v})$ satisfying each of the statements (2)–(5) of the theorem is open in the stack  ${\mathcal{P}}_{F}(\mathbf{v})$, so it suffices to produce a single sheaf
${\mathcal{P}}_{F}(\mathbf{v})$, so it suffices to produce a single sheaf  ${\mathcal{V}}\in {\mathcal{P}}_{F}(\mathbf{v})$ with the given cohomology. We construct such sheaves by using direct sums of line bundles as basic building blocks (§3.1) and applying elementary modifications to them (§3.2). Statement (6) follows easily from the observation that for a general
${\mathcal{V}}\in {\mathcal{P}}_{F}(\mathbf{v})$ with the given cohomology. We construct such sheaves by using direct sums of line bundles as basic building blocks (§3.1) and applying elementary modifications to them (§3.2). Statement (6) follows easily from the observation that for a general  ${\mathcal{V}}\in {\mathcal{P}}_{F}(\mathbf{v})$ the restriction
${\mathcal{V}}\in {\mathcal{P}}_{F}(\mathbf{v})$ the restriction  ${\mathcal{V}}|_{E}$ is balanced (see Corollary 3.6).
${\mathcal{V}}|_{E}$ is balanced (see Corollary 3.6).
3.1 Prioritary direct sums of line bundles
We first show that for any rank  $r\geqslant 1$ and slope
$r\geqslant 1$ and slope  $\unicode[STIX]{x1D708}=(k/r)E+(l/r)F$, there is a prioritary direct sum of line bundles with
$\unicode[STIX]{x1D708}=(k/r)E+(l/r)F$, there is a prioritary direct sum of line bundles with  $\unicode[STIX]{x1D6E5}\leqslant 0$. We identify
$\unicode[STIX]{x1D6E5}\leqslant 0$. We identify  $N^{1}(\mathbb{F}_{e})_{\mathbb{Q}}\cong \mathbb{Q}^{2}$ with the
$N^{1}(\mathbb{F}_{e})_{\mathbb{Q}}\cong \mathbb{Q}^{2}$ with the  $(k/r,l/r)$-plane. The particular line bundles we use depend on
$(k/r,l/r)$-plane. The particular line bundles we use depend on  $(k/r,l/r)$. The next lemma shows that if this point is in a certain triangular region, then we can find such a direct sum of line bundles.
$(k/r,l/r)$. The next lemma shows that if this point is in a certain triangular region, then we can find such a direct sum of line bundles.
Lemma 3.3. Let  $a,b,c\geqslant 0$ be nonnegative integers, and let
$a,b,c\geqslant 0$ be nonnegative integers, and let
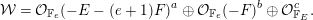 $$\begin{eqnarray}{\mathcal{W}}={\mathcal{O}}_{\mathbb{F}_{e}}(-E-(e+1)F)^{a}\oplus {\mathcal{O}}_{\mathbb{F}_{e}}(-F)^{b}\oplus {\mathcal{O}}_{\mathbb{F}_{E}}^{c}.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{W}}={\mathcal{O}}_{\mathbb{F}_{e}}(-E-(e+1)F)^{a}\oplus {\mathcal{O}}_{\mathbb{F}_{e}}(-F)^{b}\oplus {\mathcal{O}}_{\mathbb{F}_{E}}^{c}.\end{eqnarray}$$(1) The bundle
 ${\mathcal{W}}$ is
${\mathcal{W}}$ is  $F$-prioritary and
$F$-prioritary and  $E$-prioritary, and
$E$-prioritary, and  ${\mathcal{W}}$ has no higher cohomology.
${\mathcal{W}}$ has no higher cohomology.(2) We have
 $\unicode[STIX]{x1D6E5}({\mathcal{W}})\leqslant 0$.
$\unicode[STIX]{x1D6E5}({\mathcal{W}})\leqslant 0$.(3) Let
 $r\geqslant 1$ and represent a total slope
$r\geqslant 1$ and represent a total slope  $(k/r)E+(l/r)F\in N^{1}(\mathbb{F}_{e})_{\mathbb{Q}}$ by the point
$(k/r)E+(l/r)F\in N^{1}(\mathbb{F}_{e})_{\mathbb{Q}}$ by the point  $(k/r,l/r)\in \mathbb{Q}^{2}$. If
$(k/r,l/r)\in \mathbb{Q}^{2}$. If  $(k/r,l/r)$ is in the convex region with vertices then it is the slope of a rank
$(k/r,l/r)$ is in the convex region with vertices then it is the slope of a rank $$\begin{eqnarray}(-1,-e-1),\,(0,-1),\,(0,0),\end{eqnarray}$$
$$\begin{eqnarray}(-1,-e-1),\,(0,-1),\,(0,0),\end{eqnarray}$$ $r$ bundle
$r$ bundle  ${\mathcal{W}}$ as above.
${\mathcal{W}}$ as above.
Proof. (1) The vector space  $\operatorname{Ext}^{2}({\mathcal{W}},{\mathcal{W}}(-F))$ is a direct sum of vector spaces of the form
$\operatorname{Ext}^{2}({\mathcal{W}},{\mathcal{W}}(-F))$ is a direct sum of vector spaces of the form  $H^{2}(\mathbb{F}_{e},{\mathcal{O}}_{\mathbb{F}_{e}}(\unicode[STIX]{x1D6FC}E+\unicode[STIX]{x1D6FD}F))$ where
$H^{2}(\mathbb{F}_{e},{\mathcal{O}}_{\mathbb{F}_{e}}(\unicode[STIX]{x1D6FC}E+\unicode[STIX]{x1D6FD}F))$ where  $\unicode[STIX]{x1D6FC}\geqslant -1$, and these are zero. Therefore,
$\unicode[STIX]{x1D6FC}\geqslant -1$, and these are zero. Therefore,  ${\mathcal{W}}$ is
${\mathcal{W}}$ is  $F$-prioritary. Similarly, the vector space
$F$-prioritary. Similarly, the vector space  $\operatorname{Ext}^{2}({\mathcal{W}},{\mathcal{W}}(-E))$ is a direct sum of vector spaces of the form
$\operatorname{Ext}^{2}({\mathcal{W}},{\mathcal{W}}(-E))$ is a direct sum of vector spaces of the form  $H^{2}(\mathbb{F}_{e},{\mathcal{O}}_{\mathbb{F}_{e}}(\unicode[STIX]{x1D6FC}E+\unicode[STIX]{x1D6FD}F))$ where
$H^{2}(\mathbb{F}_{e},{\mathcal{O}}_{\mathbb{F}_{e}}(\unicode[STIX]{x1D6FC}E+\unicode[STIX]{x1D6FD}F))$ where  $\unicode[STIX]{x1D6FD}\geqslant -e-1$, and these are again zero. Therefore,
$\unicode[STIX]{x1D6FD}\geqslant -e-1$, and these are again zero. Therefore,  ${\mathcal{W}}$ is
${\mathcal{W}}$ is  $E$-prioritary. The statement on cohomology follows at once from Theorem 2.1.
$E$-prioritary. The statement on cohomology follows at once from Theorem 2.1.
(2) We compute
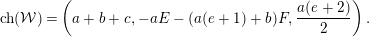 $$\begin{eqnarray}\operatorname{ch}({\mathcal{W}})=\left(a+b+c,-aE-(a(e+1)+b)F,\frac{a(e+2)}{2}\right).\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{ch}({\mathcal{W}})=\left(a+b+c,-aE-(a(e+1)+b)F,\frac{a(e+2)}{2}\right).\end{eqnarray}$$Then
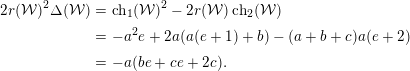 $$\begin{eqnarray}\displaystyle 2r({\mathcal{W}})^{2}\unicode[STIX]{x1D6E5}({\mathcal{W}}) & = & \displaystyle \operatorname{ch}_{1}({\mathcal{W}})^{2}-2r({\mathcal{W}})\operatorname{ch}_{2}({\mathcal{W}})\nonumber\\ \displaystyle & = & \displaystyle -a^{2}e+2a(a(e+1)+b)-(a+b+c)a(e+2)\nonumber\\ \displaystyle & = & \displaystyle -a(be+ce+2c).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 2r({\mathcal{W}})^{2}\unicode[STIX]{x1D6E5}({\mathcal{W}}) & = & \displaystyle \operatorname{ch}_{1}({\mathcal{W}})^{2}-2r({\mathcal{W}})\operatorname{ch}_{2}({\mathcal{W}})\nonumber\\ \displaystyle & = & \displaystyle -a^{2}e+2a(a(e+1)+b)-(a+b+c)a(e+2)\nonumber\\ \displaystyle & = & \displaystyle -a(be+ce+2c).\nonumber\end{eqnarray}$$ Therefore,  $\unicode[STIX]{x1D6E5}({\mathcal{W}})\leqslant 0$.
$\unicode[STIX]{x1D6E5}({\mathcal{W}})\leqslant 0$.
(3) The slope  $(k/r,l/r)$ is in the convex region spanned by
$(k/r,l/r)$ is in the convex region spanned by  $(-1,-e-1)$,
$(-1,-e-1)$,  $(0,-1)$ and
$(0,-1)$ and  $(0,0)$ if and only if the vector
$(0,0)$ if and only if the vector  $(k,l,r)$ is in the cone spanned by
$(k,l,r)$ is in the cone spanned by  $(-1,-e-1,1)$,
$(-1,-e-1,1)$,  $(0,-1,1)$, and
$(0,-1,1)$, and  $(0,0,1)$. This happens if and only if the linear system
$(0,0,1)$. This happens if and only if the linear system
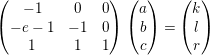 $$\begin{eqnarray}\left(\begin{array}{@{}ccc@{}}-1 & 0 & 0\\ -e-1 & -1 & 0\\ 1 & 1 & 1\end{array}\right)\left(\begin{array}{@{}c@{}}a\\ b\\ c\end{array}\right)=\left(\begin{array}{@{}c@{}}k\\ l\\ r\end{array}\right)\end{eqnarray}$$
$$\begin{eqnarray}\left(\begin{array}{@{}ccc@{}}-1 & 0 & 0\\ -e-1 & -1 & 0\\ 1 & 1 & 1\end{array}\right)\left(\begin{array}{@{}c@{}}a\\ b\\ c\end{array}\right)=\left(\begin{array}{@{}c@{}}k\\ l\\ r\end{array}\right)\end{eqnarray}$$ has a solution  $(a,b,c)\in \mathbb{Q}_{{\geqslant}0}^{3}$. But the matrix is in
$(a,b,c)\in \mathbb{Q}_{{\geqslant}0}^{3}$. But the matrix is in  $\operatorname{SL}_{3}(\mathbb{Z})$, so actually
$\operatorname{SL}_{3}(\mathbb{Z})$, so actually  $(a,b,c)\in \mathbb{Z}_{{\geqslant}0}^{3}$. The corresponding bundle
$(a,b,c)\in \mathbb{Z}_{{\geqslant}0}^{3}$. The corresponding bundle  ${\mathcal{W}}$ has rank
${\mathcal{W}}$ has rank  $r$ and slope
$r$ and slope  $(k/r,l/r)$.◻
$(k/r,l/r)$.◻
By an analogous construction we can further handle slopes lying in a larger quadrilateral region. This quadrilateral has the advantage that its shifts by line bundles tile the whole  $(k/r,l/r)$-plane.
$(k/r,l/r)$-plane.
Corollary 3.4. Suppose  $r\geqslant 1$ and the point
$r\geqslant 1$ and the point  $(k/r,l/r)$ lies in the parallelogram
$(k/r,l/r)$ lies in the parallelogram  $Q$ bounded by the four vertices
$Q$ bounded by the four vertices
 $$\begin{eqnarray}(-1,-e),\quad (0,0),\quad (0,-1)\quad \text{and}\quad (-1,-e-1).\end{eqnarray}$$
$$\begin{eqnarray}(-1,-e),\quad (0,0),\quad (0,-1)\quad \text{and}\quad (-1,-e-1).\end{eqnarray}$$ Then there is a rank  $r$ direct sum
$r$ direct sum  ${\mathcal{W}}$ of copies of the line bundles
${\mathcal{W}}$ of copies of the line bundles
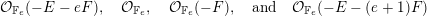 $$\begin{eqnarray}{\mathcal{O}}_{\mathbb{F}_{e}}(-E-eF),\quad {\mathcal{O}}_{\mathbb{F}_{e}},\quad {\mathcal{O}}_{\mathbb{F}_{e}}(-F),\quad \text{and}\quad {\mathcal{O}}_{\mathbb{F}_{e}}(-E-(e+1)F)\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{O}}_{\mathbb{F}_{e}}(-E-eF),\quad {\mathcal{O}}_{\mathbb{F}_{e}},\quad {\mathcal{O}}_{\mathbb{F}_{e}}(-F),\quad \text{and}\quad {\mathcal{O}}_{\mathbb{F}_{e}}(-E-(e+1)F)\end{eqnarray}$$such that
(1)
 $\unicode[STIX]{x1D708}({\mathcal{W}})=(k/r)E+(l/r)F$,
$\unicode[STIX]{x1D708}({\mathcal{W}})=(k/r)E+(l/r)F$,(2)
 ${\mathcal{W}}$ is
${\mathcal{W}}$ is  $F$- and
$F$- and  $E$-prioritary, and
$E$-prioritary, and(3)
 $\unicode[STIX]{x1D6E5}({\mathcal{W}})\leqslant 0$.
$\unicode[STIX]{x1D6E5}({\mathcal{W}})\leqslant 0$.
Proof. The quadrilateral region is split into a lower triangle  $T_{1}$ and an upper triangle
$T_{1}$ and an upper triangle  $T_{2}$ by the line segment from
$T_{2}$ by the line segment from  $(-1,-e-1)$ to
$(-1,-e-1)$ to  $(0,0)$. If
$(0,0)$. If  $(k/r,l/r)$ is in
$(k/r,l/r)$ is in  $T_{1}$, then everything follows from Lemma 3.3.
$T_{1}$, then everything follows from Lemma 3.3.
On the other hand, if  $(k/r,l/r)$ lies in
$(k/r,l/r)$ lies in  $T_{2}$, consider direct sums of the form
$T_{2}$, consider direct sums of the form
 $$\begin{eqnarray}{\mathcal{W}}={\mathcal{O}}_{\mathbb{F}_{e}}^{a}\oplus {\mathcal{O}}_{\mathbb{F}_{e}}(-E-eF)^{b}\oplus {\mathcal{O}}_{\mathbb{F}_{e}}(-E-(e+1)F)^{c}.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{W}}={\mathcal{O}}_{\mathbb{F}_{e}}^{a}\oplus {\mathcal{O}}_{\mathbb{F}_{e}}(-E-eF)^{b}\oplus {\mathcal{O}}_{\mathbb{F}_{e}}(-E-(e+1)F)^{c}.\end{eqnarray}$$Notice that
 $$\begin{eqnarray}({\mathcal{W}}(E+(e+1)F))^{\ast }={\mathcal{O}}_{\mathbb{ F}_{e}}(-E-(e+1)F)^{a}\oplus {\mathcal{O}}_{\mathbb{F}_{e}}(-F)^{b}\oplus {\mathcal{O}}_{F_{e}}^{c}\end{eqnarray}$$
$$\begin{eqnarray}({\mathcal{W}}(E+(e+1)F))^{\ast }={\mathcal{O}}_{\mathbb{ F}_{e}}(-E-(e+1)F)^{a}\oplus {\mathcal{O}}_{\mathbb{F}_{e}}(-F)^{b}\oplus {\mathcal{O}}_{F_{e}}^{c}\end{eqnarray}$$ is of the same form as the line bundles considered in Lemma 3.3. Since tensoring by line bundles and taking duals preserves discriminants and prioritariness, it follows that the integers  $a,b,c$ can be chosen so that
$a,b,c$ can be chosen so that  ${\mathcal{W}}$ has the required properties.◻
${\mathcal{W}}$ has the required properties.◻
3.2 Elementary modifications
When combined with elementary modifications, Corollary 3.4 has many consequences, which we now investigate. The proof of the next corollary is fundamental to all the results which follow and makes crucial use of Lemma 2.7.
Corollary 3.5. Let  $\mathbf{v}\in K(\mathbb{F}_{e})$ be a character of positive rank with
$\mathbf{v}\in K(\mathbb{F}_{e})$ be a character of positive rank with  $\unicode[STIX]{x1D6E5}(\mathbf{v})\geqslant 0$. Then
$\unicode[STIX]{x1D6E5}(\mathbf{v})\geqslant 0$. Then  ${\mathcal{P}}_{F}(\mathbf{v})$ is nonempty.
${\mathcal{P}}_{F}(\mathbf{v})$ is nonempty.
Proof. Since integer translates of the region  $Q$ in Corollary 3.4 tile
$Q$ in Corollary 3.4 tile  $N^{1}(\mathbb{F}_{e})_{\mathbb{Q}}$, we may find a line bundle
$N^{1}(\mathbb{F}_{e})_{\mathbb{Q}}$, we may find a line bundle  $L$ such that
$L$ such that  $\unicode[STIX]{x1D708}(\mathbf{v}(-L))$ lies in
$\unicode[STIX]{x1D708}(\mathbf{v}(-L))$ lies in  $Q$. Then Corollary 3.4 produces an
$Q$. Then Corollary 3.4 produces an  $F$-prioritary sheaf
$F$-prioritary sheaf  ${\mathcal{W}}$ of nonpositive discriminant with
${\mathcal{W}}$ of nonpositive discriminant with  $r({\mathcal{W}}(L))=r(\mathbf{v})$ and
$r({\mathcal{W}}(L))=r(\mathbf{v})$ and  $\unicode[STIX]{x1D708}({\mathcal{W}}(L))=\unicode[STIX]{x1D708}(\mathbf{v})$. Then since
$\unicode[STIX]{x1D708}({\mathcal{W}}(L))=\unicode[STIX]{x1D708}(\mathbf{v})$. Then since  $\unicode[STIX]{x1D6E5}(\mathbf{v})\geqslant 0$, the integer
$\unicode[STIX]{x1D6E5}(\mathbf{v})\geqslant 0$, the integer  $m=\unicode[STIX]{x1D712}({\mathcal{W}}(L))-\unicode[STIX]{x1D712}(\mathbf{v})$ is nonnegative, since
$m=\unicode[STIX]{x1D712}({\mathcal{W}}(L))-\unicode[STIX]{x1D712}(\mathbf{v})$ is nonnegative, since
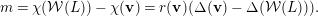 $$\begin{eqnarray}m=\unicode[STIX]{x1D712}({\mathcal{W}}(L))-\unicode[STIX]{x1D712}(\mathbf{v})=r(\mathbf{v})(\unicode[STIX]{x1D6E5}(\mathbf{v})-\unicode[STIX]{x1D6E5}({\mathcal{W}}(L))).\end{eqnarray}$$
$$\begin{eqnarray}m=\unicode[STIX]{x1D712}({\mathcal{W}}(L))-\unicode[STIX]{x1D712}(\mathbf{v})=r(\mathbf{v})(\unicode[STIX]{x1D6E5}(\mathbf{v})-\unicode[STIX]{x1D6E5}({\mathcal{W}}(L))).\end{eqnarray}$$ Thus by Lemma 2.7, if we perform  $m$ general elementary modifications to
$m$ general elementary modifications to  ${\mathcal{W}}(L)$, the resulting sheaf
${\mathcal{W}}(L)$, the resulting sheaf  ${\mathcal{V}}$ is
${\mathcal{V}}$ is  $F$-prioritary and has
$F$-prioritary and has  $\operatorname{ch}{\mathcal{V}}=\mathbf{v}$.◻
$\operatorname{ch}{\mathcal{V}}=\mathbf{v}$.◻
By essentially the same proof, we can deduce that a general  ${\mathcal{V}}\in {\mathcal{P}}_{F}(\mathbf{v})$ splits as a balanced direct sum on the exceptional section
${\mathcal{V}}\in {\mathcal{P}}_{F}(\mathbf{v})$ splits as a balanced direct sum on the exceptional section  $E$.
$E$.
Corollary 3.6. Let  $\mathbf{v}\in K(\mathbb{F}_{e})$ be a character of positive rank with
$\mathbf{v}\in K(\mathbb{F}_{e})$ be a character of positive rank with  $\unicode[STIX]{x1D6E5}(\mathbf{v})\geqslant 0$. Then the general
$\unicode[STIX]{x1D6E5}(\mathbf{v})\geqslant 0$. Then the general  ${\mathcal{V}}\in {\mathcal{P}}_{F}(\mathbf{v})$ is
${\mathcal{V}}\in {\mathcal{P}}_{F}(\mathbf{v})$ is  $E$-prioritary, and furthermore
$E$-prioritary, and furthermore  ${\mathcal{V}}|_{E}$ is a balanced direct sum of line bundles.
${\mathcal{V}}|_{E}$ is a balanced direct sum of line bundles.
Proof. In the proof of Corollary 3.5, the bundle  ${\mathcal{W}}$ is
${\mathcal{W}}$ is  $E$-prioritary, and hence so is
$E$-prioritary, and hence so is  ${\mathcal{W}}(L)$. Then the sheaf
${\mathcal{W}}(L)$. Then the sheaf  ${\mathcal{V}}$ is also
${\mathcal{V}}$ is also  $E$-prioritary by Lemma 2.7. Furthermore,
$E$-prioritary by Lemma 2.7. Furthermore,  ${\mathcal{W}}|_{E}$ is clearly balanced, and hence so is
${\mathcal{W}}|_{E}$ is clearly balanced, and hence so is  ${\mathcal{W}}(L)|_{E}$ and
${\mathcal{W}}(L)|_{E}$ and  ${\mathcal{V}}|_{E}$. (Alternately, the balancedness of
${\mathcal{V}}|_{E}$. (Alternately, the balancedness of  ${\mathcal{V}}|_{E}$ follows from the general result Proposition 2.6.)◻
${\mathcal{V}}|_{E}$ follows from the general result Proposition 2.6.)◻
When further information about  $\mathbf{v}$ is known, the possibilities for the twisting line bundle
$\mathbf{v}$ is known, the possibilities for the twisting line bundle  $L$ such that
$L$ such that  $\mathbf{v}(-L)$ lies in
$\mathbf{v}(-L)$ lies in  $Q$ are restricted. This fact allows us to deduce further results about sheaves of character
$Q$ are restricted. This fact allows us to deduce further results about sheaves of character  $\mathbf{v}$.
$\mathbf{v}$.
Corollary 3.7. Let  $\mathbf{v}\in K(\mathbb{F}_{e})$ be a character of positive rank with
$\mathbf{v}\in K(\mathbb{F}_{e})$ be a character of positive rank with  $\unicode[STIX]{x1D6E5}(\mathbf{v})\geqslant 0$. Let
$\unicode[STIX]{x1D6E5}(\mathbf{v})\geqslant 0$. Let  ${\mathcal{V}}\in {\mathcal{P}}_{F}(\mathbf{v})$ be general.
${\mathcal{V}}\in {\mathcal{P}}_{F}(\mathbf{v})$ be general.
(1) If
 $\unicode[STIX]{x1D708}(\mathbf{v})\cdot F\geqslant -1$, then
$\unicode[STIX]{x1D708}(\mathbf{v})\cdot F\geqslant -1$, then  $h^{2}(\mathbb{F}_{e},{\mathcal{V}})=0$.
$h^{2}(\mathbb{F}_{e},{\mathcal{V}})=0$.(2) If
 $\unicode[STIX]{x1D708}(\mathbf{v})\cdot F\leqslant -1$, then
$\unicode[STIX]{x1D708}(\mathbf{v})\cdot F\leqslant -1$, then  $h^{0}(\mathbb{F}_{e},{\mathcal{V}})=0$.
$h^{0}(\mathbb{F}_{e},{\mathcal{V}})=0$.(3) In particular, if
 $\unicode[STIX]{x1D708}(\mathbf{v})\cdot F=-1$, then
$\unicode[STIX]{x1D708}(\mathbf{v})\cdot F=-1$, then  $h^{1}(\mathbb{F}_{e},{\mathcal{V}})=-\unicode[STIX]{x1D712}(\mathbf{v})$ and all other cohomology vanishes.
$h^{1}(\mathbb{F}_{e},{\mathcal{V}})=-\unicode[STIX]{x1D712}(\mathbf{v})$ and all other cohomology vanishes.(4) Suppose
 $\unicode[STIX]{x1D708}(\mathbf{v})\cdot F>-1$ and
$\unicode[STIX]{x1D708}(\mathbf{v})\cdot F>-1$ and  $\unicode[STIX]{x1D708}(\mathbf{v})\cdot E\geqslant -1$. Then
$\unicode[STIX]{x1D708}(\mathbf{v})\cdot E\geqslant -1$. Then  ${\mathcal{V}}$ has at most one nonzero cohomology group.
${\mathcal{V}}$ has at most one nonzero cohomology group.
Proof. (1) In the notation of the proof of Corollary 3.5, since  $\unicode[STIX]{x1D708}(\mathbf{v})\cdot F\geqslant -1$ we may assume the line bundle
$\unicode[STIX]{x1D708}(\mathbf{v})\cdot F\geqslant -1$ we may assume the line bundle  $L$ is of the form
$L$ is of the form  ${\mathcal{O}}_{\mathbb{F}_{e}}(aE+bF)$ with
${\mathcal{O}}_{\mathbb{F}_{e}}(aE+bF)$ with  $a\geqslant 0$ and
$a\geqslant 0$ and  $b\in \mathbb{Z}$. Then the line bundles appearing in
$b\in \mathbb{Z}$. Then the line bundles appearing in  ${\mathcal{W}}(L)$ (which are twists by
${\mathcal{W}}(L)$ (which are twists by  $L$ of the line bundles in the statement of Corollary 3.4) all clearly have no
$L$ of the line bundles in the statement of Corollary 3.4) all clearly have no  $h^{2}$. Then
$h^{2}$. Then  ${\mathcal{V}}$ also has no
${\mathcal{V}}$ also has no  $h^{2}$ by Lemma 2.7.
$h^{2}$ by Lemma 2.7.
(2) In this case, we may assume the line bundle  $L$ is of the form
$L$ is of the form  ${\mathcal{O}}_{\mathbb{F}_{e}}(aE+bF)$ with
${\mathcal{O}}_{\mathbb{F}_{e}}(aE+bF)$ with  $a\leqslant -1$ and
$a\leqslant -1$ and  $b\in \mathbb{Z}$. The line bundles appearing in
$b\in \mathbb{Z}$. The line bundles appearing in  ${\mathcal{W}}(L)$ all have no
${\mathcal{W}}(L)$ all have no  $h^{0}$. Then
$h^{0}$. Then  ${\mathcal{V}}$ is a subsheaf of
${\mathcal{V}}$ is a subsheaf of  ${\mathcal{W}}(L)$, so also has no
${\mathcal{W}}(L)$, so also has no  $h^{0}$.
$h^{0}$.
(3) This immediately follows from (1) and (2).
(4) This time we may assume the line bundle  $L$ is nef. Then by Theorem 2.1, the line bundles appearing in
$L$ is nef. Then by Theorem 2.1, the line bundles appearing in  ${\mathcal{W}}(L)$ all have no higher cohomology. By Lemma 2.7, performing general elementary modifications on
${\mathcal{W}}(L)$ all have no higher cohomology. By Lemma 2.7, performing general elementary modifications on  ${\mathcal{W}}(L)$ results in a bundle
${\mathcal{W}}(L)$ results in a bundle  ${\mathcal{V}}$ with at most one nonzero cohomology group.◻
${\mathcal{V}}$ with at most one nonzero cohomology group.◻
We can combine the last two corollaries to compute the Betti numbers of a general sheaf in the remaining cases. Together with the other results in this subsection, this completes the proof of Theorem 3.1.
Proposition 3.8. Let  $\mathbf{v}\in K(\mathbb{F}_{e})$ be a character of positive rank with
$\mathbf{v}\in K(\mathbb{F}_{e})$ be a character of positive rank with  $\unicode[STIX]{x1D6E5}(\mathbf{v})\geqslant 0$,
$\unicode[STIX]{x1D6E5}(\mathbf{v})\geqslant 0$,  $\unicode[STIX]{x1D708}(\mathbf{v})\cdot F>-1$ and
$\unicode[STIX]{x1D708}(\mathbf{v})\cdot F>-1$ and  $\unicode[STIX]{x1D708}(\mathbf{v})\cdot E<-1$. Let
$\unicode[STIX]{x1D708}(\mathbf{v})\cdot E<-1$. Let  ${\mathcal{V}}\in {\mathcal{P}}_{F}(\mathbf{v})$ be general. Then
${\mathcal{V}}\in {\mathcal{P}}_{F}(\mathbf{v})$ be general. Then  $H^{0}(\mathbb{F}_{e},{\mathcal{V}})\cong H^{0}(\mathbb{F}_{e},{\mathcal{V}}(-E))$, and the Betti numbers of
$H^{0}(\mathbb{F}_{e},{\mathcal{V}})\cong H^{0}(\mathbb{F}_{e},{\mathcal{V}}(-E))$, and the Betti numbers of  ${\mathcal{V}}$ can be determined inductively.
${\mathcal{V}}$ can be determined inductively.
Proof. Since  ${\mathcal{V}}|_{E}$ is balanced by Corollary 3.6 and
${\mathcal{V}}|_{E}$ is balanced by Corollary 3.6 and  $\unicode[STIX]{x1D708}(\mathbf{v})\cdot E<-1$, we conclude that
$\unicode[STIX]{x1D708}(\mathbf{v})\cdot E<-1$, we conclude that  $H^{0}(E,{\mathcal{V}}|_{E})=0$. Then the restriction sequence
$H^{0}(E,{\mathcal{V}}|_{E})=0$. Then the restriction sequence
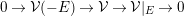 $$\begin{eqnarray}0\rightarrow {\mathcal{V}}(-E)\rightarrow {\mathcal{V}}\rightarrow {\mathcal{V}}|_{E}\rightarrow 0\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow {\mathcal{V}}(-E)\rightarrow {\mathcal{V}}\rightarrow {\mathcal{V}}|_{E}\rightarrow 0\end{eqnarray}$$ implies  $H^{0}(\mathbb{F}_{e},{\mathcal{V}})\cong H^{0}(\mathbb{F}_{e},{\mathcal{V}}(-E))$.
$H^{0}(\mathbb{F}_{e},{\mathcal{V}})\cong H^{0}(\mathbb{F}_{e},{\mathcal{V}}(-E))$.
It remains to explain how to compute the Betti numbers of  ${\mathcal{V}}$ inductively. Twisting
${\mathcal{V}}$ inductively. Twisting  ${\mathcal{V}}$ by
${\mathcal{V}}$ by  $-E$ has the effect of increasing
$-E$ has the effect of increasing  $\unicode[STIX]{x1D708}(\mathbf{v})\cdot E$ by
$\unicode[STIX]{x1D708}(\mathbf{v})\cdot E$ by  $e$ and decreasing
$e$ and decreasing  $\unicode[STIX]{x1D708}(\mathbf{v})\cdot F$ by
$\unicode[STIX]{x1D708}(\mathbf{v})\cdot F$ by  $1$. Hence there is a smallest integer
$1$. Hence there is a smallest integer  $m\geqslant 1$ such that either
$m\geqslant 1$ such that either  $\unicode[STIX]{x1D708}(\mathbf{v}(-mE))\cdot E\geqslant -1$ or
$\unicode[STIX]{x1D708}(\mathbf{v}(-mE))\cdot E\geqslant -1$ or  $\unicode[STIX]{x1D708}(\mathbf{v}(-mE))\cdot F\leqslant -1$, and by induction we find
$\unicode[STIX]{x1D708}(\mathbf{v}(-mE))\cdot F\leqslant -1$, and by induction we find  $h^{0}(\mathbb{F}_{e},{\mathcal{V}})=h^{0}(\mathbb{F}_{e},{\mathcal{V}}(-mE))$.
$h^{0}(\mathbb{F}_{e},{\mathcal{V}})=h^{0}(\mathbb{F}_{e},{\mathcal{V}}(-mE))$.
If  $\unicode[STIX]{x1D708}(\mathbf{v}(-mE))\cdot F\leqslant -1$, Corollary 3.7 gives
$\unicode[STIX]{x1D708}(\mathbf{v}(-mE))\cdot F\leqslant -1$, Corollary 3.7 gives  $h^{0}(\mathbb{F}_{e},{\mathcal{V}})=h^{2}(\mathbb{F}_{e},{\mathcal{V}})=0$, and so
$h^{0}(\mathbb{F}_{e},{\mathcal{V}})=h^{2}(\mathbb{F}_{e},{\mathcal{V}})=0$, and so  $h^{1}(\mathbb{F}_{e},{\mathcal{V}})=-\unicode[STIX]{x1D712}(\mathbf{v})$.
$h^{1}(\mathbb{F}_{e},{\mathcal{V}})=-\unicode[STIX]{x1D712}(\mathbf{v})$.
On the other hand if  $\unicode[STIX]{x1D708}(\mathbf{v}(-mE))\cdot F>-1$, then
$\unicode[STIX]{x1D708}(\mathbf{v}(-mE))\cdot F>-1$, then  $\unicode[STIX]{x1D708}(\mathbf{v}(-mE))\cdot E\geqslant -1$. Corollary 3.7 gives
$\unicode[STIX]{x1D708}(\mathbf{v}(-mE))\cdot E\geqslant -1$. Corollary 3.7 gives  $h^{0}(\mathbb{F}_{e},{\mathcal{V}})=\max \{\unicode[STIX]{x1D712}(\mathbf{v}(-mE)),0\}$ and
$h^{0}(\mathbb{F}_{e},{\mathcal{V}})=\max \{\unicode[STIX]{x1D712}(\mathbf{v}(-mE)),0\}$ and  $h^{2}(\mathbb{F}_{e},{\mathcal{V}})=0$, and
$h^{2}(\mathbb{F}_{e},{\mathcal{V}})=0$, and  $h^{1}(\mathbb{F}_{e},{\mathcal{V}})$ is determined by Riemann–Roch. Note that in this case
$h^{1}(\mathbb{F}_{e},{\mathcal{V}})$ is determined by Riemann–Roch. Note that in this case  $h^{1}(\mathbb{F}_{e},{\mathcal{V}})$ is always nonzero. Indeed, since
$h^{1}(\mathbb{F}_{e},{\mathcal{V}})$ is always nonzero. Indeed, since  $m\geqslant 1$, we find
$m\geqslant 1$, we find  $\unicode[STIX]{x1D708}(\mathbf{v}(-E))\cdot F>-1$. By Corollary 3.7, we have
$\unicode[STIX]{x1D708}(\mathbf{v}(-E))\cdot F>-1$. By Corollary 3.7, we have  $h^{2}(\mathbb{F}_{e},{\mathcal{V}}(-E))=0$. Then
$h^{2}(\mathbb{F}_{e},{\mathcal{V}}(-E))=0$. Then  $H^{1}(\mathbb{F}_{e},{\mathcal{V}})\rightarrow H^{1}(\mathbb{F}_{e},{\mathcal{V}}|_{E})$ is surjective, and
$H^{1}(\mathbb{F}_{e},{\mathcal{V}})\rightarrow H^{1}(\mathbb{F}_{e},{\mathcal{V}}|_{E})$ is surjective, and  $h^{1}(\mathbb{F}_{e},{\mathcal{V}}|_{E})>0$ since
$h^{1}(\mathbb{F}_{e},{\mathcal{V}}|_{E})>0$ since  $\unicode[STIX]{x1D708}(\mathbf{v})\cdot E<-1$.◻
$\unicode[STIX]{x1D708}(\mathbf{v})\cdot E<-1$.◻
3.3 The Brill–Noether theorem
We call a character  $\mathbf{v}\in K(\mathbb{F}_{e})$ of positive rank special if the general sheaf
$\mathbf{v}\in K(\mathbb{F}_{e})$ of positive rank special if the general sheaf  ${\mathcal{V}}\in {\mathcal{P}}_{F}(\mathbf{v})$ has more than one nonzero cohomology group, and nonspecial otherwise. It is useful for applications to convert the statement of Theorem 3.1 to a classification of the nonspecial characters. Again we concentrate on the case
${\mathcal{V}}\in {\mathcal{P}}_{F}(\mathbf{v})$ has more than one nonzero cohomology group, and nonspecial otherwise. It is useful for applications to convert the statement of Theorem 3.1 to a classification of the nonspecial characters. Again we concentrate on the case  $\unicode[STIX]{x1D708}(\mathbf{v})\cdot F\geqslant -1$ and rely on Serre duality otherwise.
$\unicode[STIX]{x1D708}(\mathbf{v})\cdot F\geqslant -1$ and rely on Serre duality otherwise.
Corollary 3.9. Let  $\mathbf{v}\in K(\mathbb{F}_{e})$ be a character with positive rank and
$\mathbf{v}\in K(\mathbb{F}_{e})$ be a character with positive rank and  $\unicode[STIX]{x1D6E5}(\mathbf{v})\geqslant 0$, and suppose
$\unicode[STIX]{x1D6E5}(\mathbf{v})\geqslant 0$, and suppose  $\unicode[STIX]{x1D708}(\mathbf{v})\cdot F\geqslant -1$. Then
$\unicode[STIX]{x1D708}(\mathbf{v})\cdot F\geqslant -1$. Then  $\mathbf{v}$ is nonspecial if and only if one of the following holds.
$\mathbf{v}$ is nonspecial if and only if one of the following holds.
(1) We have
 $\unicode[STIX]{x1D708}(\mathbf{v})\cdot F=-1$.
$\unicode[STIX]{x1D708}(\mathbf{v})\cdot F=-1$.(2) We have
 $\unicode[STIX]{x1D708}(\mathbf{v})\cdot F>-1$ and
$\unicode[STIX]{x1D708}(\mathbf{v})\cdot F>-1$ and  $\unicode[STIX]{x1D708}(\mathbf{v})\cdot E\geqslant -1$.
$\unicode[STIX]{x1D708}(\mathbf{v})\cdot E\geqslant -1$.(3) If
 $\unicode[STIX]{x1D708}(\mathbf{v})\cdot F>-1$ and
$\unicode[STIX]{x1D708}(\mathbf{v})\cdot F>-1$ and  $\unicode[STIX]{x1D708}(\mathbf{v})\cdot E<-1$, let
$\unicode[STIX]{x1D708}(\mathbf{v})\cdot E<-1$, let  $m$ be the smallest positive integer such that either
$m$ be the smallest positive integer such that either  $\unicode[STIX]{x1D708}(\mathbf{v}(-mE))\cdot F\leqslant -1$ or
$\unicode[STIX]{x1D708}(\mathbf{v}(-mE))\cdot F\leqslant -1$ or  $\unicode[STIX]{x1D708}(\mathbf{v}(-mE))\cdot E\geqslant -1$.
$\unicode[STIX]{x1D708}(\mathbf{v}(-mE))\cdot E\geqslant -1$.(a) If
 $\unicode[STIX]{x1D708}(\mathbf{v}(-mE))\cdot F\leqslant -1$, then
$\unicode[STIX]{x1D708}(\mathbf{v}(-mE))\cdot F\leqslant -1$, then  $\mathbf{v}$ is nonspecial.
$\mathbf{v}$ is nonspecial.(b) If
 $\unicode[STIX]{x1D708}(\mathbf{v}(-mE))\cdot F>-1$, then
$\unicode[STIX]{x1D708}(\mathbf{v}(-mE))\cdot F>-1$, then  $\mathbf{v}$ is nonspecial if and only if
$\mathbf{v}$ is nonspecial if and only if  $\unicode[STIX]{x1D712}(\mathbf{v}(-mE))\leqslant 0$.
$\unicode[STIX]{x1D712}(\mathbf{v}(-mE))\leqslant 0$.
Proof. Theorem 3.1 shows  $\mathbf{v}$ is nonspecial if we are in case (1) or (2). In case (3), the proof of Proposition 3.8 shows
$\mathbf{v}$ is nonspecial if we are in case (1) or (2). In case (3), the proof of Proposition 3.8 shows  $\mathbf{v}$ is nonspecial if and only if the listed conditions are satisfied.◻
$\mathbf{v}$ is nonspecial if and only if the listed conditions are satisfied.◻
It is worth pointing out that when  $\unicode[STIX]{x1D712}(\mathbf{v})\geqslant 0$, then case (3) in Corollary 3.9 does not occur, so that the classification takes a particularly simple form.
$\unicode[STIX]{x1D712}(\mathbf{v})\geqslant 0$, then case (3) in Corollary 3.9 does not occur, so that the classification takes a particularly simple form.
Corollary 3.10. Let  $\mathbf{v}\in K(\mathbb{F}_{e})$ be a character with positive rank and
$\mathbf{v}\in K(\mathbb{F}_{e})$ be a character with positive rank and  $\unicode[STIX]{x1D6E5}(\mathbf{v})\geqslant 0$, and suppose
$\unicode[STIX]{x1D6E5}(\mathbf{v})\geqslant 0$, and suppose  $\unicode[STIX]{x1D708}(\mathbf{v})\cdot F\geqslant -1$ and
$\unicode[STIX]{x1D708}(\mathbf{v})\cdot F\geqslant -1$ and  $\unicode[STIX]{x1D712}(\mathbf{v})\geqslant 0$. Then
$\unicode[STIX]{x1D712}(\mathbf{v})\geqslant 0$. Then  $\mathbf{v}$ is nonspecial if and only if one of the following holds.
$\mathbf{v}$ is nonspecial if and only if one of the following holds.
(1) We have
 $\unicode[STIX]{x1D708}(\mathbf{v})\cdot F=-1$.
$\unicode[STIX]{x1D708}(\mathbf{v})\cdot F=-1$.(2) We have
 $\unicode[STIX]{x1D708}(\mathbf{v})\cdot F>-1$ and
$\unicode[STIX]{x1D708}(\mathbf{v})\cdot F>-1$ and  $\unicode[STIX]{x1D708}(\mathbf{v})\cdot E\geqslant -1$.
$\unicode[STIX]{x1D708}(\mathbf{v})\cdot E\geqslant -1$.
Proof. Let  ${\mathcal{V}}\in {\mathcal{P}}_{F}(\mathbf{v})$ be general. Assume
${\mathcal{V}}\in {\mathcal{P}}_{F}(\mathbf{v})$ be general. Assume  $\unicode[STIX]{x1D708}(\mathbf{v})\cdot F>-1$ and
$\unicode[STIX]{x1D708}(\mathbf{v})\cdot F>-1$ and  $\unicode[STIX]{x1D708}(\mathbf{v})\cdot E<-1$; we must show
$\unicode[STIX]{x1D708}(\mathbf{v})\cdot E<-1$; we must show  $\mathbf{v}$ is special. Since
$\mathbf{v}$ is special. Since  $\unicode[STIX]{x1D712}(\mathbf{v})\geqslant 0$, it will suffice to show
$\unicode[STIX]{x1D712}(\mathbf{v})\geqslant 0$, it will suffice to show  $h^{1}(\mathbb{F}_{e},{\mathcal{V}})$ is nonzero.
$h^{1}(\mathbb{F}_{e},{\mathcal{V}})$ is nonzero.
The inequality  $\unicode[STIX]{x1D708}(\mathbf{v})\cdot E<-1$ gives
$\unicode[STIX]{x1D708}(\mathbf{v})\cdot E<-1$ gives  $h^{1}(E,{\mathcal{V}}|_{E})\neq 0$, so if
$h^{1}(E,{\mathcal{V}}|_{E})\neq 0$, so if  $h^{2}(\mathbb{F}_{e},{\mathcal{V}}(-E))=0$, then the surjection
$h^{2}(\mathbb{F}_{e},{\mathcal{V}}(-E))=0$, then the surjection  $H^{1}(\mathbb{F}_{e},{\mathcal{V}})\rightarrow H^{1}(E,{\mathcal{V}}|_{E})$ shows
$H^{1}(\mathbb{F}_{e},{\mathcal{V}})\rightarrow H^{1}(E,{\mathcal{V}}|_{E})$ shows  $h^{1}(\mathbb{F}_{e},{\mathcal{V}})\neq 0$. Now if
$h^{1}(\mathbb{F}_{e},{\mathcal{V}})\neq 0$. Now if  $\unicode[STIX]{x1D708}(\mathbf{v})\cdot F\geqslant 0$, then
$\unicode[STIX]{x1D708}(\mathbf{v})\cdot F\geqslant 0$, then  $\unicode[STIX]{x1D708}(\mathbf{v}(-E))\cdot F\geqslant -1$ and
$\unicode[STIX]{x1D708}(\mathbf{v}(-E))\cdot F\geqslant -1$ and  $h^{2}(\mathbb{F}_{e},{\mathcal{V}}(-E))=0$ follows from Theorem 3.1, completing the proof in this case.
$h^{2}(\mathbb{F}_{e},{\mathcal{V}}(-E))=0$ follows from Theorem 3.1, completing the proof in this case.
If instead  $-1<\unicode[STIX]{x1D708}(\mathbf{v})\cdot F<0$, then the assumptions
$-1<\unicode[STIX]{x1D708}(\mathbf{v})\cdot F<0$, then the assumptions  $\unicode[STIX]{x1D712}(\mathbf{v})\geqslant 0$, and
$\unicode[STIX]{x1D712}(\mathbf{v})\geqslant 0$, and  $\unicode[STIX]{x1D6E5}(\mathbf{v})\geqslant 0$ together imply
$\unicode[STIX]{x1D6E5}(\mathbf{v})\geqslant 0$ together imply  $\unicode[STIX]{x1D708}(\mathbf{v})\cdot E\geqslant -1$, contradicting our assumption. Indeed, write
$\unicode[STIX]{x1D708}(\mathbf{v})\cdot E\geqslant -1$, contradicting our assumption. Indeed, write  $\unicode[STIX]{x1D708}(\mathbf{v})=(k/r)E+(l/r)F$. By the Riemann–Roch formula,
$\unicode[STIX]{x1D708}(\mathbf{v})=(k/r)E+(l/r)F$. By the Riemann–Roch formula,
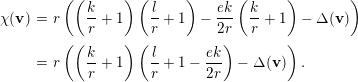 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D712}(\mathbf{v}) & = & \displaystyle r\left(\left(\frac{k}{r}+1\right)\left(\frac{l}{r}+1\right)-\frac{ek}{2r}\left(\frac{k}{r}+1\right)-\unicode[STIX]{x1D6E5}(\mathbf{v})\right)\nonumber\\ \displaystyle & = & \displaystyle r\left(\left(\frac{k}{r}+1\right)\left(\frac{l}{r}+1-\frac{ek}{2r}\right)-\unicode[STIX]{x1D6E5}(\mathbf{v})\right).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D712}(\mathbf{v}) & = & \displaystyle r\left(\left(\frac{k}{r}+1\right)\left(\frac{l}{r}+1\right)-\frac{ek}{2r}\left(\frac{k}{r}+1\right)-\unicode[STIX]{x1D6E5}(\mathbf{v})\right)\nonumber\\ \displaystyle & = & \displaystyle r\left(\left(\frac{k}{r}+1\right)\left(\frac{l}{r}+1-\frac{ek}{2r}\right)-\unicode[STIX]{x1D6E5}(\mathbf{v})\right).\nonumber\end{eqnarray}$$ Then  $\unicode[STIX]{x1D708}(\mathbf{v})\cdot F=k/r$, so our assumptions
$\unicode[STIX]{x1D708}(\mathbf{v})\cdot F=k/r$, so our assumptions  $\unicode[STIX]{x1D708}(\mathbf{v})\cdot F>-1$,
$\unicode[STIX]{x1D708}(\mathbf{v})\cdot F>-1$,  $\unicode[STIX]{x1D6E5}(\mathbf{v})\geqslant 0$, and
$\unicode[STIX]{x1D6E5}(\mathbf{v})\geqslant 0$, and  $\unicode[STIX]{x1D712}(\mathbf{v})\geqslant 0$ imply
$\unicode[STIX]{x1D712}(\mathbf{v})\geqslant 0$ imply  $l/r\geqslant -1+ek/2r$. Hence,
$l/r\geqslant -1+ek/2r$. Hence,
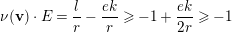 $$\begin{eqnarray}\unicode[STIX]{x1D708}(\mathbf{v})\cdot E=\frac{l}{r}-\frac{ek}{r}\geqslant -1+\frac{ek}{2r}\geqslant -1\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D708}(\mathbf{v})\cdot E=\frac{l}{r}-\frac{ek}{r}\geqslant -1+\frac{ek}{2r}\geqslant -1\end{eqnarray}$$ since  $k/r=\unicode[STIX]{x1D708}(\mathbf{v})\cdot F<0$. Thus this case never arises.◻
$k/r=\unicode[STIX]{x1D708}(\mathbf{v})\cdot F<0$. Thus this case never arises.◻
4 Gaeta-type resolutions
In this section, we study resolutions of sheaves on  $\mathbb{F}_{e}$ analogous to the Gaeta resolution of general sheaves on
$\mathbb{F}_{e}$ analogous to the Gaeta resolution of general sheaves on  $\mathbb{P}^{2}$. Families of such resolutions give unirational parameterizations of moduli spaces of sheaves, and so give an important tool for studying general sheaves.
$\mathbb{P}^{2}$. Families of such resolutions give unirational parameterizations of moduli spaces of sheaves, and so give an important tool for studying general sheaves.
Definition 4.1. Let  $L$ be a line bundle on
$L$ be a line bundle on  $\mathbb{F}_{e}$. An
$\mathbb{F}_{e}$. An  $L$-Gaeta-type resolution of a sheaf
$L$-Gaeta-type resolution of a sheaf  ${\mathcal{V}}$ on
${\mathcal{V}}$ on  $\mathbb{F}_{e}$ is a resolution of
$\mathbb{F}_{e}$ is a resolution of  ${\mathcal{V}}$ of the form
${\mathcal{V}}$ of the form
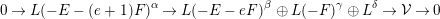 $$\begin{eqnarray}0\rightarrow L(-E-(e+1)F)^{\unicode[STIX]{x1D6FC}}\rightarrow L(-E-eF)^{\unicode[STIX]{x1D6FD}}\oplus L(-F)^{\unicode[STIX]{x1D6FE}}\oplus L^{\unicode[STIX]{x1D6FF}}\rightarrow {\mathcal{V}}\rightarrow 0\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow L(-E-(e+1)F)^{\unicode[STIX]{x1D6FC}}\rightarrow L(-E-eF)^{\unicode[STIX]{x1D6FD}}\oplus L(-F)^{\unicode[STIX]{x1D6FE}}\oplus L^{\unicode[STIX]{x1D6FF}}\rightarrow {\mathcal{V}}\rightarrow 0\end{eqnarray}$$ where  $\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FF}$ are nonnegative integers. We say a sheaf
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FF}$ are nonnegative integers. We say a sheaf  ${\mathcal{V}}$ has a Gaeta-type resolution if it admits an
${\mathcal{V}}$ has a Gaeta-type resolution if it admits an  $L$-Gaeta-type resolution for some line bundle
$L$-Gaeta-type resolution for some line bundle  $L$.
$L$.
Our main result in this section constructs Gaeta-type resolutions of general prioritary sheaves  ${\mathcal{V}}\in {\mathcal{P}}_{F}(\mathbf{v})$ on
${\mathcal{V}}\in {\mathcal{P}}_{F}(\mathbf{v})$ on  $\mathbb{F}_{e}$ under mild assumptions on
$\mathbb{F}_{e}$ under mild assumptions on  $\mathbf{v}$.
$\mathbf{v}$.
Theorem 4.2. Let  $\mathbf{v}\in K(\mathbb{F}_{e})$ be a Chern character of positive rank, and assume
$\mathbf{v}\in K(\mathbb{F}_{e})$ be a Chern character of positive rank, and assume
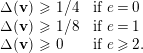 $$\begin{eqnarray}\begin{array}{@{}rcll@{}}\unicode[STIX]{x1D6E5}(\mathbf{v})\ & {\geqslant}\ & 1/4 & \text{if }e=0\\ \unicode[STIX]{x1D6E5}(\mathbf{v})\ & {\geqslant}\ & 1/8 & \text{if }e=1\\ \unicode[STIX]{x1D6E5}(\mathbf{v})\ & {\geqslant}\ & 0 & \text{if }e\geqslant 2.\end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}rcll@{}}\unicode[STIX]{x1D6E5}(\mathbf{v})\ & {\geqslant}\ & 1/4 & \text{if }e=0\\ \unicode[STIX]{x1D6E5}(\mathbf{v})\ & {\geqslant}\ & 1/8 & \text{if }e=1\\ \unicode[STIX]{x1D6E5}(\mathbf{v})\ & {\geqslant}\ & 0 & \text{if }e\geqslant 2.\end{array}\end{eqnarray}$$ Let  ${\mathcal{V}}\in {\mathcal{P}}_{F}(\mathbf{v})$ be a general prioritary sheaf. Then
${\mathcal{V}}\in {\mathcal{P}}_{F}(\mathbf{v})$ be a general prioritary sheaf. Then  ${\mathcal{V}}$ admits a Gaeta-type resolution.
${\mathcal{V}}$ admits a Gaeta-type resolution.
In particular, if there are  $\unicode[STIX]{x1D707}_{H}$-semistable sheaves of character
$\unicode[STIX]{x1D707}_{H}$-semistable sheaves of character  $\mathbf{v}$, the same result holds for a general
$\mathbf{v}$, the same result holds for a general  ${\mathcal{V}}\in M_{H}^{\unicode[STIX]{x1D707}\text{-}\mathit{ss}}(\mathbf{v})$.
${\mathcal{V}}\in M_{H}^{\unicode[STIX]{x1D707}\text{-}\mathit{ss}}(\mathbf{v})$.
First we observe that if a sheaf  ${\mathcal{V}}$ admits an
${\mathcal{V}}$ admits an  $L$-Gaeta-type resolution, then the exponents in the resolution are determined by
$L$-Gaeta-type resolution, then the exponents in the resolution are determined by  $\mathbf{v}=\operatorname{ch}{\mathcal{V}}$, and they are easily computable.
$\mathbf{v}=\operatorname{ch}{\mathcal{V}}$, and they are easily computable.
Lemma 4.3. Suppose  ${\mathcal{V}}$ is a sheaf on
${\mathcal{V}}$ is a sheaf on  $\mathbb{F}_{e}$ with an
$\mathbb{F}_{e}$ with an  $L$-Gaeta-type resolution
$L$-Gaeta-type resolution
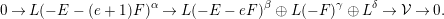 $$\begin{eqnarray}0\rightarrow L(-E-(e+1)F)^{\unicode[STIX]{x1D6FC}}\rightarrow L(-E-eF)^{\unicode[STIX]{x1D6FD}}\oplus L(-F)^{\unicode[STIX]{x1D6FE}}\oplus L^{\unicode[STIX]{x1D6FF}}\rightarrow {\mathcal{V}}\rightarrow 0.\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow L(-E-(e+1)F)^{\unicode[STIX]{x1D6FC}}\rightarrow L(-E-eF)^{\unicode[STIX]{x1D6FD}}\oplus L(-F)^{\unicode[STIX]{x1D6FE}}\oplus L^{\unicode[STIX]{x1D6FF}}\rightarrow {\mathcal{V}}\rightarrow 0.\end{eqnarray}$$ Then the exponents  $\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FF}$ are the integers
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FF}$ are the integers
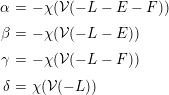 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FC} & = & \displaystyle -\unicode[STIX]{x1D712}({\mathcal{V}}(-L-E-F))\nonumber\\ \displaystyle \unicode[STIX]{x1D6FD} & = & \displaystyle -\unicode[STIX]{x1D712}({\mathcal{V}}(-L-E))\nonumber\\ \displaystyle \unicode[STIX]{x1D6FE} & = & \displaystyle -\unicode[STIX]{x1D712}({\mathcal{V}}(-L-F))\nonumber\\ \displaystyle \unicode[STIX]{x1D6FF} & = & \displaystyle \unicode[STIX]{x1D712}({\mathcal{V}}(-L))\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FC} & = & \displaystyle -\unicode[STIX]{x1D712}({\mathcal{V}}(-L-E-F))\nonumber\\ \displaystyle \unicode[STIX]{x1D6FD} & = & \displaystyle -\unicode[STIX]{x1D712}({\mathcal{V}}(-L-E))\nonumber\\ \displaystyle \unicode[STIX]{x1D6FE} & = & \displaystyle -\unicode[STIX]{x1D712}({\mathcal{V}}(-L-F))\nonumber\\ \displaystyle \unicode[STIX]{x1D6FF} & = & \displaystyle \unicode[STIX]{x1D712}({\mathcal{V}}(-L))\nonumber\end{eqnarray}$$ which depend only on  $\mathbf{v}=\operatorname{ch}{\mathcal{V}}$. In particular,
$\mathbf{v}=\operatorname{ch}{\mathcal{V}}$. In particular,  $L$ must be a line bundle such that the inequalities
$L$ must be a line bundle such that the inequalities
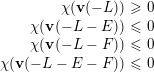
are satisfied.
Proof. For example, to establish the equality  $\unicode[STIX]{x1D6FC}=-\unicode[STIX]{x1D712}({\mathcal{V}}(-L-E-F))$ we tensor the resolution of
$\unicode[STIX]{x1D6FC}=-\unicode[STIX]{x1D712}({\mathcal{V}}(-L-E-F))$ we tensor the resolution of  ${\mathcal{V}}$ by
${\mathcal{V}}$ by  ${\mathcal{O}}_{\mathbb{F}_{e}}(-L-E-F)$ and use the additivity of the Euler characteristic and Riemann–Roch for line bundles to find
${\mathcal{O}}_{\mathbb{F}_{e}}(-L-E-F)$ and use the additivity of the Euler characteristic and Riemann–Roch for line bundles to find
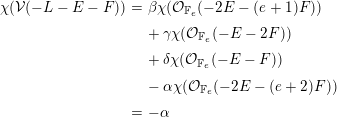 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D712}({\mathcal{V}}(-L-E-F)) & = & \displaystyle \unicode[STIX]{x1D6FD}\unicode[STIX]{x1D712}({\mathcal{O}}_{\mathbb{F}_{e}}(-2E-(e+1)F))\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D712}({\mathcal{O}}_{\mathbb{F}_{e}}(-E-2F))\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D712}({\mathcal{O}}_{\mathbb{F}_{e}}(-E-F))\nonumber\\ \displaystyle & & \displaystyle -\,\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D712}({\mathcal{O}}_{\mathbb{F}_{e}}(-2E-(e+2)F))\nonumber\\ \displaystyle & = & \displaystyle -\unicode[STIX]{x1D6FC}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D712}({\mathcal{V}}(-L-E-F)) & = & \displaystyle \unicode[STIX]{x1D6FD}\unicode[STIX]{x1D712}({\mathcal{O}}_{\mathbb{F}_{e}}(-2E-(e+1)F))\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D712}({\mathcal{O}}_{\mathbb{F}_{e}}(-E-2F))\nonumber\\ \displaystyle & & \displaystyle +\,\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D712}({\mathcal{O}}_{\mathbb{F}_{e}}(-E-F))\nonumber\\ \displaystyle & & \displaystyle -\,\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D712}({\mathcal{O}}_{\mathbb{F}_{e}}(-2E-(e+2)F))\nonumber\\ \displaystyle & = & \displaystyle -\unicode[STIX]{x1D6FC}\nonumber\end{eqnarray}$$The other equalities are proved in the same way. ◻
Conversely, if a line bundle  $L$ can be found such that the numerical inequalities (
$L$ can be found such that the numerical inequalities ( $\dagger$) are satisfied, then the next result shows that general sheaves admit
$\dagger$) are satisfied, then the next result shows that general sheaves admit  $L$-Gaeta-type resolutions. Thus the problem of constructing Gaeta-type resolutions is reduced to the numerical problem of finding a line bundle
$L$-Gaeta-type resolutions. Thus the problem of constructing Gaeta-type resolutions is reduced to the numerical problem of finding a line bundle  $L$ satisfying the inequalities (
$L$ satisfying the inequalities ( $\dagger$).
$\dagger$).
Proposition 4.4. Suppose  $\mathbf{v}\in K(\mathbb{F}_{e})$ is a Chern character of positive rank and there is a line bundle
$\mathbf{v}\in K(\mathbb{F}_{e})$ is a Chern character of positive rank and there is a line bundle  $L$ such that the inequalities (
$L$ such that the inequalities ( $\dagger$) are satisfied. Then
$\dagger$) are satisfied. Then  ${\mathcal{P}}_{F}(\mathbf{v})$ is nonempty and a general
${\mathcal{P}}_{F}(\mathbf{v})$ is nonempty and a general  ${\mathcal{V}}\in {\mathcal{P}}_{F}(\mathbf{v})$ admits an
${\mathcal{V}}\in {\mathcal{P}}_{F}(\mathbf{v})$ admits an  $L$-Gaeta-type resolution.
$L$-Gaeta-type resolution.
Proof. Define positive integers  $\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FF}$ as in the statement of Lemma 4.3 and define
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FF}$ as in the statement of Lemma 4.3 and define
 $$\begin{eqnarray}A=L(-E-(e+1)F)^{\unicode[STIX]{x1D6FC}}\qquad B=L(-E-eF)^{\unicode[STIX]{x1D6FD}}\oplus L(-F)^{\unicode[STIX]{x1D6FE}}\oplus L^{\unicode[STIX]{x1D6FF}}.\end{eqnarray}$$
$$\begin{eqnarray}A=L(-E-(e+1)F)^{\unicode[STIX]{x1D6FC}}\qquad B=L(-E-eF)^{\unicode[STIX]{x1D6FD}}\oplus L(-F)^{\unicode[STIX]{x1D6FE}}\oplus L^{\unicode[STIX]{x1D6FF}}.\end{eqnarray}$$ Then any complex  $A\stackrel{\unicode[STIX]{x1D719}}{\rightarrow }B$ sitting in degrees
$A\stackrel{\unicode[STIX]{x1D719}}{\rightarrow }B$ sitting in degrees  $-1$ and
$-1$ and  $0$ has Chern character
$0$ has Chern character  $\mathbf{v}$. Indeed,
$\mathbf{v}$. Indeed,  $K(\mathbb{F}_{e})\otimes \mathbb{Q}$ has a basis given by the four line bundles
$K(\mathbb{F}_{e})\otimes \mathbb{Q}$ has a basis given by the four line bundles
 $$\begin{eqnarray}-L-E-F,-L-E,-L-F,-L.\end{eqnarray}$$
$$\begin{eqnarray}-L-E-F,-L-E,-L-F,-L.\end{eqnarray}$$ If  $\mathbf{w}$ is the character of the complex
$\mathbf{w}$ is the character of the complex  $A\stackrel{\unicode[STIX]{x1D719}}{\rightarrow }B$, then by the choice of the integers
$A\stackrel{\unicode[STIX]{x1D719}}{\rightarrow }B$, then by the choice of the integers  $\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FF}$ we find that
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE},\unicode[STIX]{x1D6FF}$ we find that  $\mathbf{v}-\mathbf{w}$ is orthogonal to each of these four line bundles under the Euler pairing
$\mathbf{v}-\mathbf{w}$ is orthogonal to each of these four line bundles under the Euler pairing  $(\mathbf{u},\mathbf{u}^{\prime })=\unicode[STIX]{x1D712}(\mathbf{u}\otimes \mathbf{u}^{\prime })$. Since the Euler pairing is nondegenerate,
$(\mathbf{u},\mathbf{u}^{\prime })=\unicode[STIX]{x1D712}(\mathbf{u}\otimes \mathbf{u}^{\prime })$. Since the Euler pairing is nondegenerate,  $\mathbf{v}=\mathbf{w}$. In particular, the rank of the complex
$\mathbf{v}=\mathbf{w}$. In particular, the rank of the complex  $r(B)-r(A)=r(\mathbf{v})$ is positive.
$r(B)-r(A)=r(\mathbf{v})$ is positive.
Let  $U\subset \operatorname{Hom}(A,B)$ be the open subset parameterizing injective sheaf maps
$U\subset \operatorname{Hom}(A,B)$ be the open subset parameterizing injective sheaf maps  $\unicode[STIX]{x1D719}$ with torsion-free cokernel
$\unicode[STIX]{x1D719}$ with torsion-free cokernel  ${\mathcal{V}}_{\unicode[STIX]{x1D719}}$. We check the hypotheses (1)–(3) of Theorem 2.10. Note that each of the line bundles
${\mathcal{V}}_{\unicode[STIX]{x1D719}}$. We check the hypotheses (1)–(3) of Theorem 2.10. Note that each of the line bundles
 $$\begin{eqnarray}\displaystyle {\mathcal{H}}\mathit{om}(L(-E-(e+1)F),L(-E-eF)) & = & \displaystyle {\mathcal{O}}_{\mathbb{F}_{e}}(F)\nonumber\\ \displaystyle {\mathcal{H}}\mathit{om}(L(-E-(e+1)F),L(-F)) & = & \displaystyle {\mathcal{O}}_{\mathbb{F}_{e}}(E+eF)\nonumber\\ \displaystyle {\mathcal{H}}\mathit{om}(L(-E-(e+1)F),L) & = & \displaystyle {\mathcal{O}}_{\mathbb{F}_{e}}(E+(e+1)F)\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle {\mathcal{H}}\mathit{om}(L(-E-(e+1)F),L(-E-eF)) & = & \displaystyle {\mathcal{O}}_{\mathbb{F}_{e}}(F)\nonumber\\ \displaystyle {\mathcal{H}}\mathit{om}(L(-E-(e+1)F),L(-F)) & = & \displaystyle {\mathcal{O}}_{\mathbb{F}_{e}}(E+eF)\nonumber\\ \displaystyle {\mathcal{H}}\mathit{om}(L(-E-(e+1)F),L) & = & \displaystyle {\mathcal{O}}_{\mathbb{F}_{e}}(E+(e+1)F)\nonumber\end{eqnarray}$$ are globally generated. The vanishings  $\operatorname{Ext}^{1}(A,B(-F))=0$ and
$\operatorname{Ext}^{1}(A,B(-F))=0$ and  $\operatorname{Ext}^{2}(B,B(-F))$ both follow immediately from Theorem 2.1. We already saw
$\operatorname{Ext}^{2}(B,B(-F))$ both follow immediately from Theorem 2.1. We already saw  $r(B)-r(A)>0$. Thus the hypotheses of Theorem 2.10 are satisfied, and
$r(B)-r(A)>0$. Thus the hypotheses of Theorem 2.10 are satisfied, and  ${\mathcal{V}}_{\unicode[STIX]{x1D719}}/U$ is a nonempty complete family of
${\mathcal{V}}_{\unicode[STIX]{x1D719}}/U$ is a nonempty complete family of  $F$-prioritary sheaves which admit
$F$-prioritary sheaves which admit  $L$-Gaeta-type resolutions. Since
$L$-Gaeta-type resolutions. Since  ${\mathcal{P}}_{F}(\mathbf{v})$ is irreducible, this completes the proof.◻
${\mathcal{P}}_{F}(\mathbf{v})$ is irreducible, this completes the proof.◻
Finally we show that under the assumptions on  $\unicode[STIX]{x1D6E5}(\mathbf{v})$ in Theorem 4.2 it is possible to find a suitable line bundle
$\unicode[STIX]{x1D6E5}(\mathbf{v})$ in Theorem 4.2 it is possible to find a suitable line bundle  $L$. Together with Proposition 4.4, the next result completes the proof of Theorem 4.2.
$L$. Together with Proposition 4.4, the next result completes the proof of Theorem 4.2.
Lemma 4.5. Let  $\mathbf{v}\in K(\mathbb{F}_{e})$ be a Chern character of positive rank, and assume
$\mathbf{v}\in K(\mathbb{F}_{e})$ be a Chern character of positive rank, and assume
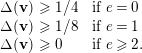 $$\begin{eqnarray}\begin{array}{@{}rcll@{}}\unicode[STIX]{x1D6E5}(\mathbf{v})\ & {\geqslant}\ & 1/4 & \text{if }e=0\\ \unicode[STIX]{x1D6E5}(\mathbf{v})\ & {\geqslant}\ & 1/8 & \text{if }e=1\\ \unicode[STIX]{x1D6E5}(\mathbf{v})\ & {\geqslant}\ & 0 & \text{if }e\geqslant 2.\\ ~\end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}rcll@{}}\unicode[STIX]{x1D6E5}(\mathbf{v})\ & {\geqslant}\ & 1/4 & \text{if }e=0\\ \unicode[STIX]{x1D6E5}(\mathbf{v})\ & {\geqslant}\ & 1/8 & \text{if }e=1\\ \unicode[STIX]{x1D6E5}(\mathbf{v})\ & {\geqslant}\ & 0 & \text{if }e\geqslant 2.\\ ~\end{array}\end{eqnarray}$$ Then there exists a line bundle  $L$ such that the inequalities (
$L$ such that the inequalities ( $\dagger$) hold.
$\dagger$) hold.
Proof. For simplicity we first assume  $\unicode[STIX]{x1D6E5}(\mathbf{v})>0$, and handle the case
$\unicode[STIX]{x1D6E5}(\mathbf{v})>0$, and handle the case  $\unicode[STIX]{x1D6E5}(\mathbf{v})=0$ (if
$\unicode[STIX]{x1D6E5}(\mathbf{v})=0$ (if  $e\geqslant 2$) later. Consider the curve
$e\geqslant 2$) later. Consider the curve  $Q:\unicode[STIX]{x1D712}(\mathbf{v}(-L_{a,b}))=0$ in the
$Q:\unicode[STIX]{x1D712}(\mathbf{v}(-L_{a,b}))=0$ in the  $(a,b)$-plane, where
$(a,b)$-plane, where  $L_{a,b}$ is the variable line bundle
$L_{a,b}$ is the variable line bundle
 $$\begin{eqnarray}L_{a,b}=\unicode[STIX]{x1D708}(\mathbf{v})-{\textstyle \frac{1}{2}}K_{X}+aE+bF\quad (a,b\in \mathbb{R})\end{eqnarray}$$
$$\begin{eqnarray}L_{a,b}=\unicode[STIX]{x1D708}(\mathbf{v})-{\textstyle \frac{1}{2}}K_{X}+aE+bF\quad (a,b\in \mathbb{R})\end{eqnarray}$$ “centered” at  $\unicode[STIX]{x1D708}(\mathbf{v})-{\textstyle \frac{1}{2}}K_{X}$. Then by Riemann–Roch,
$\unicode[STIX]{x1D708}(\mathbf{v})-{\textstyle \frac{1}{2}}K_{X}$. Then by Riemann–Roch,
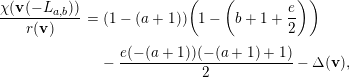 $$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x1D712}(\mathbf{v}(-L_{a,b}))}{r(\mathbf{v})} & = & \displaystyle (1-(a+1))\biggl(1-\biggl(b+1+\frac{e}{2}\biggr)\biggr)\nonumber\\ \displaystyle & & \displaystyle -\,\frac{e(-(a+1))(-(a+1)+1)}{2}-\unicode[STIX]{x1D6E5}(\mathbf{v}),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \frac{\unicode[STIX]{x1D712}(\mathbf{v}(-L_{a,b}))}{r(\mathbf{v})} & = & \displaystyle (1-(a+1))\biggl(1-\biggl(b+1+\frac{e}{2}\biggr)\biggr)\nonumber\\ \displaystyle & & \displaystyle -\,\frac{e(-(a+1))(-(a+1)+1)}{2}-\unicode[STIX]{x1D6E5}(\mathbf{v}),\nonumber\end{eqnarray}$$ so  $Q$ is the hyperbola
$Q$ is the hyperbola
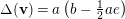 $$\begin{eqnarray}\unicode[STIX]{x1D6E5}(\mathbf{v})=a\left(b-{\textstyle \frac{1}{2}}ae\right)\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E5}(\mathbf{v})=a\left(b-{\textstyle \frac{1}{2}}ae\right)\end{eqnarray}$$with asymptotes
 $$\begin{eqnarray}\ell _{1}:a=0\quad \text{and}\quad \ell _{2}:b={\textstyle \frac{1}{2}}ae\end{eqnarray}$$
$$\begin{eqnarray}\ell _{1}:a=0\quad \text{and}\quad \ell _{2}:b={\textstyle \frac{1}{2}}ae\end{eqnarray}$$ meeting at the origin. Since  $\unicode[STIX]{x1D6E5}(\mathbf{v})>0$, the right branch
$\unicode[STIX]{x1D6E5}(\mathbf{v})>0$, the right branch  $Q_{1}$ (resp. left branch
$Q_{1}$ (resp. left branch  $Q_{2}$) of
$Q_{2}$) of  $Q$ lies right of
$Q$ lies right of  $\ell _{1}$ and above
$\ell _{1}$ and above  $\ell _{2}$ (resp. left of
$\ell _{2}$ (resp. left of  $\ell _{1}$ and below
$\ell _{1}$ and below  $\ell _{2}$). The function
$\ell _{2}$). The function  $\unicode[STIX]{x1D712}(\mathbf{v}(-L_{a,b}))$ is negative for any
$\unicode[STIX]{x1D712}(\mathbf{v}(-L_{a,b}))$ is negative for any  $(a,b)$ on
$(a,b)$ on  $\ell _{1}$, so it is negative for all points lying between the two branches and positive for all points which are either below
$\ell _{1}$, so it is negative for all points lying between the two branches and positive for all points which are either below  $Q_{2}$ or above
$Q_{2}$ or above  $Q_{1}$.
$Q_{1}$.
Those  $(a,b)\in \mathbb{R}^{2}$ such that
$(a,b)\in \mathbb{R}^{2}$ such that  $L_{a,b}$ is integral form a shift
$L_{a,b}$ is integral form a shift  $\unicode[STIX]{x1D6EC}\subset \mathbb{R}^{2}$ of the standard integral lattice
$\unicode[STIX]{x1D6EC}\subset \mathbb{R}^{2}$ of the standard integral lattice  $\mathbb{Z}^{2}\subset \mathbb{R}^{2}$. Thus to construct the line bundle
$\mathbb{Z}^{2}\subset \mathbb{R}^{2}$. Thus to construct the line bundle  $L$ we only need to find a point
$L$ we only need to find a point  $(a,b)\in \unicode[STIX]{x1D6EC}$ such that
$(a,b)\in \unicode[STIX]{x1D6EC}$ such that  $(a,b)$ lies below
$(a,b)$ lies below  $Q_{2}$ and the points
$Q_{2}$ and the points  $(a+1,b)$,
$(a+1,b)$,  $(a,b+1)$,
$(a,b+1)$,  $(a+1,b+1)$ lie between
$(a+1,b+1)$ lie between  $Q_{2}$ and
$Q_{2}$ and  $Q_{1}$. It is easy to find a point
$Q_{1}$. It is easy to find a point  $(a,b)\in \unicode[STIX]{x1D6EC}$ such that
$(a,b)\in \unicode[STIX]{x1D6EC}$ such that  $(a,b)$ lies below
$(a,b)$ lies below  $Q_{2}$ and
$Q_{2}$ and  $(a+1,b)$ and
$(a+1,b)$ and  $(a,b+1)$ are both above
$(a,b+1)$ are both above  $Q_{2}$: start from an arbitrary point
$Q_{2}$: start from an arbitrary point  $(a,b)\in \unicode[STIX]{x1D6EC}$ below
$(a,b)\in \unicode[STIX]{x1D6EC}$ below  $Q_{2}$ and repeatedly increment
$Q_{2}$ and repeatedly increment  $a$ and/or
$a$ and/or  $b$ by
$b$ by  $1$ until increasing either will cross
$1$ until increasing either will cross  $Q_{2}$. Let
$Q_{2}$. Let  $(a,b)\in \unicode[STIX]{x1D6EC}$ be any point below
$(a,b)\in \unicode[STIX]{x1D6EC}$ be any point below  $Q_{2}$ such that
$Q_{2}$ such that  $(a+1,b)$ and
$(a+1,b)$ and  $(a,b+1)$ are both above
$(a,b+1)$ are both above  $Q_{2}$. The point
$Q_{2}$. The point  $(a+1,b)$ still lies below
$(a+1,b)$ still lies below  $\ell _{2}$, and the point
$\ell _{2}$, and the point  $(a,b+1)$ still lies left of
$(a,b+1)$ still lies left of  $\ell _{1}$, from which we conclude that the points
$\ell _{1}$, from which we conclude that the points  $(a+1,b)$ and
$(a+1,b)$ and  $(a,b+1)$ both lie between
$(a,b+1)$ both lie between  $Q_{2}$ and
$Q_{2}$ and  $Q_{1}$. For this choice of
$Q_{1}$. For this choice of  $(a,b)$ we claim that additionally
$(a,b)$ we claim that additionally  $(a+1,b+1)$ is between
$(a+1,b+1)$ is between  $Q_{2}$ and
$Q_{2}$ and  $Q_{1}$.
$Q_{1}$.
Since  $Q_{2}$ can be described as the graph of a function
$Q_{2}$ can be described as the graph of a function  $b=f(a)$, the fact that
$b=f(a)$, the fact that  $(a+1,b)$ is above
$(a+1,b)$ is above  $Q_{2}$ implies
$Q_{2}$ implies  $(a+1,b+1)$ is above
$(a+1,b+1)$ is above  $Q_{2}$. It remains to show that
$Q_{2}$. It remains to show that  $(a+1,b+1)$ is below
$(a+1,b+1)$ is below  $Q_{1}$. If
$Q_{1}$. If  $e\geqslant 2$, then since
$e\geqslant 2$, then since  $(a,b)$ is below
$(a,b)$ is below  $\ell _{2}$ and
$\ell _{2}$ and  $\ell _{2}$ has slope
$\ell _{2}$ has slope  $e/2\geqslant 1$, we find that
$e/2\geqslant 1$, we find that  $(a+1,b+1)$ is below
$(a+1,b+1)$ is below  $\ell _{2}$ and hence
$\ell _{2}$ and hence  $(a+1,b+1)$ is below
$(a+1,b+1)$ is below  $Q_{1}$.
$Q_{1}$.
On the other hand, for  $e=0$ a simple computation shows that the translate of
$e=0$ a simple computation shows that the translate of  $Q_{2}$ by the vector
$Q_{2}$ by the vector  $(1,1)$ is disjoint from
$(1,1)$ is disjoint from  $Q_{1}$ if
$Q_{1}$ if  $\unicode[STIX]{x1D6E5}(\mathbf{v})>1/4$ and tangent to
$\unicode[STIX]{x1D6E5}(\mathbf{v})>1/4$ and tangent to  $Q_{1}$ if
$Q_{1}$ if  $\unicode[STIX]{x1D6E5}(\mathbf{v})=1/4$. Thus assuming
$\unicode[STIX]{x1D6E5}(\mathbf{v})=1/4$. Thus assuming  $\unicode[STIX]{x1D6E5}(\mathbf{v})\geqslant 1/4$, the point
$\unicode[STIX]{x1D6E5}(\mathbf{v})\geqslant 1/4$, the point  $(a+1,b+1)$ is on or below
$(a+1,b+1)$ is on or below  $Q_{1}$. An identical computation shows that an analogous result holds when
$Q_{1}$. An identical computation shows that an analogous result holds when  $e=1$ and
$e=1$ and  $\unicode[STIX]{x1D6E5}(\mathbf{v})\geqslant 1/8$.
$\unicode[STIX]{x1D6E5}(\mathbf{v})\geqslant 1/8$.
If  $e\geqslant 2$ and
$e\geqslant 2$ and  $\unicode[STIX]{x1D6E5}(\mathbf{v})=0$, the hyperbola
$\unicode[STIX]{x1D6E5}(\mathbf{v})=0$, the hyperbola  $Q$ degenerates to the union of lines
$Q$ degenerates to the union of lines  $\ell _{1}\cup \ell _{2}$, and a similar argument works. Thus a suitable line bundle
$\ell _{1}\cup \ell _{2}$, and a similar argument works. Thus a suitable line bundle  $L$ can be found in each case.◻
$L$ can be found in each case.◻
Remark 4.6. The stronger inequalities on  $\unicode[STIX]{x1D6E5}(\mathbf{v})$ needed in case
$\unicode[STIX]{x1D6E5}(\mathbf{v})$ needed in case  $e=0$ or
$e=0$ or  $e=1$ are in general necessary. For an easy example, suppose
$e=1$ are in general necessary. For an easy example, suppose  $e=0$,
$e=0$,  $\unicode[STIX]{x1D708}(\mathbf{v})={\textstyle \frac{1}{2}}E+{\textstyle \frac{1}{2}}F$ (so
$\unicode[STIX]{x1D708}(\mathbf{v})={\textstyle \frac{1}{2}}E+{\textstyle \frac{1}{2}}F$ (so  $r(\mathbf{v})$ is even), and assume
$r(\mathbf{v})$ is even), and assume  $0<\unicode[STIX]{x1D6E5}(\mathbf{v})<1/4$, which can certainly be arranged if
$0<\unicode[STIX]{x1D6E5}(\mathbf{v})<1/4$, which can certainly be arranged if  $r(\mathbf{v})$ is sufficiently large. The shifted lattice
$r(\mathbf{v})$ is sufficiently large. The shifted lattice  $\unicode[STIX]{x1D6EC}\subset \mathbb{R}^{2}$ is
$\unicode[STIX]{x1D6EC}\subset \mathbb{R}^{2}$ is  $\mathbb{Z}^{2}+({\textstyle \frac{1}{2}},{\textstyle \frac{1}{2}})$. The hyperbola
$\mathbb{Z}^{2}+({\textstyle \frac{1}{2}},{\textstyle \frac{1}{2}})$. The hyperbola  $Q$ becomes
$Q$ becomes  $ab=\unicode[STIX]{x1D6E5}(\mathbf{v})$, so the points
$ab=\unicode[STIX]{x1D6E5}(\mathbf{v})$, so the points  $(a,b)\in \unicode[STIX]{x1D6EC}$ such that
$(a,b)\in \unicode[STIX]{x1D6EC}$ such that  $\unicode[STIX]{x1D712}({\mathcal{V}}(-L_{a,b}))>0$ are exactly the points of
$\unicode[STIX]{x1D712}({\mathcal{V}}(-L_{a,b}))>0$ are exactly the points of  $\unicode[STIX]{x1D6EC}$ in the first and third quadrants. No choice
$\unicode[STIX]{x1D6EC}$ in the first and third quadrants. No choice  $(a,b)$ making the inequalities (
$(a,b)$ making the inequalities ( $\dagger$) hold exists, so no sheaf of character
$\dagger$) hold exists, so no sheaf of character  $\mathbf{v}$ admits a Gaeta-type resolution.
$\mathbf{v}$ admits a Gaeta-type resolution.
5 Globally generated bundles
Throughout this section we let  $\mathbf{v}\in K(\mathbb{F}_{e})$ be a character of positive rank such that
$\mathbf{v}\in K(\mathbb{F}_{e})$ be a character of positive rank such that  $\unicode[STIX]{x1D6E5}(\mathbf{v})\geqslant 0$ and
$\unicode[STIX]{x1D6E5}(\mathbf{v})\geqslant 0$ and  $\unicode[STIX]{x1D708}(\mathbf{v})$ is nef. In this section we classify those characters
$\unicode[STIX]{x1D708}(\mathbf{v})$ is nef. In this section we classify those characters  $\mathbf{v}$ such that the general sheaf
$\mathbf{v}$ such that the general sheaf  ${\mathcal{V}}\in {\mathcal{P}}_{F}(\mathbf{v})$ is globally generated. We say that
${\mathcal{V}}\in {\mathcal{P}}_{F}(\mathbf{v})$ is globally generated. We say that  $\mathbf{v}$ is globally generated if a general sheaf
$\mathbf{v}$ is globally generated if a general sheaf  ${\mathcal{V}}\in {\mathcal{P}}_{F}(\mathbf{v})$ is. There is no loss of generality in assuming
${\mathcal{V}}\in {\mathcal{P}}_{F}(\mathbf{v})$ is. There is no loss of generality in assuming  $\unicode[STIX]{x1D708}(\mathbf{v})$ is nef. Indeed, if
$\unicode[STIX]{x1D708}(\mathbf{v})$ is nef. Indeed, if  $r(\mathbf{v})\geqslant 2$ then the general sheaf
$r(\mathbf{v})\geqslant 2$ then the general sheaf  ${\mathcal{V}}\in {\mathcal{P}}_{F}(\mathbf{v})$ is a vector bundle, and if it is globally generated then
${\mathcal{V}}\in {\mathcal{P}}_{F}(\mathbf{v})$ is a vector bundle, and if it is globally generated then  $c_{1}(\mathbf{v})$ is nef by Lemma 2.12. In the rank 1 case, if
$c_{1}(\mathbf{v})$ is nef by Lemma 2.12. In the rank 1 case, if  $L$ is a line bundle and
$L$ is a line bundle and  $Z\subset X$ is a general collection of
$Z\subset X$ is a general collection of  $n$ points, then
$n$ points, then  $L\otimes I_{Z}$ can only be globally generated if
$L\otimes I_{Z}$ can only be globally generated if  $L$ is, and therefore
$L$ is, and therefore  $L$ is again nef by Lemma 2.12.
$L$ is again nef by Lemma 2.12.
Since  $\unicode[STIX]{x1D708}(\mathbf{v})$ is nef, it follows from Theorem 3.1 that a general
$\unicode[STIX]{x1D708}(\mathbf{v})$ is nef, it follows from Theorem 3.1 that a general  ${\mathcal{V}}\in {\mathcal{P}}_{F}(\mathbf{v})$ is nonspecial. While the substack of
${\mathcal{V}}\in {\mathcal{P}}_{F}(\mathbf{v})$ is nonspecial. While the substack of  ${\mathcal{P}}_{F}(\mathbf{v})$ of globally generated sheaves is not necessarily open, the substack of
${\mathcal{P}}_{F}(\mathbf{v})$ of globally generated sheaves is not necessarily open, the substack of  ${\mathcal{P}}_{F}(\mathbf{v})$ of globally generated sheaves with no higher cohomology is open. Thus, a character
${\mathcal{P}}_{F}(\mathbf{v})$ of globally generated sheaves with no higher cohomology is open. Thus, a character  $\mathbf{v}$ is globally generated if and only if there exists a sheaf
$\mathbf{v}$ is globally generated if and only if there exists a sheaf  ${\mathcal{V}}\in {\mathcal{P}}_{F}(\mathbf{v})$ which is globally generated and has no higher cohomology. As usual, if
${\mathcal{V}}\in {\mathcal{P}}_{F}(\mathbf{v})$ which is globally generated and has no higher cohomology. As usual, if  $\mathbf{v}$ is globally generated and there are
$\mathbf{v}$ is globally generated and there are  $\unicode[STIX]{x1D707}_{H}$-semistable sheaves of character
$\unicode[STIX]{x1D707}_{H}$-semistable sheaves of character  $\mathbf{v}$, then the general
$\mathbf{v}$, then the general  ${\mathcal{V}}\in M_{H}^{\unicode[STIX]{x1D707}\text{-}\mathit{ss}}(\mathbf{v})$ is also globally generated.
${\mathcal{V}}\in M_{H}^{\unicode[STIX]{x1D707}\text{-}\mathit{ss}}(\mathbf{v})$ is also globally generated.
The classification of globally generated Chern characters on  $\mathbb{F}_{e}$ falls into three main cases. First, if
$\mathbb{F}_{e}$ falls into three main cases. First, if  $\unicode[STIX]{x1D708}(\mathbf{v})\cdot F=0$, then we see that
$\unicode[STIX]{x1D708}(\mathbf{v})\cdot F=0$, then we see that  $\mathbf{v}$ can only be globally generated if it is pulled back from
$\mathbf{v}$ can only be globally generated if it is pulled back from  $\mathbb{P}^{1}$. This imposes strong restrictions on
$\mathbb{P}^{1}$. This imposes strong restrictions on  $\mathbf{v}$. When
$\mathbf{v}$. When  $\unicode[STIX]{x1D708}(\mathbf{v})\cdot F>0$, it is convenient to discuss two separate cases depending on the sign of
$\unicode[STIX]{x1D708}(\mathbf{v})\cdot F>0$, it is convenient to discuss two separate cases depending on the sign of  $\unicode[STIX]{x1D712}(\mathbf{v}(-F))$. Note that since
$\unicode[STIX]{x1D712}(\mathbf{v}(-F))$. Note that since  $\unicode[STIX]{x1D708}(\mathbf{v})$ is nef, we have
$\unicode[STIX]{x1D708}(\mathbf{v})$ is nef, we have  $\unicode[STIX]{x1D708}(\mathbf{v}(-F))\cdot F>0$ and
$\unicode[STIX]{x1D708}(\mathbf{v}(-F))\cdot F>0$ and  $\unicode[STIX]{x1D708}(\mathbf{v}(-F))\cdot E\geqslant -1$. Thus by Theorem 3.1, the cohomology of
$\unicode[STIX]{x1D708}(\mathbf{v}(-F))\cdot E\geqslant -1$. Thus by Theorem 3.1, the cohomology of  ${\mathcal{V}}(-F)$ is determined by its Euler characteristic. When
${\mathcal{V}}(-F)$ is determined by its Euler characteristic. When  $\unicode[STIX]{x1D712}(\mathbf{v}(-F))\geqslant 0,$ a general sheaf
$\unicode[STIX]{x1D712}(\mathbf{v}(-F))\geqslant 0,$ a general sheaf  ${\mathcal{V}}$ of character
${\mathcal{V}}$ of character  $\mathbf{v}$ has
$\mathbf{v}$ has  $H^{1}(\mathbb{F}_{e},{\mathcal{V}}(-F))=0$ and it is easy to prove global generation by restricting to a fiber. On the other hand when
$H^{1}(\mathbb{F}_{e},{\mathcal{V}}(-F))=0$ and it is easy to prove global generation by restricting to a fiber. On the other hand when  $\unicode[STIX]{x1D712}(\mathbf{v}(-F))<0$, any sheaf
$\unicode[STIX]{x1D712}(\mathbf{v}(-F))<0$, any sheaf  ${\mathcal{V}}$ of character
${\mathcal{V}}$ of character  $\mathbf{v}$ has
$\mathbf{v}$ has  $H^{1}(\mathbb{F}_{e},{\mathcal{V}}(-F))\neq 0$ and the restriction to a fiber is not so useful. In this case we construct globally generated vector bundles by first constructing a suitable “Lazarsfeld–Mukai” type bundle
$H^{1}(\mathbb{F}_{e},{\mathcal{V}}(-F))\neq 0$ and the restriction to a fiber is not so useful. In this case we construct globally generated vector bundles by first constructing a suitable “Lazarsfeld–Mukai” type bundle
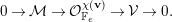 $$\begin{eqnarray}0\rightarrow {\mathcal{M}}\rightarrow {\mathcal{O}}_{\mathbb{F}_{e}}^{\unicode[STIX]{x1D712}(\mathbf{v})}\rightarrow {\mathcal{V}}\rightarrow 0.\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow {\mathcal{M}}\rightarrow {\mathcal{O}}_{\mathbb{F}_{e}}^{\unicode[STIX]{x1D712}(\mathbf{v})}\rightarrow {\mathcal{V}}\rightarrow 0.\end{eqnarray}$$ Our Gaeta-type resolutions provide a key tool in analyzing the bundle  ${\mathcal{M}}$.
${\mathcal{M}}$.
We now state the full classification theorems. The classification is slightly different depending on if  $e=0$,
$e=0$,  $e=1$, or
$e=1$, or  $e\geqslant 2$. To make the statements as clean as possible we state the
$e\geqslant 2$. To make the statements as clean as possible we state the  $e=0$ case separately.
$e=0$ case separately.
Theorem 5.1. Suppose  $e\geqslant 1$, and let
$e\geqslant 1$, and let  $\mathbf{v}\in K(\mathbb{F}_{e})$ be a Chern character of positive rank such that
$\mathbf{v}\in K(\mathbb{F}_{e})$ be a Chern character of positive rank such that  $\unicode[STIX]{x1D6E5}(\mathbf{v})\geqslant 0$ and
$\unicode[STIX]{x1D6E5}(\mathbf{v})\geqslant 0$ and  $\unicode[STIX]{x1D708}(\mathbf{v})$ is nef. Then
$\unicode[STIX]{x1D708}(\mathbf{v})$ is nef. Then  $\mathbf{v}$ is globally generated if and only if one of the following holds.
$\mathbf{v}$ is globally generated if and only if one of the following holds.
(1) We have
 $\unicode[STIX]{x1D708}(\mathbf{v})\cdot F=0$, and there are integers
$\unicode[STIX]{x1D708}(\mathbf{v})\cdot F=0$, and there are integers  $a,m\geqslant 0$ such that
$a,m\geqslant 0$ such that  $$\begin{eqnarray}\mathbf{v}=(r(\mathbf{v})-m)\operatorname{ch}{\mathcal{O}}_{\mathbb{F}_{e}}(aF)+m\operatorname{ch}{\mathcal{O}}_{\mathbb{F}_{e}}((a+1)F).\end{eqnarray}$$
$$\begin{eqnarray}\mathbf{v}=(r(\mathbf{v})-m)\operatorname{ch}{\mathcal{O}}_{\mathbb{F}_{e}}(aF)+m\operatorname{ch}{\mathcal{O}}_{\mathbb{F}_{e}}((a+1)F).\end{eqnarray}$$(2) We have
 $\unicode[STIX]{x1D708}(\mathbf{v})\cdot F>0$ and
$\unicode[STIX]{x1D708}(\mathbf{v})\cdot F>0$ and  $\unicode[STIX]{x1D712}(\mathbf{v}(-F))\geqslant 0$.
$\unicode[STIX]{x1D712}(\mathbf{v}(-F))\geqslant 0$.(3) We have
 $\unicode[STIX]{x1D708}(\mathbf{v})\cdot F>0$,
$\unicode[STIX]{x1D708}(\mathbf{v})\cdot F>0$,  $\unicode[STIX]{x1D712}(\mathbf{v}(-F))<0$, and
$\unicode[STIX]{x1D712}(\mathbf{v}(-F))<0$, and  $\unicode[STIX]{x1D712}(\mathbf{v})\geqslant r(\mathbf{v})+2$.
$\unicode[STIX]{x1D712}(\mathbf{v})\geqslant r(\mathbf{v})+2$.(4) We have
 $e=1$,
$e=1$,  $\unicode[STIX]{x1D708}(\mathbf{v})\cdot F>0$,
$\unicode[STIX]{x1D708}(\mathbf{v})\cdot F>0$,  $\unicode[STIX]{x1D712}(\mathbf{v}(-F))<0$,
$\unicode[STIX]{x1D712}(\mathbf{v}(-F))<0$,  $\unicode[STIX]{x1D712}(\mathbf{v})=r(\mathbf{v})+1$, and
$\unicode[STIX]{x1D712}(\mathbf{v})=r(\mathbf{v})+1$, and  $$\begin{eqnarray}\mathbf{v}=(r(\mathbf{v})+1)\operatorname{ch}{\mathcal{O}}_{\mathbb{F}_{1}}-\operatorname{ch}{\mathcal{O}}_{\mathbb{F}_{1}}(-2E-2F).\end{eqnarray}$$
$$\begin{eqnarray}\mathbf{v}=(r(\mathbf{v})+1)\operatorname{ch}{\mathcal{O}}_{\mathbb{F}_{1}}-\operatorname{ch}{\mathcal{O}}_{\mathbb{F}_{1}}(-2E-2F).\end{eqnarray}$$
The classification changes slightly in the case of  $\mathbb{P}^{1}\times \mathbb{P}^{1}$ since
$\mathbb{P}^{1}\times \mathbb{P}^{1}$ since  $F$ and
$F$ and  $E$ are the fiber classes for the two rulings.
$E$ are the fiber classes for the two rulings.
Theorem 5.2. Let  $\mathbf{v}\in K(\mathbb{P}^{1}\times \mathbb{P}^{1})$ be a Chern character of positive rank such that
$\mathbf{v}\in K(\mathbb{P}^{1}\times \mathbb{P}^{1})$ be a Chern character of positive rank such that  $\unicode[STIX]{x1D6E5}(\mathbf{v})\geqslant 0$ and
$\unicode[STIX]{x1D6E5}(\mathbf{v})\geqslant 0$ and  $\unicode[STIX]{x1D708}(\mathbf{v})$ is nef. Let
$\unicode[STIX]{x1D708}(\mathbf{v})$ is nef. Let  $F_{1},F_{2}$ be fibers in opposite rulings. Then
$F_{1},F_{2}$ be fibers in opposite rulings. Then  $\mathbf{v}$ is globally generated if and only if one of the following holds.
$\mathbf{v}$ is globally generated if and only if one of the following holds.
(1) We have
 $\unicode[STIX]{x1D708}(\mathbf{v})\cdot F_{i}=0$ for some
$\unicode[STIX]{x1D708}(\mathbf{v})\cdot F_{i}=0$ for some  $i\in \{1,2\}$, and there are integers
$i\in \{1,2\}$, and there are integers  $a,m\geqslant 0$ such that
$a,m\geqslant 0$ such that  $$\begin{eqnarray}\mathbf{v}=(r(\mathbf{v})-m)\operatorname{ch}{\mathcal{O}}_{\mathbb{P}^{1}\times \mathbb{P}^{1}}(aF_{i})+m\operatorname{ch}{\mathcal{O}}_{\mathbb{P}^{1}\times \mathbb{P}^{1}}((a+1)F_{i}).\end{eqnarray}$$
$$\begin{eqnarray}\mathbf{v}=(r(\mathbf{v})-m)\operatorname{ch}{\mathcal{O}}_{\mathbb{P}^{1}\times \mathbb{P}^{1}}(aF_{i})+m\operatorname{ch}{\mathcal{O}}_{\mathbb{P}^{1}\times \mathbb{P}^{1}}((a+1)F_{i}).\end{eqnarray}$$(2) We have
 $\unicode[STIX]{x1D708}(\mathbf{v})\cdot F_{i}>0$ for
$\unicode[STIX]{x1D708}(\mathbf{v})\cdot F_{i}>0$ for  $i=1,2$, but
$i=1,2$, but  $\unicode[STIX]{x1D712}(\mathbf{v}(-F_{j}))\geqslant 0$ for some
$\unicode[STIX]{x1D712}(\mathbf{v}(-F_{j}))\geqslant 0$ for some  $j\in \{1,2\}$.
$j\in \{1,2\}$.(3) We have
 $\unicode[STIX]{x1D708}(\mathbf{v})\cdot F_{i}>0$ and
$\unicode[STIX]{x1D708}(\mathbf{v})\cdot F_{i}>0$ and  $\unicode[STIX]{x1D712}(\mathbf{v}(-F_{i}))<0$ for
$\unicode[STIX]{x1D712}(\mathbf{v}(-F_{i}))<0$ for  $i=1,2$, and
$i=1,2$, and  $\unicode[STIX]{x1D712}(\mathbf{v})\geqslant r(\mathbf{v})+2$.
$\unicode[STIX]{x1D712}(\mathbf{v})\geqslant r(\mathbf{v})+2$.
We note that an analogous result for  $\mathbb{P}^{2}$ follows from the classification of globally generated characters on
$\mathbb{P}^{2}$ follows from the classification of globally generated characters on  $\mathbb{F}_{1}$. Let
$\mathbb{F}_{1}$. Let  $H\subset \mathbb{P}^{2}$ be the class of a line. We say a character
$H\subset \mathbb{P}^{2}$ be the class of a line. We say a character  $\mathbf{v}\in K(\mathbb{P}^{2})$ is globally generated if a general
$\mathbf{v}\in K(\mathbb{P}^{2})$ is globally generated if a general  $H$-prioritary sheaf is globally generated. By Hirschowitz–Laszlo [Reference Hirschowitz and LaszloHiL93] and Göttsche–Hirschowitz [Reference Göttsche and HirschowitzGHi94], the stack
$H$-prioritary sheaf is globally generated. By Hirschowitz–Laszlo [Reference Hirschowitz and LaszloHiL93] and Göttsche–Hirschowitz [Reference Göttsche and HirschowitzGHi94], the stack  ${\mathcal{P}}_{\mathbb{P}^{2},H}(\mathbf{v})$ is irreducible and a general
${\mathcal{P}}_{\mathbb{P}^{2},H}(\mathbf{v})$ is irreducible and a general  ${\mathcal{V}}\in {\mathcal{P}}_{\mathbb{P}^{2},H}(\mathbf{v})$ has only one nonzero cohomology group. This result completes the classification of globally generated characters on
${\mathcal{V}}\in {\mathcal{P}}_{\mathbb{P}^{2},H}(\mathbf{v})$ has only one nonzero cohomology group. This result completes the classification of globally generated characters on  $\mathbb{P}^{2}$ begun in Bertram et al. [Reference Bertram, Goller and JohnsonBGJ16].
$\mathbb{P}^{2}$ begun in Bertram et al. [Reference Bertram, Goller and JohnsonBGJ16].
Corollary 5.3. Let  $\mathbf{v}\in K(\mathbb{P}^{2})$ be a Chern character of positive rank such that
$\mathbf{v}\in K(\mathbb{P}^{2})$ be a Chern character of positive rank such that  $\unicode[STIX]{x1D6E5}(\mathbf{v})\geqslant 0$ and
$\unicode[STIX]{x1D6E5}(\mathbf{v})\geqslant 0$ and  $\unicode[STIX]{x1D707}(\mathbf{v})\geqslant 0$. Then
$\unicode[STIX]{x1D707}(\mathbf{v})\geqslant 0$. Then  $\mathbf{v}$ is globally generated if and only if one of the following holds.
$\mathbf{v}$ is globally generated if and only if one of the following holds.
(1) We have
 $\unicode[STIX]{x1D707}(\mathbf{v})=0$ and
$\unicode[STIX]{x1D707}(\mathbf{v})=0$ and  $\mathbf{v}=r(\mathbf{v})\operatorname{ch}{\mathcal{O}}_{\mathbb{P}^{2}}$.
$\mathbf{v}=r(\mathbf{v})\operatorname{ch}{\mathcal{O}}_{\mathbb{P}^{2}}$.(2) We have
 $\unicode[STIX]{x1D707}(\mathbf{v})>0$ and
$\unicode[STIX]{x1D707}(\mathbf{v})>0$ and  $\unicode[STIX]{x1D712}(\mathbf{v}(-1))\geqslant 0$.
$\unicode[STIX]{x1D712}(\mathbf{v}(-1))\geqslant 0$.(3) We have
 $\unicode[STIX]{x1D707}(\mathbf{v})>0$,
$\unicode[STIX]{x1D707}(\mathbf{v})>0$,  $\unicode[STIX]{x1D712}(\mathbf{v}(-1))<0$, and
$\unicode[STIX]{x1D712}(\mathbf{v}(-1))<0$, and  $\unicode[STIX]{x1D712}(\mathbf{v})\geqslant r(\mathbf{v})+2$.
$\unicode[STIX]{x1D712}(\mathbf{v})\geqslant r(\mathbf{v})+2$.(4) We have
 $\unicode[STIX]{x1D707}(\mathbf{v})>0$,
$\unicode[STIX]{x1D707}(\mathbf{v})>0$,  $\unicode[STIX]{x1D712}(\mathbf{v}(-1))<0$,
$\unicode[STIX]{x1D712}(\mathbf{v}(-1))<0$,  $\unicode[STIX]{x1D712}(\mathbf{v})=r(\mathbf{v})+1$, and
$\unicode[STIX]{x1D712}(\mathbf{v})=r(\mathbf{v})+1$, and  $$\begin{eqnarray}\mathbf{v}=(r(\mathbf{v})+1)\operatorname{ch}{\mathcal{O}}_{\mathbb{P}^{2}}-\operatorname{ch}{\mathcal{O}}_{\mathbb{P}^{2}}(-2).\end{eqnarray}$$
$$\begin{eqnarray}\mathbf{v}=(r(\mathbf{v})+1)\operatorname{ch}{\mathcal{O}}_{\mathbb{P}^{2}}-\operatorname{ch}{\mathcal{O}}_{\mathbb{P}^{2}}(-2).\end{eqnarray}$$
Proof. Let  $\unicode[STIX]{x1D70B}:\mathbb{F}_{1}\rightarrow \mathbb{P}^{2}$ be the blowdown map, and let
$\unicode[STIX]{x1D70B}:\mathbb{F}_{1}\rightarrow \mathbb{P}^{2}$ be the blowdown map, and let  $\mathbf{w}=\unicode[STIX]{x1D70B}^{\ast }(\mathbf{v})\in K(\mathbb{F}_{1})$ and
$\mathbf{w}=\unicode[STIX]{x1D70B}^{\ast }(\mathbf{v})\in K(\mathbb{F}_{1})$ and  $r=r(\mathbf{v})=r(\mathbf{w})$. The result is clear if
$r=r(\mathbf{v})=r(\mathbf{w})$. The result is clear if  $r=1$, since then the pullback of a general sheaf in
$r=1$, since then the pullback of a general sheaf in  ${\mathcal{P}}_{\mathbb{P}^{2},H}(\mathbf{v})$ is a general sheaf in
${\mathcal{P}}_{\mathbb{P}^{2},H}(\mathbf{v})$ is a general sheaf in  ${\mathcal{P}}_{\mathbb{F}_{1},F}(\mathbf{v})$, and clearly
${\mathcal{P}}_{\mathbb{F}_{1},F}(\mathbf{v})$, and clearly  $\mathbf{v}$ is globally generated if and only if
$\mathbf{v}$ is globally generated if and only if  $\mathbf{w}$ is. So suppose
$\mathbf{w}$ is. So suppose  $r\geqslant 2$.
$r\geqslant 2$.
The main technical difficulty is to compare the notions of  $F$-prioritary sheaves on
$F$-prioritary sheaves on  $\mathbb{F}_{1}$ and
$\mathbb{F}_{1}$ and  $H$-prioritary sheaves on
$H$-prioritary sheaves on  $\mathbb{P}^{2}$. We have
$\mathbb{P}^{2}$. We have  $c_{1}(\mathbf{w})\cdot E=0$ and
$c_{1}(\mathbf{w})\cdot E=0$ and  $\unicode[STIX]{x1D6E5}(\mathbf{w})=\unicode[STIX]{x1D6E5}(\mathbf{v})\geqslant 0$, so by Corollary 3.6 a general
$\unicode[STIX]{x1D6E5}(\mathbf{w})=\unicode[STIX]{x1D6E5}(\mathbf{v})\geqslant 0$, so by Corollary 3.6 a general  ${\mathcal{W}}\in {\mathcal{P}}_{\mathbb{F}_{1},F}(\mathbf{w})$ restricts to a trivial bundle on
${\mathcal{W}}\in {\mathcal{P}}_{\mathbb{F}_{1},F}(\mathbf{w})$ restricts to a trivial bundle on  $E$:
$E$:  ${\mathcal{W}}|_{E}\cong {\mathcal{O}}_{E}^{r}$. Furthermore, since
${\mathcal{W}}|_{E}\cong {\mathcal{O}}_{E}^{r}$. Furthermore, since  ${\mathcal{W}}$ is general it is actually
${\mathcal{W}}$ is general it is actually  $(E+F)$-prioritary. This can be shown by an argument similar to the proof of Lemma 3.3: since
$(E+F)$-prioritary. This can be shown by an argument similar to the proof of Lemma 3.3: since  $c_{1}(\mathbf{w})\cdot E=0$, we can construct a direct sum of line bundles
$c_{1}(\mathbf{w})\cdot E=0$, we can construct a direct sum of line bundles
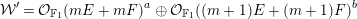 $$\begin{eqnarray}{\mathcal{W}}^{\prime }={\mathcal{O}}_{\mathbb{ F}_{1}}(mE+mF)^{a}\oplus {\mathcal{O}}_{\mathbb{F}_{1}}((m+1)E+(m+1)F)^{b}\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{W}}^{\prime }={\mathcal{O}}_{\mathbb{ F}_{1}}(mE+mF)^{a}\oplus {\mathcal{O}}_{\mathbb{F}_{1}}((m+1)E+(m+1)F)^{b}\end{eqnarray}$$ having the same rank and  $c_{1}$ as
$c_{1}$ as  $\mathbf{w}$. Then we compute
$\mathbf{w}$. Then we compute
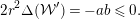 $$\begin{eqnarray}2r^{2}\unicode[STIX]{x1D6E5}({\mathcal{W}}^{\prime })=-ab\leqslant 0.\end{eqnarray}$$
$$\begin{eqnarray}2r^{2}\unicode[STIX]{x1D6E5}({\mathcal{W}}^{\prime })=-ab\leqslant 0.\end{eqnarray}$$ Since  $\unicode[STIX]{x1D6E5}(\mathbf{w})\geqslant 0$, we can obtain a sheaf of character
$\unicode[STIX]{x1D6E5}(\mathbf{w})\geqslant 0$, we can obtain a sheaf of character  $\mathbf{w}$ from
$\mathbf{w}$ from  ${\mathcal{W}}^{\prime }$ by repeated elementary modifications. Since
${\mathcal{W}}^{\prime }$ by repeated elementary modifications. Since  ${\mathcal{W}}^{\prime }$ is clearly
${\mathcal{W}}^{\prime }$ is clearly  $(E+F)$-prioritary, so is the general
$(E+F)$-prioritary, so is the general  ${\mathcal{W}}\in {\mathcal{P}}_{\mathbb{F}_{1},F}(\mathbf{w})$ by Lemma 2.7.
${\mathcal{W}}\in {\mathcal{P}}_{\mathbb{F}_{1},F}(\mathbf{w})$ by Lemma 2.7.
Furthermore,  $(E+F)$-prioritary vector bundles on
$(E+F)$-prioritary vector bundles on  $\mathbb{F}_{1}$ are automatically
$\mathbb{F}_{1}$ are automatically  $F$-prioritary. Indeed, if
$F$-prioritary. Indeed, if  ${\mathcal{W}}$ is an
${\mathcal{W}}$ is an  $(E+F)$-prioritary vector bundle, then the sequence
$(E+F)$-prioritary vector bundle, then the sequence
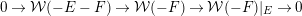 $$\begin{eqnarray}0\rightarrow {\mathcal{W}}(-E-F)\rightarrow {\mathcal{W}}(-F)\rightarrow {\mathcal{W}}(-F)|_{E}\rightarrow 0\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow {\mathcal{W}}(-E-F)\rightarrow {\mathcal{W}}(-F)\rightarrow {\mathcal{W}}(-F)|_{E}\rightarrow 0\end{eqnarray}$$yields
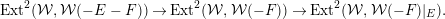 $$\begin{eqnarray}\operatorname{Ext}^{2}({\mathcal{W}},{\mathcal{W}}(-E-F))\rightarrow \operatorname{Ext}^{2}({\mathcal{W}},{\mathcal{W}}(-F))\rightarrow \operatorname{Ext}^{2}({\mathcal{W}},{\mathcal{W}}(-F)|_{E}).\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Ext}^{2}({\mathcal{W}},{\mathcal{W}}(-E-F))\rightarrow \operatorname{Ext}^{2}({\mathcal{W}},{\mathcal{W}}(-F))\rightarrow \operatorname{Ext}^{2}({\mathcal{W}},{\mathcal{W}}(-F)|_{E}).\end{eqnarray}$$ The first group vanishes by assumption, and the last vanishes since it is the  $H^{2}$ of a sheaf supported on a curve (as
$H^{2}$ of a sheaf supported on a curve (as  ${\mathcal{W}}$ is locally free). Therefore,
${\mathcal{W}}$ is locally free). Therefore,  ${\mathcal{W}}$ is
${\mathcal{W}}$ is  $F$-prioritary.
$F$-prioritary.
Now let  ${\mathcal{P}}^{\prime }\subset {\mathcal{P}}_{\mathbb{F}_{1},F}(\mathbf{w})$ be the open dense substack parameterizing
${\mathcal{P}}^{\prime }\subset {\mathcal{P}}_{\mathbb{F}_{1},F}(\mathbf{w})$ be the open dense substack parameterizing  $(E+F)$-prioritary vector bundles with restriction
$(E+F)$-prioritary vector bundles with restriction  ${\mathcal{W}}|_{E}\cong {\mathcal{O}}_{E}^{r}$, and let
${\mathcal{W}}|_{E}\cong {\mathcal{O}}_{E}^{r}$, and let  ${\mathcal{P}}^{\prime \prime }\subset {\mathcal{P}}_{\mathbb{P}^{2},H}(\mathbf{v})$ be the open dense substack parameterizing vector bundles. If
${\mathcal{P}}^{\prime \prime }\subset {\mathcal{P}}_{\mathbb{P}^{2},H}(\mathbf{v})$ be the open dense substack parameterizing vector bundles. If  ${\mathcal{W}}\in {\mathcal{P}}^{\prime }$, then
${\mathcal{W}}\in {\mathcal{P}}^{\prime }$, then  $\unicode[STIX]{x1D70B}_{\ast }{\mathcal{W}}$ is locally free and
$\unicode[STIX]{x1D70B}_{\ast }{\mathcal{W}}$ is locally free and  $\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D70B}_{\ast }{\mathcal{W}}\cong {\mathcal{W}}$ by Walter [Reference WalterWal98, Lemma 6]. Furthermore, we have an isomorphism
$\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D70B}_{\ast }{\mathcal{W}}\cong {\mathcal{W}}$ by Walter [Reference WalterWal98, Lemma 6]. Furthermore, we have an isomorphism  $\operatorname{Ext}^{2}({\mathcal{W}},{\mathcal{W}}(-E-F))\cong \operatorname{Ext}^{2}(\unicode[STIX]{x1D70B}_{\ast }{\mathcal{W}},\unicode[STIX]{x1D70B}_{\ast }{\mathcal{W}}(-H))$, which shows that
$\operatorname{Ext}^{2}({\mathcal{W}},{\mathcal{W}}(-E-F))\cong \operatorname{Ext}^{2}(\unicode[STIX]{x1D70B}_{\ast }{\mathcal{W}},\unicode[STIX]{x1D70B}_{\ast }{\mathcal{W}}(-H))$, which shows that  $\unicode[STIX]{x1D70B}_{\ast }{\mathcal{W}}$ is
$\unicode[STIX]{x1D70B}_{\ast }{\mathcal{W}}$ is  $H$-prioritary. Thus there is an induced map
$H$-prioritary. Thus there is an induced map  $\unicode[STIX]{x1D70B}_{\ast }:{\mathcal{P}}^{\prime }\rightarrow {\mathcal{P}}^{\prime \prime }$. On the other hand, if
$\unicode[STIX]{x1D70B}_{\ast }:{\mathcal{P}}^{\prime }\rightarrow {\mathcal{P}}^{\prime \prime }$. On the other hand, if  ${\mathcal{V}}\in {\mathcal{P}}^{\prime \prime }$ then
${\mathcal{V}}\in {\mathcal{P}}^{\prime \prime }$ then  $\unicode[STIX]{x1D70B}_{\ast }\unicode[STIX]{x1D70B}^{\ast }{\mathcal{V}}\cong {\mathcal{V}}$ since
$\unicode[STIX]{x1D70B}_{\ast }\unicode[STIX]{x1D70B}^{\ast }{\mathcal{V}}\cong {\mathcal{V}}$ since  ${\mathcal{V}}$ is a vector bundle and, furthermore,
${\mathcal{V}}$ is a vector bundle and, furthermore,  $\unicode[STIX]{x1D70B}^{\ast }{\mathcal{V}}$ is
$\unicode[STIX]{x1D70B}^{\ast }{\mathcal{V}}$ is  $(E+F)$-prioritary. Therefore,
$(E+F)$-prioritary. Therefore,  $\unicode[STIX]{x1D70B}^{\ast }{\mathcal{V}}\in {\mathcal{P}}^{\prime }$ and pullback gives an inverse map
$\unicode[STIX]{x1D70B}^{\ast }{\mathcal{V}}\in {\mathcal{P}}^{\prime }$ and pullback gives an inverse map  $\unicode[STIX]{x1D70B}^{\ast }:{\mathcal{P}}^{\prime \prime }\rightarrow {\mathcal{P}}^{\prime }$.
$\unicode[STIX]{x1D70B}^{\ast }:{\mathcal{P}}^{\prime \prime }\rightarrow {\mathcal{P}}^{\prime }$.
Under the correspondence between  ${\mathcal{P}}^{\prime }$ and
${\mathcal{P}}^{\prime }$ and  ${\mathcal{P}}^{\prime \prime }$, globally generated bundles correspond to globally generated bundles. We conclude that
${\mathcal{P}}^{\prime \prime }$, globally generated bundles correspond to globally generated bundles. We conclude that  $\mathbf{v}$ is globally generated if and only if
$\mathbf{v}$ is globally generated if and only if  $\mathbf{w}$ is globally generated, and the result follows from Theorem 5.1.◻
$\mathbf{w}$ is globally generated, and the result follows from Theorem 5.1.◻
Note that Corollary 5.3 can also be proved more directly by mimicking the proof of Theorem 5.1. We discuss each of the three main cases (1)–(3) of the classification in its own subsection.
5.1 Pullbacks
We begin the proof of the classification by analyzing the case  $\unicode[STIX]{x1D708}(\mathbf{v})\cdot F=0$. In this case a globally generated bundle must be a pullback from
$\unicode[STIX]{x1D708}(\mathbf{v})\cdot F=0$. In this case a globally generated bundle must be a pullback from  $\mathbb{P}^{1}$, which imposes strong restrictions on the character.
$\mathbb{P}^{1}$, which imposes strong restrictions on the character.
Proposition 5.4. Suppose  $\unicode[STIX]{x1D708}(\mathbf{v})\cdot F=0$. Then
$\unicode[STIX]{x1D708}(\mathbf{v})\cdot F=0$. Then  $\mathbf{v}$ is globally generated if and only if
$\mathbf{v}$ is globally generated if and only if  $\mathbf{v}$ is of the form
$\mathbf{v}$ is of the form
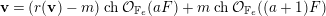 $$\begin{eqnarray}\mathbf{v}=(r(\mathbf{v})-m)\operatorname{ch}{\mathcal{O}}_{\mathbb{F}_{e}}(aF)+m\operatorname{ch}{\mathcal{O}}_{\mathbb{F}_{e}}((a+1)F)\end{eqnarray}$$
$$\begin{eqnarray}\mathbf{v}=(r(\mathbf{v})-m)\operatorname{ch}{\mathcal{O}}_{\mathbb{F}_{e}}(aF)+m\operatorname{ch}{\mathcal{O}}_{\mathbb{F}_{e}}((a+1)F)\end{eqnarray}$$ for some integers  $a,m\geqslant 0$.
$a,m\geqslant 0$.
Proof.  $(\Leftarrow )$ The bundles
$(\Leftarrow )$ The bundles
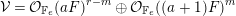 $$\begin{eqnarray}{\mathcal{V}}={\mathcal{O}}_{\mathbb{F}_{e}}(aF)^{r-m}\oplus {\mathcal{O}}_{\mathbb{F}_{e}}((a+1)F)^{m}\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{V}}={\mathcal{O}}_{\mathbb{F}_{e}}(aF)^{r-m}\oplus {\mathcal{O}}_{\mathbb{F}_{e}}((a+1)F)^{m}\end{eqnarray}$$ are  $F$-prioritary, globally generated, and have no higher cohomology, so their Chern characters are globally generated.
$F$-prioritary, globally generated, and have no higher cohomology, so their Chern characters are globally generated.
 $(\Rightarrow )$ Suppose
$(\Rightarrow )$ Suppose  ${\mathcal{V}}\in {\mathcal{P}}_{F}(\mathbf{v})$ is general and globally generated. The result is clear if
${\mathcal{V}}\in {\mathcal{P}}_{F}(\mathbf{v})$ is general and globally generated. The result is clear if  $r(\mathbf{v})=1$, so suppose
$r(\mathbf{v})=1$, so suppose  $r(\mathbf{v})\geqslant 2$. Then
$r(\mathbf{v})\geqslant 2$. Then  ${\mathcal{V}}$ is a vector bundle. The restriction
${\mathcal{V}}$ is a vector bundle. The restriction  ${\mathcal{V}}|_{F}$ to any fiber
${\mathcal{V}}|_{F}$ to any fiber  $F\cong \mathbb{P}^{1}$ of
$F\cong \mathbb{P}^{1}$ of  $\unicode[STIX]{x1D70B}:\mathbb{F}_{e}\rightarrow \mathbb{P}^{1}$ has degree
$\unicode[STIX]{x1D70B}:\mathbb{F}_{e}\rightarrow \mathbb{P}^{1}$ has degree  $0$. If any factor of
$0$. If any factor of  ${\mathcal{V}}|_{F}$ has negative degree, then
${\mathcal{V}}|_{F}$ has negative degree, then  ${\mathcal{V}}|_{F}$ is not globally generated, a contradiction. Therefore,
${\mathcal{V}}|_{F}$ is not globally generated, a contradiction. Therefore,  ${\mathcal{V}}|_{F}\cong {\mathcal{O}}_{F}^{r(\mathbf{v})}$ is trivial on each fiber. Consider the exact sequence
${\mathcal{V}}|_{F}\cong {\mathcal{O}}_{F}^{r(\mathbf{v})}$ is trivial on each fiber. Consider the exact sequence
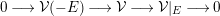 $$\begin{eqnarray}0\longrightarrow {\mathcal{V}}(-E)\longrightarrow {\mathcal{V}}\longrightarrow {\mathcal{V}}|_{E}\longrightarrow 0\end{eqnarray}$$
$$\begin{eqnarray}0\longrightarrow {\mathcal{V}}(-E)\longrightarrow {\mathcal{V}}\longrightarrow {\mathcal{V}}|_{E}\longrightarrow 0\end{eqnarray}$$ and apply  $\unicode[STIX]{x1D70B}_{\ast }$. Since
$\unicode[STIX]{x1D70B}_{\ast }$. Since  ${\mathcal{V}}(-E)|_{F}\cong {\mathcal{O}}_{F}(-1)^{r(\mathbf{v})}$ for any fiber
${\mathcal{V}}(-E)|_{F}\cong {\mathcal{O}}_{F}(-1)^{r(\mathbf{v})}$ for any fiber  $F$, we conclude that
$F$, we conclude that  $\unicode[STIX]{x1D70B}_{\ast }{\mathcal{V}}(-E)=R^{1}\unicode[STIX]{x1D70B}_{\ast }{\mathcal{V}}(-E)=0$ and
$\unicode[STIX]{x1D70B}_{\ast }{\mathcal{V}}(-E)=R^{1}\unicode[STIX]{x1D70B}_{\ast }{\mathcal{V}}(-E)=0$ and  $\unicode[STIX]{x1D70B}_{\ast }{\mathcal{V}}\cong \unicode[STIX]{x1D70B}_{\ast }({\mathcal{V}}|_{E})$. Hence, by [Reference WalterWal98, Lemma 5],
$\unicode[STIX]{x1D70B}_{\ast }{\mathcal{V}}\cong \unicode[STIX]{x1D70B}_{\ast }({\mathcal{V}}|_{E})$. Hence, by [Reference WalterWal98, Lemma 5],  ${\mathcal{V}}\cong \unicode[STIX]{x1D70B}^{\ast }(\unicode[STIX]{x1D70B}_{\ast }({\mathcal{V}}|_{E}))$. Since
${\mathcal{V}}\cong \unicode[STIX]{x1D70B}^{\ast }(\unicode[STIX]{x1D70B}_{\ast }({\mathcal{V}}|_{E}))$. Since  ${\mathcal{V}}|_{E}$ is balanced by Corollary 3.6, it follows that
${\mathcal{V}}|_{E}$ is balanced by Corollary 3.6, it follows that
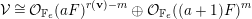 $$\begin{eqnarray}{\mathcal{V}}\cong {\mathcal{O}}_{\mathbb{F}_{e}}(aF)^{r(\mathbf{v})-m}\oplus {\mathcal{O}}_{\mathbb{F}_{e}}((a+1)F)^{m}\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{V}}\cong {\mathcal{O}}_{\mathbb{F}_{e}}(aF)^{r(\mathbf{v})-m}\oplus {\mathcal{O}}_{\mathbb{F}_{e}}((a+1)F)^{m}\end{eqnarray}$$ for some integers  $m\geqslant 0$ and
$m\geqslant 0$ and  $a\in \mathbb{Z}$. As
$a\in \mathbb{Z}$. As  ${\mathcal{V}}$ is globally generated,
${\mathcal{V}}$ is globally generated,  $a\geqslant 0$.◻
$a\geqslant 0$.◻
5.2 Restriction to a fiber
The case where  $\unicode[STIX]{x1D712}(\mathbf{v}(-F))\geqslant 0$ and
$\unicode[STIX]{x1D712}(\mathbf{v}(-F))\geqslant 0$ and  $\unicode[STIX]{x1D708}(\mathbf{v})\cdot F>0$ is the simplest to analyze.
$\unicode[STIX]{x1D708}(\mathbf{v})\cdot F>0$ is the simplest to analyze.
Proposition 5.5. Suppose  $\unicode[STIX]{x1D712}(\mathbf{v}(-F))\geqslant 0$ and
$\unicode[STIX]{x1D712}(\mathbf{v}(-F))\geqslant 0$ and  $\unicode[STIX]{x1D708}(\mathbf{v})\cdot F>0$. Then
$\unicode[STIX]{x1D708}(\mathbf{v})\cdot F>0$. Then  $\mathbf{v}$ is globally generated.
$\mathbf{v}$ is globally generated.
Proof. First suppose  $r(\mathbf{v})\geqslant 2$, so that the general
$r(\mathbf{v})\geqslant 2$, so that the general  ${\mathcal{V}}\in {\mathcal{P}}_{F}(\mathbf{v})$ is a vector bundle. Since
${\mathcal{V}}\in {\mathcal{P}}_{F}(\mathbf{v})$ is a vector bundle. Since  $\unicode[STIX]{x1D708}(\mathbf{v})\cdot F>0$, the bundle
$\unicode[STIX]{x1D708}(\mathbf{v})\cdot F>0$, the bundle  ${\mathcal{V}}$ restricts to a globally generated vector bundle on every fiber
${\mathcal{V}}$ restricts to a globally generated vector bundle on every fiber  $F$ of the projection
$F$ of the projection  $\unicode[STIX]{x1D70B}:\mathbb{F}_{e}\rightarrow \mathbb{P}^{1}$ by [Reference WalterWal98, Lemmas 3 and 4]. Let
$\unicode[STIX]{x1D70B}:\mathbb{F}_{e}\rightarrow \mathbb{P}^{1}$ by [Reference WalterWal98, Lemmas 3 and 4]. Let  ${\mathcal{V}}$ be such a bundle which also has no higher cohomology. Let
${\mathcal{V}}$ be such a bundle which also has no higher cohomology. Let  $p\in \mathbb{F}_{e}$ be any point, and let
$p\in \mathbb{F}_{e}$ be any point, and let  $F_{p}:=\unicode[STIX]{x1D70B}^{-1}(\unicode[STIX]{x1D70B}(p))$ be the fiber through
$F_{p}:=\unicode[STIX]{x1D70B}^{-1}(\unicode[STIX]{x1D70B}(p))$ be the fiber through  $p$. Since
$p$. Since  $\unicode[STIX]{x1D712}(\mathbf{v}(-F))\geqslant 0$, as explained in the introduction to this section, we know that
$\unicode[STIX]{x1D712}(\mathbf{v}(-F))\geqslant 0$, as explained in the introduction to this section, we know that  $H^{1}(\mathbb{F}_{e},{\mathcal{V}}(-F))=0$. Then the restriction sequence
$H^{1}(\mathbb{F}_{e},{\mathcal{V}}(-F))=0$. Then the restriction sequence
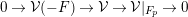 $$\begin{eqnarray}0\rightarrow {\mathcal{V}}(-F)\rightarrow {\mathcal{V}}\rightarrow {\mathcal{V}}|_{F_{p}}\rightarrow 0\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow {\mathcal{V}}(-F)\rightarrow {\mathcal{V}}\rightarrow {\mathcal{V}}|_{F_{p}}\rightarrow 0\end{eqnarray}$$ shows that  $H^{0}(\mathbb{F}_{e},{\mathcal{V}})\rightarrow H^{0}(F_{p},{\mathcal{V}}|_{F_{p}})$ is surjective. Since
$H^{0}(\mathbb{F}_{e},{\mathcal{V}})\rightarrow H^{0}(F_{p},{\mathcal{V}}|_{F_{p}})$ is surjective. Since  ${\mathcal{V}}|_{F_{p}}$ is globally generated, this implies that
${\mathcal{V}}|_{F_{p}}$ is globally generated, this implies that  ${\mathcal{V}}$ is globally generated at every point of
${\mathcal{V}}$ is globally generated at every point of  $F_{p}$. Therefore,
$F_{p}$. Therefore,  ${\mathcal{V}}$ is globally generated, and so is
${\mathcal{V}}$ is globally generated, and so is  $\mathbf{v}$.
$\mathbf{v}$.
If  $r(\mathbf{v})=1$, suppose the general sheaf of character
$r(\mathbf{v})=1$, suppose the general sheaf of character  $\mathbf{v}$ is of the form
$\mathbf{v}$ is of the form  $L\otimes I_{Z}$, where
$L\otimes I_{Z}$, where  $L$ is a nef line bundle and
$L$ is a nef line bundle and  $Z\subset X$ is a collection of
$Z\subset X$ is a collection of  $n$ general points. For
$n$ general points. For  $p\in \mathbb{F}_{e}$ we have an exact sequence of one of the following two forms, depending on whether or not the fiber
$p\in \mathbb{F}_{e}$ we have an exact sequence of one of the following two forms, depending on whether or not the fiber  $F_{p}$ contains a point of
$F_{p}$ contains a point of  $Z$:
$Z$:
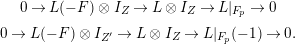 $$\begin{eqnarray}\displaystyle & \displaystyle 0\rightarrow L(-F)\otimes I_{Z}\rightarrow L\otimes I_{Z}\rightarrow L|_{F_{p}}\rightarrow 0 & \displaystyle \nonumber\\ \displaystyle & \displaystyle 0\rightarrow L(-F)\otimes I_{Z^{\prime }}\rightarrow L\otimes I_{Z}\rightarrow L|_{F_{p}}(-1)\rightarrow 0. & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle 0\rightarrow L(-F)\otimes I_{Z}\rightarrow L\otimes I_{Z}\rightarrow L|_{F_{p}}\rightarrow 0 & \displaystyle \nonumber\\ \displaystyle & \displaystyle 0\rightarrow L(-F)\otimes I_{Z^{\prime }}\rightarrow L\otimes I_{Z}\rightarrow L|_{F_{p}}(-1)\rightarrow 0. & \displaystyle \nonumber\end{eqnarray}$$ Here  $Z^{\prime }\subset Z$ consists of
$Z^{\prime }\subset Z$ consists of  $n-1$ points, with the
$n-1$ points, with the  $n$th point of
$n$th point of  $Z$ lying on
$Z$ lying on  $F_{p}$. Note that both
$F_{p}$. Note that both  $L(-F)\otimes I_{Z}$ and
$L(-F)\otimes I_{Z}$ and  $L(-F)\otimes I_{Z^{\prime }}$ have no higher cohomology, and
$L(-F)\otimes I_{Z^{\prime }}$ have no higher cohomology, and  $L|_{F_{p}}$ and
$L|_{F_{p}}$ and  $L|_{F_{p}}(-1)$ are both globally generated. Therefore,
$L|_{F_{p}}(-1)$ are both globally generated. Therefore,  $L\otimes I_{Z}$ is globally generated except possibly at points in
$L\otimes I_{Z}$ is globally generated except possibly at points in  $Z$. So suppose
$Z$. So suppose  $p\in Z$. In this case, we can construct two curves in
$p\in Z$. In this case, we can construct two curves in  $\mathbb{F}_{e}$:
$\mathbb{F}_{e}$:
(1) There is a curve
 $C$ of class
$C$ of class  $L$ that contains
$L$ that contains  $Z$ and intersects
$Z$ and intersects  $F_{p}$ transversely.
$F_{p}$ transversely.(2) Since
 $\unicode[STIX]{x1D712}(L(-F)\otimes I_{Z^{\prime }})>0$, there is a curve
$\unicode[STIX]{x1D712}(L(-F)\otimes I_{Z^{\prime }})>0$, there is a curve  $D$ of class
$D$ of class  $L(-F)$ which contains
$L(-F)$ which contains  $Z^{\prime }$ and does not contain
$Z^{\prime }$ and does not contain  $p$. (Note that the points in
$p$. (Note that the points in  $Z$ are general, so impose the expected number of conditions on sections of
$Z$ are general, so impose the expected number of conditions on sections of  $L(-F)$.)
$L(-F)$.)
Then the curves  $C$ and
$C$ and  $D+F$ give two sections of
$D+F$ give two sections of  $L$ which contain
$L$ which contain  $Z$ and intersect transversely at
$Z$ and intersect transversely at  $p$. Therefore,
$p$. Therefore,  $L\otimes I_{Z}$ is globally generated at
$L\otimes I_{Z}$ is globally generated at  $p$.◻
$p$.◻
5.3 Lazarsfeld–Mukai bundles
It remains to classify globally generated characters  $\mathbf{v}$ with
$\mathbf{v}$ with  $\unicode[STIX]{x1D712}(\mathbf{v}(-F))<0$ and
$\unicode[STIX]{x1D712}(\mathbf{v}(-F))<0$ and  $\unicode[STIX]{x1D708}(\mathbf{v})\cdot F>0$. Throughout this section, we put
$\unicode[STIX]{x1D708}(\mathbf{v})\cdot F>0$. Throughout this section, we put
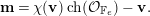 $$\begin{eqnarray}\mathbf{m}=\unicode[STIX]{x1D712}(\mathbf{v})\operatorname{ch}({\mathcal{O}}_{\mathbb{F}_{e}})-\mathbf{v}.\end{eqnarray}$$
$$\begin{eqnarray}\mathbf{m}=\unicode[STIX]{x1D712}(\mathbf{v})\operatorname{ch}({\mathcal{O}}_{\mathbb{F}_{e}})-\mathbf{v}.\end{eqnarray}$$ Thus, if  $\mathbf{v}$ is globally generated, then
$\mathbf{v}$ is globally generated, then  $\mathbf{m}$ is the character of the Lazarsfeld–Mukai bundle
$\mathbf{m}$ is the character of the Lazarsfeld–Mukai bundle
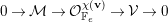 $$\begin{eqnarray}0\rightarrow {\mathcal{M}}\rightarrow {\mathcal{O}}_{\mathbb{F}_{e}}^{\unicode[STIX]{x1D712}(\mathbf{v})}\rightarrow {\mathcal{V}}\rightarrow 0\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow {\mathcal{M}}\rightarrow {\mathcal{O}}_{\mathbb{F}_{e}}^{\unicode[STIX]{x1D712}(\mathbf{v})}\rightarrow {\mathcal{V}}\rightarrow 0\end{eqnarray}$$which is the kernel of the canonical evaluation map. The next lemma is the main tool we use in this case.
Lemma 5.7. Suppose  $\unicode[STIX]{x1D712}(\mathbf{v}(-F))<0$. Then
$\unicode[STIX]{x1D712}(\mathbf{v}(-F))<0$. Then  $\mathbf{v}$ is globally generated if and only if there is a vector bundle
$\mathbf{v}$ is globally generated if and only if there is a vector bundle  ${\mathcal{M}}$ of character
${\mathcal{M}}$ of character  $\mathbf{m}$ such that
$\mathbf{m}$ such that
(1)
 ${\mathcal{M}}$ has no cohomology,
${\mathcal{M}}$ has no cohomology,(2)
 $h^{1}(\mathbb{F}_{e},{\mathcal{M}}(-F))=0$, and
$h^{1}(\mathbb{F}_{e},{\mathcal{M}}(-F))=0$, and(3)
 ${\mathcal{M}}^{\ast }$ is globally generated.
${\mathcal{M}}^{\ast }$ is globally generated.
Proof. ( $\Rightarrow$) Suppose
$\Rightarrow$) Suppose  $\mathbf{v}$ is globally generated. Then there is a globally generated (torsion-free) sheaf
$\mathbf{v}$ is globally generated. Then there is a globally generated (torsion-free) sheaf  ${\mathcal{V}}\in {\mathcal{P}}_{F}(\mathbf{v})$ which has no higher cohomology. Furthermore, since
${\mathcal{V}}\in {\mathcal{P}}_{F}(\mathbf{v})$ which has no higher cohomology. Furthermore, since  $\unicode[STIX]{x1D712}({\mathcal{V}}(-F))<0$ we can assume
$\unicode[STIX]{x1D712}({\mathcal{V}}(-F))<0$ we can assume  ${\mathcal{V}}(-F)$ only has
${\mathcal{V}}(-F)$ only has  $h^{1}$. Then the kernel
$h^{1}$. Then the kernel  ${\mathcal{M}}$ of the canonical evaluation map
${\mathcal{M}}$ of the canonical evaluation map
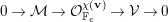 $$\begin{eqnarray}0\rightarrow {\mathcal{M}}\rightarrow {\mathcal{O}}_{\mathbb{F}_{e}}^{\unicode[STIX]{x1D712}(\mathbf{v})}\rightarrow {\mathcal{V}}\rightarrow 0\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow {\mathcal{M}}\rightarrow {\mathcal{O}}_{\mathbb{F}_{e}}^{\unicode[STIX]{x1D712}(\mathbf{v})}\rightarrow {\mathcal{V}}\rightarrow 0\end{eqnarray}$$has the required properties.
( $\Leftarrow$) Conversely, suppose there is a vector bundle
$\Leftarrow$) Conversely, suppose there is a vector bundle  ${\mathcal{M}}$ of character
${\mathcal{M}}$ of character  $\mathbf{m}$ with properties (1)–(3). Let
$\mathbf{m}$ with properties (1)–(3). Let  ${\mathcal{V}}$ be a sheaf defined as the cokernel of a general map
${\mathcal{V}}$ be a sheaf defined as the cokernel of a general map  $\unicode[STIX]{x1D719}:{\mathcal{M}}\rightarrow {\mathcal{O}}_{\mathbb{F}_{e}}^{\unicode[STIX]{x1D712}(\mathbf{v})}$. Since
$\unicode[STIX]{x1D719}:{\mathcal{M}}\rightarrow {\mathcal{O}}_{\mathbb{F}_{e}}^{\unicode[STIX]{x1D712}(\mathbf{v})}$. Since  $r(\mathbf{v})\geqslant 1$ and
$r(\mathbf{v})\geqslant 1$ and  ${\mathcal{M}}^{\ast }$ is globally generated, the map
${\mathcal{M}}^{\ast }$ is globally generated, the map  $\unicode[STIX]{x1D719}$ is injective and
$\unicode[STIX]{x1D719}$ is injective and  ${\mathcal{V}}$ is torsion-free (see [Reference HuizengaHui16, Proposition 2.6], and the proof of Theorem 2.10). The sequence
${\mathcal{V}}$ is torsion-free (see [Reference HuizengaHui16, Proposition 2.6], and the proof of Theorem 2.10). The sequence
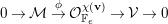 $$\begin{eqnarray}0\rightarrow {\mathcal{M}}\stackrel{\unicode[STIX]{x1D719}}{\rightarrow }{\mathcal{O}}_{\mathbb{F}_{e}}^{\unicode[STIX]{x1D712}(\mathbf{v})}\rightarrow {\mathcal{V}}\rightarrow 0\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow {\mathcal{M}}\stackrel{\unicode[STIX]{x1D719}}{\rightarrow }{\mathcal{O}}_{\mathbb{F}_{e}}^{\unicode[STIX]{x1D712}(\mathbf{v})}\rightarrow {\mathcal{V}}\rightarrow 0\end{eqnarray}$$ shows that  ${\mathcal{V}}$ is globally generated, and
${\mathcal{V}}$ is globally generated, and  ${\mathcal{V}}$ has no higher cohomology since
${\mathcal{V}}$ has no higher cohomology since  ${\mathcal{M}}$ and
${\mathcal{M}}$ and  ${\mathcal{O}}_{\mathbb{F}_{e}}$ have no higher cohomology.
${\mathcal{O}}_{\mathbb{F}_{e}}$ have no higher cohomology.
Finally, we must check that  ${\mathcal{V}}$ is
${\mathcal{V}}$ is  $F$-prioritary. But
$F$-prioritary. But  $\operatorname{Ext}^{2}({\mathcal{V}},{\mathcal{V}}(-F))$ is a quotient of a direct sum of copies of
$\operatorname{Ext}^{2}({\mathcal{V}},{\mathcal{V}}(-F))$ is a quotient of a direct sum of copies of
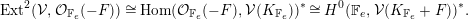 $$\begin{eqnarray}\operatorname{Ext}^{2}({\mathcal{V}},{\mathcal{O}}_{\mathbb{ F}_{e}}(-F))\cong \operatorname{Hom}({\mathcal{O}}_{\mathbb{F}_{e}}(-F),{\mathcal{V}}(K_{\mathbb{F}_{e}}))^{\ast }\cong H^{0}(\mathbb{F}_{e},{\mathcal{V}}(K_{\mathbb{F}_{e}}+F))^{\ast }.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Ext}^{2}({\mathcal{V}},{\mathcal{O}}_{\mathbb{ F}_{e}}(-F))\cong \operatorname{Hom}({\mathcal{O}}_{\mathbb{F}_{e}}(-F),{\mathcal{V}}(K_{\mathbb{F}_{e}}))^{\ast }\cong H^{0}(\mathbb{F}_{e},{\mathcal{V}}(K_{\mathbb{F}_{e}}+F))^{\ast }.\end{eqnarray}$$ There is an injection  ${\mathcal{V}}(K_{\mathbb{F}_{e}}+F)\rightarrow {\mathcal{V}}(-F)$ since
${\mathcal{V}}(K_{\mathbb{F}_{e}}+F)\rightarrow {\mathcal{V}}(-F)$ since  $-F-(K_{\mathbb{F}_{e}}+F)=2E+eF$ is effective, and
$-F-(K_{\mathbb{F}_{e}}+F)=2E+eF$ is effective, and  $H^{0}(\mathbb{F}_{e},{\mathcal{V}}(-F))=0$ since we are assuming
$H^{0}(\mathbb{F}_{e},{\mathcal{V}}(-F))=0$ since we are assuming  $H^{1}(\mathbb{F}_{e},{\mathcal{M}}(-F))=0$. Therefore,
$H^{1}(\mathbb{F}_{e},{\mathcal{M}}(-F))=0$. Therefore,  $H^{0}(\mathbb{F}_{e},{\mathcal{V}}(K_{\mathbb{F}_{e}}+F))=0$ and
$H^{0}(\mathbb{F}_{e},{\mathcal{V}}(K_{\mathbb{F}_{e}}+F))=0$ and  $\operatorname{Ext}^{2}({\mathcal{V}},{\mathcal{V}}(-F))=0$.◻
$\operatorname{Ext}^{2}({\mathcal{V}},{\mathcal{V}}(-F))=0$.◻
The remainder of the classification of globally generated characters  $\mathbf{v}$ with
$\mathbf{v}$ with  $\unicode[STIX]{x1D712}(\mathbf{v})\leqslant r(\mathbf{v})+1$ follows quickly; there is only one such character that was not already studied in the previous subsections.
$\unicode[STIX]{x1D712}(\mathbf{v})\leqslant r(\mathbf{v})+1$ follows quickly; there is only one such character that was not already studied in the previous subsections.
Corollary 5.8. Suppose  $\unicode[STIX]{x1D712}(\mathbf{v}(-F))<0$,
$\unicode[STIX]{x1D712}(\mathbf{v}(-F))<0$,  $\unicode[STIX]{x1D708}(\mathbf{v})\cdot F>0$, and
$\unicode[STIX]{x1D708}(\mathbf{v})\cdot F>0$, and  $\unicode[STIX]{x1D712}(\mathbf{v})\leqslant r(\mathbf{v})+1$. If
$\unicode[STIX]{x1D712}(\mathbf{v})\leqslant r(\mathbf{v})+1$. If  $e=0$, then further assume
$e=0$, then further assume  $\unicode[STIX]{x1D712}(\mathbf{v}(-E))<0$ and
$\unicode[STIX]{x1D712}(\mathbf{v}(-E))<0$ and  $\unicode[STIX]{x1D708}(\mathbf{v})\cdot E>0$. Then
$\unicode[STIX]{x1D708}(\mathbf{v})\cdot E>0$. Then  $\mathbf{v}$ is globally generated if and only if
$\mathbf{v}$ is globally generated if and only if  $e=1$ and
$e=1$ and
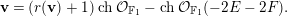 $$\begin{eqnarray}\mathbf{v}=(r(\mathbf{v})+1)\operatorname{ch}{\mathcal{O}}_{\mathbb{F}_{1}}-\operatorname{ch}{\mathcal{O}}_{\mathbb{F}_{1}}(-2E-2F).\end{eqnarray}$$
$$\begin{eqnarray}\mathbf{v}=(r(\mathbf{v})+1)\operatorname{ch}{\mathcal{O}}_{\mathbb{F}_{1}}-\operatorname{ch}{\mathcal{O}}_{\mathbb{F}_{1}}(-2E-2F).\end{eqnarray}$$Proof. ( $\Rightarrow$) Suppose
$\Rightarrow$) Suppose  $\mathbf{v}$ is globally generated, and let
$\mathbf{v}$ is globally generated, and let  ${\mathcal{V}}$ be a globally generated sheaf of character
${\mathcal{V}}$ be a globally generated sheaf of character  $\mathbf{v}$ with no higher cohomology. Then
$\mathbf{v}$ with no higher cohomology. Then  $\unicode[STIX]{x1D712}(\mathbf{v})=h^{0}(\mathbb{F}_{e},{\mathcal{V}})$, so
$\unicode[STIX]{x1D712}(\mathbf{v})=h^{0}(\mathbb{F}_{e},{\mathcal{V}})$, so  $\unicode[STIX]{x1D712}(\mathbf{v})\geqslant r(\mathbf{v})$. If
$\unicode[STIX]{x1D712}(\mathbf{v})\geqslant r(\mathbf{v})$. If  $\unicode[STIX]{x1D712}(\mathbf{v})=r(\mathbf{v})$ then we must have
$\unicode[STIX]{x1D712}(\mathbf{v})=r(\mathbf{v})$ then we must have  ${\mathcal{V}}\cong {\mathcal{O}}_{\mathbb{F}_{e}}^{r(\mathbf{v})}$, but then
${\mathcal{V}}\cong {\mathcal{O}}_{\mathbb{F}_{e}}^{r(\mathbf{v})}$, but then  $\unicode[STIX]{x1D708}(\mathbf{v})\cdot F=0$. So, going forward we may assume
$\unicode[STIX]{x1D708}(\mathbf{v})\cdot F=0$. So, going forward we may assume  $\unicode[STIX]{x1D712}(\mathbf{v})=r(\mathbf{v})+1$. By Lemma 5.7, the kernel
$\unicode[STIX]{x1D712}(\mathbf{v})=r(\mathbf{v})+1$. By Lemma 5.7, the kernel  ${\mathcal{M}}$ of a general evaluation map
${\mathcal{M}}$ of a general evaluation map
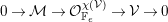 $$\begin{eqnarray}0\rightarrow {\mathcal{M}}\rightarrow {\mathcal{O}}_{\mathbb{F}_{e}}^{\unicode[STIX]{x1D712}({\mathcal{V}})}\rightarrow {\mathcal{V}}\rightarrow 0\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow {\mathcal{M}}\rightarrow {\mathcal{O}}_{\mathbb{F}_{e}}^{\unicode[STIX]{x1D712}({\mathcal{V}})}\rightarrow {\mathcal{V}}\rightarrow 0\end{eqnarray}$$ is a line bundle with no cohomology such that  $H^{1}(\mathbb{F}_{e},{\mathcal{M}}(-F))=0$ and
$H^{1}(\mathbb{F}_{e},{\mathcal{M}}(-F))=0$ and  ${\mathcal{M}}^{\ast }$ is globally generated. Suppose
${\mathcal{M}}^{\ast }$ is globally generated. Suppose  ${\mathcal{M}}={\mathcal{O}}_{\mathbb{F}_{e}}(-aE-bF)$. Since
${\mathcal{M}}={\mathcal{O}}_{\mathbb{F}_{e}}(-aE-bF)$. Since  ${\mathcal{M}}^{\ast }$ is globally generated, we have
${\mathcal{M}}^{\ast }$ is globally generated, we have  $a\geqslant 0$ and
$a\geqslant 0$ and  $b\geqslant ae$. Since
$b\geqslant ae$. Since  $\unicode[STIX]{x1D708}({\mathcal{V}})\cdot F>0$, we further have
$\unicode[STIX]{x1D708}({\mathcal{V}})\cdot F>0$, we further have  $a>0$. If
$a>0$. If  $a=1$, then
$a=1$, then  $\unicode[STIX]{x1D712}({\mathcal{M}}(-F))=\unicode[STIX]{x1D712}({\mathcal{O}}_{\mathbb{F}_{e}}(-F))=0$ and so
$\unicode[STIX]{x1D712}({\mathcal{M}}(-F))=\unicode[STIX]{x1D712}({\mathcal{O}}_{\mathbb{F}_{e}}(-F))=0$ and so  $\unicode[STIX]{x1D712}({\mathcal{V}}(-F))=0$, a contradiction. Therefore,
$\unicode[STIX]{x1D712}({\mathcal{V}}(-F))=0$, a contradiction. Therefore,  $a\geqslant 2$ and so
$a\geqslant 2$ and so  $b\geqslant 2e$. Then
$b\geqslant 2e$. Then
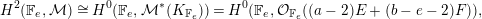 $$\begin{eqnarray}H^{2}(\mathbb{F}_{e},{\mathcal{M}})\cong H^{0}(\mathbb{F}_{e},{\mathcal{M}}^{\ast }(K_{\mathbb{ F}_{e}}))=H^{0}(\mathbb{F}_{e},{\mathcal{O}}_{\mathbb{F}_{e}}((a-2)E+(b-e-2)F)),\end{eqnarray}$$
$$\begin{eqnarray}H^{2}(\mathbb{F}_{e},{\mathcal{M}})\cong H^{0}(\mathbb{F}_{e},{\mathcal{M}}^{\ast }(K_{\mathbb{ F}_{e}}))=H^{0}(\mathbb{F}_{e},{\mathcal{O}}_{\mathbb{F}_{e}}((a-2)E+(b-e-2)F)),\end{eqnarray}$$ and since  ${\mathcal{M}}$ has no cohomology we must have
${\mathcal{M}}$ has no cohomology we must have  $b<e+2$. But
$b<e+2$. But  $b\geqslant 2e$ and
$b\geqslant 2e$ and  $b<e+2$ together imply
$b<e+2$ together imply  $e\in \{0,1\}$. If
$e\in \{0,1\}$. If  $e=0$, then since
$e=0$, then since  $a\geqslant 2$ we find by symmetry that we must also have
$a\geqslant 2$ we find by symmetry that we must also have  $b\geqslant 2$. But then
$b\geqslant 2$. But then  ${\mathcal{M}}$ has
${\mathcal{M}}$ has  $h^{2}$, so there is no suitable
$h^{2}$, so there is no suitable  ${\mathcal{M}}$. If
${\mathcal{M}}$. If  $e=1$, then the only possibility is
$e=1$, then the only possibility is  $a=b=2$.
$a=b=2$.
( $\Leftarrow$) Conversely, for any integer
$\Leftarrow$) Conversely, for any integer  $r\geqslant 1$ the cokernel
$r\geqslant 1$ the cokernel  ${\mathcal{V}}$ of a general injection
${\mathcal{V}}$ of a general injection
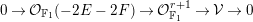 $$\begin{eqnarray}0\rightarrow {\mathcal{O}}_{\mathbb{F}_{1}}(-2E-2F)\rightarrow {\mathcal{O}}_{\mathbb{F}_{1}}^{r+1}\rightarrow {\mathcal{V}}\rightarrow 0\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow {\mathcal{O}}_{\mathbb{F}_{1}}(-2E-2F)\rightarrow {\mathcal{O}}_{\mathbb{F}_{1}}^{r+1}\rightarrow {\mathcal{V}}\rightarrow 0\end{eqnarray}$$ is a globally generated torsion-free sheaf with no higher cohomology, and  $\mathbf{v}$ satisfies the necessary hypotheses.◻
$\mathbf{v}$ satisfies the necessary hypotheses.◻
Finally, we construct bundles  ${\mathcal{M}}$ with the necessary properties in the remaining cases. We write
${\mathcal{M}}$ with the necessary properties in the remaining cases. We write  $\mathbf{m}^{D}$ for the Serre dual character
$\mathbf{m}^{D}$ for the Serre dual character  $\mathbf{m}^{\ast }(K_{X})$. The next lemma will allow us to apply our theory of Gaeta-type resolutions to study bundles of character
$\mathbf{m}^{\ast }(K_{X})$. The next lemma will allow us to apply our theory of Gaeta-type resolutions to study bundles of character  $\mathbf{m}$.
$\mathbf{m}$.
Lemma 5.9. Suppose  $\unicode[STIX]{x1D712}(\mathbf{v}(-F))<0$,
$\unicode[STIX]{x1D712}(\mathbf{v}(-F))<0$,  $\unicode[STIX]{x1D708}(\mathbf{v})\cdot F<0$, and
$\unicode[STIX]{x1D708}(\mathbf{v})\cdot F<0$, and  $\unicode[STIX]{x1D712}(\mathbf{v})\geqslant r(\mathbf{v})$. If
$\unicode[STIX]{x1D712}(\mathbf{v})\geqslant r(\mathbf{v})$. If  $e=0$, then further suppose
$e=0$, then further suppose  $\unicode[STIX]{x1D712}(\mathbf{v}(-E))<0$ and
$\unicode[STIX]{x1D712}(\mathbf{v}(-E))<0$ and  $\unicode[STIX]{x1D708}(\mathbf{v})\cdot E<0$. The character
$\unicode[STIX]{x1D708}(\mathbf{v})\cdot E<0$. The character  $\mathbf{m}^{D}$ satisfies
$\mathbf{m}^{D}$ satisfies
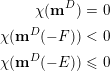 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D712}(\mathbf{m}^{D}) & = & \displaystyle 0\nonumber\\ \displaystyle \unicode[STIX]{x1D712}(\mathbf{m}^{D}(-F)) & {<} & \displaystyle 0\nonumber\\ \displaystyle \unicode[STIX]{x1D712}(\mathbf{m}^{D}(-E)) & {\leqslant} & \displaystyle 0\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D712}(\mathbf{m}^{D}) & = & \displaystyle 0\nonumber\\ \displaystyle \unicode[STIX]{x1D712}(\mathbf{m}^{D}(-F)) & {<} & \displaystyle 0\nonumber\\ \displaystyle \unicode[STIX]{x1D712}(\mathbf{m}^{D}(-E)) & {\leqslant} & \displaystyle 0\nonumber\end{eqnarray}$$ and, if  $e\geqslant 2$, then furthermore
$e\geqslant 2$, then furthermore
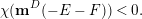 $$\begin{eqnarray}\unicode[STIX]{x1D712}(\mathbf{m}^{D}(-E-F))<0.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D712}(\mathbf{m}^{D}(-E-F))<0.\end{eqnarray}$$Proof. By Serre duality it is equivalent to show
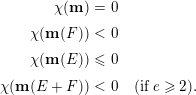 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D712}(\mathbf{m}) & = & \displaystyle 0\nonumber\\ \displaystyle \unicode[STIX]{x1D712}(\mathbf{m}(F)) & {<} & \displaystyle 0\nonumber\\ \displaystyle \unicode[STIX]{x1D712}(\mathbf{m}(E)) & {\leqslant} & \displaystyle 0\nonumber\\ \displaystyle \unicode[STIX]{x1D712}(\mathbf{m}(E+F)) & {<} & \displaystyle 0\quad (\text{if }e\geqslant 2).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D712}(\mathbf{m}) & = & \displaystyle 0\nonumber\\ \displaystyle \unicode[STIX]{x1D712}(\mathbf{m}(F)) & {<} & \displaystyle 0\nonumber\\ \displaystyle \unicode[STIX]{x1D712}(\mathbf{m}(E)) & {\leqslant} & \displaystyle 0\nonumber\\ \displaystyle \unicode[STIX]{x1D712}(\mathbf{m}(E+F)) & {<} & \displaystyle 0\quad (\text{if }e\geqslant 2).\nonumber\end{eqnarray}$$The first statement is clear. For the second, we use Lemma 2.3 to compute
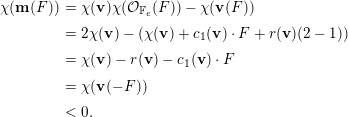 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D712}(\mathbf{m}(F)) & = & \displaystyle \unicode[STIX]{x1D712}(\mathbf{v})\unicode[STIX]{x1D712}({\mathcal{O}}_{\mathbb{F}_{e}}(F))-\unicode[STIX]{x1D712}(\mathbf{v}(F))\nonumber\\ \displaystyle & = & \displaystyle 2\unicode[STIX]{x1D712}(\mathbf{v})-(\unicode[STIX]{x1D712}(\mathbf{v})+c_{1}(\mathbf{v})\cdot F+r(\mathbf{v})(2-1))\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D712}(\mathbf{v})-r(\mathbf{v})-c_{1}(\mathbf{v})\cdot F\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D712}(\mathbf{v}(-F))\nonumber\\ \displaystyle & {<} & \displaystyle 0.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D712}(\mathbf{m}(F)) & = & \displaystyle \unicode[STIX]{x1D712}(\mathbf{v})\unicode[STIX]{x1D712}({\mathcal{O}}_{\mathbb{F}_{e}}(F))-\unicode[STIX]{x1D712}(\mathbf{v}(F))\nonumber\\ \displaystyle & = & \displaystyle 2\unicode[STIX]{x1D712}(\mathbf{v})-(\unicode[STIX]{x1D712}(\mathbf{v})+c_{1}(\mathbf{v})\cdot F+r(\mathbf{v})(2-1))\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D712}(\mathbf{v})-r(\mathbf{v})-c_{1}(\mathbf{v})\cdot F\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D712}(\mathbf{v}(-F))\nonumber\\ \displaystyle & {<} & \displaystyle 0.\nonumber\end{eqnarray}$$ If  $e=0$, then the third inequality follows by symmetry. If instead
$e=0$, then the third inequality follows by symmetry. If instead  $e\geqslant 1$, then
$e\geqslant 1$, then
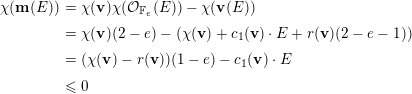 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D712}(\mathbf{m}(E)) & = & \displaystyle \unicode[STIX]{x1D712}(\mathbf{v})\unicode[STIX]{x1D712}({\mathcal{O}}_{\mathbb{F}_{e}}(E))-\unicode[STIX]{x1D712}(\mathbf{v}(E))\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D712}(\mathbf{v})(2-e)-(\unicode[STIX]{x1D712}(\mathbf{v})+c_{1}(\mathbf{v})\cdot E+r(\mathbf{v})(2-e-1))\nonumber\\ \displaystyle & = & \displaystyle (\unicode[STIX]{x1D712}(\mathbf{v})-r(\mathbf{v}))(1-e)-c_{1}(\mathbf{v})\cdot E\nonumber\\ \displaystyle & {\leqslant} & \displaystyle 0\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D712}(\mathbf{m}(E)) & = & \displaystyle \unicode[STIX]{x1D712}(\mathbf{v})\unicode[STIX]{x1D712}({\mathcal{O}}_{\mathbb{F}_{e}}(E))-\unicode[STIX]{x1D712}(\mathbf{v}(E))\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D712}(\mathbf{v})(2-e)-(\unicode[STIX]{x1D712}(\mathbf{v})+c_{1}(\mathbf{v})\cdot E+r(\mathbf{v})(2-e-1))\nonumber\\ \displaystyle & = & \displaystyle (\unicode[STIX]{x1D712}(\mathbf{v})-r(\mathbf{v}))(1-e)-c_{1}(\mathbf{v})\cdot E\nonumber\\ \displaystyle & {\leqslant} & \displaystyle 0\nonumber\end{eqnarray}$$ since  $\unicode[STIX]{x1D712}(\mathbf{v})\geqslant r(\mathbf{v})$ and
$\unicode[STIX]{x1D712}(\mathbf{v})\geqslant r(\mathbf{v})$ and  $c_{1}(\mathbf{v})$ is nef.
$c_{1}(\mathbf{v})$ is nef.
Finally, we similarly compute
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D712}(\mathbf{m}(E+F)) & = & \displaystyle \unicode[STIX]{x1D712}(\mathbf{v})\unicode[STIX]{x1D712}({\mathcal{O}}_{\mathbb{F}_{e}}(E+F))-\unicode[STIX]{x1D712}(\mathbf{v}(E+F))\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D712}(\mathbf{v})(4-e)-(\unicode[STIX]{x1D712}(\mathbf{v})+c_{1}(\mathbf{v})\cdot (E+F)+r(\mathbf{v})(4-e-1))\nonumber\\ \displaystyle & = & \displaystyle (\unicode[STIX]{x1D712}(\mathbf{v})-r(\mathbf{v}))(3-e)-c_{1}(\mathbf{v})\cdot (E+F).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D712}(\mathbf{m}(E+F)) & = & \displaystyle \unicode[STIX]{x1D712}(\mathbf{v})\unicode[STIX]{x1D712}({\mathcal{O}}_{\mathbb{F}_{e}}(E+F))-\unicode[STIX]{x1D712}(\mathbf{v}(E+F))\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D712}(\mathbf{v})(4-e)-(\unicode[STIX]{x1D712}(\mathbf{v})+c_{1}(\mathbf{v})\cdot (E+F)+r(\mathbf{v})(4-e-1))\nonumber\\ \displaystyle & = & \displaystyle (\unicode[STIX]{x1D712}(\mathbf{v})-r(\mathbf{v}))(3-e)-c_{1}(\mathbf{v})\cdot (E+F).\nonumber\end{eqnarray}$$ Since  $\unicode[STIX]{x1D712}(\mathbf{v})\geqslant r(\mathbf{v})$ and
$\unicode[STIX]{x1D712}(\mathbf{v})\geqslant r(\mathbf{v})$ and  $c_{1}(\mathbf{v})$ is nef with
$c_{1}(\mathbf{v})$ is nef with  $c_{1}(\mathbf{v})\cdot F>0$, it follows that
$c_{1}(\mathbf{v})\cdot F>0$, it follows that  $\unicode[STIX]{x1D712}(\mathbf{m}(E+F))<0$ if
$\unicode[STIX]{x1D712}(\mathbf{m}(E+F))<0$ if  $e\geqslant 3$. Suppose
$e\geqslant 3$. Suppose  $e=2$. Then the above expression reduces to
$e=2$. Then the above expression reduces to
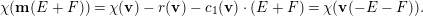 $$\begin{eqnarray}\unicode[STIX]{x1D712}(\mathbf{m}(E+F))=\unicode[STIX]{x1D712}(\mathbf{v})-r(\mathbf{v})-c_{1}(\mathbf{v})\cdot (E+F)=\unicode[STIX]{x1D712}(\mathbf{v}(-E-F)).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D712}(\mathbf{m}(E+F))=\unicode[STIX]{x1D712}(\mathbf{v})-r(\mathbf{v})-c_{1}(\mathbf{v})\cdot (E+F)=\unicode[STIX]{x1D712}(\mathbf{v}(-E-F)).\end{eqnarray}$$ Let  ${\mathcal{V}}\in {\mathcal{P}}_{F}(\mathbf{v})$ be general. Then
${\mathcal{V}}\in {\mathcal{P}}_{F}(\mathbf{v})$ be general. Then  ${\mathcal{V}}(-F)$ only has
${\mathcal{V}}(-F)$ only has  $h^{1}$, and
$h^{1}$, and  ${\mathcal{V}}(-F)|_{E}$ splits as a direct sum of line bundles of degree
${\mathcal{V}}(-F)|_{E}$ splits as a direct sum of line bundles of degree  ${\geqslant}-1$. Then the restriction sequence
${\geqslant}-1$. Then the restriction sequence
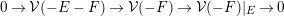 $$\begin{eqnarray}0\rightarrow {\mathcal{V}}(-E-F)\rightarrow {\mathcal{V}}(-F)\rightarrow {\mathcal{V}}(-F)|_{E}\rightarrow 0\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow {\mathcal{V}}(-E-F)\rightarrow {\mathcal{V}}(-F)\rightarrow {\mathcal{V}}(-F)|_{E}\rightarrow 0\end{eqnarray}$$ shows that the only nonzero cohomology of  ${\mathcal{V}}(-E-F)$ is also
${\mathcal{V}}(-E-F)$ is also  $h^{1}(\mathbb{F}_{e},{\mathcal{V}}(-E-F))\neq 0$, and therefore
$h^{1}(\mathbb{F}_{e},{\mathcal{V}}(-E-F))\neq 0$, and therefore  $\unicode[STIX]{x1D712}(\mathbf{v}(-E-F))<0$ as required.◻
$\unicode[STIX]{x1D712}(\mathbf{v}(-E-F))<0$ as required.◻
Together with the other results in this section, the next result completes the classification and proves Theorems 5.1 and 5.2.
Proposition 5.10. Suppose  $\unicode[STIX]{x1D712}(\mathbf{v}(-F))<0$,
$\unicode[STIX]{x1D712}(\mathbf{v}(-F))<0$,  $\unicode[STIX]{x1D708}(\mathbf{v})\cdot F>0$, and
$\unicode[STIX]{x1D708}(\mathbf{v})\cdot F>0$, and  $\unicode[STIX]{x1D712}(\mathbf{v})\geqslant r(\mathbf{v})+2$. If
$\unicode[STIX]{x1D712}(\mathbf{v})\geqslant r(\mathbf{v})+2$. If  $e=0$, further assume
$e=0$, further assume  $\unicode[STIX]{x1D712}(\mathbf{v}(-E))<0$ and
$\unicode[STIX]{x1D712}(\mathbf{v}(-E))<0$ and  $\unicode[STIX]{x1D708}(\mathbf{v})\cdot E>0$. Then
$\unicode[STIX]{x1D708}(\mathbf{v})\cdot E>0$. Then  $\mathbf{v}$ is globally generated.
$\mathbf{v}$ is globally generated.
Proof. First assume  $\unicode[STIX]{x1D712}(\mathbf{m}^{D}(-E-F))<0$. Then by Lemma 5.9,
$\unicode[STIX]{x1D712}(\mathbf{m}^{D}(-E-F))<0$. Then by Lemma 5.9,  ${\mathcal{O}}_{\mathbb{F}_{e}}$ is a line bundle satisfying the inequalities (
${\mathcal{O}}_{\mathbb{F}_{e}}$ is a line bundle satisfying the inequalities ( $\dagger$) for the character
$\dagger$) for the character  $\mathbf{m}^{D}$. Therefore, by Proposition 4.4, the stack
$\mathbf{m}^{D}$. Therefore, by Proposition 4.4, the stack  ${\mathcal{P}}_{F}(\mathbf{m}^{D})$ is nonempty and a general
${\mathcal{P}}_{F}(\mathbf{m}^{D})$ is nonempty and a general  ${\mathcal{M}}^{D}\in {\mathcal{P}}_{F}(\mathbf{m}^{D})$ admits a resolution of the form
${\mathcal{M}}^{D}\in {\mathcal{P}}_{F}(\mathbf{m}^{D})$ admits a resolution of the form
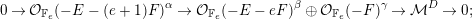 $$\begin{eqnarray}0\rightarrow {\mathcal{O}}_{\mathbb{F}_{e}}(-E-(e+1)F)^{\unicode[STIX]{x1D6FC}}\rightarrow {\mathcal{O}}_{\mathbb{F}_{e}}(-E-eF)^{\unicode[STIX]{x1D6FD}}\oplus {\mathcal{O}}_{\mathbb{F}_{e}}(-F)^{\unicode[STIX]{x1D6FE}}\rightarrow {\mathcal{M}}^{D}\rightarrow 0;\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow {\mathcal{O}}_{\mathbb{F}_{e}}(-E-(e+1)F)^{\unicode[STIX]{x1D6FC}}\rightarrow {\mathcal{O}}_{\mathbb{F}_{e}}(-E-eF)^{\unicode[STIX]{x1D6FD}}\oplus {\mathcal{O}}_{\mathbb{F}_{e}}(-F)^{\unicode[STIX]{x1D6FE}}\rightarrow {\mathcal{M}}^{D}\rightarrow 0;\end{eqnarray}$$ there are no copies of  ${\mathcal{O}}_{\mathbb{F}_{e}}$ in the resolution since
${\mathcal{O}}_{\mathbb{F}_{e}}$ in the resolution since  $\unicode[STIX]{x1D712}(\mathbf{m}^{D})=0$. Since
$\unicode[STIX]{x1D712}(\mathbf{m}^{D})=0$. Since  $\unicode[STIX]{x1D712}(\mathbf{v})\geqslant r(\mathbf{v})+2$, we have
$\unicode[STIX]{x1D712}(\mathbf{v})\geqslant r(\mathbf{v})+2$, we have  $r({\mathcal{M}}^{D})\geqslant 2$ and therefore, by Theorem 2.5,
$r({\mathcal{M}}^{D})\geqslant 2$ and therefore, by Theorem 2.5,  ${\mathcal{M}}^{D}$ is a vector bundle. Clearly
${\mathcal{M}}^{D}$ is a vector bundle. Clearly  ${\mathcal{M}}^{D}$ has no cohomology, so its Serre dual
${\mathcal{M}}^{D}$ has no cohomology, so its Serre dual  ${\mathcal{M}}$ also has no cohomology. The bundle
${\mathcal{M}}$ also has no cohomology. The bundle  ${\mathcal{M}}$ fits in a sequence
${\mathcal{M}}$ fits in a sequence
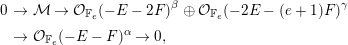 $$\begin{eqnarray}\displaystyle 0 & \rightarrow & \displaystyle {\mathcal{M}}\rightarrow {\mathcal{O}}_{\mathbb{F}_{e}}(-E-2F)^{\unicode[STIX]{x1D6FD}}\oplus {\mathcal{O}}_{\mathbb{F}_{e}}(-2E-(e+1)F)^{\unicode[STIX]{x1D6FE}}\nonumber\\ \displaystyle & \rightarrow & \displaystyle {\mathcal{O}}_{\mathbb{F}_{e}}(-E-F)^{\unicode[STIX]{x1D6FC}}\rightarrow 0,\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 0 & \rightarrow & \displaystyle {\mathcal{M}}\rightarrow {\mathcal{O}}_{\mathbb{F}_{e}}(-E-2F)^{\unicode[STIX]{x1D6FD}}\oplus {\mathcal{O}}_{\mathbb{F}_{e}}(-2E-(e+1)F)^{\unicode[STIX]{x1D6FE}}\nonumber\\ \displaystyle & \rightarrow & \displaystyle {\mathcal{O}}_{\mathbb{F}_{e}}(-E-F)^{\unicode[STIX]{x1D6FC}}\rightarrow 0,\nonumber\end{eqnarray}$$ from which it immediately follows that  $h^{1}(\mathbb{F}_{e},{\mathcal{M}}(-F))=0$. The dual
$h^{1}(\mathbb{F}_{e},{\mathcal{M}}(-F))=0$. The dual  ${\mathcal{M}}^{\ast }$ has a resolution
${\mathcal{M}}^{\ast }$ has a resolution
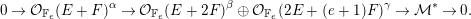 $$\begin{eqnarray}0\rightarrow {\mathcal{O}}_{\mathbb{F}_{e}}(E+F)^{\unicode[STIX]{x1D6FC}}\rightarrow {\mathcal{O}}_{\mathbb{F}_{e}}(E+2F)^{\unicode[STIX]{x1D6FD}}\oplus {\mathcal{O}}_{\mathbb{F}_{e}}(2E+(e+1)F)^{\unicode[STIX]{x1D6FE}}\rightarrow {\mathcal{M}}^{\ast }\rightarrow 0.\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow {\mathcal{O}}_{\mathbb{F}_{e}}(E+F)^{\unicode[STIX]{x1D6FC}}\rightarrow {\mathcal{O}}_{\mathbb{F}_{e}}(E+2F)^{\unicode[STIX]{x1D6FD}}\oplus {\mathcal{O}}_{\mathbb{F}_{e}}(2E+(e+1)F)^{\unicode[STIX]{x1D6FE}}\rightarrow {\mathcal{M}}^{\ast }\rightarrow 0.\end{eqnarray}$$ The line bundles  ${\mathcal{O}}_{\mathbb{F}_{e}}(E+2F)$ and
${\mathcal{O}}_{\mathbb{F}_{e}}(E+2F)$ and  ${\mathcal{O}}_{\mathbb{F}_{e}}(2E+(e+1)F)$ are each globally generated at all points
${\mathcal{O}}_{\mathbb{F}_{e}}(2E+(e+1)F)$ are each globally generated at all points  $p\in \mathbb{F}_{e}$ with
$p\in \mathbb{F}_{e}$ with  $p\notin E$, and therefore
$p\notin E$, and therefore  ${\mathcal{M}}^{\ast }$ is globally generated away from
${\mathcal{M}}^{\ast }$ is globally generated away from  $E$.
$E$.
To see that  ${\mathcal{M}}^{\ast }$ is globally generated at all points on
${\mathcal{M}}^{\ast }$ is globally generated at all points on  $E$, observe that
$E$, observe that  $c_{1}({\mathcal{M}}^{\ast })=c_{1}(\mathbf{v})$ is nef, so in particular
$c_{1}({\mathcal{M}}^{\ast })=c_{1}(\mathbf{v})$ is nef, so in particular  $c_{1}({\mathcal{M}}^{\ast })\cdot E\geqslant 0$. The resolution of
$c_{1}({\mathcal{M}}^{\ast })\cdot E\geqslant 0$. The resolution of  ${\mathcal{M}}^{\ast }$ shows that
${\mathcal{M}}^{\ast }$ shows that  $h^{1}(\mathbb{F}_{e},{\mathcal{M}}^{\ast }(-E))=0$. If
$h^{1}(\mathbb{F}_{e},{\mathcal{M}}^{\ast }(-E))=0$. If  ${\mathcal{M}}^{\ast }|_{E}$ splits as a balanced direct sum of line bundles, then
${\mathcal{M}}^{\ast }|_{E}$ splits as a balanced direct sum of line bundles, then  ${\mathcal{M}}^{\ast }|_{E}$ is globally generated and the restriction sequence
${\mathcal{M}}^{\ast }|_{E}$ is globally generated and the restriction sequence
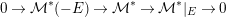 $$\begin{eqnarray}0\rightarrow {\mathcal{M}}^{\ast }(-E)\rightarrow {\mathcal{M}}^{\ast }\rightarrow {\mathcal{M}}^{\ast }|_{E}\rightarrow 0\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow {\mathcal{M}}^{\ast }(-E)\rightarrow {\mathcal{M}}^{\ast }\rightarrow {\mathcal{M}}^{\ast }|_{E}\rightarrow 0\end{eqnarray}$$ shows that  ${\mathcal{M}}^{\ast }$ is globally generated on
${\mathcal{M}}^{\ast }$ is globally generated on  $E$. By Proposition 2.6, to see
$E$. By Proposition 2.6, to see  ${\mathcal{M}}^{\ast }|_{E}$ is balanced (for a general
${\mathcal{M}}^{\ast }|_{E}$ is balanced (for a general  ${\mathcal{M}}^{\ast }$) it is enough to show
${\mathcal{M}}^{\ast }$) it is enough to show  ${\mathcal{M}}^{D}$ (and hence
${\mathcal{M}}^{D}$ (and hence  ${\mathcal{M}}^{\ast }$) is
${\mathcal{M}}^{\ast }$) is  $E$-prioritary. To see
$E$-prioritary. To see  $\operatorname{Ext}^{2}({\mathcal{M}}^{D},{\mathcal{M}}^{D}(-E))=0,$ it is enough to verify
$\operatorname{Ext}^{2}({\mathcal{M}}^{D},{\mathcal{M}}^{D}(-E))=0,$ it is enough to verify  $\operatorname{Ext}^{2}({\mathcal{M}}^{D},{\mathcal{O}}_{\mathbb{F}_{e}}(-2E-eF))=\operatorname{Ext}^{2}({\mathcal{M}}^{D},{\mathcal{O}}_{\mathbb{F}_{e}}(-E-F))=0$. Equivalently by Serre duality, we need
$\operatorname{Ext}^{2}({\mathcal{M}}^{D},{\mathcal{O}}_{\mathbb{F}_{e}}(-2E-eF))=\operatorname{Ext}^{2}({\mathcal{M}}^{D},{\mathcal{O}}_{\mathbb{F}_{e}}(-E-F))=0$. Equivalently by Serre duality, we need
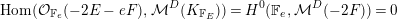 $$\begin{eqnarray}\operatorname{Hom}({\mathcal{O}}_{\mathbb{F}_{e}}(-2E-eF),{\mathcal{M}}^{D}(K_{\mathbb{ F}_{E}}))=H^{0}(\mathbb{F}_{e},{\mathcal{M}}^{D}(-2F))=0\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Hom}({\mathcal{O}}_{\mathbb{F}_{e}}(-2E-eF),{\mathcal{M}}^{D}(K_{\mathbb{ F}_{E}}))=H^{0}(\mathbb{F}_{e},{\mathcal{M}}^{D}(-2F))=0\end{eqnarray}$$and
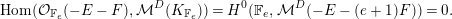 $$\begin{eqnarray}\operatorname{Hom}({\mathcal{O}}_{\mathbb{F}_{e}}(-E-F),{\mathcal{M}}^{D}(K_{\mathbb{ F}_{e}}))=H^{0}(\mathbb{F}_{e},{\mathcal{M}}^{D}(-E-(e+1)F))=0.\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Hom}({\mathcal{O}}_{\mathbb{F}_{e}}(-E-F),{\mathcal{M}}^{D}(K_{\mathbb{ F}_{e}}))=H^{0}(\mathbb{F}_{e},{\mathcal{M}}^{D}(-E-(e+1)F))=0.\end{eqnarray}$$ Both vanishings follow immediately from the resolution of  ${\mathcal{M}}^{D}$. Therefore,
${\mathcal{M}}^{D}$. Therefore,  ${\mathcal{M}}^{\ast }$ is globally generated, and Lemma 5.7 completes the proof in case
${\mathcal{M}}^{\ast }$ is globally generated, and Lemma 5.7 completes the proof in case  $\unicode[STIX]{x1D712}(\mathbf{m}^{D}(-E-F))<0$.
$\unicode[STIX]{x1D712}(\mathbf{m}^{D}(-E-F))<0$.
Finally suppose  $\unicode[STIX]{x1D712}(\mathbf{m}^{D}(-E-F))\geqslant 0$. By Lemma 5.9, we must have
$\unicode[STIX]{x1D712}(\mathbf{m}^{D}(-E-F))\geqslant 0$. By Lemma 5.9, we must have  $e\in \{0,1\}$. Define integers
$e\in \{0,1\}$. Define integers
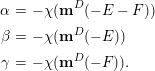 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FC} & = & \displaystyle -\unicode[STIX]{x1D712}(\mathbf{m}^{D}(-E-F))\nonumber\\ \displaystyle \unicode[STIX]{x1D6FD} & = & \displaystyle -\unicode[STIX]{x1D712}(\mathbf{m}^{D}(-E))\nonumber\\ \displaystyle \unicode[STIX]{x1D6FE} & = & \displaystyle -\unicode[STIX]{x1D712}(\mathbf{m}^{D}(-F)).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FC} & = & \displaystyle -\unicode[STIX]{x1D712}(\mathbf{m}^{D}(-E-F))\nonumber\\ \displaystyle \unicode[STIX]{x1D6FD} & = & \displaystyle -\unicode[STIX]{x1D712}(\mathbf{m}^{D}(-E))\nonumber\\ \displaystyle \unicode[STIX]{x1D6FE} & = & \displaystyle -\unicode[STIX]{x1D712}(\mathbf{m}^{D}(-F)).\nonumber\end{eqnarray}$$ By Lemma, 5.9, we have  $\unicode[STIX]{x1D6FC}\leqslant 0$,
$\unicode[STIX]{x1D6FC}\leqslant 0$,  $\unicode[STIX]{x1D6FD}\geqslant 0$, and
$\unicode[STIX]{x1D6FD}\geqslant 0$, and  $\unicode[STIX]{x1D6FE}>0$. Then the direct sum of line bundles
$\unicode[STIX]{x1D6FE}>0$. Then the direct sum of line bundles
 $$\begin{eqnarray}{\mathcal{M}}^{D}:={\mathcal{O}}_{\mathbb{ F}_{e}}(-E-(e+1)F)^{-\unicode[STIX]{x1D6FC}}\oplus {\mathcal{O}}_{\mathbb{F}_{e}}(-E-eF)^{\unicode[STIX]{x1D6FD}}\oplus {\mathcal{O}}_{\mathbb{ F}_{e}}(-F)^{\unicode[STIX]{x1D6FE}}\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{M}}^{D}:={\mathcal{O}}_{\mathbb{ F}_{e}}(-E-(e+1)F)^{-\unicode[STIX]{x1D6FC}}\oplus {\mathcal{O}}_{\mathbb{F}_{e}}(-E-eF)^{\unicode[STIX]{x1D6FD}}\oplus {\mathcal{O}}_{\mathbb{ F}_{e}}(-F)^{\unicode[STIX]{x1D6FE}}\end{eqnarray}$$ has  $\operatorname{ch}({\mathcal{M}}^{D})=\mathbf{m}^{D}$ by an argument analogous to the first part of the proof of Proposition 4.4. Its Serre dual is the bundle
$\operatorname{ch}({\mathcal{M}}^{D})=\mathbf{m}^{D}$ by an argument analogous to the first part of the proof of Proposition 4.4. Its Serre dual is the bundle
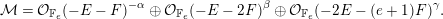 $$\begin{eqnarray}{\mathcal{M}}={\mathcal{O}}_{\mathbb{F}_{e}}(-E-F)^{-\unicode[STIX]{x1D6FC}}\oplus {\mathcal{O}}_{\mathbb{F}_{e}}(-E-2F)^{\unicode[STIX]{x1D6FD}}\oplus {\mathcal{O}}_{\mathbb{ F}_{e}}(-2E-(e+1)F)^{\unicode[STIX]{x1D6FE}}.\end{eqnarray}$$
$$\begin{eqnarray}{\mathcal{M}}={\mathcal{O}}_{\mathbb{F}_{e}}(-E-F)^{-\unicode[STIX]{x1D6FC}}\oplus {\mathcal{O}}_{\mathbb{F}_{e}}(-E-2F)^{\unicode[STIX]{x1D6FD}}\oplus {\mathcal{O}}_{\mathbb{ F}_{e}}(-2E-(e+1)F)^{\unicode[STIX]{x1D6FE}}.\end{eqnarray}$$ Then  ${\mathcal{M}}$ has no cohomology,
${\mathcal{M}}$ has no cohomology,  $h^{1}(\mathbb{F}_{e},{\mathcal{M}}(-F))=0$, and
$h^{1}(\mathbb{F}_{e},{\mathcal{M}}(-F))=0$, and  ${\mathcal{M}}^{\ast }$ is globally generated (since
${\mathcal{M}}^{\ast }$ is globally generated (since  $e\leqslant 1$). By Lemma 5.7,
$e\leqslant 1$). By Lemma 5.7,  $\mathbf{v}$ is globally generated.◻
$\mathbf{v}$ is globally generated.◻
5.4 Notes on ampleness
We close the paper with some remarks on the question that initially led us to study globally generated vector bundles. Let  $X$ be a smooth surface. Recall that a vector bundle
$X$ be a smooth surface. Recall that a vector bundle  ${\mathcal{V}}$ on
${\mathcal{V}}$ on  $X$ is ample if the line bundle
$X$ is ample if the line bundle  ${\mathcal{O}}_{\mathbb{P}{\mathcal{V}}}(1)$ is ample.
${\mathcal{O}}_{\mathbb{P}{\mathcal{V}}}(1)$ is ample.
Problem 5.11. Classify the Chern characters of ample vector bundles on  $X$.
$X$.
On  $\mathbb{P}^{2}$ and
$\mathbb{P}^{2}$ and  $\mathbb{F}_{e}$, ample line bundles are globally generated. In contrast, examples of Gieseker show that higher rank ample vector bundles need not have any sections. For example, a bundle
$\mathbb{F}_{e}$, ample line bundles are globally generated. In contrast, examples of Gieseker show that higher rank ample vector bundles need not have any sections. For example, a bundle  ${\mathcal{V}}$ defined by a general resolution of the form
${\mathcal{V}}$ defined by a general resolution of the form
 $$\begin{eqnarray}0\rightarrow {\mathcal{O}}_{\mathbb{P}^{2}}(-d)^{2}\rightarrow {\mathcal{O}}_{\mathbb{P}^{2}}(-1)^{4}\rightarrow {\mathcal{V}}\rightarrow 0\end{eqnarray}$$
$$\begin{eqnarray}0\rightarrow {\mathcal{O}}_{\mathbb{P}^{2}}(-d)^{2}\rightarrow {\mathcal{O}}_{\mathbb{P}^{2}}(-1)^{4}\rightarrow {\mathcal{V}}\rightarrow 0\end{eqnarray}$$ is ample provided  $d\gg 0$ (see [Reference LazarsfeldLaz04, Example 6.3.17] or [Reference GiesekerGie71]). However, if a vector bundle
$d\gg 0$ (see [Reference LazarsfeldLaz04, Example 6.3.17] or [Reference GiesekerGie71]). However, if a vector bundle  ${\mathcal{V}}$ is ample, then
${\mathcal{V}}$ is ample, then  $\operatorname{Sym}^{k}{\mathcal{V}}$ has no higher cohomology and is globally generated for sufficiently large
$\operatorname{Sym}^{k}{\mathcal{V}}$ has no higher cohomology and is globally generated for sufficiently large  $k$. By Riemann–Roch this implies the necessary inequality (see also [Reference Fulton and LazarsfeldFL83])
$k$. By Riemann–Roch this implies the necessary inequality (see also [Reference Fulton and LazarsfeldFL83])
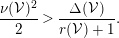 $$\begin{eqnarray}\frac{\unicode[STIX]{x1D708}({\mathcal{V}})^{2}}{2}>\frac{\unicode[STIX]{x1D6E5}({\mathcal{V}})}{r({\mathcal{V}})+1}.\end{eqnarray}$$
$$\begin{eqnarray}\frac{\unicode[STIX]{x1D708}({\mathcal{V}})^{2}}{2}>\frac{\unicode[STIX]{x1D6E5}({\mathcal{V}})}{r({\mathcal{V}})+1}.\end{eqnarray}$$ Furthermore,  $\unicode[STIX]{x1D708}({\mathcal{V}})$ needs to be ample and its restriction to any curve needs to be ample. On
$\unicode[STIX]{x1D708}({\mathcal{V}})$ needs to be ample and its restriction to any curve needs to be ample. On  $\mathbb{F}_{e}$, this implies that
$\mathbb{F}_{e}$, this implies that  $\unicode[STIX]{x1D708}({\mathcal{V}})\cdot E\geqslant 1$ and
$\unicode[STIX]{x1D708}({\mathcal{V}})\cdot E\geqslant 1$ and  $\unicode[STIX]{x1D708}({\mathcal{V}})\cdot F\geqslant 1.$ If
$\unicode[STIX]{x1D708}({\mathcal{V}})\cdot F\geqslant 1.$ If  $\unicode[STIX]{x1D708}({\mathcal{V}})\cdot F=1$, the restriction of the bundle to every fiber must be
$\unicode[STIX]{x1D708}({\mathcal{V}})\cdot F=1$, the restriction of the bundle to every fiber must be  ${\mathcal{O}}_{\mathbb{P}^{1}}(1)^{r}$, and hence
${\mathcal{O}}_{\mathbb{P}^{1}}(1)^{r}$, and hence  ${\mathcal{V}}(-E)$ is pulled back from
${\mathcal{V}}(-E)$ is pulled back from  $\mathbb{P}^{1}$. One can ask whether the inequality (*) suffices to show a general
$\mathbb{P}^{1}$. One can ask whether the inequality (*) suffices to show a general  ${\mathcal{V}}$ is ample if
${\mathcal{V}}$ is ample if  $\unicode[STIX]{x1D708}({\mathcal{V}})$ is sufficiently ample. For the Gieseker example above, the inequality (*) implies that if
$\unicode[STIX]{x1D708}({\mathcal{V}})$ is sufficiently ample. For the Gieseker example above, the inequality (*) implies that if  ${\mathcal{V}}$ is ample, then
${\mathcal{V}}$ is ample, then  $d\geqslant 7$. The authors do not know the optimal value of
$d\geqslant 7$. The authors do not know the optimal value of  $d$ for
$d$ for  ${\mathcal{V}}$ to be ample even in this case.
${\mathcal{V}}$ to be ample even in this case.
By the next simple observation, our characterization of globally generated characters on  $\mathbb{F}_{e}$ yields sufficient conditions for a character to be the character of an ample bundle. However, analogues of Gieseker’s example (see [Reference LazarsfeldLaz04, Theorem 6.3.65]) show that these conditions are certainly not necessary.
$\mathbb{F}_{e}$ yields sufficient conditions for a character to be the character of an ample bundle. However, analogues of Gieseker’s example (see [Reference LazarsfeldLaz04, Theorem 6.3.65]) show that these conditions are certainly not necessary.
Lemma 5.12. Let  $X$ be a projective variety with an ample divisor
$X$ be a projective variety with an ample divisor  $H$. Suppose
$H$. Suppose  ${\mathcal{V}}$ is a vector bundle on
${\mathcal{V}}$ is a vector bundle on  $X$ such that
$X$ such that  ${\mathcal{V}}(-H)$ is globally generated. Then
${\mathcal{V}}(-H)$ is globally generated. Then  ${\mathcal{V}}$ is ample.
${\mathcal{V}}$ is ample.
Proof. As  ${\mathcal{V}}(-H)$ is a quotient of
${\mathcal{V}}(-H)$ is a quotient of  ${\mathcal{O}}_{X}^{n}$, we find that
${\mathcal{O}}_{X}^{n}$, we find that  ${\mathcal{V}}$ is the quotient of an ample bundle.◻
${\mathcal{V}}$ is the quotient of an ample bundle.◻
On  $\mathbb{F}_{e}$, we take
$\mathbb{F}_{e}$, we take  $H=E+(e+1)F$ and deduce the following result.
$H=E+(e+1)F$ and deduce the following result.
Corollary 5.13. Suppose  $e\geqslant 2$, and let
$e\geqslant 2$, and let  $\mathbf{v}\in K(\mathbb{F}_{e})$ be a Chern character such that
$\mathbf{v}\in K(\mathbb{F}_{e})$ be a Chern character such that  $r(\mathbf{v})\geqslant 2$,
$r(\mathbf{v})\geqslant 2$,  $\unicode[STIX]{x1D6E5}(\mathbf{v})\geqslant 0$,
$\unicode[STIX]{x1D6E5}(\mathbf{v})\geqslant 0$,  $\unicode[STIX]{x1D708}(\mathbf{v})\cdot F\geqslant 1$, and
$\unicode[STIX]{x1D708}(\mathbf{v})\cdot F\geqslant 1$, and  $\unicode[STIX]{x1D708}(\mathbf{v})\cdot E\geqslant 1$. Then the general
$\unicode[STIX]{x1D708}(\mathbf{v})\cdot E\geqslant 1$. Then the general  ${\mathcal{V}}\in {\mathcal{P}}_{F}(\mathbf{v})$ is ample whenever any of the following conditions holds.
${\mathcal{V}}\in {\mathcal{P}}_{F}(\mathbf{v})$ is ample whenever any of the following conditions holds.
(1) We have
 $\unicode[STIX]{x1D708}(\mathbf{v})\cdot F=1$, and there are integers
$\unicode[STIX]{x1D708}(\mathbf{v})\cdot F=1$, and there are integers  $a,m\geqslant 0$ such that
$a,m\geqslant 0$ such that  $$\begin{eqnarray}\displaystyle \mathbf{v} & = & \displaystyle (r(\mathbf{v})-m)\operatorname{ch}{\mathcal{O}}_{\mathbb{F}_{e}}(E+(e+a+1)F)\nonumber\\ \displaystyle & & \displaystyle +\,m\operatorname{ch}{\mathcal{O}}_{\mathbb{F}_{e}}(E+(e+a+2)F).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathbf{v} & = & \displaystyle (r(\mathbf{v})-m)\operatorname{ch}{\mathcal{O}}_{\mathbb{F}_{e}}(E+(e+a+1)F)\nonumber\\ \displaystyle & & \displaystyle +\,m\operatorname{ch}{\mathcal{O}}_{\mathbb{F}_{e}}(E+(e+a+2)F).\nonumber\end{eqnarray}$$(2) We have
 $\unicode[STIX]{x1D708}(\mathbf{v})\cdot F>1$ and
$\unicode[STIX]{x1D708}(\mathbf{v})\cdot F>1$ and  $\unicode[STIX]{x1D712}(\mathbf{v}(-E-(e+2)F))\geqslant 0$.
$\unicode[STIX]{x1D712}(\mathbf{v}(-E-(e+2)F))\geqslant 0$.(3) We have
 $\unicode[STIX]{x1D708}(\mathbf{v})\cdot F>1$,
$\unicode[STIX]{x1D708}(\mathbf{v})\cdot F>1$,  $\unicode[STIX]{x1D712}(\mathbf{v}(-E-(e+2)F))<0$, and
$\unicode[STIX]{x1D712}(\mathbf{v}(-E-(e+2)F))<0$, and  $\unicode[STIX]{x1D712}(\mathbf{v}(-E-(e+1)F))\geqslant r(\mathbf{v})+2$.
$\unicode[STIX]{x1D712}(\mathbf{v}(-E-(e+1)F))\geqslant r(\mathbf{v})+2$.
We leave the analogous statements for  $\mathbb{P}^{1}\times \mathbb{P}^{1}$,
$\mathbb{P}^{1}\times \mathbb{P}^{1}$,  $\mathbb{F}_{1}$, and
$\mathbb{F}_{1}$, and  $\mathbb{P}^{2}$ to the reader. Completing the classification of characters of ample vector bundles remains a very interesting open question for any of these surfaces.
$\mathbb{P}^{2}$ to the reader. Completing the classification of characters of ample vector bundles remains a very interesting open question for any of these surfaces.
Acknowledgments
We would like to thank Aaron Bertram, Lawrence Ein, John Lesieutre, and Daniel Levine for useful discussions.




























































































































































































