Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Ghezzi, L.
Goto, S.
Hong, J.
Ozeki, K.
Phuong, T.T.
and
Vasconcelos, W.V.
2012.
Variation of the first Hilbert coefficients of parameters with a common integral closure.
Journal of Pure and Applied Algebra,
Vol. 216,
Issue. 1,
p.
216.
Goto, Shiro
Hong, Jooyoun
and
Vasconcelos, Wolmer V.
2012.
The homology of parameter ideals.
Journal of Algebra,
Vol. 368,
Issue. ,
p.
271.
Cuong, Nguyen Tu
Goto, Shiro
and
Truong, Hoang Le
2013.
The equalityI2=qIin sequentially Cohen–Macaulay rings.
Journal of Algebra,
Vol. 379,
Issue. ,
p.
50.
Ghezzi, Laura
Goto, Shiro
Hong, Jooyoun
and
Vasconcelos, Wolmer
2013.
Variation of Hilbert coefficients.
Proceedings of the American Mathematical Society,
Vol. 141,
Issue. 9,
p.
3037.
Goto, Shiro
and
Ozeki, Kazuho
2014.
The first Euler characteristics versus the homological degrees.
Bulletin of the Brazilian Mathematical Society, New Series,
Vol. 45,
Issue. 4,
p.
679.
Ghezzi, L.
Goto, S.
Hong, J.
Ozeki, K.
Phuong, T. T.
and
Vasconcelos, W. V.
2015.
The Chern Numbers and Euler Characteristics of Modules.
Acta Mathematica Vietnamica,
Vol. 40,
Issue. 1,
p.
37.

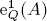 of
of 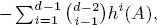 where
where 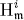 of
of 