Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-13T05:40:33.775Z Has data issue: false hasContentIssue false
  • English
  • Français

The Carathéodory–Cartan–Kaup–Wu Theorem on an Infinite-Dimensional Hilbert Space

Published online by Cambridge University Press:  11 January 2016

Joseph A. Cima ,
Ian Graham ,
Kang Tae Kim  and
Steven G. Krantz
Joseph A. Cima
Affiliation:
Department of Mathematics, University of North Carolina, Chapel Hill, North Carolina 27514, USA, cima@math.unc.edu
Ian Graham
Affiliation:
Department of Mathematics, University of Toronto, Toronto, CANADA M5S 3G3, graham@math.toronto.edu
Kang Tae Kim
Affiliation:
Department of Mathematics, Pohang University of Science and Technology, Pohang 790-784, Koreakimkt@postech.ac.kr
Steven G. Krantz
Affiliation:
Department of Mathematics, Campus Box 1146 Washington University in St. Louis St. Louis, Missouri 63130, USAsk@math.wustl.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This paper treats a holomorphic self-mapping f: Ω → Ω of a bounded domain Ω in a separable Hilbert space 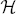with a fixed point p. In case the domain is convex, we prove an infinite-dimensional version of the Cartan-Carathéodory-Kaup-Wu Theorem. This is basically a rigidity result in the vein of the uniqueness part of the classical Schwarz lemma. The main technique, inspired by an old idea of H. Cartan, is iteration of the mapping f and its derivative. A normality result for holomorphic mappings in the compact-weak-open topology, due to Kim and Krantz, is used.

Keywords

46G2032H50
Type
Research Article
Information
Nagoya Mathematical Journal , Volume 185 , 2007 , pp. 17 - 30
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 2007

References

[BOM] Bochner, S. and Martin, W. T., Functions of Several Complex Variables, Princeton University Press, Princeton, 1936.Google Scholar
[CON] Conway, J. B., A Course in Operator Theory, American Mathematical Society, Providence, RI, 2000.Google Scholar
[DAV] Davidson, K. R., C*-algebras by example, Fields Institute Monographs, American Mathematical Society, Providence, RI, 1996.Google Scholar
[DIN] Dineen, S., The Schwarz Lemma, The Clarendon Press, Oxford University Press, Oxford, 1989.Google Scholar
[DUS] Dunford, N. and Schwartz, J. T., Linear Operators, Interscience, New York, 1988.Google Scholar
[FRV] Franzoni, T. and Vesentini, E., Holomorphic Maps and Invariant Distances, North-Holland, Amsterdam, 1980.Google Scholar
[GRK] Greene, R. E. and Krantz, S. G., Characterization of complex manifolds by the isotropy subgroups of their automorphism groups, Indiana Univ. Math. J., 34 (1985), 865–879.CrossRefGoogle Scholar
[HER] Herrero, D.A., Triangular operators, Bull. London Math. Soc., 23 (1991), 513–554.CrossRefGoogle Scholar
[HIP] Hille, E. and Phillips, R. S., Functional Analysis and Semigroups, Amer. Math. Soc. Coll. Publ. 31, Providence, R. I., 1957.Google Scholar
[HUY] Hu, C.-G. and Yue, T. -H., Normal families of holomorphic mappings, J. Math. Anal. Appl., 171 (1992), 436–447.CrossRefGoogle Scholar
[KIK1] Kim, K.-T. and Krantz, S. G., Characerization of the Hilbert ball by its automorphism group, Trans. Amer. Math. Soc., 354 (2002), 2797–2818.CrossRefGoogle Scholar
[KIK2] Kim, K.-T. and Krantz, S. G., Normal families of holomorphic functions and mappings on a Banach space, Expo. Math., 21 (2003), 193–218.CrossRefGoogle Scholar
[KRA] Krantz, S. G., Function Theory of Several Complex Variables, American Mathematical Society-Chelsea, Providence, RI, 2001.CrossRefGoogle Scholar
[LEM] Lempert, L., The Dolbeault complex in infinite dimensions, J. Amer. Math. Soc., 11 (1998), 485–520.CrossRefGoogle Scholar
[MUJ] Mujica, J., Complex Analysis in Banach Spaces, North-Holland, Amsterdam and New York, 1986.Google Scholar
[NAR] Narasimhan, R., Several Complex Variables, University of Chicago Press, Chicago, 1971.Google Scholar
[WU] Wu, H. H., Normal families of holomorphic mappings, Acta Math., 119 (1967), 193–233.CrossRefGoogle Scholar