Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-13T02:47:10.821Z Has data issue: false hasContentIssue false
  • English
  • Français

Cauchy transforms on polynomial curves and related operators

Published online by Cambridge University Press:  22 January 2016

Hyeonbae Kang  and
Jin Keun Seo
Hyeonbae Kang
Affiliation:
Department of Mathematics, Korea University, Seoul 136-701, Korea e-mail: kang@kuccnx.korea.ac.kr
Jin Keun Seo*
Affiliation:
Department of Mathematics, POSTECH, P. O. Box 125, Pohang 790-600, Korea e-mail: seoj@posmath.postech.ac.kr
*
Department of Mathematics, Yonsei University, Seoul 120-749, Korea e-mail: seoj@bubble.yonsei.ac.kr
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 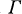be a curve in R2 defined by y = A(x). The Cauchy transform 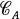on 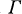is defined by the kernel

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 138 , June 1995 , pp. 19 - 32
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1995

Footnotes

This work was supported in part by GARC-KOSEF and NON-DIRECTED RESEARCH FUND, Korea Research Foundation, 1993.

References

[C] Calderón, A. P., Cauchy integrals on Lipschitz curves and related operators, Proc. Nat. Acad. Sci. USA, 74 (1977), 1324–1327.CrossRefGoogle ScholarPubMed
[CJS] Coifman, R. R., Jones, P., and Semmes, S., Two elementary proofs of the L-boundedness of Cauchy integrals on Lipschitz curves, J. Amer. Math. Soc, 2 (1989), 553–564.Google Scholar
[CMM] Coifman, R. R., McIntosh, A., Meyer, Y., L’intégrale de Cauchy definit un opérateur bornée sur L pour courbes lipschiziennes, Annals of Math., 116 (1982), 361–387.Google Scholar
[DJ] David, D. and Journé, J.-L., A boundedness criterion for generalized Calderón-Zygmund operators, Annals of Math., 120 (1984), 371–397.Google Scholar
[FJR] Fabes, E. B., Jodeit, M. Jr., and Riviere, N. M., Potential techniques for boundary value problems on (C1 -domains, Acta Math., 141 (1978), 165–186.Google Scholar
[KS] Kang, K. and Seo, J. K., L2 -boundedness of the Cauchy transform on smooth non-Lipschitz curves, Nagoya Math. J., 130 (1993), 123–147.Google Scholar
[M] Murai, T., A real variable method for the Cauchy transform, and analytic capacity, Lecture Note in Math., 1307, Springer-Verlag, New York, 1988.Google Scholar
[S] Stein, E., Singular Integrals and Differentiability Properties of Functions, Princeton Univ. Press Princeton, 1970.Google Scholar