Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Hu, Hui-Ya
and
Lan, Shi-Yi
2014.
Approximation of quasiconformal mappings by SG circle patterns.
Applicable Analysis,
Vol. 93,
Issue. 11,
p.
2360.
Lan, Shi-Yi
and
Dai, Dao-Qing
2016.
Discrete solutions of Dirichlet problems by circle patterns and finite volumes.
Applicable Analysis,
Vol. 95,
Issue. 4,
p.
902.
Lam, Wai Yeung
2018.
Discrete Minimal Surfaces: Critical Points of the Area Functional from Integrable Systems.
International Mathematics Research Notices,
Vol. 2018,
Issue. 6,
p.
1808.
Bobenko, Alexander
2025.
Spherical and hyperbolic orthogonal ring patterns: Integrability and variational principles.
Transactions of the American Mathematical Society,

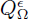 . By the Weierstrass representation of
. By the Weierstrass representation of 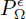 in ℂ with the combinatoric of
in ℂ with the combinatoric of 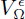 → ℝ
→ ℝ