Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Obata, Nobuaki
1989.
Some remarks on induced representations of infinite discrete groups.
Mathematische Annalen,
Vol. 284,
Issue. 1,
p.
91.
Obata, Nobuaki
1990.
Integral expression of some indecomposable characters of the infinite symmetric group in terms of irreducible representations.
Mathematische Annalen,
Vol. 287,
Issue. 1,
p.
369.
Hirai, Takeshi
1990.
Some aspects in the theory of representations of discrete groups, I.
Proceedings of the Japan Academy, Series A, Mathematical Sciences,
Vol. 66,
Issue. 10,
HIRAI, Takeshi
1990.
Some aspects in the theory of representations of discrete groups.
Japanese journal of mathematics. New series,
Vol. 16,
Issue. 2,
p.
197.
Albeverio, Sergio
and
Kosyak, Alexandre
2005.
Quasiregular representations of the infinite-dimensional Borel group.
Journal of Functional Analysis,
Vol. 218,
Issue. 2,
p.
445.

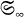 is the discrete group of all finite permutations of the set
is the discrete group of all finite permutations of the set 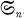 . Furthermore it is contained in infinite dimensional classical groups
. Furthermore it is contained in infinite dimensional classical groups 