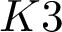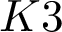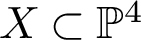Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Degtyarev, Alex
2023.
Conics on Kummer quartics.
Tohoku Mathematical Journal,
Vol. 75,
Issue. 3,
Degtyarev, Alex
2024.
Conics on Barth-Bauer octics.
Science China Mathematics,
Vol. 67,
Issue. 7,
p.
1507.