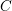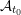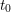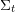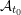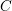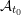1 Introduction and preliminaries
Cluster algebras with principal coefficients are important research objects in the theory of cluster algebras. The  $g$-vectors and the related
$g$-vectors and the related  $c$-vectors are introduced to describe cluster variables and coefficients in some sense. As shown in [Reference Nakanishi and Zelevinsky11],
$c$-vectors are introduced to describe cluster variables and coefficients in some sense. As shown in [Reference Nakanishi and Zelevinsky11],  $c$-vectors and
$c$-vectors and  $g$-vectors are closely related to each other, where the
$g$-vectors are closely related to each other, where the  $c$-vectors (respectively,
$c$-vectors (respectively,  $g$-vectors) are defined as the column vectors of C-matrices (respectively, G-matrices) of a cluster algebra with principal coefficients. In [Reference Fomin and Zelevinsky4], the authors conjectured as follows.
$g$-vectors) are defined as the column vectors of C-matrices (respectively, G-matrices) of a cluster algebra with principal coefficients. In [Reference Fomin and Zelevinsky4], the authors conjectured as follows.
Conjecture 1.1. [Reference Fomin and Zelevinsky4, Conjecture 4.7]
Let  ${\mathcal{A}}_{t_{0}}$ be the cluster algebra with principal coefficients at
${\mathcal{A}}_{t_{0}}$ be the cluster algebra with principal coefficients at  $\unicode[STIX]{x1D6F4}_{t_{0}}$ (or say at
$\unicode[STIX]{x1D6F4}_{t_{0}}$ (or say at  $t_{0}$), and let
$t_{0}$), and let  $\unicode[STIX]{x1D6F4}_{t}=(X_{t},\tilde{B}_{t})$ be a seed of
$\unicode[STIX]{x1D6F4}_{t}=(X_{t},\tilde{B}_{t})$ be a seed of  ${\mathcal{A}}_{t_{0}}$ obtained from
${\mathcal{A}}_{t_{0}}$ obtained from  $\unicode[STIX]{x1D6F4}_{t_{0}}$ by iterated mutations. Then
$\unicode[STIX]{x1D6F4}_{t_{0}}$ by iterated mutations. Then  $\unicode[STIX]{x1D6F4}_{t}$ is uniquely determined by
$\unicode[STIX]{x1D6F4}_{t}$ is uniquely determined by  $C_{t}$, where
$C_{t}$, where  $C_{t}$ is the lower part of
$C_{t}$ is the lower part of  $\tilde{B}_{t}=\left(\!\begin{smallmatrix}B_{t}\\ C_{t}\end{smallmatrix}\!\right)$.
$\tilde{B}_{t}=\left(\!\begin{smallmatrix}B_{t}\\ C_{t}\end{smallmatrix}\!\right)$.
Conjecture 1.1 is true in case  ${\mathcal{A}}_{t_{0}}$ is of finite type [Reference Reading and Speyer14], and in the skew-symmetric case [Reference Inoue, Iyama, Keller, Kuniba and Nakanishi7] using the methods in [Reference Plamondon12, Reference Plamondon13].
${\mathcal{A}}_{t_{0}}$ is of finite type [Reference Reading and Speyer14], and in the skew-symmetric case [Reference Inoue, Iyama, Keller, Kuniba and Nakanishi7] using the methods in [Reference Plamondon12, Reference Plamondon13].
In this paper, we give an affirmation of Conjecture 1.1 for any skew-symmetrizable cluster algebra  ${\mathcal{A}}_{t_{0}}$ with principal coefficients at
${\mathcal{A}}_{t_{0}}$ with principal coefficients at  $t_{0}$. The proof depends on the positivity of cluster variables and sign coherence of
$t_{0}$. The proof depends on the positivity of cluster variables and sign coherence of  $c$-vectors of
$c$-vectors of  ${\mathcal{A}}_{t_{0}}$. Note that the positivity of cluster variables for skew-symmetric cluster algebra was proved first by Lee and Schiffler [Reference Lee and Schiffler8] using the elementary method and the coherence of
${\mathcal{A}}_{t_{0}}$. Note that the positivity of cluster variables for skew-symmetric cluster algebra was proved first by Lee and Schiffler [Reference Lee and Schiffler8] using the elementary method and the coherence of  $c$-vectors for skew-symmetric cluster algebra was first proved by Derksen et al. [Reference Derksen, Weyman and Zelevinsky2] using the quivers with potentials and their representations. Recently both properties have been proved for skew-symmetrizable cluster algebra by Gross et al. [Reference Gross, Hacking, Keel and Kontsevich5] using the methods from algebraic geometry.
$c$-vectors for skew-symmetric cluster algebra was first proved by Derksen et al. [Reference Derksen, Weyman and Zelevinsky2] using the quivers with potentials and their representations. Recently both properties have been proved for skew-symmetrizable cluster algebra by Gross et al. [Reference Gross, Hacking, Keel and Kontsevich5] using the methods from algebraic geometry.
This paper is organized as follows. In this section, some basic definitions are introduced. In Section 2, we give the main result, that is, Theorem 2.5, which gives an affirmation of Conjecture 1.1 in the skew-symmetrizable case. In Section 3, we discuss the weak version of Conjecture 1.1 for acyclic totally sign-skew-symmetric cluster algebra using the method in Section 2.
Definition 1.2. Let  $A$ be an
$A$ be an  $(m+n)\times n$ integer matrix. The mutation of
$(m+n)\times n$ integer matrix. The mutation of  $A$ in direction
$A$ in direction  $k\in \{1,2,\ldots ,n\}$ is the
$k\in \{1,2,\ldots ,n\}$ is the  $(m+n)\times n$ matrix
$(m+n)\times n$ matrix  $\unicode[STIX]{x1D707}_{k}(A)=(a_{ij}^{\prime })$, satisfying
$\unicode[STIX]{x1D707}_{k}(A)=(a_{ij}^{\prime })$, satisfying
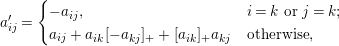 $$\begin{eqnarray}a_{ij}^{\prime }=\left\{\begin{array}{@{}ll@{}}-a_{ij},\quad & i=k~\text{or}~j=k;\\ a_{ij}+a_{ik}[-a_{kj}]_{+}+[a_{ik}]_{+}a_{kj}\quad & \text{otherwise},\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}a_{ij}^{\prime }=\left\{\begin{array}{@{}ll@{}}-a_{ij},\quad & i=k~\text{or}~j=k;\\ a_{ij}+a_{ik}[-a_{kj}]_{+}+[a_{ik}]_{+}a_{kj}\quad & \text{otherwise},\end{array}\right.\end{eqnarray}$$ where  $[a]_{+}=\max \{a,0\}$ for any
$[a]_{+}=\max \{a,0\}$ for any  $a\in \mathbb{R}$.
$a\in \mathbb{R}$.
Recall that an  $n\times n$ integer matrix
$n\times n$ integer matrix  $B=(b_{ij})$ is said to be sign-skew-symmetric if
$B=(b_{ij})$ is said to be sign-skew-symmetric if  $b_{ij}b_{ji}<0$ or
$b_{ij}b_{ji}<0$ or  $b_{ij}=b_{ji}=0$ for any
$b_{ij}=b_{ji}=0$ for any  $i,j=1,2,\ldots ,n$. A sign-skew-symmetric
$i,j=1,2,\ldots ,n$. A sign-skew-symmetric  $B$ is totally sign-skew-symmetric if any matrix
$B$ is totally sign-skew-symmetric if any matrix  $B^{\prime }$ obtained from
$B^{\prime }$ obtained from  $B$ by a sequence of mutations is sign-skew-symmetric.
$B$ by a sequence of mutations is sign-skew-symmetric.
An  $n\times n$ integer matrix
$n\times n$ integer matrix  $B=(b_{ij})$ is said to be skew-symmetrizable if there is a positive integer diagonal matrix
$B=(b_{ij})$ is said to be skew-symmetrizable if there is a positive integer diagonal matrix  $S$ such that
$S$ such that  $SB$ is skew-symmetric, where
$SB$ is skew-symmetric, where  $S$ is called the skew symmetrizer of
$S$ is called the skew symmetrizer of  $B$.
$B$.
It is well-known that skew symmetry and skew symmetrizability are invariant under mutation; thus skew-symmetrizable integer matrices are always totally sign-skew-symmetric.
For a sign-skew-symmetric matrix  $B$, we can encode the sign pattern of entries of
$B$, we can encode the sign pattern of entries of  $B$ by the directed graph
$B$ by the directed graph  $\unicode[STIX]{x1D6E4}(B)$ with the vertices
$\unicode[STIX]{x1D6E4}(B)$ with the vertices  $1,2,\ldots ,n$ and the directed edges
$1,2,\ldots ,n$ and the directed edges  $(i,j)$ for
$(i,j)$ for  $b_{ij}>0$. A sign-skew-symmetric matrix
$b_{ij}>0$. A sign-skew-symmetric matrix  $B$ is said to be acyclic if
$B$ is said to be acyclic if  $\unicode[STIX]{x1D6E4}(B)$ has no oriented cycles. As shown in [Reference Huang and Li6], an acyclic sign-skew-symmetric integer matrix
$\unicode[STIX]{x1D6E4}(B)$ has no oriented cycles. As shown in [Reference Huang and Li6], an acyclic sign-skew-symmetric integer matrix  $B$ is always totally sign-skew-symmetric.
$B$ is always totally sign-skew-symmetric.
Let  $\tilde{B}=\left(\!\begin{smallmatrix}B_{n\times n}\\ C_{m\times n}\end{smallmatrix}\!\right)=(\tilde{b}_{ij})$ be an
$\tilde{B}=\left(\!\begin{smallmatrix}B_{n\times n}\\ C_{m\times n}\end{smallmatrix}\!\right)=(\tilde{b}_{ij})$ be an  $(m+n)\times n$ integer matrix such that
$(m+n)\times n$ integer matrix such that  $B$ is totally sign-skew-symmetric.
$B$ is totally sign-skew-symmetric.  $\tilde{B}$ is said to be skew-symmetric, skew-symmetrizable, and (totally) sign-skew-symmetric, respectively if so is
$\tilde{B}$ is said to be skew-symmetric, skew-symmetrizable, and (totally) sign-skew-symmetric, respectively if so is  $B$.
$B$.
Definition 1.3. Let  ${\mathcal{F}}$ be the field of rational functions in
${\mathcal{F}}$ be the field of rational functions in  $m+n$ independent variables with coefficients
$m+n$ independent variables with coefficients  $\mathbb{Q}$. A (labeled) seed
$\mathbb{Q}$. A (labeled) seed  $\unicode[STIX]{x1D6F4}$ in
$\unicode[STIX]{x1D6F4}$ in  ${\mathcal{F}}$ is a pair
${\mathcal{F}}$ is a pair  $(X,\tilde{B})$, where
$(X,\tilde{B})$, where
(i)
 $\tilde{B}=\left(\!\begin{smallmatrix}B\\ C\end{smallmatrix}\!\right)$ is given as above, called an extended exchange matrix. The
$\tilde{B}=\left(\!\begin{smallmatrix}B\\ C\end{smallmatrix}\!\right)$ is given as above, called an extended exchange matrix. The $n\times n$ submatrix
$n\times n$ submatrix  $B$ is called an exchange matrix and the
$B$ is called an exchange matrix and the  $m\times n$ submatrix
$m\times n$ submatrix  $C$ is called a coefficient matrix.
$C$ is called a coefficient matrix.(ii)
 $X=(x_{1},\ldots ,x_{m+n})$ is an
$X=(x_{1},\ldots ,x_{m+n})$ is an  $(m+n)$-tuple, called an extended cluster with
$(m+n)$-tuple, called an extended cluster with  $x_{1},\ldots ,x_{m+n}$ forming a free generating set of
$x_{1},\ldots ,x_{m+n}$ forming a free generating set of  ${\mathcal{F}}$.
${\mathcal{F}}$.  $x_{1},\ldots ,x_{n}$ are called cluster variables and
$x_{1},\ldots ,x_{n}$ are called cluster variables and  $x_{n+1},\ldots ,x_{m+n}$ are called frozen variables. Sometimes we also write frozen variables as
$x_{n+1},\ldots ,x_{m+n}$ are called frozen variables. Sometimes we also write frozen variables as  $y_{1},\ldots ,y_{m}$ in this paper, that is,
$y_{1},\ldots ,y_{m}$ in this paper, that is,  $x_{n+i}=y_{i}$ for
$x_{n+i}=y_{i}$ for  $i=1,\ldots ,m$.
$i=1,\ldots ,m$.
Definition 1.4. Let  $k\in \{1,2,\ldots ,n\}$. The mutation of the seed
$k\in \{1,2,\ldots ,n\}$. The mutation of the seed  $\unicode[STIX]{x1D6F4}=(X,\tilde{B})$ in the direction
$\unicode[STIX]{x1D6F4}=(X,\tilde{B})$ in the direction  $k$ is the seed
$k$ is the seed  $\unicode[STIX]{x1D6F4}^{\prime }=(X^{\prime },\tilde{B}^{\prime })$ where
$\unicode[STIX]{x1D6F4}^{\prime }=(X^{\prime },\tilde{B}^{\prime })$ where  $\tilde{B}^{\prime }=\unicode[STIX]{x1D707}_{k}(\tilde{B})$ and
$\tilde{B}^{\prime }=\unicode[STIX]{x1D707}_{k}(\tilde{B})$ and  $X^{\prime }=(x_{1}^{\prime },\ldots ,x_{m+n}^{\prime })$ with
$X^{\prime }=(x_{1}^{\prime },\ldots ,x_{m+n}^{\prime })$ with  $x_{i}^{\prime }=x_{i}$ if
$x_{i}^{\prime }=x_{i}$ if  $i\neq k$ and
$i\neq k$ and
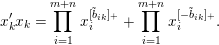 $$\begin{eqnarray}x_{k}^{\prime }x_{k}=\mathop{\prod }_{i=1}^{m+n}x_{i}^{[\tilde{b}_{ik}]_{+}}+\mathop{\prod }_{i=1}^{m+n}x_{i}^{[-\tilde{b}_{ik}]_{+}}.\end{eqnarray}$$
$$\begin{eqnarray}x_{k}^{\prime }x_{k}=\mathop{\prod }_{i=1}^{m+n}x_{i}^{[\tilde{b}_{ik}]_{+}}+\mathop{\prod }_{i=1}^{m+n}x_{i}^{[-\tilde{b}_{ik}]_{+}}.\end{eqnarray}$$ We write  $\unicode[STIX]{x1D6F4}^{\prime }=\unicode[STIX]{x1D707}_{k}(\unicode[STIX]{x1D6F4})$, where
$\unicode[STIX]{x1D6F4}^{\prime }=\unicode[STIX]{x1D707}_{k}(\unicode[STIX]{x1D6F4})$, where  $\unicode[STIX]{x1D707}_{k}$ is called the mutation map in
$\unicode[STIX]{x1D707}_{k}$ is called the mutation map in  $k$.
$k$.
It can be seen that the mutation map is always an involution, that is,  $\unicode[STIX]{x1D707}_{k}\unicode[STIX]{x1D707}_{k}(\unicode[STIX]{x1D6F4})=\unicode[STIX]{x1D6F4}$.
$\unicode[STIX]{x1D707}_{k}\unicode[STIX]{x1D707}_{k}(\unicode[STIX]{x1D6F4})=\unicode[STIX]{x1D6F4}$.
Definition 1.5. The cluster algebra  ${\mathcal{A}}(\unicode[STIX]{x1D6F4})$ is the
${\mathcal{A}}(\unicode[STIX]{x1D6F4})$ is the  $\mathbb{Z}[y_{1},\ldots ,y_{m}]$-subalgebra of
$\mathbb{Z}[y_{1},\ldots ,y_{m}]$-subalgebra of  ${\mathcal{F}}$ generated by all cluster variables obtained from the seed
${\mathcal{F}}$ generated by all cluster variables obtained from the seed  $\unicode[STIX]{x1D6F4}=(X,\tilde{B})$ by iterated mutations.
$\unicode[STIX]{x1D6F4}=(X,\tilde{B})$ by iterated mutations.  $\unicode[STIX]{x1D6F4}$ is called an initial seed of
$\unicode[STIX]{x1D6F4}$ is called an initial seed of  ${\mathcal{A}}(\unicode[STIX]{x1D6F4})$.
${\mathcal{A}}(\unicode[STIX]{x1D6F4})$.
A cluster algebra is said to be acyclic if it admits an acyclic exchange matrix.
Denote by  $I_{n}$ an
$I_{n}$ an  $n\times n$ identity matrix. If
$n\times n$ identity matrix. If  $\tilde{B}=\left(\!\begin{smallmatrix}B\\ I_{n}\end{smallmatrix}\!\right)$, then
$\tilde{B}=\left(\!\begin{smallmatrix}B\\ I_{n}\end{smallmatrix}\!\right)$, then  ${\mathcal{A}}(\unicode[STIX]{x1D6F4})$ is called the cluster algebra with principal coefficients at
${\mathcal{A}}(\unicode[STIX]{x1D6F4})$ is called the cluster algebra with principal coefficients at  $\unicode[STIX]{x1D6F4}$. In this case,
$\unicode[STIX]{x1D6F4}$. In this case,  $m=n$.
$m=n$.
Definition 1.6. [Reference Marsh9]
A cluster pattern  $M$ in
$M$ in  ${\mathcal{F}}$ is an assignment for each seed
${\mathcal{F}}$ is an assignment for each seed  $\unicode[STIX]{x1D6F4}_{t}$ to a vertex
$\unicode[STIX]{x1D6F4}_{t}$ to a vertex  $t$ of the
$t$ of the  $n$-regular tree
$n$-regular tree  $\mathbb{T}_{n}$, such that for any edge
$\mathbb{T}_{n}$, such that for any edge  $t~^{\text{}\underline{\quad k\quad }}~t^{\prime }$,
$t~^{\text{}\underline{\quad k\quad }}~t^{\prime }$,  $\unicode[STIX]{x1D6F4}_{t^{\prime }}=\unicode[STIX]{x1D707}_{k}(\unicode[STIX]{x1D6F4}_{t})$. The pair of
$\unicode[STIX]{x1D6F4}_{t^{\prime }}=\unicode[STIX]{x1D707}_{k}(\unicode[STIX]{x1D6F4}_{t})$. The pair of  $\unicode[STIX]{x1D6F4}_{t}$ is written as
$\unicode[STIX]{x1D6F4}_{t}$ is written as  $\unicode[STIX]{x1D6F4}_{t}=(X_{t},\tilde{B}_{t})$ with
$\unicode[STIX]{x1D6F4}_{t}=(X_{t},\tilde{B}_{t})$ with  $X_{t}=(x_{1;t},\ldots ,x_{m+n;t})$,
$X_{t}=(x_{1;t},\ldots ,x_{m+n;t})$,  $\tilde{B}_{t}=\left(\!\begin{smallmatrix}B_{t}\\ C_{t}\end{smallmatrix}\!\right)$, where
$\tilde{B}_{t}=\left(\!\begin{smallmatrix}B_{t}\\ C_{t}\end{smallmatrix}\!\right)$, where  $B_{t}=(b_{ij}^{t})$,
$B_{t}=(b_{ij}^{t})$,  $C_{t}=(c_{ij}^{t})$,
$C_{t}=(c_{ij}^{t})$,  $x_{n+i;t}=y_{i}$ for
$x_{n+i;t}=y_{i}$ for  $i=1,2,\ldots ,m$.
$i=1,2,\ldots ,m$.
Let  ${\mathcal{A}}_{t_{0}}$ be the cluster algebra with principal coefficients at
${\mathcal{A}}_{t_{0}}$ be the cluster algebra with principal coefficients at  $\unicode[STIX]{x1D6F4}_{t_{0}}$ (or say at
$\unicode[STIX]{x1D6F4}_{t_{0}}$ (or say at  $t_{0}$). The authors [Reference Fomin and Zelevinsky4] introduced a
$t_{0}$). The authors [Reference Fomin and Zelevinsky4] introduced a  $\mathbb{Z}^{n}$-grading of
$\mathbb{Z}^{n}$-grading of  $\mathbb{Z}[x_{1;t_{0}}^{\pm 1},\ldots ,x_{n;t_{0}}^{\pm 1},y_{1},\ldots ,y_{n}]$ as follows:
$\mathbb{Z}[x_{1;t_{0}}^{\pm 1},\ldots ,x_{n;t_{0}}^{\pm 1},y_{1},\ldots ,y_{n}]$ as follows:
 $$\begin{eqnarray}\deg (x_{i;t_{0}})=\boldsymbol{e}_{i},\qquad \deg (y_{j})=-\boldsymbol{b}_{j},\end{eqnarray}$$
$$\begin{eqnarray}\deg (x_{i;t_{0}})=\boldsymbol{e}_{i},\qquad \deg (y_{j})=-\boldsymbol{b}_{j},\end{eqnarray}$$ where  $\boldsymbol{e}_{i}$ is the
$\boldsymbol{e}_{i}$ is the  $i$th column vector of
$i$th column vector of  $I_{n}$ and
$I_{n}$ and  $\boldsymbol{b}_{j}$ is the
$\boldsymbol{b}_{j}$ is the  $j$th column vector of
$j$th column vector of  $B_{t_{0}}$,
$B_{t_{0}}$,  $i,j=1,2,\ldots ,n$. As shown in [Reference Fomin and Zelevinsky4], every cluster variable
$i,j=1,2,\ldots ,n$. As shown in [Reference Fomin and Zelevinsky4], every cluster variable  $x_{i;t}$ of
$x_{i;t}$ of  ${\mathcal{A}}_{t_{0}}$ is homogeneous with respect to this
${\mathcal{A}}_{t_{0}}$ is homogeneous with respect to this  $\mathbb{Z}^{n}$-grading. The
$\mathbb{Z}^{n}$-grading. The  $g$-vector of a cluster variable
$g$-vector of a cluster variable  $x_{i;t}$ is defined to be its degree with respect to the
$x_{i;t}$ is defined to be its degree with respect to the  $\mathbb{Z}^{n}$-grading and we write
$\mathbb{Z}^{n}$-grading and we write  $\deg (x_{i;t})=(g_{1i}^{t},g_{2i}^{t},\ldots ,g_{ni}^{t})^{\top }\in \mathbb{Z}^{n}$. Let
$\deg (x_{i;t})=(g_{1i}^{t},g_{2i}^{t},\ldots ,g_{ni}^{t})^{\top }\in \mathbb{Z}^{n}$. Let  $X_{t}$ be a cluster of
$X_{t}$ be a cluster of  ${\mathcal{A}}_{t_{0}}$. We call the matrix
${\mathcal{A}}_{t_{0}}$. We call the matrix  $G_{t}=(\deg (x_{1;t}),\ldots ,\deg (x_{n;t}))$ the G-matrix of the cluster
$G_{t}=(\deg (x_{1;t}),\ldots ,\deg (x_{n;t}))$ the G-matrix of the cluster  $X_{t}$. In addition,
$X_{t}$. In addition,  $C_{t}$ is called the C-matrix of
$C_{t}$ is called the C-matrix of  $\unicode[STIX]{x1D6F4}_{t}$, whose column vectors are called
$\unicode[STIX]{x1D6F4}_{t}$, whose column vectors are called  $c$-vectors (see [Reference Fomin and Zelevinsky4]).
$c$-vectors (see [Reference Fomin and Zelevinsky4]).
Proposition 1.7. Let  ${\mathcal{A}}_{t_{0}}$ be a cluster algebra with principal coefficients at
${\mathcal{A}}_{t_{0}}$ be a cluster algebra with principal coefficients at  $t_{0}$, let
$t_{0}$, let  $\unicode[STIX]{x1D6F4}_{t}$ be a seed of
$\unicode[STIX]{x1D6F4}_{t}$ be a seed of  ${\mathcal{A}}_{t_{0}}$, and let
${\mathcal{A}}_{t_{0}}$, and let  $\unicode[STIX]{x1D6F4}_{t^{\prime }}=\unicode[STIX]{x1D707}_{k}(\unicode[STIX]{x1D6F4})$. Then
$\unicode[STIX]{x1D6F4}_{t^{\prime }}=\unicode[STIX]{x1D707}_{k}(\unicode[STIX]{x1D6F4})$. Then
(i)
 $c_{ij}^{t^{\prime }}=\left\{\begin{array}{@{}ll@{}}-c_{ij}^{t},\quad & j=k;\\ c_{ij}^{t}+b_{ik}^{t}[-b_{kj}^{t}]_{+}+[c_{ik}^{t}]_{+}b_{kj}^{t}\quad & \text{otherwise}.\end{array}\right.$
$c_{ij}^{t^{\prime }}=\left\{\begin{array}{@{}ll@{}}-c_{ij}^{t},\quad & j=k;\\ c_{ij}^{t}+b_{ik}^{t}[-b_{kj}^{t}]_{+}+[c_{ik}^{t}]_{+}b_{kj}^{t}\quad & \text{otherwise}.\end{array}\right.$(ii) [Reference Fomin and Zelevinsky4, Proposition 6.6]
 $$\begin{eqnarray}g_{ij}^{t^{\prime }}=\left\{\begin{array}{@{}ll@{}}g_{ij}^{t},\quad & j\neq k;\\ -g_{ik}^{t}+\displaystyle \mathop{\sum }_{l=1}^{n}g_{il}^{t}[b_{lk}^{t}]_{+}-\displaystyle \mathop{\sum }_{l=1}^{n}-b_{il}^{t_{0}}[c_{lk}^{t}],\quad & j=k.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}g_{ij}^{t^{\prime }}=\left\{\begin{array}{@{}ll@{}}g_{ij}^{t},\quad & j\neq k;\\ -g_{ik}^{t}+\displaystyle \mathop{\sum }_{l=1}^{n}g_{il}^{t}[b_{lk}^{t}]_{+}-\displaystyle \mathop{\sum }_{l=1}^{n}-b_{il}^{t_{0}}[c_{lk}^{t}],\quad & j=k.\end{array}\right.\end{eqnarray}$$
Proof. (i) It can be obtained from equality (1).◻
Let  ${\mathcal{A}}_{t_{0}}$ be the cluster algebra with principal coefficients at
${\mathcal{A}}_{t_{0}}$ be the cluster algebra with principal coefficients at  $t_{0}$. Each cluster variable
$t_{0}$. Each cluster variable  $x_{i;t}$ can be expressed as a rational function
$x_{i;t}$ can be expressed as a rational function
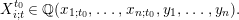 $$\begin{eqnarray}X_{i;t}^{t_{0}}\in \mathbb{Q}(x_{1;t_{0}},\ldots ,x_{n;t_{0}},y_{1},\ldots ,y_{n}).\end{eqnarray}$$
$$\begin{eqnarray}X_{i;t}^{t_{0}}\in \mathbb{Q}(x_{1;t_{0}},\ldots ,x_{n;t_{0}},y_{1},\ldots ,y_{n}).\end{eqnarray}$$ $X_{i;t}^{t_{0}}$ is called the
$X_{i;t}^{t_{0}}$ is called the  $X$-function of cluster variable
$X$-function of cluster variable  $x_{i;t}$.
$x_{i;t}$.
Definition 1.8. The  $F$-polynomial of
$F$-polynomial of  $x_{i;t}$ is defined by
$x_{i;t}$ is defined by
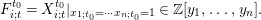 $$\begin{eqnarray}F_{i;t}^{t_{0}}=X_{i;t}^{t_{0}}|_{x_{1;t_{0}}=\cdots x_{n;t_{0}}=1}\in \mathbb{Z}[y_{1},\ldots ,y_{n}].\end{eqnarray}$$
$$\begin{eqnarray}F_{i;t}^{t_{0}}=X_{i;t}^{t_{0}}|_{x_{1;t_{0}}=\cdots x_{n;t_{0}}=1}\in \mathbb{Z}[y_{1},\ldots ,y_{n}].\end{eqnarray}$$ A vector  $\boldsymbol{c}\in \mathbb{Z}^{n}$ is said to be sign-coherent [Reference Fomin and Zelevinsky4] if any two nonzero entries of
$\boldsymbol{c}\in \mathbb{Z}^{n}$ is said to be sign-coherent [Reference Fomin and Zelevinsky4] if any two nonzero entries of  $\boldsymbol{c}$ have the same sign.
$\boldsymbol{c}$ have the same sign.
Proposition 1.9. [Reference Fomin and Zelevinsky4, Reference Gross, Hacking, Keel and Kontsevich5]
Let  ${\mathcal{A}}_{t_{0}}$ be a cluster algebra with principal coefficients at
${\mathcal{A}}_{t_{0}}$ be a cluster algebra with principal coefficients at  $t_{0}$, and let
$t_{0}$, and let  $x_{i;t}$ be a cluster variable of
$x_{i;t}$ be a cluster variable of  ${\mathcal{A}}_{t_{0}}$. Then
${\mathcal{A}}_{t_{0}}$. Then
(i)
 $x_{i;t}=(\prod _{j=1}^{n}x_{j;t_{0}}^{g_{ji}^{t}})F_{i;t}^{t_{0}}|_{{\mathcal{F}}}({\hat{y}}_{1;t_{0}},\ldots ,{\hat{y}}_{n;t_{0}})$, where
$x_{i;t}=(\prod _{j=1}^{n}x_{j;t_{0}}^{g_{ji}^{t}})F_{i;t}^{t_{0}}|_{{\mathcal{F}}}({\hat{y}}_{1;t_{0}},\ldots ,{\hat{y}}_{n;t_{0}})$, where  ${\hat{y}}_{k;t_{0}}=y_{k}\prod _{i=1}^{n}x_{i;t_{0}}^{b_{ik}^{t_{0}}}$ for
${\hat{y}}_{k;t_{0}}=y_{k}\prod _{i=1}^{n}x_{i;t_{0}}^{b_{ik}^{t_{0}}}$ for  $k\in \{1,2,\ldots ,n\}$.
$k\in \{1,2,\ldots ,n\}$.(ii) The following are equivalent:
(a) The column vectors of
 $C_{t}$ are sign-coherent.
$C_{t}$ are sign-coherent.(b) Each
 $F$-polynomial has constant term
$F$-polynomial has constant term  $1$.
$1$.(c) Each
 $F$-polynomial has a unique monomial of maximal degree, which has coefficient
$F$-polynomial has a unique monomial of maximal degree, which has coefficient  $1$ and is divisible by all other occurring monomials.
$1$ and is divisible by all other occurring monomials.
2 Affirmation of Conjecture 1.1 in the skew-symmetrizable case
In this section, we give an affirmation of Conjecture 1.1 (see Theorem 2.5) in the skew-symmetrizable case depending on the results in [Reference Gross, Hacking, Keel and Kontsevich5], that is, Theorem 2.1 and Proposition 2.2.
Theorem 2.1. (Positivity, [Reference Gross, Hacking, Keel and Kontsevich5])
Any cluster variable  $x_{i;t}$ can be expressed as a Laurent polynomial in
$x_{i;t}$ can be expressed as a Laurent polynomial in  $\mathbb{Z}_{{\geqslant}0}[y_{1},\ldots ,y_{m}][x_{1;t_{0}}^{\pm 1},\ldots ,x_{n;t_{0}}^{\pm 1}]$ in a skew-symmetrizable cluster algebra
$\mathbb{Z}_{{\geqslant}0}[y_{1},\ldots ,y_{m}][x_{1;t_{0}}^{\pm 1},\ldots ,x_{n;t_{0}}^{\pm 1}]$ in a skew-symmetrizable cluster algebra  ${\mathcal{A}}(\unicode[STIX]{x1D6F4}_{t_{0}})$ with initial seed
${\mathcal{A}}(\unicode[STIX]{x1D6F4}_{t_{0}})$ with initial seed  $\unicode[STIX]{x1D6F4}_{t_{0}}$.
$\unicode[STIX]{x1D6F4}_{t_{0}}$.
Proposition 2.2. [Reference Gross, Hacking, Keel and Kontsevich5]
Let  ${\mathcal{A}}_{t_{0}}$ be a skew-symmetrizable cluster algebra with principal coefficients at
${\mathcal{A}}_{t_{0}}$ be a skew-symmetrizable cluster algebra with principal coefficients at  $t_{0}$, and let
$t_{0}$, and let  $x_{i;t}$ be a cluster variable of
$x_{i;t}$ be a cluster variable of  ${\mathcal{A}}_{t_{0}}$. Then the column vectors of
${\mathcal{A}}_{t_{0}}$. Then the column vectors of  $C_{t}$ are sign-coherent.
$C_{t}$ are sign-coherent.
Proposition 2.3. [Reference Cao and Li1, Reference Nakanishi10, Reference Nakanishi and Zelevinsky11]
Let  ${\mathcal{A}}_{t_{0}}$ be a skew-symmetrizable cluster algebra with principal coefficients
${\mathcal{A}}_{t_{0}}$ be a skew-symmetrizable cluster algebra with principal coefficients  $t_{0}$ and with skew symmetrizer
$t_{0}$ and with skew symmetrizer  $S$, and let
$S$, and let  $\unicode[STIX]{x1D6F4}_{t}$ be a seed of
$\unicode[STIX]{x1D6F4}_{t}$ be a seed of  ${\mathcal{A}}_{t_{0}}$. Then
${\mathcal{A}}_{t_{0}}$. Then  $G_{t}B_{t}S^{-1}G_{t}^{\top }=B_{t_{0}}S^{-1}$ and
$G_{t}B_{t}S^{-1}G_{t}^{\top }=B_{t_{0}}S^{-1}$ and  $SC_{t}S^{-1}G_{t}^{\top }=I_{n}$ and
$SC_{t}S^{-1}G_{t}^{\top }=I_{n}$ and  $\det (G_{t})=\pm 1$.
$\det (G_{t})=\pm 1$.
Lemma 2.4. Let  ${\mathcal{A}}_{t_{0}}$ be a cluster algebra with principal coefficients at
${\mathcal{A}}_{t_{0}}$ be a cluster algebra with principal coefficients at  $t_{0}$, and let
$t_{0}$, and let  $\unicode[STIX]{x1D6F4}_{t}=(X_{t},\tilde{B}_{t})$ be a seed of
$\unicode[STIX]{x1D6F4}_{t}=(X_{t},\tilde{B}_{t})$ be a seed of  ${\mathcal{A}}_{t_{0}}$. If
${\mathcal{A}}_{t_{0}}$. If  $G_{t}=I_{n}$, then
$G_{t}=I_{n}$, then  $\unicode[STIX]{x1D6F4}_{t}=\unicode[STIX]{x1D6F4}_{t_{0}}$.
$\unicode[STIX]{x1D6F4}_{t}=\unicode[STIX]{x1D6F4}_{t_{0}}$.
Proof. By Proposition 2.3 and  $G_{t}=I_{n}=G_{t_{0}}$, we obtain
$G_{t}=I_{n}=G_{t_{0}}$, we obtain  $B_{t}=B_{t_{0}}$ and
$B_{t}=B_{t_{0}}$ and  $C_{t}=I_{n}$. So we can also view
$C_{t}=I_{n}$. So we can also view  ${\mathcal{A}}_{t_{0}}$ as a cluster algebra with principal coefficients at
${\mathcal{A}}_{t_{0}}$ as a cluster algebra with principal coefficients at  $t$. Let
$t$. Let  $\unicode[STIX]{x1D6F4}_{t_{1}}$ be a seed of
$\unicode[STIX]{x1D6F4}_{t_{1}}$ be a seed of  ${\mathcal{A}}_{t_{0}}$; the
${\mathcal{A}}_{t_{0}}$; the  $C$-matrix of
$C$-matrix of  $\unicode[STIX]{x1D6F4}_{t_{1}}$ is always the lower part of
$\unicode[STIX]{x1D6F4}_{t_{1}}$ is always the lower part of  $\tilde{B}_{t_{1}}$, no matter which seed (
$\tilde{B}_{t_{1}}$, no matter which seed ( $\unicode[STIX]{x1D6F4}_{t_{0}}$ or
$\unicode[STIX]{x1D6F4}_{t_{0}}$ or  $\unicode[STIX]{x1D6F4}_{t}$) is chosen as the initial seed. By Proposition 2.3 again, we know the
$\unicode[STIX]{x1D6F4}_{t}$) is chosen as the initial seed. By Proposition 2.3 again, we know the  $G$-matrices of
$G$-matrices of  $\unicode[STIX]{x1D6F4}_{t_{1}}$ with respect to
$\unicode[STIX]{x1D6F4}_{t_{1}}$ with respect to  $\unicode[STIX]{x1D6F4}_{t_{0}}$ and
$\unicode[STIX]{x1D6F4}_{t_{0}}$ and  $\unicode[STIX]{x1D6F4}_{t}$ are the same. By Proposition 1.9(i), we know
$\unicode[STIX]{x1D6F4}_{t}$ are the same. By Proposition 1.9(i), we know
 $$\begin{eqnarray}\displaystyle x_{i;t}=x_{i;t_{0}}F_{i;t}^{t_{0}}\left(y_{1}\mathop{\prod }_{l=1}^{n}x_{l;t_{0}}^{b_{l1}^{t_{0}}},\ldots ,y_{n}\mathop{\prod }_{l=1}^{n}x_{l;t_{0}}^{b_{ln}^{t_{0}}}\right), & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle x_{i;t}=x_{i;t_{0}}F_{i;t}^{t_{0}}\left(y_{1}\mathop{\prod }_{l=1}^{n}x_{l;t_{0}}^{b_{l1}^{t_{0}}},\ldots ,y_{n}\mathop{\prod }_{l=1}^{n}x_{l;t_{0}}^{b_{ln}^{t_{0}}}\right), & & \displaystyle\end{eqnarray}$$ by viewing  $\unicode[STIX]{x1D6F4}_{t_{0}}$ as an initial seed and
$\unicode[STIX]{x1D6F4}_{t_{0}}$ as an initial seed and
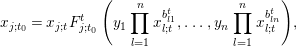 $$\begin{eqnarray}\displaystyle x_{j;t_{0}}=x_{j;t}F_{j;t_{0}}^{t}\left(y_{1}\mathop{\prod }_{l=1}^{n}x_{l;t}^{b_{l1}^{t}},\ldots ,y_{n}\mathop{\prod }_{l=1}^{n}x_{l;t}^{b_{ln}^{t}}\right)\!, & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle x_{j;t_{0}}=x_{j;t}F_{j;t_{0}}^{t}\left(y_{1}\mathop{\prod }_{l=1}^{n}x_{l;t}^{b_{l1}^{t}},\ldots ,y_{n}\mathop{\prod }_{l=1}^{n}x_{l;t}^{b_{ln}^{t}}\right)\!, & & \displaystyle\end{eqnarray}$$ by viewing  $\unicode[STIX]{x1D6F4}_{t}$ as an initial seed for
$\unicode[STIX]{x1D6F4}_{t}$ as an initial seed for  $i,j\in \{1,2,\ldots ,n\}$. Replacing
$i,j\in \{1,2,\ldots ,n\}$. Replacing  $x_{1;t_{0}},\ldots ,x_{n;t_{0}}$ in (2) with those in (3), we obtain that
$x_{1;t_{0}},\ldots ,x_{n;t_{0}}$ in (2) with those in (3), we obtain that
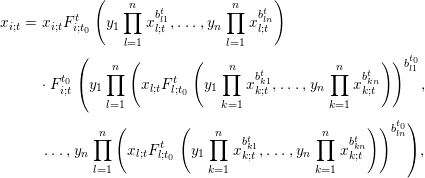 $$\begin{eqnarray}\displaystyle x_{i;t} & = & \displaystyle x_{i;t}F_{i;t_{0}}^{t}\left(y_{1}\mathop{\prod }_{l=1}^{n}x_{l;t}^{b_{l1}^{t}},\ldots ,y_{n}\mathop{\prod }_{l=1}^{n}x_{l;t}^{b_{ln}^{t}}\right)\nonumber\\ \displaystyle & & \displaystyle \cdot \,F_{i;t}^{t_{0}}\left(y_{1}\mathop{\prod }_{l=1}^{n}\left(x_{l;t}F_{l;t_{0}}^{t}\left(y_{1}\mathop{\prod }_{k=1}^{n}x_{k;t}^{b_{k1}^{t}},\ldots ,y_{n}\mathop{\prod }_{k=1}^{n}x_{k;t}^{b_{kn}^{t}}\right)\right)^{b_{l1}^{t_{0}}}\!,\right.\nonumber\\ \displaystyle & & \displaystyle \left.\ldots ,y_{n}\mathop{\prod }_{l=1}^{n}\left(x_{l;t}F_{l;t_{0}}^{t}\left(y_{1}\mathop{\prod }_{k=1}^{n}x_{k;t}^{b_{k1}^{t}},\ldots ,y_{n}\mathop{\prod }_{k=1}^{n}x_{k;t}^{b_{kn}^{t}}\right)\right)^{b_{ln}^{t_{0}}}\right)\!,\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle x_{i;t} & = & \displaystyle x_{i;t}F_{i;t_{0}}^{t}\left(y_{1}\mathop{\prod }_{l=1}^{n}x_{l;t}^{b_{l1}^{t}},\ldots ,y_{n}\mathop{\prod }_{l=1}^{n}x_{l;t}^{b_{ln}^{t}}\right)\nonumber\\ \displaystyle & & \displaystyle \cdot \,F_{i;t}^{t_{0}}\left(y_{1}\mathop{\prod }_{l=1}^{n}\left(x_{l;t}F_{l;t_{0}}^{t}\left(y_{1}\mathop{\prod }_{k=1}^{n}x_{k;t}^{b_{k1}^{t}},\ldots ,y_{n}\mathop{\prod }_{k=1}^{n}x_{k;t}^{b_{kn}^{t}}\right)\right)^{b_{l1}^{t_{0}}}\!,\right.\nonumber\\ \displaystyle & & \displaystyle \left.\ldots ,y_{n}\mathop{\prod }_{l=1}^{n}\left(x_{l;t}F_{l;t_{0}}^{t}\left(y_{1}\mathop{\prod }_{k=1}^{n}x_{k;t}^{b_{k1}^{t}},\ldots ,y_{n}\mathop{\prod }_{k=1}^{n}x_{k;t}^{b_{kn}^{t}}\right)\right)^{b_{ln}^{t_{0}}}\right)\!,\nonumber\end{eqnarray}$$which implies that
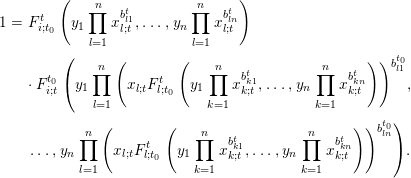 $$\begin{eqnarray}\displaystyle 1 & = & \displaystyle F_{i;t_{0}}^{t}\left(y_{1}\mathop{\prod }_{l=1}^{n}x_{l;t}^{b_{l1}^{t}},\ldots ,y_{n}\mathop{\prod }_{l=1}^{n}x_{l;t}^{b_{ln}^{t}}\right)\nonumber\\ \displaystyle & & \displaystyle \cdot \,F_{i;t}^{t_{0}}\left(y_{1}\mathop{\prod }_{l=1}^{n}\left(x_{l;t}F_{l;t_{0}}^{t}\left(y_{1}\mathop{\prod }_{k=1}^{n}x_{k;t}^{b_{k1}^{t}},\ldots ,y_{n}\mathop{\prod }_{k=1}^{n}x_{k;t}^{b_{kn}^{t}}\right)\right)^{b_{l1}^{t_{0}}}\!,\right.\nonumber\\ \displaystyle & & \displaystyle \left.\ldots ,y_{n}\mathop{\prod }_{l=1}^{n}\left(x_{l;t}F_{l;t_{0}}^{t}\left(y_{1}\mathop{\prod }_{k=1}^{n}x_{k;t}^{b_{k1}^{t}},\ldots ,y_{n}\mathop{\prod }_{k=1}^{n}x_{k;t}^{b_{kn}^{t}}\right)\right)^{b_{ln}^{t_{0}}}\right)\!.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 1 & = & \displaystyle F_{i;t_{0}}^{t}\left(y_{1}\mathop{\prod }_{l=1}^{n}x_{l;t}^{b_{l1}^{t}},\ldots ,y_{n}\mathop{\prod }_{l=1}^{n}x_{l;t}^{b_{ln}^{t}}\right)\nonumber\\ \displaystyle & & \displaystyle \cdot \,F_{i;t}^{t_{0}}\left(y_{1}\mathop{\prod }_{l=1}^{n}\left(x_{l;t}F_{l;t_{0}}^{t}\left(y_{1}\mathop{\prod }_{k=1}^{n}x_{k;t}^{b_{k1}^{t}},\ldots ,y_{n}\mathop{\prod }_{k=1}^{n}x_{k;t}^{b_{kn}^{t}}\right)\right)^{b_{l1}^{t_{0}}}\!,\right.\nonumber\\ \displaystyle & & \displaystyle \left.\ldots ,y_{n}\mathop{\prod }_{l=1}^{n}\left(x_{l;t}F_{l;t_{0}}^{t}\left(y_{1}\mathop{\prod }_{k=1}^{n}x_{k;t}^{b_{k1}^{t}},\ldots ,y_{n}\mathop{\prod }_{k=1}^{n}x_{k;t}^{b_{kn}^{t}}\right)\right)^{b_{ln}^{t_{0}}}\right)\!.\nonumber\end{eqnarray}$$ Take  $x_{1;t}=x_{2;t}=\cdots =x_{n;t}=1$ in the above equality; then we have
$x_{1;t}=x_{2;t}=\cdots =x_{n;t}=1$ in the above equality; then we have
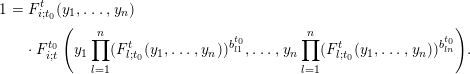 $$\begin{eqnarray}\displaystyle \quad 1 & = & \displaystyle F_{i;t_{0}}^{t}(y_{1},\ldots ,y_{n})\nonumber\\ \displaystyle & & \displaystyle \cdot \,F_{i;t}^{t_{0}}\left(y_{1}\mathop{\prod }_{l=1}^{n}(F_{l;t_{0}}^{t}(y_{1},\ldots ,y_{n}))^{b_{l1}^{t_{0}}},\ldots ,y_{n}\mathop{\prod }_{l=1}^{n}(F_{l;t_{0}}^{t}(y_{1},\ldots ,y_{n}))^{b_{ln}^{t_{0}}}\right)\!.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \quad 1 & = & \displaystyle F_{i;t_{0}}^{t}(y_{1},\ldots ,y_{n})\nonumber\\ \displaystyle & & \displaystyle \cdot \,F_{i;t}^{t_{0}}\left(y_{1}\mathop{\prod }_{l=1}^{n}(F_{l;t_{0}}^{t}(y_{1},\ldots ,y_{n}))^{b_{l1}^{t_{0}}},\ldots ,y_{n}\mathop{\prod }_{l=1}^{n}(F_{l;t_{0}}^{t}(y_{1},\ldots ,y_{n}))^{b_{ln}^{t_{0}}}\right)\!.\end{eqnarray}$$ By Theorem 2.1 and the definition of  $F$-polynomial, we have
$F$-polynomial, we have  $F_{j;t}^{t_{0}}$,
$F_{j;t}^{t_{0}}$,  $F_{j;t_{0}}^{t}\in \mathbb{Z}_{{\geqslant}0}[y_{1},\ldots ,y_{n}]$. Then we know each
$F_{j;t_{0}}^{t}\in \mathbb{Z}_{{\geqslant}0}[y_{1},\ldots ,y_{n}]$. Then we know each  $y_{j}\prod _{l=1}^{n}(F_{j;t_{0}}^{t}(y_{1},\ldots ,y_{n}))^{b_{lj}^{t_{0}}}$ has the form of
$y_{j}\prod _{l=1}^{n}(F_{j;t_{0}}^{t}(y_{1},\ldots ,y_{n}))^{b_{lj}^{t_{0}}}$ has the form of  $h_{j}/g_{j}$, where
$h_{j}/g_{j}$, where  $h_{j},g_{j}\in \mathbb{Z}_{{\geqslant}0}[y_{1},\ldots ,y_{n}]$,
$h_{j},g_{j}\in \mathbb{Z}_{{\geqslant}0}[y_{1},\ldots ,y_{n}]$,  $j=1,\ldots ,n$. We claim that
$j=1,\ldots ,n$. We claim that  $F_{i;t}^{t_{0}}(y_{1},\ldots ,y_{n})=1$. If
$F_{i;t}^{t_{0}}(y_{1},\ldots ,y_{n})=1$. If  $F_{i;t}^{t_{0}}(y_{1},\ldots ,y_{n})\neq 1$, then by Propositions 2.2 and 1.9(ii), we can assume
$F_{i;t}^{t_{0}}(y_{1},\ldots ,y_{n})\neq 1$, then by Propositions 2.2 and 1.9(ii), we can assume  $F_{i;t}^{t_{0}}=y_{1}^{k_{1i}}y_{2}^{k_{2i}}\cdots y_{n}^{k_{ni}}+u_{i}(y_{1},\ldots ,y_{n})+1$, where
$F_{i;t}^{t_{0}}=y_{1}^{k_{1i}}y_{2}^{k_{2i}}\cdots y_{n}^{k_{ni}}+u_{i}(y_{1},\ldots ,y_{n})+1$, where  $(k_{1i},\ldots ,k_{ni})\neq 0$,
$(k_{1i},\ldots ,k_{ni})\neq 0$,  $u_{i}\in \mathbb{Z}_{{\geqslant}0}[y_{1},\ldots ,y_{n}]$, and each monomial in
$u_{i}\in \mathbb{Z}_{{\geqslant}0}[y_{1},\ldots ,y_{n}]$, and each monomial in  $u_{i}$ is a factor of
$u_{i}$ is a factor of  $y_{1}^{k_{1i}}y_{2}^{k_{2i}}\cdots y_{n}^{k_{ni}}$. We assume
$y_{1}^{k_{1i}}y_{2}^{k_{2i}}\cdots y_{n}^{k_{ni}}$. We assume  $F_{i;t_{0}}^{t}=w_{i}(y_{1},\ldots ,y_{n})+1$, where
$F_{i;t_{0}}^{t}=w_{i}(y_{1},\ldots ,y_{n})+1$, where  $w_{i}\in \mathbb{Z}_{{\geqslant}0}[y_{1},\ldots ,y_{n}]$.
$w_{i}\in \mathbb{Z}_{{\geqslant}0}[y_{1},\ldots ,y_{n}]$.
Then equality (4) has the form
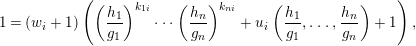 $$\begin{eqnarray}\displaystyle 1=(w_{i}+1)\left(\left(\frac{h_{1}}{g_{1}}\right)^{k_{1i}}\cdots \left(\frac{h_{n}}{g_{n}}\right)^{k_{ni}}+u_{i}\left(\frac{h_{1}}{g_{1}},\ldots ,\frac{h_{n}}{g_{n}}\right)+1\right), & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 1=(w_{i}+1)\left(\left(\frac{h_{1}}{g_{1}}\right)^{k_{1i}}\cdots \left(\frac{h_{n}}{g_{n}}\right)^{k_{ni}}+u_{i}\left(\frac{h_{1}}{g_{1}},\ldots ,\frac{h_{n}}{g_{n}}\right)+1\right), & & \displaystyle \nonumber\end{eqnarray}$$and thus
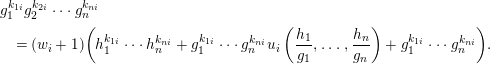 $$\begin{eqnarray}\displaystyle & \!\!\! & \displaystyle g_{1}^{k_{1i}}g_{2}^{k_{2i}}\cdots g_{n}^{k_{ni}}\nonumber\\ \displaystyle & \!\!\! & \displaystyle \quad =(w_{i}+1)\!\left(h_{1}^{k_{1i}}\cdots h_{n}^{k_{ni}}+g_{1}^{k_{1i}}\cdots g_{n}^{k_{ni}}u_{i}\left(\frac{h_{1}}{g_{1}},\ldots ,\frac{h_{n}}{g_{n}}\right)+g_{1}^{k_{1i}}\cdots g_{n}^{k_{ni}}\right)\!.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \!\!\! & \displaystyle g_{1}^{k_{1i}}g_{2}^{k_{2i}}\cdots g_{n}^{k_{ni}}\nonumber\\ \displaystyle & \!\!\! & \displaystyle \quad =(w_{i}+1)\!\left(h_{1}^{k_{1i}}\cdots h_{n}^{k_{ni}}+g_{1}^{k_{1i}}\cdots g_{n}^{k_{ni}}u_{i}\left(\frac{h_{1}}{g_{1}},\ldots ,\frac{h_{n}}{g_{n}}\right)+g_{1}^{k_{1i}}\cdots g_{n}^{k_{ni}}\right)\!.\nonumber\end{eqnarray}$$We obtain that
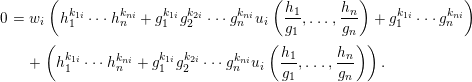 $$\begin{eqnarray}\displaystyle \quad 0 & = & \displaystyle w_{i}\left(h_{1}^{k_{1i}}\cdots h_{n}^{k_{ni}}+g_{1}^{k_{1i}}g_{2}^{k_{2i}}\cdots g_{n}^{k_{ni}}u_{i}\left(\frac{h_{1}}{g_{1}},\ldots ,\frac{h_{n}}{g_{n}}\right)+g_{1}^{k_{1i}}\cdots g_{n}^{k_{ni}}\right)\nonumber\\ \displaystyle & & \displaystyle +\left(h_{1}^{k_{1i}}\cdots h_{n}^{k_{ni}}+g_{1}^{k_{1i}}g_{2}^{k_{2i}}\cdots g_{n}^{k_{ni}}u_{i}\left(\frac{h_{1}}{g_{1}},\ldots ,\frac{h_{n}}{g_{n}}\right)\right).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \quad 0 & = & \displaystyle w_{i}\left(h_{1}^{k_{1i}}\cdots h_{n}^{k_{ni}}+g_{1}^{k_{1i}}g_{2}^{k_{2i}}\cdots g_{n}^{k_{ni}}u_{i}\left(\frac{h_{1}}{g_{1}},\ldots ,\frac{h_{n}}{g_{n}}\right)+g_{1}^{k_{1i}}\cdots g_{n}^{k_{ni}}\right)\nonumber\\ \displaystyle & & \displaystyle +\left(h_{1}^{k_{1i}}\cdots h_{n}^{k_{ni}}+g_{1}^{k_{1i}}g_{2}^{k_{2i}}\cdots g_{n}^{k_{ni}}u_{i}\left(\frac{h_{1}}{g_{1}},\ldots ,\frac{h_{n}}{g_{n}}\right)\right).\end{eqnarray}$$ Note that  $g_{1}^{k_{1i}}g_{2}^{k_{2i}}\cdots g_{n}^{k_{ni}}u_{i}(h_{1}/g_{1},\ldots ,h_{n}/g_{n})\in \mathbb{Z}_{{\geqslant}0}[y_{1},\ldots ,y_{n}]$, since each monomial occurring in
$g_{1}^{k_{1i}}g_{2}^{k_{2i}}\cdots g_{n}^{k_{ni}}u_{i}(h_{1}/g_{1},\ldots ,h_{n}/g_{n})\in \mathbb{Z}_{{\geqslant}0}[y_{1},\ldots ,y_{n}]$, since each monomial occurring in  $u_{i}(y_{1},\ldots ,y_{n})$ is a factor of
$u_{i}(y_{1},\ldots ,y_{n})$ is a factor of  $y_{1}^{k_{1i}}y_{2}^{k_{2i}}\cdots y_{n}^{k_{ni}}$. Then equality (5) is a contradiction, since each term in equality (5) is an element in
$y_{1}^{k_{1i}}y_{2}^{k_{2i}}\cdots y_{n}^{k_{ni}}$. Then equality (5) is a contradiction, since each term in equality (5) is an element in  $\mathbb{Z}_{{\geqslant}0}[y_{1},\ldots ,y_{n}]$ and
$\mathbb{Z}_{{\geqslant}0}[y_{1},\ldots ,y_{n}]$ and  $h_{1}^{k_{1i}}\cdots h_{n}^{k_{ni}}\neq 0$ by the fact that
$h_{1}^{k_{1i}}\cdots h_{n}^{k_{ni}}\neq 0$ by the fact that  $h_{j}\neq 0$,
$h_{j}\neq 0$,  $j=1,\ldots ,n$. Thus we must have
$j=1,\ldots ,n$. Thus we must have  $F_{i;t}^{t_{0}}(y_{1},\ldots ,y_{n})=1$, which implies
$F_{i;t}^{t_{0}}(y_{1},\ldots ,y_{n})=1$, which implies  $x_{i;t}=x_{i;t_{0}}$ by the equality (2). Then
$x_{i;t}=x_{i;t_{0}}$ by the equality (2). Then  $\unicode[STIX]{x1D6F4}_{t}=\unicode[STIX]{x1D6F4}_{t_{0}}$.◻
$\unicode[STIX]{x1D6F4}_{t}=\unicode[STIX]{x1D6F4}_{t_{0}}$.◻
Now, we obtain the main result as follows.
Theorem 2.5. Let  ${\mathcal{A}}_{t_{0}}$ be the cluster algebra with principal coefficients at
${\mathcal{A}}_{t_{0}}$ be the cluster algebra with principal coefficients at  $t_{0}$, and let
$t_{0}$, and let  $\unicode[STIX]{x1D6F4}_{t_{1}}$ and
$\unicode[STIX]{x1D6F4}_{t_{1}}$ and  $\unicode[STIX]{x1D6F4}_{t_{2}}$ be two seeds of
$\unicode[STIX]{x1D6F4}_{t_{2}}$ be two seeds of  ${\mathcal{A}}_{t_{0}}$. If
${\mathcal{A}}_{t_{0}}$. If  $C_{t_{1}}=C_{t_{2}}$, then
$C_{t_{1}}=C_{t_{2}}$, then  $\unicode[STIX]{x1D6F4}_{t_{1}}=\unicode[STIX]{x1D6F4}_{t_{2}}$.
$\unicode[STIX]{x1D6F4}_{t_{1}}=\unicode[STIX]{x1D6F4}_{t_{2}}$.
Proof. By Proposition 2.3 and due to  $C_{t_{1}}=C_{t_{2}}$, we have
$C_{t_{1}}=C_{t_{2}}$, we have  $B_{t_{1}}=B_{t_{2}}$ and
$B_{t_{1}}=B_{t_{2}}$ and  $G_{t_{1}}=G_{t_{2}}$. Since
$G_{t_{1}}=G_{t_{2}}$. Since  $\unicode[STIX]{x1D6F4}_{t_{0}}$ can be obtained from
$\unicode[STIX]{x1D6F4}_{t_{0}}$ can be obtained from  $\unicode[STIX]{x1D6F4}_{t_{1}}$ by a sequence of mutations, we write
$\unicode[STIX]{x1D6F4}_{t_{1}}$ by a sequence of mutations, we write  $\unicode[STIX]{x1D6F4}_{t_{0}}=\unicode[STIX]{x1D707}_{s_{k}}\cdots \unicode[STIX]{x1D707}_{s_{2}}\unicode[STIX]{x1D707}_{s_{1}}(\unicode[STIX]{x1D6F4}_{t_{1}})$. Let
$\unicode[STIX]{x1D6F4}_{t_{0}}=\unicode[STIX]{x1D707}_{s_{k}}\cdots \unicode[STIX]{x1D707}_{s_{2}}\unicode[STIX]{x1D707}_{s_{1}}(\unicode[STIX]{x1D6F4}_{t_{1}})$. Let  $\unicode[STIX]{x1D6F4}_{t}=\unicode[STIX]{x1D707}_{s_{k}}\cdots \unicode[STIX]{x1D707}_{s_{2}}\unicode[STIX]{x1D707}_{s_{1}}(\unicode[STIX]{x1D6F4}_{t_{2}})$. Since
$\unicode[STIX]{x1D6F4}_{t}=\unicode[STIX]{x1D707}_{s_{k}}\cdots \unicode[STIX]{x1D707}_{s_{2}}\unicode[STIX]{x1D707}_{s_{1}}(\unicode[STIX]{x1D6F4}_{t_{2}})$. Since  $(G_{t_{1}},C_{t_{1}},B_{t_{1}})=(G_{t_{2}},C_{t_{2}},B_{t_{2}})$, by Proposition 1.7, we know that
$(G_{t_{1}},C_{t_{1}},B_{t_{1}})=(G_{t_{2}},C_{t_{2}},B_{t_{2}})$, by Proposition 1.7, we know that  $(G_{t},C_{t},B_{t})=(G_{t_{0}},C_{t_{0}},B_{t_{0}})=(I_{n},I_{n},B_{t_{0}})$. By Lemma 2.4, we know
$(G_{t},C_{t},B_{t})=(G_{t_{0}},C_{t_{0}},B_{t_{0}})=(I_{n},I_{n},B_{t_{0}})$. By Lemma 2.4, we know  $\unicode[STIX]{x1D6F4}_{t}=\unicode[STIX]{x1D6F4}_{t_{0}}$ and thus
$\unicode[STIX]{x1D6F4}_{t}=\unicode[STIX]{x1D6F4}_{t_{0}}$ and thus  $\unicode[STIX]{x1D707}_{s_{1}}\unicode[STIX]{x1D707}_{s_{2}}\cdots \unicode[STIX]{x1D707}_{s_{k}}(\unicode[STIX]{x1D6F4}_{t})=\unicode[STIX]{x1D707}_{s_{1}}\unicode[STIX]{x1D707}_{s_{2}}\cdots \unicode[STIX]{x1D707}_{s_{k}}(\unicode[STIX]{x1D6F4}_{t_{0}})$, that is,
$\unicode[STIX]{x1D707}_{s_{1}}\unicode[STIX]{x1D707}_{s_{2}}\cdots \unicode[STIX]{x1D707}_{s_{k}}(\unicode[STIX]{x1D6F4}_{t})=\unicode[STIX]{x1D707}_{s_{1}}\unicode[STIX]{x1D707}_{s_{2}}\cdots \unicode[STIX]{x1D707}_{s_{k}}(\unicode[STIX]{x1D6F4}_{t_{0}})$, that is,  $\unicode[STIX]{x1D6F4}_{t_{2}}=\unicode[STIX]{x1D6F4}_{t_{1}}$.◻
$\unicode[STIX]{x1D6F4}_{t_{2}}=\unicode[STIX]{x1D6F4}_{t_{1}}$.◻
As readers can see, the proof of this result depends mainly on the positivity of cluster variables and sign coherence of  $c$-vectors of a cluster algebra. Positivity and sign coherence are two deep phenomena in cluster algebras. It is known in [Reference Nakanishi and Zelevinsky11] that sign coherence can relate to many other properties of cluster algebras. Also, we believe that positivity can be used to explain some other properties of cluster algebras. Through the method of the proof of Theorem 2.5, we attempt to provide an evidence for the essentiality of positivity and sign coherence.
$c$-vectors of a cluster algebra. Positivity and sign coherence are two deep phenomena in cluster algebras. It is known in [Reference Nakanishi and Zelevinsky11] that sign coherence can relate to many other properties of cluster algebras. Also, we believe that positivity can be used to explain some other properties of cluster algebras. Through the method of the proof of Theorem 2.5, we attempt to provide an evidence for the essentiality of positivity and sign coherence.
It was proved that  $\unicode[STIX]{x1D6F4}_{t}$ is uniquely determined by
$\unicode[STIX]{x1D6F4}_{t}$ is uniquely determined by  $G_{t}$ for a skew-symmetric matrix
$G_{t}$ for a skew-symmetric matrix  $B_{t_{0}}$ in [Reference Derksen, Weyman and Zelevinsky2]. By Proposition 2.3,
$B_{t_{0}}$ in [Reference Derksen, Weyman and Zelevinsky2]. By Proposition 2.3,  $C_{t_{1}}=C_{t_{2}}$ if and only if
$C_{t_{1}}=C_{t_{2}}$ if and only if  $G_{t_{1}}=G_{t_{2}}$. So, the result of Theorem 2.5 means that
$G_{t_{1}}=G_{t_{2}}$. So, the result of Theorem 2.5 means that  $\unicode[STIX]{x1D6F4}_{t}$ is uniquely determined by
$\unicode[STIX]{x1D6F4}_{t}$ is uniquely determined by  $G_{t}$, which gives a generalization of the result in [Reference Derksen, Weyman and Zelevinsky2] in the skew-symmetrizable case.
$G_{t}$, which gives a generalization of the result in [Reference Derksen, Weyman and Zelevinsky2] in the skew-symmetrizable case.
3 How to determine seed in the sign-skew-symmetric case
Finally, we discuss how to determine a seed using the  $C$-matrix or
$C$-matrix or  $G$-matrix in the sign-skew-symmetric case. The obtained result may be thought of as the weak version of Conjecture 1.1.
$G$-matrix in the sign-skew-symmetric case. The obtained result may be thought of as the weak version of Conjecture 1.1.
In this section, we always assume that  ${\mathcal{A}}_{t_{0}}$ is an acyclic sign-skew-symmetric cluster algebra with principal coefficients at
${\mathcal{A}}_{t_{0}}$ is an acyclic sign-skew-symmetric cluster algebra with principal coefficients at  $t_{0}$. Here, the “acyclic” condition is assumed since we need the following conclusion.
$t_{0}$. Here, the “acyclic” condition is assumed since we need the following conclusion.
Proposition 3.1. [Reference Huang and Li6, Theorems 7.11 and 7.13]
Let  ${\mathcal{A}}_{t_{0}}$ be an acyclic sign-skew-symmetric cluster algebra with principal coefficients at
${\mathcal{A}}_{t_{0}}$ be an acyclic sign-skew-symmetric cluster algebra with principal coefficients at  $t_{0}$. Then we have the following.
$t_{0}$. Then we have the following.
(i) Each cluster variable
 $x_{i;t}\in \mathbb{Z}_{{\geqslant}0}[y_{1},\ldots ,y_{m}][x_{1;t_{0}}^{\pm 1},\ldots ,x_{n;t_{0}}^{\pm 1}]$.
$x_{i;t}\in \mathbb{Z}_{{\geqslant}0}[y_{1},\ldots ,y_{m}][x_{1;t_{0}}^{\pm 1},\ldots ,x_{n;t_{0}}^{\pm 1}]$.(ii) Each
 $\boldsymbol{F}$-polynomial has constant term
$\boldsymbol{F}$-polynomial has constant term  $1$.
$1$.
Lemma 3.2. Let  ${\mathcal{A}}_{t_{0}}$ be an acyclic sign-skew-symmetric cluster algebra with principal coefficients at
${\mathcal{A}}_{t_{0}}$ be an acyclic sign-skew-symmetric cluster algebra with principal coefficients at  $t_{0}$. If
$t_{0}$. If  $\unicode[STIX]{x1D6F4}_{t}=(X_{t},\tilde{B}_{t})$ is a seed of
$\unicode[STIX]{x1D6F4}_{t}=(X_{t},\tilde{B}_{t})$ is a seed of  ${\mathcal{A}}_{t_{0}}$ satisfying
${\mathcal{A}}_{t_{0}}$ satisfying  $(G_{t},C_{t},B_{t})=(G_{t_{0}},C_{t_{0}},B_{t_{0}})$, then
$(G_{t},C_{t},B_{t})=(G_{t_{0}},C_{t_{0}},B_{t_{0}})$, then  $\unicode[STIX]{x1D6F4}_{t}=\unicode[STIX]{x1D6F4}_{t_{0}}$.
$\unicode[STIX]{x1D6F4}_{t}=\unicode[STIX]{x1D6F4}_{t_{0}}$.
Sketch of Proof.
Since  $C_{t}=C_{t_{0}}=I_{n}$ and
$C_{t}=C_{t_{0}}=I_{n}$ and  $G_{t}=G_{t_{0}}=I_{n}$,
$G_{t}=G_{t_{0}}=I_{n}$,  ${\mathcal{A}}_{t_{0}}$ can be also seen as a cluster algebra with principal coefficients at
${\mathcal{A}}_{t_{0}}$ can be also seen as a cluster algebra with principal coefficients at  $t$. Based on Proposition 3.1, we can use the same method with that of Lemma 2.4 so as to show
$t$. Based on Proposition 3.1, we can use the same method with that of Lemma 2.4 so as to show  $X_{t}=X_{t_{0}}$, which implies
$X_{t}=X_{t_{0}}$, which implies  $\unicode[STIX]{x1D6F4}_{t}=\unicode[STIX]{x1D6F4}_{t_{0}}$ since
$\unicode[STIX]{x1D6F4}_{t}=\unicode[STIX]{x1D6F4}_{t_{0}}$ since  $\tilde{B}_{t}=\tilde{B}_{t_{0}}$ is already known.◻
$\tilde{B}_{t}=\tilde{B}_{t_{0}}$ is already known.◻
Note that since we do not have the skew symmetrizer  $S$ in this case, Proposition 2.3 cannot be used here as in the proof of Lemma 2.4. This is the reason we need the condition
$S$ in this case, Proposition 2.3 cannot be used here as in the proof of Lemma 2.4. This is the reason we need the condition  $(G_{t},C_{t},B_{t})=(G_{t_{0}},C_{t_{0}},B_{t_{0}})$.
$(G_{t},C_{t},B_{t})=(G_{t_{0}},C_{t_{0}},B_{t_{0}})$.
Following Lemma 3.2, using the same method with the proof of Theorem 2.5, we have the following proposition.
Proposition 3.3. Let  ${\mathcal{A}}_{t_{0}}$ be an acyclic sign-skew-symmetric cluster algebra with principal coefficients at
${\mathcal{A}}_{t_{0}}$ be an acyclic sign-skew-symmetric cluster algebra with principal coefficients at  $t_{0}$. If
$t_{0}$. If  $\unicode[STIX]{x1D6F4}_{t_{1}}$ and
$\unicode[STIX]{x1D6F4}_{t_{1}}$ and  $\unicode[STIX]{x1D6F4}_{t_{1}}$ are two seeds of
$\unicode[STIX]{x1D6F4}_{t_{1}}$ are two seeds of  ${\mathcal{A}}_{t_{0}}$ with
${\mathcal{A}}_{t_{0}}$ with  $(G_{t_{1}},C_{t_{1}},B_{t_{1}})=(G_{t_{2}},C_{t_{2}},B_{t_{2}})$, then
$(G_{t_{1}},C_{t_{1}},B_{t_{1}})=(G_{t_{2}},C_{t_{2}},B_{t_{2}})$, then  $\unicode[STIX]{x1D6F4}_{t_{1}}=\unicode[STIX]{x1D6F4}_{t_{2}}$.
$\unicode[STIX]{x1D6F4}_{t_{1}}=\unicode[STIX]{x1D6F4}_{t_{2}}$.
Remark 3.4. When  $B_{t_{0}}$ is skew-symmetrizable, by Proposition 2.3, either
$B_{t_{0}}$ is skew-symmetrizable, by Proposition 2.3, either  $G_{t_{1}}=G_{t_{2}}$ or
$G_{t_{1}}=G_{t_{2}}$ or  $C_{t_{1}}=C_{t_{2}}$ implies
$C_{t_{1}}=C_{t_{2}}$ implies  $(G_{t_{1}},C_{t_{1}},B_{t_{1}})=(G_{t_{2}},C_{t_{2}},B_{t_{2}})$. So, Proposition 3.3 can be thought of as a weak version of Theorem 2.5 in the acyclic sign-skew-symmetric case.
$(G_{t_{1}},C_{t_{1}},B_{t_{1}})=(G_{t_{2}},C_{t_{2}},B_{t_{2}})$. So, Proposition 3.3 can be thought of as a weak version of Theorem 2.5 in the acyclic sign-skew-symmetric case.
Acknowledgments
The authors thank T. Nakanishi for his valuable comments on the earlier version of this paper. This project is supported by the National Natural Science Foundation of China (No. 11671350 and No. 11571173).