Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-13T02:34:51.551Z Has data issue: false hasContentIssue false
  • English
  • Français

DEGENERATING 0 IN TRIANGULATED CATEGORIES

Part of: Commutative algebra: Homological methods Homological methods

Published online by Cambridge University Press:  08 June 2020

MANUEL SAORÍN Open the ORCID record for MANUEL SAORÍN [Opens in a new window]  and
ALEXANDER ZIMMERMANN Open the ORCID record for ALEXANDER ZIMMERMANN [Opens in a new window]
MANUEL SAORÍN
Affiliation:
Departemento de Matemáticas, Universidad de Murcia, Aptdo. 4021, 30100 Espinardo, Murcia, Spain email msaorinc@um.es
ALEXANDER ZIMMERMANN
Affiliation:
Université de Picardie, Département de Mathématiques et LAMFA (UMR 7352 du CNRS), 33 rue St Leu, F-80039 Amiens Cedex 1, France email alexander.zimmermann@u-picardie.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

In previous work, based on the work of Zwara and Yoshino, we defined and studied degenerations of objects in triangulated categories analogous to the degeneration of modules. In triangulated categories 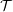${\mathcal{T}}$, it is surprising that the zero object may degenerate. We show that the triangulated subcategory of 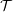${\mathcal{T}}$ generated by the objects that are degenerations of zero coincides with the triangulated subcategory of 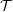${\mathcal{T}}$ consisting of the objects with a vanishing image in the Grothendieck group 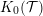$K_{0}({\mathcal{T}})$ of ${\mathcal{T}}$.

MSC classification

Primary: 16E35: Derived categories 13D09: Derived categories
Type
Article
Information
Nagoya Mathematical Journal , Volume 244 , December 2021 , pp. 158 - 167
Check for updates
Copyright
© 2020 Foundation Nagoya Mathematical Journal

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The first named author was supported by research projects of the Ministerio de Economía y Competitividad of Spain (MTM2016-77445-P) and the Fundación ‘Séneca’ of Murcia (19880/GERM/15), both with a part of FEDER funds.

References

Beilinson, A. A., Bernstein, J. and Deligne, P., Faisceaux Pervers, Astérisque 100 1 , Société Mathématique de France, 1982.Google Scholar
Bongartz, K., On degenerations and extensions of finite dimensional modules , Adv. Math. 121 (1996), 245–287.CrossRefGoogle Scholar
Eisele, F., The p-adic group ring of SL2(p f ) , J. Algebra 410 (2014), 421–459.CrossRefGoogle Scholar
Eisele, F., Blocks with a generalized quaternion defect group and three simple modules over a 2-adic ring , J. Algebra 456 (2016), 294–322.CrossRefGoogle Scholar
Gabriel, P., Finite Representation Type is Open, Proceedings of the International Conference on Representations of Algebras (Carleton University, Ottawa, Ontario, 1974), Paper No. 10, Carleton Mathematics Lecture Notes 9 , 23 Carleton University, Ottawa, Ontario, 1974.Google Scholar
Hiramatsu, N., Degenerations of graded Cohen–Macaulay modules , J. Comm. Algebra 7 (2015), 221–239.Google Scholar
Hiramatsu, N., On the stable hom relation and stable degenerations of Cohen–Macaulay modules , J. Pure Appl. Algebra 222 (2018), 2609–2625.CrossRefGoogle Scholar
Jensen, B. T., Su, X. and Zimmermann, A., Degeneration for derived categories , J. Pure Appl. Algebra 198 (2005), 281–295.CrossRefGoogle Scholar
Jensen, B. T., Su, X. and Zimmermann, A., Degeneration-like orders for triangulated categories , J. Algebra Appl. 4 (2005), 587–597.CrossRefGoogle Scholar
Keller, B., Yang, D. and Zhou, G., The Hall algebra of a spherical object , J. Lond. Math. Soc. 80 (2009), 771–784.CrossRefGoogle Scholar
Keller, B. and Scherotzke, S., Graded quiver varieties and derived categories , J. reine angew. Math. 713 (2016), 85–127.Google Scholar
Krause, H., Cohomological length functions , Nagoya Math. J. 223 (2016), 136–161.CrossRefGoogle Scholar
Neeman, A., Triangulated Categories, Princeton University Press, Princeton, MA, 2001.CrossRefGoogle Scholar
Riedtmann, C., Degenerations for representations of quivers with relations , Ann. Sci. Éc. Norm. Supér. 19 (1986), 275–301.CrossRefGoogle Scholar
Rose, D. E. V., A note on the Grothendieck group of an additive category , Vestnik Chelyabinskogo Gosudarstvennogo Universiteta. Matematika, Mekhanika, Informatika. NauchnyĭZhurnal 17(3) (2015), 135–139; Available at https://arxiv.org/pdf/1109.2040.pdf.Google Scholar
Saorín, M. and Zimmermann, A., An axiomatic approach for degenerations in triangulated categories , Appl. Categorical Struct. 24(4) (2016), 385–405.CrossRefGoogle Scholar
Saorín, M. and Zimmermann, A., Symmetry of the definition of degeneration in triangulated categories , Algebr. Represent. Theory 22 (2019), 801–836.Google Scholar
Thomason, R. W., The classification of triangulated subcategories , Compos. Math. 105 (1997), 1–27.CrossRefGoogle Scholar
Yoshino, Y., On degeneration of modules , J. Algebra 278 (2004), 217–226.CrossRefGoogle Scholar
Yoshino, Y., Stable degeneration of Cohen–Macaulay modules , J. Algebra 332 (2011), 500–521.CrossRefGoogle Scholar
Wang, Z., Triangle order ⩽𝛥 in singular categories , Algebr. Represent. Theory 19 (2016), 397–404.CrossRefGoogle Scholar
Zwara, G., A degeneration-like order for modules , Arch. Math. 71 (1998), 437–444.CrossRefGoogle Scholar
Zwara, G., Degenerations of finite dimensional modules are given by extensions , Compos. Math. 121 (2000), 205–218.CrossRefGoogle Scholar