1 Introduction
In this paper, we obtain a descent result for formal smoothness (and regularity). This single result (Theorem 1) has as particular cases a variety of (a priori unconnected) results in commutative algebra. Some of these particular cases greatly improve known important results (the descent of quasiexcellence by finite surjective morphisms [Reference Greco18], Kunz’s characterization of regular local rings in positive characteristic [Reference Kunz21, Reference Rodicio26], as well as its André–Radu relativization [Reference André2, Reference André3], and its analogue for complete intersections [Reference Blanco and Majadas15]); some other particular cases improve minor results of some papers [Reference Avramov7, Reference Avramov, Henriques and Şega10, Reference Avramov, Hochster, Iyengar and Yao11, Reference Dumitrescu16, Reference Dumitrescu17, Reference Takahashi and Yoshino32]; some others give already known theorems [Reference Rodicio27] or little results unexplored up to now (Corollary 25), but the point is that it is the same main result obtained to prove the descent of quasiexcellence the one that gives also those other results. Since this main result is rather technical, we confine ourselves in this introduction to discuss these applications in more detail.
1.1 Descent of quasiexcellence
The descent of quasiexcellence along flat local homomorphisms was studied in [Reference Greco18], where it was shown that quasiexcellence descends along finite flat local homomorphisms. We remove here this restriction, proving that this property descends along flat local homomorphisms of finite type. More precisely, Greco in [Reference Greco18] deduced this result from the following theorem: if
![]() $f:R\rightarrow S$
is a finite local homomorphism of noetherian local rings such that
$f:R\rightarrow S$
is a finite local homomorphism of noetherian local rings such that
![]() $\operatorname{Spec}(S)\rightarrow \operatorname{Spec}(R)$
is surjective, then quasiexcellence of
$\operatorname{Spec}(S)\rightarrow \operatorname{Spec}(R)$
is surjective, then quasiexcellence of
![]() $S$
implies quasiexcellence of
$S$
implies quasiexcellence of
![]() $R$
. He also obtained an example [Reference Greco18, Proposition 4.1] which shows that this last theorem cannot be extended to the case where
$R$
. He also obtained an example [Reference Greco18, Proposition 4.1] which shows that this last theorem cannot be extended to the case where
![]() $f$
is of finite type instead of finite, even when
$f$
is of finite type instead of finite, even when
![]() $R$
and
$R$
and
![]() $S$
are local domains of dimension 1 (the problem is concentrated in the local condition, that is, the geometric regularity of the formal fibers, since the J-2 property always descends and ascends by surjective morphisms of finite type [Reference Greco18, Corollary 2.4]). So the problem for finite type flat homomorphisms was left aside (however he was able to show that at least
$S$
are local domains of dimension 1 (the problem is concentrated in the local condition, that is, the geometric regularity of the formal fibers, since the J-2 property always descends and ascends by surjective morphisms of finite type [Reference Greco18, Corollary 2.4]). So the problem for finite type flat homomorphisms was left aside (however he was able to show that at least
![]() $R$
contains a nonempty principal open that is quasiexcellent), and he proceeded instead to consider proper surjective morphisms of schemes instead, a problem which was finally solved in [Reference Bellaccini14, Reference Ogoma24].
$R$
contains a nonempty principal open that is quasiexcellent), and he proceeded instead to consider proper surjective morphisms of schemes instead, a problem which was finally solved in [Reference Bellaccini14, Reference Ogoma24].
We reconsider here the problem for homomorphisms of finite type, and we will prove that it holds. Note first that if
![]() $\hat{R}$
and
$\hat{R}$
and
![]() ${\hat{S}}$
are the completions of
${\hat{S}}$
are the completions of
![]() $R$
and
$R$
and
![]() $S$
at their maximal ideals, the surjectivity of
$S$
at their maximal ideals, the surjectivity of
![]() $\operatorname{Spec}(S)\rightarrow \operatorname{Spec}(R)$
is equivalent to the surjectivity of
$\operatorname{Spec}(S)\rightarrow \operatorname{Spec}(R)$
is equivalent to the surjectivity of
![]() $\operatorname{Spec}({\hat{S}})\rightarrow \operatorname{Spec}(\hat{R})$
when
$\operatorname{Spec}({\hat{S}})\rightarrow \operatorname{Spec}(\hat{R})$
when
![]() $f$
is finite (but not necessarily when
$f$
is finite (but not necessarily when
![]() $f$
is of finite type). Then, a particular case of our main theorem gives the following theorem.
$f$
is of finite type). Then, a particular case of our main theorem gives the following theorem.
Theorem 7. Let
![]() $f:R\rightarrow S$
be a local homomorphism essentially of finite type (or more generally
$f:R\rightarrow S$
be a local homomorphism essentially of finite type (or more generally
![]() $S\otimes _{R}\hat{R}$
is noetherian) of noetherian local rings such that
$S\otimes _{R}\hat{R}$
is noetherian) of noetherian local rings such that
![]() $\operatorname{Spec}({\hat{S}})\rightarrow \operatorname{Spec}(\hat{R})$
is surjective. If
$\operatorname{Spec}({\hat{S}})\rightarrow \operatorname{Spec}(\hat{R})$
is surjective. If
![]() $S$
is quasiexcellent then
$S$
is quasiexcellent then
![]() $R$
is quasiexcellent. In particular, quasiexcellence descends along flat local homomorphisms (essentially) of finite type.
$R$
is quasiexcellent. In particular, quasiexcellence descends along flat local homomorphisms (essentially) of finite type.
1.2 Extension of Kunz’s theorem
In [Reference Kunz21], Kunz obtained the following result:
Theorem.
(Kunz) Let
![]() $A$
be a noetherian local ring containing a field of characteristic
$A$
be a noetherian local ring containing a field of characteristic
![]() $p>0$
, let
$p>0$
, let
![]() $\unicode[STIX]{x1D719}:A\rightarrow A,\unicode[STIX]{x1D719}(a)=a^{p}$
be the Frobenius homomorphism, and let
$\unicode[STIX]{x1D719}:A\rightarrow A,\unicode[STIX]{x1D719}(a)=a^{p}$
be the Frobenius homomorphism, and let
![]() $\text{}^{\unicode[STIX]{x1D719}}\!A$
be the ring
$\text{}^{\unicode[STIX]{x1D719}}\!A$
be the ring
![]() $A$
considered as
$A$
considered as
![]() $A$
-module via
$A$
-module via
![]() $\unicode[STIX]{x1D719}$
. Then
$\unicode[STIX]{x1D719}$
. Then
![]() $A$
is regular if and only if
$A$
is regular if and only if
![]() $\unicode[STIX]{x1D719}:A\rightarrow \text{}^{\unicode[STIX]{x1D719}}\!A$
is flat.
$\unicode[STIX]{x1D719}:A\rightarrow \text{}^{\unicode[STIX]{x1D719}}\!A$
is flat.
The relative case was obtained by Radu and André [Reference André2, Reference André3, Reference Radu25]:
Theorem.
(André, Radu) Let
![]() $\unicode[STIX]{x1D6FC}:A\rightarrow B$
be a homomorphism of noetherian rings containing a field of characteristic
$\unicode[STIX]{x1D6FC}:A\rightarrow B$
be a homomorphism of noetherian rings containing a field of characteristic
![]() $p>0$
. Then
$p>0$
. Then
![]() $\unicode[STIX]{x1D6FC}:A\rightarrow B$
is regular if and only if the relative Frobenius homomorphism
$\unicode[STIX]{x1D6FC}:A\rightarrow B$
is regular if and only if the relative Frobenius homomorphism
![]() $\unicode[STIX]{x1D719}_{B|A}:\text{}^{\unicode[STIX]{x1D719}}\!A\otimes _{A}B\rightarrow \text{}^{\unicode[STIX]{x1D719}}B$
is flat.
$\unicode[STIX]{x1D719}_{B|A}:\text{}^{\unicode[STIX]{x1D719}}\!A\otimes _{A}B\rightarrow \text{}^{\unicode[STIX]{x1D719}}B$
is flat.
This theorem contains Kunz’s result as a particular case: if
![]() $A$
is a noetherian local ring containing a field of characteristic
$A$
is a noetherian local ring containing a field of characteristic
![]() $p>0$
, then
$p>0$
, then
![]() $A$
contains a perfect field
$A$
contains a perfect field
![]() $F$
, and applying this theorem to the homomorphism
$F$
, and applying this theorem to the homomorphism
![]() $F\rightarrow A$
we recover Kunz’s theorem.
$F\rightarrow A$
we recover Kunz’s theorem.
The “if” part in the absolute Kunz’s theorem was extended in [Reference Avramov, Hochster, Iyengar and Yao11, Reference Avramov, Iyengar and Miller13, Reference Takahashi and Yoshino32], from the particular case of the Frobenius endomorphism to the more general case of a contracting endomorphism, that is, a homomorphism of noetherian local rings
![]() $f:(A,\mathfrak{m},k)\rightarrow (A,\mathfrak{m},k)$
such that there exists some
$f:(A,\mathfrak{m},k)\rightarrow (A,\mathfrak{m},k)$
such that there exists some
![]() $i>0$
with
$i>0$
with
![]() $f^{i}(\mathfrak{m})\subset \mathfrak{m}^{2}$
.
$f^{i}(\mathfrak{m})\subset \mathfrak{m}^{2}$
.
We show how our main result has also as a special case a relative version of these results for contracting homomorphisms, that is, we obtain a result (Theorem 13) generalizing at once both the relative result of André and Radu and the above extensions for contracting homomorphisms of the absolute result by Kunz.
1.3 Rodicio’s theorem
Theorem.
(Rodicio) Let
![]() $u:A\rightarrow B$
be a flat homomorphism of noetherian rings such that
$u:A\rightarrow B$
be a flat homomorphism of noetherian rings such that
![]() $B\otimes _{A}B$
is noetherian. If the flat (Tor) dimension of
$B\otimes _{A}B$
is noetherian. If the flat (Tor) dimension of
![]() $B$
over
$B$
over
![]() $B\otimes _{A}B$
is finite, then
$B\otimes _{A}B$
is finite, then
![]() $u$
is regular.
$u$
is regular.
This is the main result in [Reference Rodicio27]. Previous results on this topic were obtained by Auslander, Eilenberg, Harada, Hochschild, Nakayama, Rosenberg, Zelinsky and Rodicio himself among others. Our main result also has this theorem as a special case (Theorem 15). However, it should be noted that Rodicio’s proof is valid even when
![]() $B\otimes _{A}B$
is not noetherian.
$B\otimes _{A}B$
is not noetherian.
1.4 Decomposition of formal smoothness
Another particular case of our main result is the following one (Theorem 17). Let
![]() $A\xrightarrow[{}]{u}B\xrightarrow[{}]{v}C$
be local homomorphisms of noetherian local rings such that the flat dimension of
$A\xrightarrow[{}]{u}B\xrightarrow[{}]{v}C$
be local homomorphisms of noetherian local rings such that the flat dimension of
![]() $C$
over
$C$
over
![]() $B$
is finite; if
$B$
is finite; if
![]() $vu$
is formally smooth then
$vu$
is formally smooth then
![]() $u$
is formally smooth.
$u$
is formally smooth.
When
![]() $C$
is a flat
$C$
is a flat
![]() $B$
-module (i.e., the flat dimension is zero), the result is well known (it is an easy consequence of [Reference Grothendieck19,
$B$
-module (i.e., the flat dimension is zero), the result is well known (it is an easy consequence of [Reference Grothendieck19,
![]() $0_{IV}19.7.1$
,
$0_{IV}19.7.1$
,
![]() $0_{IV}22.5.8$
]). For finite flat dimension it follows from [Reference Avramov7, Theorem 4.7].
$0_{IV}22.5.8$
]). For finite flat dimension it follows from [Reference Avramov7, Theorem 4.7].
1.5 Other results
There are also a number of particular cases of our main result that, though important, they are well known and also easy to prove by using André–Quillen homology. We only point out a couple of them in order to stress the ubiquity of our main descent theorem (Examples 18).
In Section 2, we study similar questions for the complete intersection property instead of formal smoothness. For it, we need first some analogues of the main results of [Reference Avramov7] for finite complete intersection dimension instead of finite flat dimension (Theorem 20 – Remark 22). We now give a more reduced list of applications, since many of the ones given for formal smoothness are easy to translate to the complete intersection case.
We will use some facts of André–Quillen homology modules
![]() $H_{n}(A,B,M)$
. For convenience of the reader we list them in an Appendix with precise references.
$H_{n}(A,B,M)$
. For convenience of the reader we list them in an Appendix with precise references.
2 Formal smoothness
Theorem 1. Let
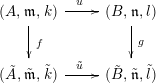
be a commutative square of local homomorphisms of noetherian local rings such that
-
(i)
 $\text{Tor}_{i}^{A}(\tilde{A},B)=0$
for all
$\text{Tor}_{i}^{A}(\tilde{A},B)=0$
for all
 $i>0$
.
$i>0$
. -
(ii) The homomorphism
 $H_{1}(A,B,\tilde{l})\rightarrow H_{1}(\tilde{A},\tilde{B},\tilde{l})$
vanishes.
$H_{1}(A,B,\tilde{l})\rightarrow H_{1}(\tilde{A},\tilde{B},\tilde{l})$
vanishes. -
(iii) If
 $\mathfrak{p}$
is the contraction in
$\mathfrak{p}$
is the contraction in
 $\tilde{A}\otimes _{A}B$
of the maximal ideal
$\tilde{A}\otimes _{A}B$
of the maximal ideal
 $\tilde{\mathfrak{n}}$
of
$\tilde{\mathfrak{n}}$
of
 $\tilde{B}$
, then
$\tilde{B}$
, then
 $(\tilde{A}\otimes _{A}B)_{\mathfrak{p}}$
is a noetherian ring.
$(\tilde{A}\otimes _{A}B)_{\mathfrak{p}}$
is a noetherian ring. -
(iv)
 $fd_{\tilde{A}\otimes _{A}B}(\tilde{B})<\infty$
.
$fd_{\tilde{A}\otimes _{A}B}(\tilde{B})<\infty$
.
Then
![]() $u:A\rightarrow B$
is formally smooth.
$u:A\rightarrow B$
is formally smooth.
Proof. The commutative diagram of ring homomorphisms
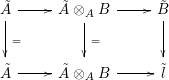
gives, taking Jacobi–Zariski sequences, a commutative square
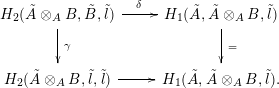
Associated to the ring homomorphisms
![]() $\tilde{A}\otimes _{A}B\rightarrow \tilde{B}\rightarrow \tilde{l}$
we have an exact sequence
$\tilde{A}\otimes _{A}B\rightarrow \tilde{B}\rightarrow \tilde{l}$
we have an exact sequence
where
![]() $\mathfrak{p}$
is the contraction in
$\mathfrak{p}$
is the contraction in
![]() $\tilde{A}\otimes _{A}B$
of the maximal ideal of
$\tilde{A}\otimes _{A}B$
of the maximal ideal of
![]() $\tilde{B}$
. Avramov’s result (Appendix 11) says that
$\tilde{B}$
. Avramov’s result (Appendix 11) says that
![]() $\unicode[STIX]{x1D6FD}$
is injective. Thus
$\unicode[STIX]{x1D6FD}$
is injective. Thus
![]() $\unicode[STIX]{x1D6FE}=0$
.
$\unicode[STIX]{x1D6FE}=0$
.
On the other hand, since
![]() $\text{Tor}_{i}^{A}(\tilde{A},B)=0$
for all
$\text{Tor}_{i}^{A}(\tilde{A},B)=0$
for all
![]() $i>0$
, the canonical homomorphism
$i>0$
, the canonical homomorphism
![]() $H_{1}(A,B,\tilde{l})\rightarrow H_{1}(\tilde{A},\tilde{A}\otimes _{A}B,\tilde{l})$
is an isomorphism, so the commutative triangle
$H_{1}(A,B,\tilde{l})\rightarrow H_{1}(\tilde{A},\tilde{A}\otimes _{A}B,\tilde{l})$
is an isomorphism, so the commutative triangle
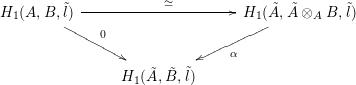
shows that
![]() $\unicode[STIX]{x1D6FC}=0$
. From the ring homomorphisms
$\unicode[STIX]{x1D6FC}=0$
. From the ring homomorphisms
![]() $\tilde{A}\rightarrow \tilde{A}\otimes _{A}B\rightarrow \tilde{B}$
, we obtain an exact sequence
$\tilde{A}\rightarrow \tilde{A}\otimes _{A}B\rightarrow \tilde{B}$
, we obtain an exact sequence
and then
![]() $\unicode[STIX]{x1D6FF}$
is surjective.
$\unicode[STIX]{x1D6FF}$
is surjective.
Thus, from the above commutative square we deduce that
![]() $H_{1} (\!\tilde{A}$
,
$H_{1} (\!\tilde{A}$
,
![]() $\tilde{A}\otimes _{A}B,\tilde{l}\!)=0$
, and so
$\tilde{A}\otimes _{A}B,\tilde{l}\!)=0$
, and so
![]() $H_{1}(A,B,\tilde{l})=0$
. This implies that
$H_{1}(A,B,\tilde{l})=0$
. This implies that
![]() $u:A\rightarrow B$
is formally smooth.◻
$u:A\rightarrow B$
is formally smooth.◻
Remark 2.
-
(i) In the particular case where
 $f$
and
$f$
and
 $g$
are the Frobenius endomorphisms, this result was proved in [Reference Dumitrescu17].
$g$
are the Frobenius endomorphisms, this result was proved in [Reference Dumitrescu17]. -
(ii) From the proof of Theorem 1, it is also clear that we can also weaken the condition
 $fd_{\tilde{A}\otimes _{A}B}(\tilde{B})<\infty$
as follows: there exists a local homomorphism of local noetherian rings
$fd_{\tilde{A}\otimes _{A}B}(\tilde{B})<\infty$
as follows: there exists a local homomorphism of local noetherian rings
 $\tilde{B}\rightarrow \tilde{C}$
such that the composition map
$\tilde{B}\rightarrow \tilde{C}$
such that the composition map
 $fd_{\tilde{A}\otimes _{A}B}(\tilde{C})<\infty$
.
$fd_{\tilde{A}\otimes _{A}B}(\tilde{C})<\infty$
.
In order to apply this result, it will be convenient to state some corollaries first:
Corollary 3. Let
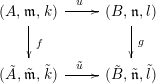
be a commutative square of local homomorphisms of noetherian local rings such that
-
(i)
 $\text{Tor}_{i}^{A}(\tilde{A},B)=0$
for all
$\text{Tor}_{i}^{A}(\tilde{A},B)=0$
for all
 $i>0$
.
$i>0$
. -
(ii) The homomorphism
 $H_{1}(A,B,\tilde{l})\rightarrow H_{1}(\tilde{A},\tilde{B},\tilde{l})$
is the zero map.
$H_{1}(A,B,\tilde{l})\rightarrow H_{1}(\tilde{A},\tilde{B},\tilde{l})$
is the zero map. -
(iii) The
 $\tilde{A}\otimes _{A}B$
-module
$\tilde{A}\otimes _{A}B$
-module
 $\tilde{B}$
is flat.
$\tilde{B}$
is flat.
Then
![]() $u:A\rightarrow B$
is formally smooth.
$u:A\rightarrow B$
is formally smooth.
Proof. Condition (iii) of Theorem 1 holds by faithfully flat descent. ◻
Corollary 4. Let

be a commutative square of homomorphisms of noetherian rings verifying
-
(i)
 $\text{Tor}_{i}^{A}(\tilde{A},B)=0$
for all
$\text{Tor}_{i}^{A}(\tilde{A},B)=0$
for all
 $i>0$
.
$i>0$
. -
(ii) For each
 $\mathfrak{q}\in \operatorname{Spec}(B)$
there exists
$\mathfrak{q}\in \operatorname{Spec}(B)$
there exists
 $\tilde{\mathfrak{q}}\in \operatorname{Spec}(\tilde{B})$
with
$\tilde{\mathfrak{q}}\in \operatorname{Spec}(\tilde{B})$
with
 $g^{-1}(\tilde{\mathfrak{q}})=\mathfrak{q}$
such that the map vanishes, where
$g^{-1}(\tilde{\mathfrak{q}})=\mathfrak{q}$
such that the map vanishes, where $$\begin{eqnarray}H_{1}(A,B,k(\tilde{\mathfrak{q}}))\rightarrow H_{1}(\tilde{A},\tilde{B},k(\tilde{\mathfrak{q}}))\end{eqnarray}$$
$$\begin{eqnarray}H_{1}(A,B,k(\tilde{\mathfrak{q}}))\rightarrow H_{1}(\tilde{A},\tilde{B},k(\tilde{\mathfrak{q}}))\end{eqnarray}$$
 $k(\tilde{\mathfrak{q}})$
is the residue field of
$k(\tilde{\mathfrak{q}})$
is the residue field of
 $\tilde{B}_{\tilde{\mathfrak{q}}}$
.
$\tilde{B}_{\tilde{\mathfrak{q}}}$
.
-
(iii) The
 $\tilde{A}\otimes _{A}B$
-module
$\tilde{A}\otimes _{A}B$
-module
 $\tilde{B}$
is flat.
$\tilde{B}$
is flat.
Then the homomorphism
![]() $u:A\rightarrow B$
is regular, that is, flat with geometrically regular fibers.
$u:A\rightarrow B$
is regular, that is, flat with geometrically regular fibers.
Proof. By [Reference Grothendieck19,
![]() $0_{IV}19.7.1$
, 22.5.8], we have to prove that the local homomorphism
$0_{IV}19.7.1$
, 22.5.8], we have to prove that the local homomorphism
![]() $A_{\mathfrak{p}}\rightarrow B_{\mathfrak{q}}$
is formally smooth for each
$A_{\mathfrak{p}}\rightarrow B_{\mathfrak{q}}$
is formally smooth for each
![]() $\mathfrak{q}\in \operatorname{Spec}(B)$
, where
$\mathfrak{q}\in \operatorname{Spec}(B)$
, where
![]() $\mathfrak{p}=u^{-1}(\mathfrak{q})$
. Let
$\mathfrak{p}=u^{-1}(\mathfrak{q})$
. Let
![]() $\tilde{\mathfrak{q}}\in \operatorname{Spec}(\tilde{B})$
such that
$\tilde{\mathfrak{q}}\in \operatorname{Spec}(\tilde{B})$
such that
![]() $g^{-1}(\tilde{\mathfrak{q}})=\mathfrak{q}$
as in condition (ii), and let
$g^{-1}(\tilde{\mathfrak{q}})=\mathfrak{q}$
as in condition (ii), and let
![]() $\tilde{\mathfrak{p}}=\tilde{u} ^{-1}(\tilde{\mathfrak{q}})$
. We have
$\tilde{\mathfrak{p}}=\tilde{u} ^{-1}(\tilde{\mathfrak{q}})$
. We have
-
(i)
 $\text{Tor}_{i}^{A_{\mathfrak{p}}}(\tilde{A}_{\tilde{\mathfrak{p}}},B_{\mathfrak{q}})=0$
for all
$\text{Tor}_{i}^{A_{\mathfrak{p}}}(\tilde{A}_{\tilde{\mathfrak{p}}},B_{\mathfrak{q}})=0$
for all
 $i>0$
.
$i>0$
. -
(ii) The homomorphism
is zero. $$\begin{eqnarray}\displaystyle H_{1}(A_{\mathfrak{p}},B_{\mathfrak{q}},k(\tilde{\mathfrak{q}})) & = & \displaystyle H_{1}(A,B,k(\tilde{\mathfrak{q}}))\rightarrow H_{1}(\tilde{A},\tilde{B},k(\tilde{\mathfrak{q}}))\nonumber\\ \displaystyle & = & \displaystyle H_{1}(\tilde{A}_{\tilde{\mathfrak{p}}},\tilde{B}_{\tilde{\mathfrak{q}}},k(\tilde{\mathfrak{q}}))\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle H_{1}(A_{\mathfrak{p}},B_{\mathfrak{q}},k(\tilde{\mathfrak{q}})) & = & \displaystyle H_{1}(A,B,k(\tilde{\mathfrak{q}}))\rightarrow H_{1}(\tilde{A},\tilde{B},k(\tilde{\mathfrak{q}}))\nonumber\\ \displaystyle & = & \displaystyle H_{1}(\tilde{A}_{\tilde{\mathfrak{p}}},\tilde{B}_{\tilde{\mathfrak{q}}},k(\tilde{\mathfrak{q}}))\nonumber\end{eqnarray}$$
-
(iii) The
 $\tilde{A}_{\tilde{\mathfrak{p}}}\otimes _{A_{\mathfrak{p}}}B_{\mathfrak{q}}$
-module
$\tilde{A}_{\tilde{\mathfrak{p}}}\otimes _{A_{\mathfrak{p}}}B_{\mathfrak{q}}$
-module
 $\tilde{B}_{\tilde{\mathfrak{q}}}$
is flat.
$\tilde{B}_{\tilde{\mathfrak{q}}}$
is flat.
Therefore we can apply Corollary 3 to the commutative square

and we obtain that
![]() $A_{\mathfrak{p}}\rightarrow B_{\mathfrak{q}}$
is formally smooth.◻
$A_{\mathfrak{p}}\rightarrow B_{\mathfrak{q}}$
is formally smooth.◻
In the applications, we will use frequently the following weaker version of the theorem:
Corollary 5. Let
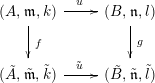
be a commutative square of local homomorphisms of noetherian local rings such that
-
(i)
 $\text{Tor}_{i}^{A}(\tilde{A},B)=0$
for all
$\text{Tor}_{i}^{A}(\tilde{A},B)=0$
for all
 $i>0$
.
$i>0$
. -
(ii) The homomorphism
 $\tilde{u} :\tilde{A}\rightarrow \tilde{B}$
is formally smooth.
$\tilde{u} :\tilde{A}\rightarrow \tilde{B}$
is formally smooth. -
(iii) The ring
 $\tilde{A}\otimes _{A}B$
is noetherian.
$\tilde{A}\otimes _{A}B$
is noetherian. -
(iv)
 $fd_{\tilde{A}\otimes _{A}B}(\tilde{B})<\infty$
.
$fd_{\tilde{A}\otimes _{A}B}(\tilde{B})<\infty$
.
Then
![]() $u:A\rightarrow B$
is formally smooth.
$u:A\rightarrow B$
is formally smooth.
Proof. Condition (ii) means
![]() $H_{1}(\tilde{A},\tilde{B},\tilde{l})=0$
.◻
$H_{1}(\tilde{A},\tilde{B},\tilde{l})=0$
.◻
Remark 6. Another particular case of Theorem 1, a little more general than Corollary 5, can be useful. It consists in substituting in Corollary 5 condition (ii) with:
(
![]() $\text{ii}^{\prime }$
) The square
$\text{ii}^{\prime }$
) The square
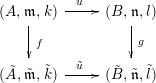
admits a factorization
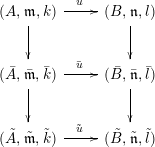
with
![]() $\bar{u}$
formally smooth.
$\bar{u}$
formally smooth.
2.1 Applications
2.1.1 Extension of Greco’s theorem
Let
![]() $u:R\rightarrow S$
be a local homomorphism of finite type of noetherian local rings. If
$u:R\rightarrow S$
be a local homomorphism of finite type of noetherian local rings. If
![]() $R$
is quasiexcellent then
$R$
is quasiexcellent then
![]() $S$
is quasiexcellent. We are concerned here with the reciprocal. In [Reference Greco18], Greco shows that if
$S$
is quasiexcellent. We are concerned here with the reciprocal. In [Reference Greco18], Greco shows that if
![]() $u$
is finite and
$u$
is finite and
![]() $\operatorname{Spec}(S)\rightarrow \operatorname{Spec}(R)$
is surjective then
$\operatorname{Spec}(S)\rightarrow \operatorname{Spec}(R)$
is surjective then
![]() $S$
quasiexcellent implies that
$S$
quasiexcellent implies that
![]() $R$
is quasiexcellent. He also proves that “
$R$
is quasiexcellent. He also proves that “
![]() $u$
finite” cannot be replaced by “
$u$
finite” cannot be replaced by “
![]() $u$
of finite type”, even when
$u$
of finite type”, even when
![]() $R$
and
$R$
and
![]() $S$
are local domains of dimension 1 [Reference Greco18, Proposition 4.1].
$S$
are local domains of dimension 1 [Reference Greco18, Proposition 4.1].
Instead of the surjectivity of
![]() $\operatorname{Spec}(S)\rightarrow \operatorname{Spec}(R)$
, we consider here the surjectivity of
$\operatorname{Spec}(S)\rightarrow \operatorname{Spec}(R)$
, we consider here the surjectivity of
![]() $\operatorname{Spec}({\hat{S}})\rightarrow \operatorname{Spec}(\hat{R})$
. When
$\operatorname{Spec}({\hat{S}})\rightarrow \operatorname{Spec}(\hat{R})$
. When
![]() $u$
is finite, both conditions are equivalent (since in this case
$u$
is finite, both conditions are equivalent (since in this case
![]() $\operatorname{Spec}({\hat{S}})\rightarrow \operatorname{Spec}(\hat{R})$
is obtained from
$\operatorname{Spec}({\hat{S}})\rightarrow \operatorname{Spec}(\hat{R})$
is obtained from
![]() $\operatorname{Spec}(S)\rightarrow \operatorname{Spec}(R)$
by base change and surjectivity of a morphism of schemas is a property stable by base change). However, for a homomorphism of finite type
$\operatorname{Spec}(S)\rightarrow \operatorname{Spec}(R)$
by base change and surjectivity of a morphism of schemas is a property stable by base change). However, for a homomorphism of finite type
![]() $u$
, the latter condition is in general strictly stronger. Then we can prove the following theorem.
$u$
, the latter condition is in general strictly stronger. Then we can prove the following theorem.
Theorem 7. Let
![]() $u:R\rightarrow S$
be a local homomorphism essentially of finite type of noetherian local rings such that
$u:R\rightarrow S$
be a local homomorphism essentially of finite type of noetherian local rings such that
![]() $\operatorname{Spec}({\hat{S}})\rightarrow \operatorname{Spec}(\hat{R})$
is surjective. If
$\operatorname{Spec}({\hat{S}})\rightarrow \operatorname{Spec}(\hat{R})$
is surjective. If
![]() $S$
is quasiexcellent then
$S$
is quasiexcellent then
![]() $R$
is quasiexcellent.
$R$
is quasiexcellent.
Proof. A noetherian local ring
![]() $A$
is quasiexcellent if and only if the homomorphism
$A$
is quasiexcellent if and only if the homomorphism
![]() $A\rightarrow \hat{A}$
is regular. So we apply Corollary 4 to the square
$A\rightarrow \hat{A}$
is regular. So we apply Corollary 4 to the square

and use for example [Reference Grothendieck20, 7.9.3.1] to see that
![]() $S\otimes _{R}\hat{R}\rightarrow {\hat{S}}$
is flat.◻
$S\otimes _{R}\hat{R}\rightarrow {\hat{S}}$
is flat.◻
Corollary 8. Let
![]() $R$
be a local ring and
$R$
be a local ring and
![]() $u:R\rightarrow S$
be a local flat homomorphism essentially of finite type. If
$u:R\rightarrow S$
be a local flat homomorphism essentially of finite type. If
![]() $S$
is quasiexcellent then
$S$
is quasiexcellent then
![]() $R$
is quasiexcellent.
$R$
is quasiexcellent.
Proof. Since
![]() $S$
is noetherian, so is
$S$
is noetherian, so is
![]() $R$
. The local homomorphism
$R$
. The local homomorphism
![]() $\hat{R}\rightarrow {\hat{S}}$
is flat by the local flatness criterion and so
$\hat{R}\rightarrow {\hat{S}}$
is flat by the local flatness criterion and so
![]() $\operatorname{Spec}({\hat{S}})\rightarrow \operatorname{Spec}(\hat{R})$
is surjective.◻
$\operatorname{Spec}({\hat{S}})\rightarrow \operatorname{Spec}(\hat{R})$
is surjective.◻
2.1.2 Extension of Kunz’s theorem
We will see now that another special case of Theorem 1 gives us a relative version of Kunz’s result for arbitrary contracting homomorphisms (Theorem 13; see the Introduction for comments). In order to guarantee that these homomorphisms satisfy the hypotheses of our theorem, first we will need to prove some facts. We start by noticing that [Reference Dumitrescu16, Lemma 1] holds also for contracting homomorphisms.
Lemma 9. Let
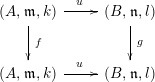
be a commutative square of local homomorphisms of noetherian local rings such that
![]() $f(\mathfrak{m})\subset \mathfrak{m}^{2}$
. If the homomorphism
$f(\mathfrak{m})\subset \mathfrak{m}^{2}$
. If the homomorphism
![]() $\unicode[STIX]{x1D714}:\text{}^{f}\!A\otimes _{A}B\rightarrow B$
,
$\unicode[STIX]{x1D714}:\text{}^{f}\!A\otimes _{A}B\rightarrow B$
,
![]() $\unicode[STIX]{x1D714}(a\otimes b)=u(a)g(b)$
, is flat then
$\unicode[STIX]{x1D714}(a\otimes b)=u(a)g(b)$
, is flat then
![]() $u$
is flat.
$u$
is flat.
Proof. By the local flatness criterion it suffices to show that
is flat for all
![]() $n\geqslant 1$
.
$n\geqslant 1$
.
We recall from the introduction that
![]() $\text{}^{f}\!A$
is the ring
$\text{}^{f}\!A$
is the ring
![]() $A$
considered as
$A$
considered as
![]() $A$
-module via
$A$
-module via
![]() $f:A\rightarrow A$
and similarly
$f:A\rightarrow A$
and similarly
![]() $\text{}^{g}\!B$
, etc. The homomorphism
$\text{}^{g}\!B$
, etc. The homomorphism
![]() $u=\text{}^{f}\!u$
factorizes as
$u=\text{}^{f}\!u$
factorizes as
and so
![]() $u_{n}=\text{}^{f}\!u_{n}=\text{}^{f}\!(A/\mathfrak{m}^{n})\otimes _{\text{}^{f}\!A}\text{}^{f}\!u$
factorizes as
$u_{n}=\text{}^{f}\!u_{n}=\text{}^{f}\!(A/\mathfrak{m}^{n})\otimes _{\text{}^{f}\!A}\text{}^{f}\!u$
factorizes as
where
![]() $\unicode[STIX]{x1D714}_{n}$
is defined in the obvious way as the natural map from the pushout of
$\unicode[STIX]{x1D714}_{n}$
is defined in the obvious way as the natural map from the pushout of
![]() $\text{}^{f}\!(A/\mathfrak{m}^{n})$
and
$\text{}^{f}\!(A/\mathfrak{m}^{n})$
and
![]() $B/\mathfrak{m}^{n}B$
over
$B/\mathfrak{m}^{n}B$
over
![]() $A/\mathfrak{m}^{n}$
.
$A/\mathfrak{m}^{n}$
.
But for
![]() $n\geqslant 2$
we have
$n\geqslant 2$
we have
(we have used that
![]() $f(\mathfrak{m})\subset \mathfrak{m}^{2}$
). The homomorphism
$f(\mathfrak{m})\subset \mathfrak{m}^{2}$
). The homomorphism
![]() $u_{1}$
is flat since
$u_{1}$
is flat since
![]() $A/\mathfrak{m}$
is a field. By induction, if
$A/\mathfrak{m}$
is a field. By induction, if
![]() $u_{n-1}$
is flat, then
$u_{n-1}$
is flat, then
![]() $\text{}^{f}\!(A/\mathfrak{m}^{n})\otimes _{A/\mathfrak{m}^{n}}u_{n}$
is flat and thus
$\text{}^{f}\!(A/\mathfrak{m}^{n})\otimes _{A/\mathfrak{m}^{n}}u_{n}$
is flat and thus
![]() $u_{n}=\unicode[STIX]{x1D714}_{n}\circ (\text{}^{f}\!(A/\mathfrak{m}^{n})\otimes _{A/\mathfrak{m}^{n}}u_{n})$
is flat, since
$u_{n}=\unicode[STIX]{x1D714}_{n}\circ (\text{}^{f}\!(A/\mathfrak{m}^{n})\otimes _{A/\mathfrak{m}^{n}}u_{n})$
is flat, since
![]() $\unicode[STIX]{x1D714}_{n}=\text{}^{f}\!(A/\mathfrak{m}^{n})\otimes _{\text{}^{f}\!A}\unicode[STIX]{x1D714}$
is flat for all
$\unicode[STIX]{x1D714}_{n}=\text{}^{f}\!(A/\mathfrak{m}^{n})\otimes _{\text{}^{f}\!A}\unicode[STIX]{x1D714}$
is flat for all
![]() $n\geqslant 1$
by base change.◻
$n\geqslant 1$
by base change.◻
Now a version of [Reference André1, 10.11] for contracting endomorphisms.
Lemma 10. Let
![]() $A$
be a noetherian ring,
$A$
be a noetherian ring,
![]() $I$
an ideal of
$I$
an ideal of
![]() $A$
,
$A$
,
![]() $M$
an
$M$
an
![]() $A$
-module of finite type,
$A$
-module of finite type,
![]() $f:A\rightarrow A$
a ring homomorphism such that
$f:A\rightarrow A$
a ring homomorphism such that
![]() $f(I)\subset I^{2}$
,
$f(I)\subset I^{2}$
,
![]() $g:M\rightarrow M$
an
$g:M\rightarrow M$
an
![]() $f$
-homomorphism (
$f$
-homomorphism (
![]() $g(am)=f(a)g(m)$
for
$g(am)=f(a)g(m)$
for
![]() $a\in A,m\in M$
), and
$a\in A,m\in M$
), and
![]() $n>0$
an integer. Then there exists an
$n>0$
an integer. Then there exists an
![]() $s>0$
such that the map induced by
$s>0$
such that the map induced by
![]() $f^{s}$
and
$f^{s}$
and
![]() $g^{s}$
(in all three variables)
$g^{s}$
(in all three variables)
is zero.
Proof. Let
be a resolution of
![]() $M$
with
$M$
with
![]() $F_{i}$
a projective
$F_{i}$
a projective
![]() $A$
-module of finite type for each
$A$
-module of finite type for each
![]() $i$
. Since
$i$
. Since
is the homology of the complex
we have
Applying
![]() $-\otimes _{A}A/I$
to the exact sequence
$-\otimes _{A}A/I$
to the exact sequence
we get
Thus
By the Artin–Rees lemma, there exists a positive integer
![]() $t$
such that
$t$
such that
![]() $\operatorname{Im}(d_{n})\cap I^{t}F_{n-1}\subset I\cdot \operatorname{Im}(d_{n})$
, so choosing
$\operatorname{Im}(d_{n})\cap I^{t}F_{n-1}\subset I\cdot \operatorname{Im}(d_{n})$
, so choosing
![]() $s$
such that
$s$
such that
![]() $f^{s}(I)\subset I^{t}$
we see that
$f^{s}(I)\subset I^{t}$
we see that
![]() $f^{s}$
and
$f^{s}$
and
![]() $g^{s}$
induce the zero map on
$g^{s}$
induce the zero map on
Proposition 11. Let
![]() $(A,\mathfrak{m},k)$
be a noetherian local ring and
$(A,\mathfrak{m},k)$
be a noetherian local ring and
![]() $f:A\rightarrow A$
a ring homomorphism such that
$f:A\rightarrow A$
a ring homomorphism such that
![]() $f(\mathfrak{m})\subset \mathfrak{m}^{2}$
. For each integer
$f(\mathfrak{m})\subset \mathfrak{m}^{2}$
. For each integer
![]() $n\geqslant 0$
there exists an integer
$n\geqslant 0$
there exists an integer
![]() $s>0$
such that
$s>0$
such that
![]() $f^{s}$
induces the zero map of functors
$f^{s}$
induces the zero map of functors
Proof. We mean that for any
![]() $k$
-module
$k$
-module
![]() $M$
, the map induced by
$M$
, the map induced by
![]() $f^{s}$
on the left two variables
$f^{s}$
on the left two variables
![]() $H_{n}(A,k,M)\rightarrow H_{n}(A,k,M)$
is zero, where in the left
$H_{n}(A,k,M)\rightarrow H_{n}(A,k,M)$
is zero, where in the left
![]() $H_{n}(A,k,M)$
,
$H_{n}(A,k,M)$
,
![]() $M$
is considered as
$M$
is considered as
![]() $k$
-module by restriction of scalars via the map
$k$
-module by restriction of scalars via the map
![]() $k\rightarrow k$
induced by
$k\rightarrow k$
induced by
![]() $f^{s}$
.
$f^{s}$
.
We have
![]() $H_{0}(A,k,k)=0$
, so we can assume
$H_{0}(A,k,k)=0$
, so we can assume
![]() $n>0$
. By Lemma 10, for
$n>0$
. By Lemma 10, for
![]() $i=1,\ldots ,n$
, we can choose integers
$i=1,\ldots ,n$
, we can choose integers
![]() $s_{i}$
such that
$s_{i}$
such that
![]() $f^{s_{i}}$
induces the zero map
$f^{s_{i}}$
induces the zero map
![]() $\text{Tor}_{i}^{A}(k,k)\rightarrow \text{Tor}_{i}^{A}(k,k)$
. We will use [Reference André1, 10.12] with
$\text{Tor}_{i}^{A}(k,k)\rightarrow \text{Tor}_{i}^{A}(k,k)$
. We will use [Reference André1, 10.12] with
![]() $A^{i}=A$
,
$A^{i}=A$
,
![]() $B^{i}=C^{i}=k$
for all
$B^{i}=C^{i}=k$
for all
![]() $i$
, and the homomorphisms
$i$
, and the homomorphisms
![]() $A^{i-1}\rightarrow A^{i}$
,
$A^{i-1}\rightarrow A^{i}$
,
![]() $B^{i-1}\rightarrow B^{i}$
,
$B^{i-1}\rightarrow B^{i}$
,
![]() $C^{i-1}\rightarrow C^{i}$
are the ones induced by
$C^{i-1}\rightarrow C^{i}$
are the ones induced by
![]() $f^{s_{i}}$
. We obtain that for
$f^{s_{i}}$
. We obtain that for
![]() $s\geqslant s_{1}+\cdots +s_{n}$
, the map
$s\geqslant s_{1}+\cdots +s_{n}$
, the map
![]() $H_{n}(A,k,-)\rightarrow H_{n}(A,k,-)$
induced by
$H_{n}(A,k,-)\rightarrow H_{n}(A,k,-)$
induced by
![]() $f^{s}$
is zero.◻
$f^{s}$
is zero.◻
Corollary 12. Let
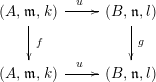
be a commutative square of local homomorphisms of noetherian local rings such that
![]() $f(\mathfrak{m})\subset \mathfrak{m}^{2}$
,
$f(\mathfrak{m})\subset \mathfrak{m}^{2}$
,
![]() $g(\mathfrak{n})\subset \mathfrak{n}^{2}$
. Then for each integer
$g(\mathfrak{n})\subset \mathfrak{n}^{2}$
. Then for each integer
![]() $n\geqslant 0$
there exists an integer
$n\geqslant 0$
there exists an integer
![]() $s>0$
such that
$s>0$
such that
![]() $(f^{s},g^{s})$
induces the zero homomorphism
$(f^{s},g^{s})$
induces the zero homomorphism
for any
![]() $l$
-module
$l$
-module
![]() $M$
.
$M$
.
Proof. We have a commutative diagram with exact rows
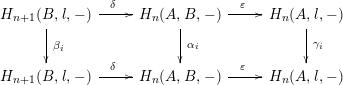
where the vertical maps are induced by
![]() $(f^{i},g^{i})$
. If
$(f^{i},g^{i})$
. If
![]() $\unicode[STIX]{x1D6FD}_{i}=0$
,
$\unicode[STIX]{x1D6FD}_{i}=0$
,
![]() $\unicode[STIX]{x1D6FE}_{i}=0$
, then
$\unicode[STIX]{x1D6FE}_{i}=0$
, then
![]() $\operatorname{Im}(\unicode[STIX]{x1D6FC}_{i})\subset \operatorname{Ker}(\unicode[STIX]{x1D700})=\operatorname{Im}(\unicode[STIX]{x1D6FF})$
and
$\operatorname{Im}(\unicode[STIX]{x1D6FC}_{i})\subset \operatorname{Ker}(\unicode[STIX]{x1D700})=\operatorname{Im}(\unicode[STIX]{x1D6FF})$
and
![]() $\operatorname{Im}(\unicode[STIX]{x1D6FF})\subset \operatorname{Ker}(\unicode[STIX]{x1D6FC}_{i})$
, so
$\operatorname{Im}(\unicode[STIX]{x1D6FF})\subset \operatorname{Ker}(\unicode[STIX]{x1D6FC}_{i})$
, so
![]() $\unicode[STIX]{x1D6FC}_{2i}=\unicode[STIX]{x1D6FC}_{i}^{2}=0$
. Therefore, taking
$\unicode[STIX]{x1D6FC}_{2i}=\unicode[STIX]{x1D6FC}_{i}^{2}=0$
. Therefore, taking
![]() $i$
sufficiently large, Proposition 11 gives the result.◻
$i$
sufficiently large, Proposition 11 gives the result.◻
Now, we can see that the required extension of Kunz’s theorem is also a particular case of our Theorem 1. Since we are placed in the local case, we do not need the flatness of
![]() $\unicode[STIX]{x1D714}$
, but only the flatness of its completion at the desired prime.
$\unicode[STIX]{x1D714}$
, but only the flatness of its completion at the desired prime.
Theorem 13. Let
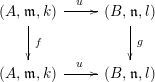
be a commutative square of local homomorphisms of noetherian local rings such that there exists some
![]() $i$
with
$i$
with
![]() $f^{i}(\mathfrak{m})\subset \mathfrak{m}^{2}$
,
$f^{i}(\mathfrak{m})\subset \mathfrak{m}^{2}$
,
![]() $g^{i}(\mathfrak{n})\subset \mathfrak{n}^{2}$
.
$g^{i}(\mathfrak{n})\subset \mathfrak{n}^{2}$
.
Denote by
![]() $\hat{A}$
and
$\hat{A}$
and
![]() $\hat{B}$
the completions of
$\hat{B}$
the completions of
![]() $A$
and
$A$
and
![]() $B$
at their maximal ideals. If there exists some
$B$
at their maximal ideals. If there exists some
![]() $j$
such that the homomorphism
$j$
such that the homomorphism
![]() $\hat{\unicode[STIX]{x1D714}}_{j}:\text{}^{f^{j}}\!\hat{A}\otimes _{\hat{A}}\hat{B}\rightarrow \text{}^{g^{j}}\!\hat{B}$
is flat, then
$\hat{\unicode[STIX]{x1D714}}_{j}:\text{}^{f^{j}}\!\hat{A}\otimes _{\hat{A}}\hat{B}\rightarrow \text{}^{g^{j}}\!\hat{B}$
is flat, then
![]() $u:A\rightarrow B$
is formally smooth.
$u:A\rightarrow B$
is formally smooth.
Proof. By [Reference Grothendieck19,
![]() $0_{IV}19.3.6$
], the homomorphism
$0_{IV}19.3.6$
], the homomorphism
![]() $u:A\rightarrow B$
is formally smooth if (and only if)
$u:A\rightarrow B$
is formally smooth if (and only if)
![]() $u:\hat{A}\rightarrow \hat{B}$
is. So we can assume that
$u:\hat{A}\rightarrow \hat{B}$
is. So we can assume that
![]() $\unicode[STIX]{x1D714}_{j}:\text{}^{f^{j}}\!A\otimes _{A}B\rightarrow \text{}^{g^{j}}\!B$
is flat. By Corollary 12 there exists an integer
$\unicode[STIX]{x1D714}_{j}:\text{}^{f^{j}}\!A\otimes _{A}B\rightarrow \text{}^{g^{j}}\!B$
is flat. By Corollary 12 there exists an integer
![]() $s$
such that
$s$
such that
![]() $(f^{is},g^{is})$
induces the zero homomorphism
$(f^{is},g^{is})$
induces the zero homomorphism
![]() $H_{1}(A,B,M)\rightarrow H_{1}(A,B,M)$
for any
$H_{1}(A,B,M)\rightarrow H_{1}(A,B,M)$
for any
![]() $l$
-module
$l$
-module
![]() $M$
. On the other hand, if
$M$
. On the other hand, if
![]() $\unicode[STIX]{x1D714}_{j}$
is flat, then
$\unicode[STIX]{x1D714}_{j}$
is flat, then
![]() $\unicode[STIX]{x1D714}_{2j}$
is also flat, since it coincides with the composition
$\unicode[STIX]{x1D714}_{2j}$
is also flat, since it coincides with the composition
of two flat homomorphisms. So, replacing
![]() $(f,g)$
by a suitable power
$(f,g)$
by a suitable power
![]() $(f^{t},g^{t})$
we can assume
$(f^{t},g^{t})$
we can assume
![]() $f(\mathfrak{m})\subset \mathfrak{m}^{2}$
,
$f(\mathfrak{m})\subset \mathfrak{m}^{2}$
,
![]() $\unicode[STIX]{x1D714}:\text{}^{f}\!A\otimes _{A}B\rightarrow ^{g}\!B$
flat, and the homomorphism
$\unicode[STIX]{x1D714}:\text{}^{f}\!A\otimes _{A}B\rightarrow ^{g}\!B$
flat, and the homomorphism
![]() $(f,g)$
induces the zero map
$(f,g)$
induces the zero map
![]() $H_{1}(A,B,M)\rightarrow H_{1}(A,B,M)$
.
$H_{1}(A,B,M)\rightarrow H_{1}(A,B,M)$
.
By Lemma 9,
![]() $u$
is flat. Then the result follows from Corollary 3.◻
$u$
is flat. Then the result follows from Corollary 3.◻
Remark 14. As a particular case of Theorem 13, we have obviously the original Kunz’s theorem (even for finite flat dimension instead of flatness if we use Theorem 1): let
![]() $A$
be a noetherian local ring containing a field of characteristic
$A$
be a noetherian local ring containing a field of characteristic
![]() $p>0$
, let
$p>0$
, let
![]() $\unicode[STIX]{x1D719}_{A}:A\rightarrow A$
be the Frobenius homomorphism. If
$\unicode[STIX]{x1D719}_{A}:A\rightarrow A$
be the Frobenius homomorphism. If
![]() $fd_{A}(\text{}^{\unicode[STIX]{x1D719}_{A}}A)<\infty$
then
$fd_{A}(\text{}^{\unicode[STIX]{x1D719}_{A}}A)<\infty$
then
![]() $A$
is regular. This result follows from Theorem 1 and Corollary 12 applied to the commutative square
$A$
is regular. This result follows from Theorem 1 and Corollary 12 applied to the commutative square

for some
![]() $s$
sufficiently large, where
$s$
sufficiently large, where
![]() $k$
is a perfect field contained in
$k$
is a perfect field contained in
![]() $A$
. When
$A$
. When
![]() $fd_{A}(\text{}^{\unicode[STIX]{x1D719}_{A}}A)=0$
this is Kunz’s result [Reference Kunz21], and in general it was obtained by Rodicio [Reference Rodicio26]. If we consider an arbitrary contracting endomorphism
$fd_{A}(\text{}^{\unicode[STIX]{x1D719}_{A}}A)=0$
this is Kunz’s result [Reference Kunz21], and in general it was obtained by Rodicio [Reference Rodicio26]. If we consider an arbitrary contracting endomorphism
![]() $\unicode[STIX]{x1D719}$
instead of
$\unicode[STIX]{x1D719}$
instead of
![]() $\unicode[STIX]{x1D719}_{A}$
, taking as
$\unicode[STIX]{x1D719}_{A}$
, taking as
![]() $k$
a perfect field contained in the subfield of elements of
$k$
a perfect field contained in the subfield of elements of
![]() $A$
fixed by
$A$
fixed by
![]() $\unicode[STIX]{x1D719}$
, we obtain a similar result, which by different methods was obtained previously in [Reference Avramov, Hochster, Iyengar and Yao11, Reference Takahashi and Yoshino32].
$\unicode[STIX]{x1D719}$
, we obtain a similar result, which by different methods was obtained previously in [Reference Avramov, Hochster, Iyengar and Yao11, Reference Takahashi and Yoshino32].
Finally, in the general setting, we may ask if our Theorem 1 gives also a relativization of [Reference Majadas22, Proposition 2]. That is, for a local homomorphism
![]() $f:A\rightarrow B$
, we ask if [Reference Majadas22, Proposition 2] is a consequence of our Theorem 1 applied to
$f:A\rightarrow B$
, we ask if [Reference Majadas22, Proposition 2] is a consequence of our Theorem 1 applied to
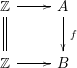
In general, the answer is no, since the homology vanishing hypothesis required for
![]() $f:A\rightarrow B$
in [Reference Majadas22] is weaker than ours. However, when
$f:A\rightarrow B$
in [Reference Majadas22] is weaker than ours. However, when
![]() $A$
contains a field, taking as before a perfect subfield
$A$
contains a field, taking as before a perfect subfield
![]() $k$
instead of
$k$
instead of
![]() $\mathbb{Z}$
, we can prove that the answer is affirmative.
$\mathbb{Z}$
, we can prove that the answer is affirmative.
2.1.3 Rodicio’s theorem
Theorem 15. Let
![]() $u:A\rightarrow B$
be a flat homomorphism of noetherian rings such that
$u:A\rightarrow B$
be a flat homomorphism of noetherian rings such that
![]() $B\otimes _{A}B$
is noetherian. If
$B\otimes _{A}B$
is noetherian. If
![]() $fd_{B\otimes _{A}B}(B)<\infty$
(via the multiplication map
$fd_{B\otimes _{A}B}(B)<\infty$
(via the multiplication map
![]() $\unicode[STIX]{x1D707}:B\otimes _{A}B\rightarrow B$
) then
$\unicode[STIX]{x1D707}:B\otimes _{A}B\rightarrow B$
) then
![]() $u$
is regular.
$u$
is regular.
Proof. This is the particular case
![]() $\tilde{A}=\tilde{B}=B$
. More precisely, apply Corollary 5 to the commutative square
$\tilde{A}=\tilde{B}=B$
. More precisely, apply Corollary 5 to the commutative square
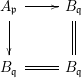
In this generality, this result was first proved by Rodicio [Reference Rodicio27] (even when
![]() $B\otimes _{A}B$
is not noetherian), and subsequently improved (in the noetherian case) by several authors.
$B\otimes _{A}B$
is not noetherian), and subsequently improved (in the noetherian case) by several authors.
Remark 16. We can see this result as a particular case of Corollary 5 also in a different way. Instead of the above square, we use

where
![]() $\mathfrak{c}=\unicode[STIX]{x1D707}^{-1}(\mathfrak{q})$
. We deduce that
$\mathfrak{c}=\unicode[STIX]{x1D707}^{-1}(\mathfrak{q})$
. We deduce that
![]() $(B\otimes _{A}B)_{\mathfrak{c}}$
is formally smooth over
$(B\otimes _{A}B)_{\mathfrak{c}}$
is formally smooth over
![]() $B_{\mathfrak{q}}$
and so
$B_{\mathfrak{q}}$
and so
that is,
![]() $ker(\unicode[STIX]{x1D707})$
is locally generated by a regular sequence.
$ker(\unicode[STIX]{x1D707})$
is locally generated by a regular sequence.
The value of this second approach is that it can be applied to an arbitrary noetherian supplemented
![]() $B$
-algebra
$B$
-algebra
![]() $S$
instead of
$S$
instead of
![]() $B\otimes _{A}B$
.
$B\otimes _{A}B$
.
2.1.4 Decomposition of formal smoothness
Theorem 17. Let
![]() $A\xrightarrow[{}]{u}B\xrightarrow[{}]{v}C$
be local homomorphisms of noetherian local rings such that
$A\xrightarrow[{}]{u}B\xrightarrow[{}]{v}C$
be local homomorphisms of noetherian local rings such that
![]() $vu$
is formally smooth and
$vu$
is formally smooth and
![]() $fd_{B}(C)<\infty$
. Then
$fd_{B}(C)<\infty$
. Then
![]() $u$
is formally smooth.
$u$
is formally smooth.
Proof. This result is Corollary 5 for
![]() $\tilde{A}=A$
,
$\tilde{A}=A$
,
![]() $\tilde{B}=C$
, that is, for the square
$\tilde{B}=C$
, that is, for the square

2.1.5 Other results
There are also other (well known) interesting particular cases of our main result, but they also can be easily proved with the help of André–Quillen homology. So we only state here a couple of them:
Examples 18. (a) 3. Let
![]() $(A,\mathfrak{m},k)\rightarrow (B,\mathfrak{n},l)$
be a flat local homomorphism of noetherian local rings. If
$(A,\mathfrak{m},k)\rightarrow (B,\mathfrak{n},l)$
be a flat local homomorphism of noetherian local rings. If
![]() $k\rightarrow B\otimes _{A}k$
is formally smooth then
$k\rightarrow B\otimes _{A}k$
is formally smooth then
![]() $A\rightarrow B$
is formally smooth.
$A\rightarrow B$
is formally smooth.
It follows from Corollary 5 applied to

This is part of [Reference Grothendieck19,
![]() $0_{IV}19.7.1$
] and it is also an immediate consequence of Appendix 4, 10.
$0_{IV}19.7.1$
] and it is also an immediate consequence of Appendix 4, 10.
(b) Let
![]() $u:(A,\mathfrak{m},k)\rightarrow (B,\mathfrak{n},l)$
be a flat local homomorphism of noetherian local rings. If
$u:(A,\mathfrak{m},k)\rightarrow (B,\mathfrak{n},l)$
be a flat local homomorphism of noetherian local rings. If
![]() $l|k$
is separable and
$l|k$
is separable and
![]() $B\otimes _{A}k$
is regular, then
$B\otimes _{A}k$
is regular, then
![]() $u$
is formally smooth.
$u$
is formally smooth.
We use the same square as in (a) with
![]() $B\otimes _{A}k$
replaced by
$B\otimes _{A}k$
replaced by
![]() $l$
. It can be also deduced from the Jacobi–Zariski exact sequence associated to
$l$
. It can be also deduced from the Jacobi–Zariski exact sequence associated to
![]() $k\rightarrow B\otimes _{A}k\rightarrow l$
and Appendix 4, 9, 10.
$k\rightarrow B\otimes _{A}k\rightarrow l$
and Appendix 4, 9, 10.
3 Complete intersection
We will now prove similar results for complete intersection instead of formal smoothness (Theorem 23 and its corollaries). We will need first a different version (Theorems 20 and 21) of two of the main theorems in [Reference Avramov7]. For convenience of the reader, we include here the details, though they are easy consequences of Avramov’s results.
Avramov [Reference Avramov5] introduces the virtual projective dimension (vpd) as follows (assuming for simplicity that the residue field of
![]() $A$
is infinite). An
$A$
is infinite). An
![]() $A$
-module
$A$
-module
![]() $M$
of finite type is said to be of finite virtual projective dimension if there exists a surjective homomorphism of noetherian local rings
$M$
of finite type is said to be of finite virtual projective dimension if there exists a surjective homomorphism of noetherian local rings
![]() $Q\rightarrow \hat{A}$
with kernel generated by a regular sequence such that the projective dimension
$Q\rightarrow \hat{A}$
with kernel generated by a regular sequence such that the projective dimension
![]() $\text{pd}_{Q}(\hat{A}\otimes _{A}M)$
is finite. The local ring
$\text{pd}_{Q}(\hat{A}\otimes _{A}M)$
is finite. The local ring
![]() $A$
is complete intersection if and only if any module of finite type has finite virtual projective dimension if and only if its residue field has finite virtual projective dimension.
$A$
is complete intersection if and only if any module of finite type has finite virtual projective dimension if and only if its residue field has finite virtual projective dimension.
Subsequently a modification of this concept, the complete intersection dimension, CI-dim, was introduced in [Reference Avramov, Gasharov and Peeva9]. In its definition, instead of the completion homomorphism
![]() $A\rightarrow \hat{A}$
, an arbitrary flat local homomorphism of noetherian local rings
$A\rightarrow \hat{A}$
, an arbitrary flat local homomorphism of noetherian local rings
![]() $A\rightarrow A^{\prime }$
is allowed. Complete intersection dimension shares many properties with virtual projective dimension, in particular the above equivalences. It also behaves well with respect to localization, but this advantage can also be considered as a symptom of some difficulties since complete intersection property of homomorphisms does not localize in general. If
$A\rightarrow A^{\prime }$
is allowed. Complete intersection dimension shares many properties with virtual projective dimension, in particular the above equivalences. It also behaves well with respect to localization, but this advantage can also be considered as a symptom of some difficulties since complete intersection property of homomorphisms does not localize in general. If
![]() $f:(A,\mathfrak{m},k)\rightarrow (B,\mathfrak{n},l)$
is a complete intersection homomorphism at the maximal ideal of
$f:(A,\mathfrak{m},k)\rightarrow (B,\mathfrak{n},l)$
is a complete intersection homomorphism at the maximal ideal of
![]() $B$
and
$B$
and
![]() $A$
has complete intersection formal fibers (for instance if
$A$
has complete intersection formal fibers (for instance if
![]() $A$
is a quotient of a local complete intersection ring; see [Reference Soto29]), then
$A$
is a quotient of a local complete intersection ring; see [Reference Soto29]), then
![]() $f$
is complete intersection at all primes [Reference Avramov7, Reference Marot23, Reference Tabaâ30, 5.12]. But in general, this property does not localize as we can see taking as
$f$
is complete intersection at all primes [Reference Avramov7, Reference Marot23, Reference Tabaâ30, 5.12]. But in general, this property does not localize as we can see taking as
![]() $f$
the completion homomorphism of a local ring whose formal fibers are not complete intersection.
$f$
the completion homomorphism of a local ring whose formal fibers are not complete intersection.
For this reason, we consider here a different definition of complete intersection dimension introduced in [Reference Soto29], cidim, that localizes when the ring has complete intersection formal fibers. Moreover, we have
![]() $\text{vpd}<\infty \Rightarrow \text{CI*\text{-}dim}<\infty \Rightarrow \text{cidim}<\infty \Rightarrow \text{CI\text{-}dim}<\infty$
, where CI*-dim is the upper complete intersection dimension introduced in [Reference Takahashi31].
$\text{vpd}<\infty \Rightarrow \text{CI*\text{-}dim}<\infty \Rightarrow \text{cidim}<\infty \Rightarrow \text{CI\text{-}dim}<\infty$
, where CI*-dim is the upper complete intersection dimension introduced in [Reference Takahashi31].
Let
![]() $f:(A,\mathfrak{m},k)\rightarrow (R,\mathfrak{n},l)$
be a local homomorphism of noetherian local rings. We say that
$f:(A,\mathfrak{m},k)\rightarrow (R,\mathfrak{n},l)$
be a local homomorphism of noetherian local rings. We say that
![]() $f$
is weakly regular if it is flat and the closed fiber
$f$
is weakly regular if it is flat and the closed fiber
![]() $R\otimes _{A}k$
is a regular ring. We say that
$R\otimes _{A}k$
is a regular ring. We say that
![]() $f$
is flat complete intersection at
$f$
is flat complete intersection at
![]() $\mathfrak{n}$
if it is flat and the closed fiber
$\mathfrak{n}$
if it is flat and the closed fiber
![]() $R\otimes _{A}k$
is a complete intersection ring. Since we will consider complete intersection homomorphisms always at the maximal ideal, we will simply say flat complete intersection homomorphism.
$R\otimes _{A}k$
is a complete intersection ring. Since we will consider complete intersection homomorphisms always at the maximal ideal, we will simply say flat complete intersection homomorphism.
If
![]() $f:(A,\mathfrak{m},k)\rightarrow (B,\mathfrak{n},l)$
is a local homomorphism of noetherian local rings, a regular factorization (resp. complete intersection factorization) of
$f:(A,\mathfrak{m},k)\rightarrow (B,\mathfrak{n},l)$
is a local homomorphism of noetherian local rings, a regular factorization (resp. complete intersection factorization) of
![]() $f$
is a factorization
$f$
is a factorization
![]() $A\xrightarrow[{}]{i}R\xrightarrow[{}]{p}B$
of
$A\xrightarrow[{}]{i}R\xrightarrow[{}]{p}B$
of
![]() $f$
where
$f$
where
![]() $R$
is a noetherian local ring,
$R$
is a noetherian local ring,
![]() $i$
is a weakly regular (resp. flat complete intersection) local homomorphism and
$i$
is a weakly regular (resp. flat complete intersection) local homomorphism and
![]() $p$
is surjective. If
$p$
is surjective. If
![]() $B$
is complete, a regular factorization (and so a complete intersection factorization) always exists [Reference Avramov, Foxby and Herzog8].
$B$
is complete, a regular factorization (and so a complete intersection factorization) always exists [Reference Avramov, Foxby and Herzog8].
We say that a finite module
![]() $M\neq 0$
over a noetherian local ring
$M\neq 0$
over a noetherian local ring
![]() $A$
has finite complete intersection dimension in the sense of [Reference Avramov, Gasharov and Peeva9] (resp. in the sense of [Reference Soto29]) and use the notation CI-dim
$A$
has finite complete intersection dimension in the sense of [Reference Avramov, Gasharov and Peeva9] (resp. in the sense of [Reference Soto29]) and use the notation CI-dim
![]() $(M)<\infty$
(resp. cidim
$(M)<\infty$
(resp. cidim
![]() $(M)<\infty$
) if there exist a flat (resp. flat complete intersection) local homomorphism of noetherian local rings
$(M)<\infty$
) if there exist a flat (resp. flat complete intersection) local homomorphism of noetherian local rings
![]() $A\rightarrow A^{\prime }$
, and a surjective homomorphism of noetherian local rings
$A\rightarrow A^{\prime }$
, and a surjective homomorphism of noetherian local rings
![]() $Q\rightarrow A^{\prime }$
with kernel generated by a regular sequence, such that
$Q\rightarrow A^{\prime }$
with kernel generated by a regular sequence, such that
![]() $pd_{Q}(M\otimes _{A}A^{\prime })<\infty$
, where
$pd_{Q}(M\otimes _{A}A^{\prime })<\infty$
, where
![]() $pd$
denotes projective dimension. For a local homomorphism of noetherian local rings
$pd$
denotes projective dimension. For a local homomorphism of noetherian local rings
![]() $f:A\rightarrow B$
we say that CI-dim
$f:A\rightarrow B$
we say that CI-dim
![]() $(f)<\infty$
(resp. cidim
$(f)<\infty$
(resp. cidim
![]() $(f)<\infty$
) if there exists a regular factorization (resp. complete intersection factorization)
$(f)<\infty$
) if there exists a regular factorization (resp. complete intersection factorization)
![]() $A\rightarrow R\rightarrow \hat{B}$
such that CI-dim
$A\rightarrow R\rightarrow \hat{B}$
such that CI-dim
![]() $_{R}(\hat{B})<\infty$
(resp. cidim
$_{R}(\hat{B})<\infty$
(resp. cidim
![]() $_{R}(\hat{B})<\infty$
).
$_{R}(\hat{B})<\infty$
).
If
![]() $fd_{A}(B)<\infty$
, then cidim
$fd_{A}(B)<\infty$
, then cidim
![]() $(f)<\infty$
(and so also CI-dim
$(f)<\infty$
(and so also CI-dim
![]() $(f)<\infty$
). Take a regular factorization
$(f)<\infty$
). Take a regular factorization
![]() $A\rightarrow R\rightarrow \hat{B}$
; from the change of rings spectral sequence
$A\rightarrow R\rightarrow \hat{B}$
; from the change of rings spectral sequence
we obtain
![]() $\text{Tor}_{n}^{R}(R\otimes _{A}k,\hat{B})=\text{Tor}_{n}^{A}(k,\hat{B})=0$
for all
$\text{Tor}_{n}^{R}(R\otimes _{A}k,\hat{B})=\text{Tor}_{n}^{A}(k,\hat{B})=0$
for all
![]() $n\gg 0$
, and then from the spectral sequence
$n\gg 0$
, and then from the spectral sequence
we deduce
![]() $\text{Tor}_{n}^{R}(\hat{B},l)=0$
for all
$\text{Tor}_{n}^{R}(\hat{B},l)=0$
for all
![]() $n\gg 0$
since
$n\gg 0$
since
![]() $R\otimes _{A}k$
is regular. That is,
$R\otimes _{A}k$
is regular. That is,
![]() $pd_{R}(\hat{B})=fd_{R}(\hat{B})<\infty$
. This immediately implies cidim
$pd_{R}(\hat{B})=fd_{R}(\hat{B})<\infty$
. This immediately implies cidim
![]() $(f)<\infty$
.
$(f)<\infty$
.
However, it is clear that cidim
![]() $(f)<\infty$
is far from implying
$(f)<\infty$
is far from implying
![]() $fd_{A}(B)<\infty$
(take as
$fd_{A}(B)<\infty$
(take as
![]() $A$
a complete intersection local ring and
$A$
a complete intersection local ring and
![]() $B$
its residue field).
$B$
its residue field).
We will need also the following lemma.
Lemma 19. (Essentially [Reference Avramov7, Lemma 1.7])
Let
![]() $(A,k)\xrightarrow[{}]{i}(R,l)\rightarrow (D,E)$
be local homomorphisms of noetherian local rings such that
$(A,k)\xrightarrow[{}]{i}(R,l)\rightarrow (D,E)$
be local homomorphisms of noetherian local rings such that
![]() $i$
is flat complete intersection. Then the canonical map
$i$
is flat complete intersection. Then the canonical map
![]() $H_{n}(A,D,E)\rightarrow H_{n}(R,D,E)$
is an isomorphism for all
$H_{n}(A,D,E)\rightarrow H_{n}(R,D,E)$
is an isomorphism for all
![]() $n\geqslant 3$
and injective for
$n\geqslant 3$
and injective for
![]() $n=2$
. If
$n=2$
. If
![]() $i$
is weakly regular, it is also an isomorphism for
$i$
is weakly regular, it is also an isomorphism for
![]() $n=2$
.
$n=2$
.
Proof. By flat base change
![]() $H_{n}(A,R,E)=H_{n}(k,R\otimes _{A}k,E)$
, and by the Jacobi–Zariski exact sequence associated to
$H_{n}(A,R,E)=H_{n}(k,R\otimes _{A}k,E)$
, and by the Jacobi–Zariski exact sequence associated to
![]() $k\rightarrow R\otimes _{A}k\rightarrow E$
we have
$k\rightarrow R\otimes _{A}k\rightarrow E$
we have
![]() $H_{n}(k,R\otimes _{A}k,E)=H_{n+1}(R\otimes _{A}k,E,E)=0$
for all
$H_{n}(k,R\otimes _{A}k,E)=H_{n+1}(R\otimes _{A}k,E,E)=0$
for all
![]() $n\geqslant 2$
by Appendix 9. So the Jacobi–Zariski exact sequence
$n\geqslant 2$
by Appendix 9. So the Jacobi–Zariski exact sequence
gives isomorphisms
![]() $H_{n}(A,D,E)=H_{n}(R,D,E)$
for all
$H_{n}(A,D,E)=H_{n}(R,D,E)$
for all
![]() $n\geqslant 3$
and an exact sequence
$n\geqslant 3$
and an exact sequence
The injectivity of
![]() $\unicode[STIX]{x1D6FC}$
when
$\unicode[STIX]{x1D6FC}$
when
![]() $i$
is weakly regular follows from the commutative diagram with exact upper row
$i$
is weakly regular follows from the commutative diagram with exact upper row
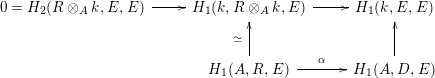
The analogues to Avramov’s theorems [Reference Avramov7, Theorems 1.4, 1.3] are the following two:
Theorem 20. Let
![]() $f:(A,\mathfrak{m},k)\rightarrow (B,\mathfrak{n},l)$
be a local homomorphism of noetherian local rings such that
$f:(A,\mathfrak{m},k)\rightarrow (B,\mathfrak{n},l)$
be a local homomorphism of noetherian local rings such that
![]() $\text{CI}\text{-}\text{dim}(f)<\infty$
. Let
$\text{CI}\text{-}\text{dim}(f)<\infty$
. Let
![]() $m\geqslant 2$
be an integer such that
$m\geqslant 2$
be an integer such that
![]() $(m-1)!$
is invertible in
$(m-1)!$
is invertible in
![]() $B$
. If
$B$
. If
![]() $H_{n}(A,B,l)=0$
for some
$H_{n}(A,B,l)=0$
for some
![]() $n$
with
$n$
with
![]() $3\leqslant n\leqslant 2m-1$
, then
$3\leqslant n\leqslant 2m-1$
, then
![]() $H_{n}(A,B,l)=0$
for all
$H_{n}(A,B,l)=0$
for all
![]() $n\geqslant 3$
.
$n\geqslant 3$
.
Proof. By Appendix 8, we may assume that
![]() $B$
is complete. Consider a diagram
$B$
is complete. Consider a diagram
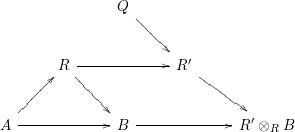
as in the definition of complete intersection dimension. Let
![]() $E$
be the common residue field of
$E$
be the common residue field of
![]() $R^{\prime }$
and
$R^{\prime }$
and
![]() $R^{\prime }\otimes _{R}B$
. By Lemma 19 and flat base change, we have isomorphisms
$R^{\prime }\otimes _{R}B$
. By Lemma 19 and flat base change, we have isomorphisms
for all
![]() $n\geqslant 2$
. Also, from the Jacobi–Zariski exact sequence associated to
$n\geqslant 2$
. Also, from the Jacobi–Zariski exact sequence associated to
![]() $Q\rightarrow R^{\prime }\rightarrow R^{\prime }\otimes _{R}B$
and Appendix 9, we obtain
$Q\rightarrow R^{\prime }\rightarrow R^{\prime }\otimes _{R}B$
and Appendix 9, we obtain
for all
![]() $n\geqslant 3$
.
$n\geqslant 3$
.
Therefore, given an integer
![]() $n\geqslant 3$
,
$n\geqslant 3$
,
![]() $H_{n}(A,B,l)=0$
if and only if
$H_{n}(A,B,l)=0$
if and only if
![]() $H_{n}(Q,R^{\prime }\otimes _{R}B,E)=0$
. Since
$H_{n}(Q,R^{\prime }\otimes _{R}B,E)=0$
. Since
![]() $fd_{Q}(R^{\prime }\otimes _{R}B)<\infty$
, by [Reference Avramov7, Theorem 1.4] (by its proof, that is local, or using [Reference André1, 4.57]) we have
$fd_{Q}(R^{\prime }\otimes _{R}B)<\infty$
, by [Reference Avramov7, Theorem 1.4] (by its proof, that is local, or using [Reference André1, 4.57]) we have
![]() $H_{n}(Q,R^{\prime }\otimes _{R}B,E)=0$
for all
$H_{n}(Q,R^{\prime }\otimes _{R}B,E)=0$
for all
![]() $n\geqslant 2$
, and then
$n\geqslant 2$
, and then
![]() $H_{n}(A,B,l)=0$
for all
$H_{n}(A,B,l)=0$
for all
![]() $n\geqslant 3$
.◻
$n\geqslant 3$
.◻
Theorem 21. Let
![]() $f:(A,\mathfrak{m},k)\rightarrow (B,\mathfrak{n},l)$
be a local homomorphism of noetherian local rings such that
$f:(A,\mathfrak{m},k)\rightarrow (B,\mathfrak{n},l)$
be a local homomorphism of noetherian local rings such that
![]() $\text{CI}\text{-}\text{dim}(f)<\infty$
. If
$\text{CI}\text{-}\text{dim}(f)<\infty$
. If
![]() $H_{n}(A,B,l)=0$
for all
$H_{n}(A,B,l)=0$
for all
![]() $n$
sufficiently large, then
$n$
sufficiently large, then
![]() $H_{n}(A,B,l)=0$
for all
$H_{n}(A,B,l)=0$
for all
![]() $n\geqslant 3$
.
$n\geqslant 3$
.
Proof. It follows from [Reference Avramov7, Theorem 4.4] using the same ideas as in the proof of Theorem 20. ◻
Remark 22. It should be noted that working in a similar way with complete intersection dimension, we can also prove part of [Reference Avramov7, Theorem 1.5] in some very particular cases that are not complete intersection. If
![]() $f:(A,\mathfrak{m},k)\rightarrow (B,\mathfrak{n},l)$
is a local homomorphism of noetherian local rings with
$f:(A,\mathfrak{m},k)\rightarrow (B,\mathfrak{n},l)$
is a local homomorphism of noetherian local rings with
![]() $\text{edim}(A)-\text{depth}(A)\leqslant 3$
or
$\text{edim}(A)-\text{depth}(A)\leqslant 3$
or
![]() $\text{edim}(A)-\text{depth}(A)=4$
and
$\text{edim}(A)-\text{depth}(A)=4$
and
![]() $A$
Gorenstein, the ring
$A$
Gorenstein, the ring
![]() $R$
in a regular factorization (we can assume that
$R$
in a regular factorization (we can assume that
![]() $B$
is complete)
$B$
is complete)
![]() $A\rightarrow R\rightarrow B$
, inherits the same property. If
$A\rightarrow R\rightarrow B$
, inherits the same property. If
![]() $H_{n}(A,B,l)=0$
for all
$H_{n}(A,B,l)=0$
for all
![]() $n$
sufficiently large (and so
$n$
sufficiently large (and so
![]() $H_{n}(R,B,l)=0$
for all
$H_{n}(R,B,l)=0$
for all
![]() $n$
sufficiently large by Lemma 19), and we mimic the proof of [Reference Avramov7, Theorem 4.4] with Quillen’s spectral sequence [Reference Avramov7, p. 475] instead of the spectral sequence of [Reference Avramov7, Theorem 4.2], we conclude that the Poincaré series
$n$
sufficiently large by Lemma 19), and we mimic the proof of [Reference Avramov7, Theorem 4.4] with Quillen’s spectral sequence [Reference Avramov7, p. 475] instead of the spectral sequence of [Reference Avramov7, Theorem 4.2], we conclude that the Poincaré series
has radius of convergence
![]() ${\geqslant}1$
. By [Reference Avramov6], this implies for these particular rings that (the virtual projective dimension and so) the complete intersection dimension of the
${\geqslant}1$
. By [Reference Avramov6], this implies for these particular rings that (the virtual projective dimension and so) the complete intersection dimension of the
![]() $R$
-module
$R$
-module
![]() $B$
is finite. Therefore reasoning as in the proof of Theorem 20, we deduce that
$B$
is finite. Therefore reasoning as in the proof of Theorem 20, we deduce that
![]() $H_{n}(A,B,l)=0$
for all
$H_{n}(A,B,l)=0$
for all
![]() $n\geqslant 3$
.
$n\geqslant 3$
.
Theorem 23. Let

be a commutative square of local homomorphisms of noetherian local rings verifying
-
(i)
 $\text{Tor}_{i}^{A}(\tilde{A},B)=0$
for all
$\text{Tor}_{i}^{A}(\tilde{A},B)=0$
for all
 $i>0$
.
$i>0$
. -
(ii) The homomorphism
 $H_{3}(A,B,\tilde{l})\rightarrow H_{3}(\tilde{A},\tilde{B},\tilde{l})$
vanishes.
$H_{3}(A,B,\tilde{l})\rightarrow H_{3}(\tilde{A},\tilde{B},\tilde{l})$
vanishes. -
(iii) If
 $\mathfrak{p}$
is the contraction in
$\mathfrak{p}$
is the contraction in
 $\tilde{A}\otimes _{A}B$
of the maximal ideal
$\tilde{A}\otimes _{A}B$
of the maximal ideal
 $\tilde{\mathfrak{n}}$
of
$\tilde{\mathfrak{n}}$
of
 $\tilde{B}$
, then
$\tilde{B}$
, then
 $(\tilde{A}\otimes _{A}B)_{\mathfrak{p}}$
is a noetherian ring.
$(\tilde{A}\otimes _{A}B)_{\mathfrak{p}}$
is a noetherian ring. -
(iv) If
 $\unicode[STIX]{x1D714}$
is the homomorphism
$\unicode[STIX]{x1D714}$
is the homomorphism
 $(\tilde{A}\otimes _{A}B)_{\mathfrak{p}}\rightarrow \tilde{B}$
, then
$(\tilde{A}\otimes _{A}B)_{\mathfrak{p}}\rightarrow \tilde{B}$
, then
 $\text{cidim}(\unicode[STIX]{x1D714})<\infty$
.
$\text{cidim}(\unicode[STIX]{x1D714})<\infty$
.
Then
![]() $H_{3}(A,B,l)=0$
.
$H_{3}(A,B,l)=0$
.
Proof. We can assume that
![]() $\tilde{B}$
is complete. Consider a diagram showing that cidim
$\tilde{B}$
is complete. Consider a diagram showing that cidim
![]() $(\unicode[STIX]{x1D714})<\infty$
$(\unicode[STIX]{x1D714})<\infty$
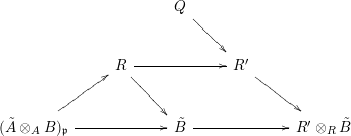
Let
![]() $E$
be the residue field of
$E$
be the residue field of
![]() $R^{\prime }$
and
$R^{\prime }$
and
![]() $R^{\prime }\otimes _{R}\tilde{B}$
. We have
$R^{\prime }\otimes _{R}\tilde{B}$
. We have
for all
![]() $n\geqslant 3$
, by Lemma 19 and flat base change.
$n\geqslant 3$
, by Lemma 19 and flat base change.
Using [Reference André1, 19.21, 20.26, 20.27] to interpret [Reference Avramov4] in terms of André–Quillen homology, since
![]() $fd_{Q}(R^{\prime }\otimes _{R}\tilde{B})<\infty$
, we have a zero homomorphism in the upper row of the commutative diagram
$fd_{Q}(R^{\prime }\otimes _{R}\tilde{B})<\infty$
, we have a zero homomorphism in the upper row of the commutative diagram

where for the isomorphisms we have used again Lemma 19, and Appendix 4, 9, having in mind that
![]() $R\rightarrow R^{\prime }$
is flat with complete intersection closed fiber. We obtain that the map
$R\rightarrow R^{\prime }$
is flat with complete intersection closed fiber. We obtain that the map
is zero.
Using hypotheses (i) and (ii) and Appendix 3, 4, we have a commutative diagram
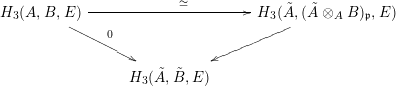
showing that the homomorphism
![]() $H_{3}(\tilde{A},(\tilde{A}\otimes _{A}B)_{\mathfrak{p}},E)\rightarrow H_{3}(\tilde{A},\tilde{B},E)$
is zero. So from the Jacobi–Zariski exact sequence
$H_{3}(\tilde{A},(\tilde{A}\otimes _{A}B)_{\mathfrak{p}},E)\rightarrow H_{3}(\tilde{A},\tilde{B},E)$
is zero. So from the Jacobi–Zariski exact sequence
we deduce that
![]() $\unicode[STIX]{x1D6FF}$
is surjective. Therefore we have a commutative diagram
$\unicode[STIX]{x1D6FF}$
is surjective. Therefore we have a commutative diagram

from which we deduce that
We can point out special cases of this theorem as we did in
![]() $A-E$
in Section 1. In particular, using Corollary 12 and Theorem 23, we can extend the main results in [Reference Blanco and Majadas15] from the Frobenius homomorphism to contracting endomorphisms. All works along the same lines, so we content ourselves with the following two criteria for complete intersection homomorphisms.
$A-E$
in Section 1. In particular, using Corollary 12 and Theorem 23, we can extend the main results in [Reference Blanco and Majadas15] from the Frobenius homomorphism to contracting endomorphisms. All works along the same lines, so we content ourselves with the following two criteria for complete intersection homomorphisms.
The reader may consult the definitions and properties of complete intersection homomorphisms and quasicomplete intersection homomorphisms in [Reference Avramov7, Reference Avramov, Henriques and Şega10], where they have been studied in depth. We only need here their characterization in terms of André–Quillen homology. If
![]() $f:(A,\mathfrak{m},k)\rightarrow (B,\mathfrak{n},l)$
is a local homomorphism of noetherian local rings,
$f:(A,\mathfrak{m},k)\rightarrow (B,\mathfrak{n},l)$
is a local homomorphism of noetherian local rings,
![]() $f$
is complete intersection at
$f$
is complete intersection at
![]() $\mathfrak{n}$
if and only if
$\mathfrak{n}$
if and only if
![]() $H_{n}(A,B,l)=0$
for all
$H_{n}(A,B,l)=0$
for all
![]() $n\geqslant 2$
[Reference Avramov7, Proposition 1.1], and is quasicomplete intersection at
$n\geqslant 2$
[Reference Avramov7, Proposition 1.1], and is quasicomplete intersection at
![]() $\mathfrak{n}$
if and only if
$\mathfrak{n}$
if and only if
![]() $H_{n}(A,B,l)=0$
for all
$H_{n}(A,B,l)=0$
for all
![]() $n\geqslant 3$
[Reference Avramov, Henriques and Şega10, 8.5]. We will consider these properties always at the maximal ideals of the rings involved, so again we will suppress “at
$n\geqslant 3$
[Reference Avramov, Henriques and Şega10, 8.5]. We will consider these properties always at the maximal ideals of the rings involved, so again we will suppress “at
![]() $\mathfrak{n}$
” from the notation. Note that this terminology is congruent with the notion of flat complete intersection homomorphism defined at the beginning of this section, since if
$\mathfrak{n}$
” from the notation. Note that this terminology is congruent with the notion of flat complete intersection homomorphism defined at the beginning of this section, since if
![]() $f$
is flat, then
$f$
is flat, then
for
![]() $n\geqslant 2$
by Appendix 4, 6, 7, and
$n\geqslant 2$
by Appendix 4, 6, 7, and
![]() $H_{n+1}(B\otimes _{A}k,l,l)=0$
for
$H_{n+1}(B\otimes _{A}k,l,l)=0$
for
![]() $n\geqslant 2$
if and only if
$n\geqslant 2$
if and only if
![]() $B\otimes _{A}k$
is a complete intersection ring (Appendix 9).
$B\otimes _{A}k$
is a complete intersection ring (Appendix 9).
Corollary 24. Let
![]() $A\xrightarrow[{}]{u}B\xrightarrow[{}]{v}C$
be local homomorphisms of noetherian local rings such that
$A\xrightarrow[{}]{u}B\xrightarrow[{}]{v}C$
be local homomorphisms of noetherian local rings such that
![]() $\text{cidim}(v)<\infty$
. Assume that the characteristic of the residue fields is
$\text{cidim}(v)<\infty$
. Assume that the characteristic of the residue fields is
![]() $\neq 2$
. If
$\neq 2$
. If
![]() $vu$
is quasicomplete intersection (resp. complete intersection) then
$vu$
is quasicomplete intersection (resp. complete intersection) then
![]() $u$
is quasicomplete intersection (resp. complete intersection) and
$u$
is quasicomplete intersection (resp. complete intersection) and
![]() $v$
is quasicomplete intersection.
$v$
is quasicomplete intersection.
Proof. Let
![]() $E$
be the residue field of
$E$
be the residue field of
![]() $C$
. We apply Theorem 23 to
$C$
. We apply Theorem 23 to

and we obtain
![]() $H_{3}(A,B,E)=0$
. Then, from the Jacobi–Zariski exact sequence
$H_{3}(A,B,E)=0$
. Then, from the Jacobi–Zariski exact sequence
we deduce
![]() $H_{4}(B,C,E)=0$
, and so from Theorem 20 we get
$H_{4}(B,C,E)=0$
, and so from Theorem 20 we get
for all
![]() $n\geqslant 3$
, that is,
$n\geqslant 3$
, that is,
![]() $v$
is quasicomplete intersection.
$v$
is quasicomplete intersection.
Again from the same Jacobi–Zariski exact sequence
we deduce
![]() $H_{n}(A,B,E)=0$
for all
$H_{n}(A,B,E)=0$
for all
![]() $n\geqslant 3$
(resp. for all
$n\geqslant 3$
(resp. for all
![]() $n\geqslant 2$
).◻
$n\geqslant 2$
).◻
In the particular case when
![]() $fd_{B}(C)<\infty$
this result was proved in [Reference Avramov7, 5.7.1] for the case of complete intersection and in [Reference Avramov, Henriques and Şega10, 8.9] for quasicomplete intersection (even in characteristic 2).
$fd_{B}(C)<\infty$
this result was proved in [Reference Avramov7, 5.7.1] for the case of complete intersection and in [Reference Avramov, Henriques and Şega10, 8.9] for quasicomplete intersection (even in characteristic 2).
Corollary 25. Let
![]() $u:(A,\mathfrak{m},k)\rightarrow (B,\mathfrak{n},l)$
be a local flat homomorphism of noetherian local rings and
$u:(A,\mathfrak{m},k)\rightarrow (B,\mathfrak{n},l)$
be a local flat homomorphism of noetherian local rings and
![]() $\unicode[STIX]{x1D714}:B\otimes _{A}B\rightarrow B$
the multiplication map. Let
$\unicode[STIX]{x1D714}:B\otimes _{A}B\rightarrow B$
the multiplication map. Let
![]() $\mathfrak{p}=\unicode[STIX]{x1D714}^{-1}(\mathfrak{n})$
and assume that
$\mathfrak{p}=\unicode[STIX]{x1D714}^{-1}(\mathfrak{n})$
and assume that
![]() $(B\otimes _{A}B)_{\mathfrak{p}}$
is noetherian. If
$(B\otimes _{A}B)_{\mathfrak{p}}$
is noetherian. If
![]() $\text{cidim}_{(B\otimes _{A}B)_{\mathfrak{p}}}(B)<\infty$
, then
$\text{cidim}_{(B\otimes _{A}B)_{\mathfrak{p}}}(B)<\infty$
, then
![]() $u$
is complete intersection (at
$u$
is complete intersection (at
![]() $\mathfrak{n}$
).
$\mathfrak{n}$
).
Proof. By Theorem 23 applied to
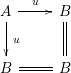
we obtain
![]() $H_{3}(A,B,l)=0$
, and since
$H_{3}(A,B,l)=0$
, and since
![]() $u$
is flat, we deduce from [Reference André1, 17.2] that
$u$
is flat, we deduce from [Reference André1, 17.2] that
![]() $H_{n}(A,B,l)=0$
for all
$H_{n}(A,B,l)=0$
for all
![]() $n\geqslant 2$
.◻
$n\geqslant 2$
.◻
Remark 26. Similarly to Remark 16, this result is also valid more generally for a noetherian supplemented
![]() $B$
-algebra
$B$
-algebra
![]() $S$
instead of
$S$
instead of
![]() $B\otimes _{A}B$
. If cidim
$B\otimes _{A}B$
. If cidim
![]() $_{S_{\mathfrak{p}}}(B)<\infty$
, where
$_{S_{\mathfrak{p}}}(B)<\infty$
, where
![]() $\mathfrak{p}$
is the contraction in
$\mathfrak{p}$
is the contraction in
![]() $S$
of the maximal ideal of
$S$
of the maximal ideal of
![]() $B$
, we apply Theorem 23 to the square
$B$
, we apply Theorem 23 to the square

We obtain
![]() $H_{3}(B,S_{\mathfrak{p}},l)=0$
, and so from the Jacobi–Zariski exact sequence associated to
$H_{3}(B,S_{\mathfrak{p}},l)=0$
, and so from the Jacobi–Zariski exact sequence associated to
![]() $B\rightarrow S_{\mathfrak{p}}\rightarrow B$
we deduce
$B\rightarrow S_{\mathfrak{p}}\rightarrow B$
we deduce
![]() $H_{4}(S_{\mathfrak{p}},B,l)=0$
. By Theorem 20 (in characteristic
$H_{4}(S_{\mathfrak{p}},B,l)=0$
. By Theorem 20 (in characteristic
![]() $\neq 2$
),
$\neq 2$
),
![]() $H_{n}(S_{\mathfrak{p}},B,l)=0$
for all
$H_{n}(S_{\mathfrak{p}},B,l)=0$
for all
![]() $n\geqslant 3$
, and then from [Reference André1, 4.57] we deduce
$n\geqslant 3$
, and then from [Reference André1, 4.57] we deduce
![]() $H_{n}(S_{\mathfrak{p}},B,-)=0$
for all
$H_{n}(S_{\mathfrak{p}},B,-)=0$
for all
![]() $n\geqslant 3$
.
$n\geqslant 3$
.
In fact, the hypothesis on the characteristic is not necessary since by [Reference Avramov and Iyengar12, Theorem I], for a noetherian supplemented
![]() $B$
-algebra
$B$
-algebra
![]() $S$
,
$S$
,
![]() $H_{4}(S,B,-)=0$
implies
$H_{4}(S,B,-)=0$
implies
![]() $H_{n}(S,B,-)=0$
for all
$H_{n}(S,B,-)=0$
for all
![]() $n\geqslant 3$
(a direct proof of this fact was communicated to me by Rodicio: we can assume that the rings are local and complete; take a regular factorization
$n\geqslant 3$
(a direct proof of this fact was communicated to me by Rodicio: we can assume that the rings are local and complete; take a regular factorization
![]() $B\rightarrow R\rightarrow S$
; we have
$B\rightarrow R\rightarrow S$
; we have
![]() $H_{3}(B,S,-)=H_{4}(S,B,-)=0$
and so
$H_{3}(B,S,-)=H_{4}(S,B,-)=0$
and so
![]() $H_{3}(R,S,-)=0$
by Lemma 19; using this same Lemma, we have
$H_{3}(R,S,-)=0$
by Lemma 19; using this same Lemma, we have
![]() $H_{n}(R,B,-)=H_{n}(B,B,-)=0$
for all
$H_{n}(R,B,-)=H_{n}(B,B,-)=0$
for all
![]() $n\geqslant 2$
; in the commutative diagram with exact row
$n\geqslant 2$
; in the commutative diagram with exact row
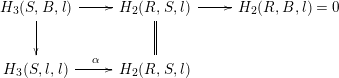
we have
![]() $\unicode[STIX]{x1D6FC}=0$
by [Reference Rodicio28, Corollary 6] and then
$\unicode[STIX]{x1D6FC}=0$
by [Reference Rodicio28, Corollary 6] and then
![]() $H_{2}(R,S,l)=0$
; this implies
$H_{2}(R,S,l)=0$
; this implies
![]() $H_{n}(R,S,l)=0$
for all
$H_{n}(R,S,l)=0$
for all
![]() $n\geqslant 2$
by Appendix 9 and then
$n\geqslant 2$
by Appendix 9 and then
![]() $H_{n}(B,S,l)=0$
for all
$H_{n}(B,S,l)=0$
for all
![]() $n\geqslant 2$
by Lemma 19; since
$n\geqslant 2$
by Lemma 19; since
![]() $H_{n+1}(S,B,l)=H_{n}(B,S,l)$
we deduce
$H_{n+1}(S,B,l)=H_{n}(B,S,l)$
we deduce
![]() $H_{n}(S,B,-)=0$
for all
$H_{n}(S,B,-)=0$
for all
![]() $n\geqslant 3$
).
$n\geqslant 3$
).
Acknowledgments
We thank the referee for a careful reading of the paper and for pointing out a mistake in an earlier version.
Appendix: Some results on André–Quillen homology used in the proofs
Associated to a homomorphism of (commutative) rings
![]() $f:A\rightarrow B$
and to a
$f:A\rightarrow B$
and to a
![]() $B$
-module
$B$
-module
![]() $M$
we have (André–Quillen) homology
$M$
we have (André–Quillen) homology
![]() $B$
-modules
$B$
-modules
![]() $H_{n}(A,B,M)$
for all integers
$H_{n}(A,B,M)$
for all integers
![]() $n\geqslant 0$
, which are functorial in all three variables and satisfy the following properties:
$n\geqslant 0$
, which are functorial in all three variables and satisfy the following properties:
-
1. If
 $B=A/I$
, then
$B=A/I$
, then
 $H_{0}(A,B,M)=0$
[Reference André1, 4.60].
$H_{0}(A,B,M)=0$
[Reference André1, 4.60]. -
2. If
 $0\rightarrow M^{\prime }\rightarrow M\rightarrow M^{\prime \prime }\rightarrow 0$
is an exact sequence of
$0\rightarrow M^{\prime }\rightarrow M\rightarrow M^{\prime \prime }\rightarrow 0$
is an exact sequence of
 $B$
-modules, we have a natural exact sequence [Reference André1, 3.22]
$B$
-modules, we have a natural exact sequence [Reference André1, 3.22]  $$\begin{eqnarray}\begin{array}{@{}r@{}}\cdots \rightarrow H_{n+1}(A,B,M^{\prime \prime })\rightarrow \\ H_{n}(A,B,M^{\prime })\rightarrow H_{n}(A,B,M)\rightarrow H_{n}(A,B,M^{\prime \prime })\rightarrow \\ H_{n-1}(A,B,M^{\prime })\rightarrow \cdots \rightarrow H_{0}(A,B,M^{\prime \prime })\rightarrow 0\end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}r@{}}\cdots \rightarrow H_{n+1}(A,B,M^{\prime \prime })\rightarrow \\ H_{n}(A,B,M^{\prime })\rightarrow H_{n}(A,B,M)\rightarrow H_{n}(A,B,M^{\prime \prime })\rightarrow \\ H_{n-1}(A,B,M^{\prime })\rightarrow \cdots \rightarrow H_{0}(A,B,M^{\prime \prime })\rightarrow 0\end{array}\end{eqnarray}$$
-
3. (Localization) Let
 $u:A\rightarrow B$
be a ring homomorphism,
$u:A\rightarrow B$
be a ring homomorphism,
 $T$
a multiplicative subset of
$T$
a multiplicative subset of
 $B$
,
$B$
,
 $S$
a multiplicative subset of
$S$
a multiplicative subset of
 $A$
such that
$A$
such that
 $u(S)\subset T$
, and
$u(S)\subset T$
, and
 $M$
a
$M$
a
 $B$
-module. Then [Reference André1, 4, 59, 5.27]
$B$
-module. Then [Reference André1, 4, 59, 5.27]  $$\begin{eqnarray}\displaystyle T^{-1}H_{n}(A,B,M) & = & \displaystyle H_{n}(A,B,T^{-1}M)\nonumber\\ \displaystyle & = & \displaystyle H_{n}(A,T^{-1}B,T^{-1}M)=H_{n}(S^{-1}A,T^{-1}B,T^{-1}M).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle T^{-1}H_{n}(A,B,M) & = & \displaystyle H_{n}(A,B,T^{-1}M)\nonumber\\ \displaystyle & = & \displaystyle H_{n}(A,T^{-1}B,T^{-1}M)=H_{n}(S^{-1}A,T^{-1}B,T^{-1}M).\nonumber\end{eqnarray}$$
-
4. (Base change) Let
 $A\rightarrow B$
,
$A\rightarrow B$
,
 $A\rightarrow C$
be ring homomorphisms such that
$A\rightarrow C$
be ring homomorphisms such that
 $\text{Tor}_{i}^{A}(B,C)=0$
for all
$\text{Tor}_{i}^{A}(B,C)=0$
for all
 $i>0$
, and let
$i>0$
, and let
 $M$
be a
$M$
be a
 $B\otimes _{A}C$
-module. Then
$B\otimes _{A}C$
-module. Then
 $H_{n}(A,B,M)=H_{n}(C,B\otimes _{A}C,M)$
for all
$H_{n}(A,B,M)=H_{n}(C,B\otimes _{A}C,M)$
for all
 $n$
[Reference André1, 4.54].
$n$
[Reference André1, 4.54]. -
5. Let
 $B$
be an
$B$
be an
 $A$
-algebra,
$A$
-algebra,
 $C$
a
$C$
a
 $B$
-algebra and
$B$
-algebra and
 $M$
a flat
$M$
a flat
 $C$
-module. Then
$C$
-module. Then
 $H_{n}(A,B,M)=H_{n}(A,B,C)\otimes _{C}M$
for all
$H_{n}(A,B,M)=H_{n}(A,B,C)\otimes _{C}M$
for all
 $n$
[Reference André1, 3.20].
$n$
[Reference André1, 3.20]. -
6. (Jacobi–Zariski exact sequence) If
 $A\rightarrow B\rightarrow C$
are ring homomorphisms and
$A\rightarrow B\rightarrow C$
are ring homomorphisms and
 $M$
is a
$M$
is a
 $C$
-module, we have a natural exact sequence [Reference André1, 5.1]
$C$
-module, we have a natural exact sequence [Reference André1, 5.1]  $$\begin{eqnarray}\begin{array}{@{}r@{}}\cdots \rightarrow H_{n+1}(B,C,M)\rightarrow \\ H_{n}(A,B,M)\rightarrow H_{n}(A,C,M)\rightarrow H_{n}(B,C,M)\rightarrow \\ H_{n-1}(A,B,M)\rightarrow \cdots \rightarrow H_{0}(B,C,M)\rightarrow 0\end{array}\end{eqnarray}$$
$$\begin{eqnarray}\begin{array}{@{}r@{}}\cdots \rightarrow H_{n+1}(B,C,M)\rightarrow \\ H_{n}(A,B,M)\rightarrow H_{n}(A,C,M)\rightarrow H_{n}(B,C,M)\rightarrow \\ H_{n-1}(A,B,M)\rightarrow \cdots \rightarrow H_{0}(B,C,M)\rightarrow 0\end{array}\end{eqnarray}$$
-
7. If
 $K\rightarrow L$
is a field extension and
$K\rightarrow L$
is a field extension and
 $M$
an
$M$
an
 $L$
-module, we have
$L$
-module, we have
 $H_{n}(K,L,M)=0$
for all
$H_{n}(K,L,M)=0$
for all
 $n\geqslant 2$
[Reference André1, 7.4]. So if
$n\geqslant 2$
[Reference André1, 7.4]. So if
 $A\rightarrow K\rightarrow L$
are ring homomorphisms with
$A\rightarrow K\rightarrow L$
are ring homomorphisms with
 $K$
and
$K$
and
 $L$
fields, from 6 we obtain for all
$L$
fields, from 6 we obtain for all $$\begin{eqnarray}H_{n}(A,K,L)=H_{n}(A,L,L)\end{eqnarray}$$
$$\begin{eqnarray}H_{n}(A,K,L)=H_{n}(A,L,L)\end{eqnarray}$$
 $n\geqslant 2$
, which, using 5, gives
$n\geqslant 2$
, which, using 5, gives
 $H_{n}(A,K,K)\otimes _{K}L=H_{n}(A,L,L)$
for all
$H_{n}(A,K,K)\otimes _{K}L=H_{n}(A,L,L)$
for all
 $n\geqslant 2$
.
$n\geqslant 2$
.
-
8. If
 $(A,\mathfrak{m},k)$
is a noetherian local ring and
$(A,\mathfrak{m},k)$
is a noetherian local ring and
 $\hat{A}$
is its
$\hat{A}$
is its
 $\mathfrak{m}$
-completion, then
$\mathfrak{m}$
-completion, then
 $H_{n}(A,k,k)=H_{n}(\hat{A},k,k)$
for all
$H_{n}(A,k,k)=H_{n}(\hat{A},k,k)$
for all
 $n\geqslant 0$
[Reference André1, 10.18]. As a consequence, if
$n\geqslant 0$
[Reference André1, 10.18]. As a consequence, if
 $(A,\mathfrak{m},k)\rightarrow (B,\mathfrak{n},l)$
is a local homomorphism of noetherian local rings, then taking the map between the Jacobi–Zariski exact sequences associated to
$(A,\mathfrak{m},k)\rightarrow (B,\mathfrak{n},l)$
is a local homomorphism of noetherian local rings, then taking the map between the Jacobi–Zariski exact sequences associated to
 $A\rightarrow B\rightarrow l$
and
$A\rightarrow B\rightarrow l$
and
 $\hat{A}\rightarrow \hat{B}\rightarrow l$
, we deduce that
$\hat{A}\rightarrow \hat{B}\rightarrow l$
, we deduce that  $$\begin{eqnarray}H_{n}(A,B,l)=H_{n}(\hat{A},\hat{B},l).\end{eqnarray}$$
$$\begin{eqnarray}H_{n}(A,B,l)=H_{n}(\hat{A},\hat{B},l).\end{eqnarray}$$
-
9. If
 $I$
is an ideal of a noetherian local ring
$I$
is an ideal of a noetherian local ring
 $(A,\mathfrak{m},k)$
, then the following are equivalent:
$(A,\mathfrak{m},k)$
, then the following are equivalent:-
(i)
 $I$
is generated by a regular sequence.
$I$
is generated by a regular sequence. -
(ii)
 $H_{2}(A,A/I,k)=0$
.
$H_{2}(A,A/I,k)=0$
. -
(iii)
 $H_{n}(A,A/I,M)=0$
for any
$H_{n}(A,A/I,M)=0$
for any
 $A/I$
-module
$A/I$
-module
 $M$
for all
$M$
for all
 $n\geqslant 2$
[Reference André1, 6.25].
$n\geqslant 2$
[Reference André1, 6.25].
In particular, a noetherian local ring
 $(A,\mathfrak{m},k)$
is regular if and only if
$(A,\mathfrak{m},k)$
is regular if and only if
 $H_{2}(A,k,k)=0$
.
$H_{2}(A,k,k)=0$
.Similarly, a noetherian local ring
 $(A,\mathfrak{m},k)$
is complete intersection if and only if
$(A,\mathfrak{m},k)$
is complete intersection if and only if
 $H_{3}(A,k,k)=0$
if and only if
$H_{3}(A,k,k)=0$
if and only if
 $H_{n}(A,k,k)=0$
for all
$H_{n}(A,k,k)=0$
for all
 $n\geqslant 3$
[Reference André1, 6.27 and its proof].
$n\geqslant 3$
[Reference André1, 6.27 and its proof].Finally, two important results by André and Avramov resp. that play a key role in this paper:
-
-
10. A local homomorphism of noetherian local rings
 $(A,\mathfrak{m},k)\rightarrow (B,\mathfrak{n},l)$
is formally smooth (for the
$(A,\mathfrak{m},k)\rightarrow (B,\mathfrak{n},l)$
is formally smooth (for the
 $\mathfrak{n}$
-adic topology) in the sense of [Reference Grothendieck19,
$\mathfrak{n}$
-adic topology) in the sense of [Reference Grothendieck19,
 $0_{IV}19.3.1$
] if and only if
$0_{IV}19.3.1$
] if and only if
 $H_{1}(A,B,l)=0$
(essentially [Reference André1, 16.17]; use [Reference André1, 3.21]).
$H_{1}(A,B,l)=0$
(essentially [Reference André1, 16.17]; use [Reference André1, 3.21]). -
11. The main result in [Reference Avramov4] can be read in terms of André–Quillen homology as follows (see [Reference André1, 19.21, 20.26]): if
 $(A,\mathfrak{m},k)\rightarrow (B,\mathfrak{n},l)$
is a local homomorphism of finite flat dimension of noetherian local rings, then the homomorphism
$(A,\mathfrak{m},k)\rightarrow (B,\mathfrak{n},l)$
is a local homomorphism of finite flat dimension of noetherian local rings, then the homomorphism
 $H_{2}(A,l,l)\rightarrow H_{2}(B,l,l)$
is injective.
$H_{2}(A,l,l)\rightarrow H_{2}(B,l,l)$
is injective.



