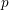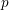Introduction
Let
![]() $R$
be a normal complete noetherian local ring with perfect residue field
$R$
be a normal complete noetherian local ring with perfect residue field
![]() $k$
of positive characteristic
$k$
of positive characteristic
![]() $p$
and with fraction field
$p$
and with fraction field
![]() $K$
of characteristic zero. For a
$K$
of characteristic zero. For a
![]() $p$
-divisible group
$p$
-divisible group
![]() $G$
over
$G$
over
![]() $R$
, the Tate module
$R$
, the Tate module
![]() $T_{p}(G)$
is a free
$T_{p}(G)$
is a free
![]() $\mathbb{Z}_{p}$
-module of finite rank with a continuous action of the absolute Galois group
$\mathbb{Z}_{p}$
-module of finite rank with a continuous action of the absolute Galois group
![]() ${\mathcal{G}}_{K}$
. We want to describe the Tate module in terms of the Dieudonné display
${\mathcal{G}}_{K}$
. We want to describe the Tate module in terms of the Dieudonné display
![]() $\mathscr{P}=(P,Q,F,F_{1})$
associated to
$\mathscr{P}=(P,Q,F,F_{1})$
associated to
![]() $G$
in [Reference ZinkZi2, Reference LauLa3], and relate this to other descriptions of the Tate module when
$G$
in [Reference ZinkZi2, Reference LauLa3], and relate this to other descriptions of the Tate module when
![]() $R$
is a discrete valuation ring.
$R$
is a discrete valuation ring.
Let us recall the notion of a Dieudonné display. The Zink ring
![]() $\mathbb{W}(R)$
is a certain subring of the ring of Witt vectors
$\mathbb{W}(R)$
is a certain subring of the ring of Witt vectors
![]() $W(R)$
which is stable under the Frobenius endomorphism
$W(R)$
which is stable under the Frobenius endomorphism
![]() $f$
of
$f$
of
![]() $W(R)$
. The components of
$W(R)$
. The components of
![]() $\mathscr{P}$
are
$\mathscr{P}$
are
![]() $\mathbb{W}(R)$
-modules
$\mathbb{W}(R)$
-modules
![]() $Q\subseteq P$
where
$Q\subseteq P$
where
![]() $P$
is finite free and
$P$
is finite free and
![]() $P/Q$
is a free
$P/Q$
is a free
![]() $R$
-module, and
$R$
-module, and
![]() $f$
-linear maps
$f$
-linear maps
![]() $F:P\rightarrow P$
and
$F:P\rightarrow P$
and
![]() $F_{1}:Q\rightarrow P$
such that
$F_{1}:Q\rightarrow P$
such that
![]() $F_{1}(Q)$
generates
$F_{1}(Q)$
generates
![]() $P$
and
$P$
and
![]() $F_{1}(v(u_{0}a)x)=aF(x)$
for
$F_{1}(v(u_{0}a)x)=aF(x)$
for
![]() $x\in P$
and
$x\in P$
and
![]() $a\in \mathbb{W}(R)$
. Here
$a\in \mathbb{W}(R)$
. Here
![]() $v$
is the Verschiebung of
$v$
is the Verschiebung of
![]() $W(R)$
, and
$W(R)$
, and
![]() $u_{0}\in W(R)$
is the unit defined by
$u_{0}\in W(R)$
is the unit defined by
![]() $u_{0}=1$
if
$u_{0}=1$
if
![]() $p\geqslant 3$
and by
$p\geqslant 3$
and by
![]() $v(u_{0})=2-[2]$
if
$v(u_{0})=2-[2]$
if
![]() $p=2$
. The twist by
$p=2$
. The twist by
![]() $u_{0}$
is necessary since
$u_{0}$
is necessary since
![]() $v$
does not stabilize
$v$
does not stabilize
![]() $\mathbb{W}(R)$
when
$\mathbb{W}(R)$
when
![]() $p=2$
.
$p=2$
.
To state the main result we need the following scalar extension of
![]() $\mathscr{P}$
. Let
$\mathscr{P}$
. Let
![]() $\hat{R}^{\operatorname{nr}}$
be the completion of the strict Henselization of
$\hat{R}^{\operatorname{nr}}$
be the completion of the strict Henselization of
![]() $R$
, let
$R$
, let
![]() $\tilde{K}$
be an algebraic closure of the fraction field
$\tilde{K}$
be an algebraic closure of the fraction field
![]() $\hat{K}^{\operatorname{nr}}$
of
$\hat{K}^{\operatorname{nr}}$
of
![]() $\hat{R}^{\operatorname{nr}}$
, and let
$\hat{R}^{\operatorname{nr}}$
, and let
![]() $\tilde{R}\subset \tilde{K}$
be the integral closure of
$\tilde{R}\subset \tilde{K}$
be the integral closure of
![]() $\hat{R}^{\operatorname{nr}}$
. We define
$\hat{R}^{\operatorname{nr}}$
. We define
where
![]() $E$
runs through the finite extensions of
$E$
runs through the finite extensions of
![]() $\hat{K}^{\operatorname{nr}}$
in
$\hat{K}^{\operatorname{nr}}$
in
![]() $\tilde{K}$
and where
$\tilde{K}$
and where
![]() $R_{E}=\tilde{R}\cap E$
. Let
$R_{E}=\tilde{R}\cap E$
. Let
![]() $\tilde{R}^{\wedge }$
and
$\tilde{R}^{\wedge }$
and
![]() $\hat{\mathbb{W}}(\tilde{R})$
be the
$\hat{\mathbb{W}}(\tilde{R})$
be the
![]() $p$
-adic completions of
$p$
-adic completions of
![]() $\tilde{R}$
and
$\tilde{R}$
and
![]() $\mathbb{W}(\tilde{R})$
. We define
$\mathbb{W}(\tilde{R})$
. We define
and
Let
![]() $\bar{K}$
be the algebraic closure of
$\bar{K}$
be the algebraic closure of
![]() $K$
in
$K$
in
![]() $\tilde{K}$
and let
$\tilde{K}$
and let
![]() $\tilde{{\mathcal{G}}}_{K}$
be the group of automorphisms of
$\tilde{{\mathcal{G}}}_{K}$
be the group of automorphisms of
![]() $\tilde{K}$
whose restriction to
$\tilde{K}$
whose restriction to
![]() $\bar{K}\hat{K}^{\operatorname{nr}}$
is induced by an element of
$\bar{K}\hat{K}^{\operatorname{nr}}$
is induced by an element of
![]() ${\mathcal{G}}_{K}$
. The natural map
${\mathcal{G}}_{K}$
. The natural map
![]() $\tilde{{\mathcal{G}}}_{K}\rightarrow {\mathcal{G}}_{K}$
is surjective, and bijective when
$\tilde{{\mathcal{G}}}_{K}\rightarrow {\mathcal{G}}_{K}$
is surjective, and bijective when
![]() $R$
is one-dimensional since then
$R$
is one-dimensional since then
![]() $\tilde{K}=\bar{K}\hat{K}^{\operatorname{nr}}$
. The following is the main result of this note; see Proposition 4.1.
$\tilde{K}=\bar{K}\hat{K}^{\operatorname{nr}}$
. The following is the main result of this note; see Proposition 4.1.
Theorem A. There is an exact sequence of
![]() $\tilde{{\mathcal{G}}}_{K}$
-modules
$\tilde{{\mathcal{G}}}_{K}$
-modules
Here
![]() $F_{1}$
is a natural extension of
$F_{1}$
is a natural extension of
![]() $F_{1}:Q\rightarrow P$
. If
$F_{1}:Q\rightarrow P$
. If
![]() $G$
is connected, a similar description of
$G$
is connected, a similar description of
![]() $T_{p}(G)$
in terms of the nilpotent display of
$T_{p}(G)$
in terms of the nilpotent display of
![]() $G$
is part of Zink’s theory of displays. In this case
$G$
is part of Zink’s theory of displays. In this case
![]() $k$
need not be perfect; see [Reference MessingMe2, Proposition 4.4]. The proof is recalled in Proposition 2.1 below.
$k$
need not be perfect; see [Reference MessingMe2, Proposition 4.4]. The proof is recalled in Proposition 2.1 below.
The one-dimensional case
Assume now in addition that
![]() $R$
is a discrete valuation ring. Then Theorem A can be related to the descriptions of
$R$
is a discrete valuation ring. Then Theorem A can be related to the descriptions of
![]() $T_{p}(G)$
in terms of
$T_{p}(G)$
in terms of
![]() $p$
-adic Hodge theory and in terms of Breuil–Kisin modules as follows.
$p$
-adic Hodge theory and in terms of Breuil–Kisin modules as follows.
Relation with the crystalline period homomorphism
Let
![]() $M_{\operatorname{cris}}$
be the value of the covariant Dieudonné crystal of
$M_{\operatorname{cris}}$
be the value of the covariant Dieudonné crystal of
![]() $G$
over
$G$
over
![]() $A_{\operatorname{cris}}(\bar{R})$
. It carries a filtration and a Frobenius, and by [Reference FaltingsFa] there is a period homomorphism
$A_{\operatorname{cris}}(\bar{R})$
. It carries a filtration and a Frobenius, and by [Reference FaltingsFa] there is a period homomorphism
which is bijective if
![]() $p\geqslant 3$
, and injective with cokernel annihilated by
$p\geqslant 3$
, and injective with cokernel annihilated by
![]() $p$
if
$p$
if
![]() $p=2$
. The
$p=2$
. The
![]() $v$
-stabilized Zink ring
$v$
-stabilized Zink ring
![]() $\mathbb{W}^{+}(R)=\mathbb{W}(R)[v(1)]$
studied in [Reference LauLa3] induces an extension
$\mathbb{W}^{+}(R)=\mathbb{W}(R)[v(1)]$
studied in [Reference LauLa3] induces an extension
![]() $\hat{\mathbb{W}}^{+}(\tilde{R})$
of the ring
$\hat{\mathbb{W}}^{+}(\tilde{R})$
of the ring
![]() $\hat{\mathbb{W}}(\tilde{R})$
defined above, which is the trivial extension when
$\hat{\mathbb{W}}(\tilde{R})$
defined above, which is the trivial extension when
![]() $p\geqslant 3$
. The universal property of
$p\geqslant 3$
. The universal property of
![]() $A_{\operatorname{cris}}(\bar{R})$
gives a ring homomorphism
$A_{\operatorname{cris}}(\bar{R})$
gives a ring homomorphism
Using the crystalline description of Dieudonné displays of [Reference LauLa3], one obtains an
![]() $A_{\operatorname{cris}}(\bar{R})$
-linear map
$A_{\operatorname{cris}}(\bar{R})$
-linear map
compatible with Frobenius and filtration. We will show that
![]() $\unicode[STIX]{x1D70F}$
induces the identity on
$\unicode[STIX]{x1D70F}$
induces the identity on
![]() $T_{p}(G)$
, viewed as a submodule of
$T_{p}(G)$
, viewed as a submodule of
![]() $\operatorname{Fil}^{1}M_{\operatorname{cris}}$
by the period homomorphism and as a submodule of
$\operatorname{Fil}^{1}M_{\operatorname{cris}}$
by the period homomorphism and as a submodule of
![]() $\hat{Q}_{\tilde{R}}\subseteq \hat{P}_{\tilde{R}}$
by Theorem A; see Proposition 6.2.
$\hat{Q}_{\tilde{R}}\subseteq \hat{P}_{\tilde{R}}$
by Theorem A; see Proposition 6.2.
Relation with Breuil–Kisin modules
Let
![]() $\unicode[STIX]{x1D70B}\in R$
generate the maximal ideal. Let
$\unicode[STIX]{x1D70B}\in R$
generate the maximal ideal. Let
![]() $\mathfrak{S}=W(k)[[t]]$
and let
$\mathfrak{S}=W(k)[[t]]$
and let
![]() $\unicode[STIX]{x1D70E}:\mathfrak{S}\rightarrow \mathfrak{S}$
extend the Frobenius automorphism of
$\unicode[STIX]{x1D70E}:\mathfrak{S}\rightarrow \mathfrak{S}$
extend the Frobenius automorphism of
![]() $W(k)$
by
$W(k)$
by
![]() $t\mapsto t^{p}$
; see below for the case of more general Frobenius lifts. We consider pairs
$t\mapsto t^{p}$
; see below for the case of more general Frobenius lifts. We consider pairs
![]() $M=(M,\unicode[STIX]{x1D719})$
where
$M=(M,\unicode[STIX]{x1D719})$
where
![]() $M$
is an
$M$
is an
![]() $\mathfrak{S}$
-module of finite type and where
$\mathfrak{S}$
-module of finite type and where
![]() $\unicode[STIX]{x1D719}:M\rightarrow M^{(\unicode[STIX]{x1D70E})}=\mathfrak{S}\otimes _{\unicode[STIX]{x1D70E},\mathfrak{S}}M$
is an
$\unicode[STIX]{x1D719}:M\rightarrow M^{(\unicode[STIX]{x1D70E})}=\mathfrak{S}\otimes _{\unicode[STIX]{x1D70E},\mathfrak{S}}M$
is an
![]() $\mathfrak{S}$
-linear map with cokernel annihilated by the minimal polynomial of
$\mathfrak{S}$
-linear map with cokernel annihilated by the minimal polynomial of
![]() $\unicode[STIX]{x1D70B}$
over
$\unicode[STIX]{x1D70B}$
over
![]() $W(k)$
. Following [Reference Vasiu and ZinkVZ],
$W(k)$
. Following [Reference Vasiu and ZinkVZ],
![]() $M$
is called a Breuil window if
$M$
is called a Breuil window if
![]() $M$
is free over
$M$
is free over
![]() $\mathfrak{S}$
, and
$\mathfrak{S}$
, and
![]() $M$
is called a Breuil module if
$M$
is called a Breuil module if
![]() $M$
is a
$M$
is a
![]() $p$
-power torsion
$p$
-power torsion
![]() $\mathfrak{S}$
-module of projective dimension at most one. These notions are dual to the classical Breuil–Kisin modules.
$\mathfrak{S}$
-module of projective dimension at most one. These notions are dual to the classical Breuil–Kisin modules.
It is known that
![]() $p$
-divisible groups over
$p$
-divisible groups over
![]() $R$
are equivalent to Breuil windows. This was conjectured by Breuil [Reference BreuilBr] and proved by Kisin [Reference KisinKi1, Reference KisinKi2] if
$R$
are equivalent to Breuil windows. This was conjectured by Breuil [Reference BreuilBr] and proved by Kisin [Reference KisinKi1, Reference KisinKi2] if
![]() $p\geqslant 3$
, and for connected groups if
$p\geqslant 3$
, and for connected groups if
![]() $p=2$
. The general case is proved in [Reference LauLa3] by showing that Breuil windows are equivalent to Dieudonné displays. (This equivalence holds when
$p=2$
. The general case is proved in [Reference LauLa3] by showing that Breuil windows are equivalent to Dieudonné displays. (This equivalence holds when
![]() $R$
is regular of arbitrary dimension, with appropriate definition of
$R$
is regular of arbitrary dimension, with appropriate definition of
![]() $\mathfrak{S}$
. For
$\mathfrak{S}$
. For
![]() $p\geqslant 3$
this equivalence is already proved in [Reference Vasiu and ZinkVZ] for some regular rings, including all discrete valuation rings.) As a corollary, commutative finite flat
$p\geqslant 3$
this equivalence is already proved in [Reference Vasiu and ZinkVZ] for some regular rings, including all discrete valuation rings.) As a corollary, commutative finite flat
![]() $p$
-group schemes over
$p$
-group schemes over
![]() $R$
are equivalent to Breuil modules. Other proofs for
$R$
are equivalent to Breuil modules. Other proofs for
![]() $p=2$
, more closely related to Kisin’s methods, were obtained independently by Kim [Reference KimK] and Liu [Reference LiuLi].
$p=2$
, more closely related to Kisin’s methods, were obtained independently by Kim [Reference KimK] and Liu [Reference LiuLi].
Let
![]() $K_{\infty }$
be the extension of
$K_{\infty }$
be the extension of
![]() $K$
generated by a chosen system of successive
$K$
generated by a chosen system of successive
![]() $p$
th roots of
$p$
th roots of
![]() $\unicode[STIX]{x1D70B}$
. For a
$\unicode[STIX]{x1D70B}$
. For a
![]() $p$
-divisible group
$p$
-divisible group
![]() $G$
over
$G$
over
![]() $R$
let
$R$
let
![]() $T(G)$
be its Tate module, and for a commutative finite flat
$T(G)$
be its Tate module, and for a commutative finite flat
![]() $p$
-group scheme
$p$
-group scheme
![]() $G$
over
$G$
over
![]() $R$
let
$R$
let
![]() $T(G)=G(\bar{K})$
. The results of Kisin, Liu, and Kim include a description of
$T(G)=G(\bar{K})$
. The results of Kisin, Liu, and Kim include a description of
![]() $T(G)$
as a
$T(G)$
as a
![]() ${\mathcal{G}}_{K_{\infty }}$
-module in terms of the Breuil window or module
${\mathcal{G}}_{K_{\infty }}$
-module in terms of the Breuil window or module
![]() $(M,\unicode[STIX]{x1D719})$
corresponding to
$(M,\unicode[STIX]{x1D719})$
corresponding to
![]() $G$
. In the covariant theory used here it takes the form of an isomorphism of
$G$
. In the covariant theory used here it takes the form of an isomorphism of
![]() ${\mathcal{G}}_{K_{\infty }}$
-modules
${\mathcal{G}}_{K_{\infty }}$
-modules
![]() $T(G)\cong T^{\operatorname{nr}}(M)$
where
$T(G)\cong T^{\operatorname{nr}}(M)$
where
with
![]() $M^{\operatorname{nr}}=\mathfrak{S}^{\operatorname{nr}}\otimes _{\mathfrak{S}}M$
; the ring
$M^{\operatorname{nr}}=\mathfrak{S}^{\operatorname{nr}}\otimes _{\mathfrak{S}}M$
; the ring
![]() $\mathfrak{S}^{\operatorname{nr}}$
is recalled in Section 7.
$\mathfrak{S}^{\operatorname{nr}}$
is recalled in Section 7.
To complete the approach via Dieudonné displays, we will show how the isomorphism
![]() $T(G)\cong T^{\operatorname{nr}}(M)$
can be deduced from Theorem A; see Corollary 8.6. It suffices to consider the case where
$T(G)\cong T^{\operatorname{nr}}(M)$
can be deduced from Theorem A; see Corollary 8.6. It suffices to consider the case where
![]() $G$
is a
$G$
is a
![]() $p$
-divisible group. The equivalence between Breuil windows and Dieudonné displays over
$p$
-divisible group. The equivalence between Breuil windows and Dieudonné displays over
![]() $R$
is induced by a ring homomorphism
$R$
is induced by a ring homomorphism
![]() $\unicode[STIX]{x1D718}:\mathfrak{S}\rightarrow \mathbb{W}(R)$
, which extends to a ring homomorphism
$\unicode[STIX]{x1D718}:\mathfrak{S}\rightarrow \mathbb{W}(R)$
, which extends to a ring homomorphism
![]() $\unicode[STIX]{x1D718}^{\operatorname{nr}}:\mathfrak{S}^{\operatorname{nr}}\rightarrow \hat{\mathbb{W}}(\tilde{R}).$
Using Theorem A, this allows to define a homomorphism of
$\unicode[STIX]{x1D718}^{\operatorname{nr}}:\mathfrak{S}^{\operatorname{nr}}\rightarrow \hat{\mathbb{W}}(\tilde{R}).$
Using Theorem A, this allows to define a homomorphism of
![]() ${\mathcal{G}}_{K_{\infty }}$
-modules
${\mathcal{G}}_{K_{\infty }}$
-modules
and we show in Proposition 8.5 that
![]() $\unicode[STIX]{x1D70F}$
is bijective. The verification is easy if
$\unicode[STIX]{x1D70F}$
is bijective. The verification is easy if
![]() $G$
is étale, and the general case follows quite formally using a duality argument.
$G$
is étale, and the general case follows quite formally using a duality argument.
Other lifts of Frobenius
The equivalence between Breuil windows and
![]() $p$
-divisible groups requires only a Frobenius lift
$p$
-divisible groups requires only a Frobenius lift
![]() $\unicode[STIX]{x1D70E}:\mathfrak{S}\rightarrow \mathfrak{S}$
which stabilizes the ideal
$\unicode[STIX]{x1D70E}:\mathfrak{S}\rightarrow \mathfrak{S}$
which stabilizes the ideal
![]() $t\mathfrak{S}$
such that
$t\mathfrak{S}$
such that
![]() $p^{2}$
divides the linear term of the power series
$p^{2}$
divides the linear term of the power series
![]() $\unicode[STIX]{x1D70E}(t)$
. In this case, let
$\unicode[STIX]{x1D70E}(t)$
. In this case, let
![]() $K_{\infty }$
be the extension of
$K_{\infty }$
be the extension of
![]() $K$
generated by a system
$K$
generated by a system
![]() $\unicode[STIX]{x1D70B}^{(n)}\in \bar{K}$
of successive
$\unicode[STIX]{x1D70B}^{(n)}\in \bar{K}$
of successive
![]() $\unicode[STIX]{x1D70E}(t)$
-roots of
$\unicode[STIX]{x1D70E}(t)$
-roots of
![]() $\unicode[STIX]{x1D70B}$
, which means that
$\unicode[STIX]{x1D70B}$
, which means that
![]() $\unicode[STIX]{x1D70B}^{(0)}=\unicode[STIX]{x1D70B}$
and
$\unicode[STIX]{x1D70B}^{(0)}=\unicode[STIX]{x1D70B}$
and
![]() $\unicode[STIX]{x1D70E}(t)(\unicode[STIX]{x1D70B}^{(n+1)})=\unicode[STIX]{x1D70B}^{(n)}$
. Then we obtain an isomorphism of
$\unicode[STIX]{x1D70E}(t)(\unicode[STIX]{x1D70B}^{(n+1)})=\unicode[STIX]{x1D70B}^{(n)}$
. Then we obtain an isomorphism of
![]() ${\mathcal{G}}_{K_{\infty }}$
-modules
${\mathcal{G}}_{K_{\infty }}$
-modules
![]() $T(G)\cong T^{\operatorname{nr}}(M)$
as before; here the ring
$T(G)\cong T^{\operatorname{nr}}(M)$
as before; here the ring
![]() $\mathfrak{S}^{\operatorname{nr}}$
depends on
$\mathfrak{S}^{\operatorname{nr}}$
depends on
![]() $\unicode[STIX]{x1D70E}$
as well.
$\unicode[STIX]{x1D70E}$
as well.
1 Notation
All rings are commutative and unitary unless the contrary is stated. For the convenience of the reader we recall the notion of frames, windows, and displays.
A frame
![]() $\mathscr{F}=(S,I,R,\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70E}_{1})$
in the sense of [Reference LauLa2] consists of a pair of rings
$\mathscr{F}=(S,I,R,\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70E}_{1})$
in the sense of [Reference LauLa2] consists of a pair of rings
![]() $S$
and
$S$
and
![]() $R=S/I$
with
$R=S/I$
with
![]() $I+pS\subseteq \operatorname{Rad}(S)$
, a ring endomorphism
$I+pS\subseteq \operatorname{Rad}(S)$
, a ring endomorphism
![]() $\unicode[STIX]{x1D70E}:S\rightarrow S$
that lifts the Frobenius of
$\unicode[STIX]{x1D70E}:S\rightarrow S$
that lifts the Frobenius of
![]() $S/pS$
, and a
$S/pS$
, and a
![]() $\unicode[STIX]{x1D70E}$
-linear map
$\unicode[STIX]{x1D70E}$
-linear map
![]() $\unicode[STIX]{x1D70E}_{1}:I\rightarrow S$
with
$\unicode[STIX]{x1D70E}_{1}:I\rightarrow S$
with
![]() $\unicode[STIX]{x1D70E}_{1}(I)S=S$
.
$\unicode[STIX]{x1D70E}_{1}(I)S=S$
.
We assume that
![]() $S$
is a local ring. Then an
$S$
is a local ring. Then an
![]() $\mathscr{F}$
-window
$\mathscr{F}$
-window
![]() $\mathscr{P}=(P,Q,F,F_{1})$
consists of a finite free
$\mathscr{P}=(P,Q,F,F_{1})$
consists of a finite free
![]() $S$
-module
$S$
-module
![]() $P$
, a submodule
$P$
, a submodule
![]() $Q\subseteq P$
with
$Q\subseteq P$
with
![]() $IP\subseteq Q$
such that
$IP\subseteq Q$
such that
![]() $P/Q$
is free over
$P/Q$
is free over
![]() $R$
, and a pair of
$R$
, and a pair of
![]() $\unicode[STIX]{x1D70E}$
-linear maps
$\unicode[STIX]{x1D70E}$
-linear maps
![]() $F:P\rightarrow P$
and
$F:P\rightarrow P$
and
![]() $F_{1}:Q\rightarrow P$
with
$F_{1}:Q\rightarrow P$
with
![]() $F_{1}(ax)=\unicode[STIX]{x1D70E}_{1}(a)F(x)$
for
$F_{1}(ax)=\unicode[STIX]{x1D70E}_{1}(a)F(x)$
for
![]() $a\in I$
and
$a\in I$
and
![]() $x\in P$
, such that
$x\in P$
, such that
![]() $F_{1}(Q)$
generates
$F_{1}(Q)$
generates
![]() $P$
. Then there is a unique
$P$
. Then there is a unique
![]() $S$
-linear map
$S$
-linear map
![]() $V^{\sharp }:P\rightarrow S\otimes _{\unicode[STIX]{x1D70E},S}P=P^{(\unicode[STIX]{x1D70E})}$
with
$V^{\sharp }:P\rightarrow S\otimes _{\unicode[STIX]{x1D70E},S}P=P^{(\unicode[STIX]{x1D70E})}$
with
![]() $V^{\sharp }(F_{1}(x))=1\otimes x$
for
$V^{\sharp }(F_{1}(x))=1\otimes x$
for
![]() $x\in Q$
. A sequence
$x\in Q$
. A sequence
![]() $0\rightarrow \mathscr{P}\rightarrow \mathscr{P}^{\prime }\rightarrow \mathscr{P}^{\prime \prime }\rightarrow 0$
of
$0\rightarrow \mathscr{P}\rightarrow \mathscr{P}^{\prime }\rightarrow \mathscr{P}^{\prime \prime }\rightarrow 0$
of
![]() $\mathscr{F}$
-windows will be called exact if the resulting sequences of
$\mathscr{F}$
-windows will be called exact if the resulting sequences of
![]() $P$
’s and of
$P$
’s and of
![]() $Q$
’s are exact.
$Q$
’s are exact.
A frame homomorphism
![]() $\unicode[STIX]{x1D6FC}:\mathscr{F}\rightarrow \mathscr{F}^{\prime }=(S^{\prime },I^{\prime },R^{\prime },\unicode[STIX]{x1D70E}^{\prime },\unicode[STIX]{x1D70E}_{1}^{\prime })$
is a ring homomorphism
$\unicode[STIX]{x1D6FC}:\mathscr{F}\rightarrow \mathscr{F}^{\prime }=(S^{\prime },I^{\prime },R^{\prime },\unicode[STIX]{x1D70E}^{\prime },\unicode[STIX]{x1D70E}_{1}^{\prime })$
is a ring homomorphism
![]() $\unicode[STIX]{x1D6FC}:S\rightarrow S^{\prime }$
with
$\unicode[STIX]{x1D6FC}:S\rightarrow S^{\prime }$
with
![]() $\unicode[STIX]{x1D6FC}(I)\subseteq I^{\prime }$
such that
$\unicode[STIX]{x1D6FC}(I)\subseteq I^{\prime }$
such that
![]() $\unicode[STIX]{x1D70E}^{\prime }\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D70E}$
and
$\unicode[STIX]{x1D70E}^{\prime }\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FC}\unicode[STIX]{x1D70E}$
and
![]() $\unicode[STIX]{x1D70E}_{1}^{\prime }\unicode[STIX]{x1D6FC}=u\cdot \unicode[STIX]{x1D6FC}\unicode[STIX]{x1D70E}_{1}$
for a unit
$\unicode[STIX]{x1D70E}_{1}^{\prime }\unicode[STIX]{x1D6FC}=u\cdot \unicode[STIX]{x1D6FC}\unicode[STIX]{x1D70E}_{1}$
for a unit
![]() $u\in S^{\prime }$
, which then is unique. If
$u\in S^{\prime }$
, which then is unique. If
![]() $u=1$
then
$u=1$
then
![]() $\unicode[STIX]{x1D6FC}$
is called strict. There is a base change functor
$\unicode[STIX]{x1D6FC}$
is called strict. There is a base change functor
where
![]() $\unicode[STIX]{x1D6FC}_{\ast }(\mathscr{P})=(P^{\prime },Q^{\prime },F^{\prime },F_{1}^{\prime })$
is determined by
$\unicode[STIX]{x1D6FC}_{\ast }(\mathscr{P})=(P^{\prime },Q^{\prime },F^{\prime },F_{1}^{\prime })$
is determined by
![]() $P^{\prime }=S^{\prime }\otimes _{S}P$
and
$P^{\prime }=S^{\prime }\otimes _{S}P$
and
![]() $P^{\prime }/Q^{\prime }=(P/Q)\otimes _{R}R^{\prime }$
with
$P^{\prime }/Q^{\prime }=(P/Q)\otimes _{R}R^{\prime }$
with
![]() $F^{\prime }(1\otimes x)=1\otimes F(x)$
for
$F^{\prime }(1\otimes x)=1\otimes F(x)$
for
![]() $x\in P$
and
$x\in P$
and
![]() $F_{1}^{\prime }(1\otimes x)=u\otimes F_{1}(x)$
for
$F_{1}^{\prime }(1\otimes x)=u\otimes F_{1}(x)$
for
![]() $x\in Q$
.
$x\in Q$
.
For a not necessarily unitary ring
![]() $R$
let
$R$
let
![]() $W(R)$
be the ring of
$W(R)$
be the ring of
![]() $p$
-typical Witt vectors. If
$p$
-typical Witt vectors. If
![]() $R$
is
$R$
is
![]() $p$
-adic and unitary, we have a frame
$p$
-adic and unitary, we have a frame
where
![]() $I_{R}$
is the image of the Verschiebung
$I_{R}$
is the image of the Verschiebung
![]() $v:W(R)\rightarrow W(R)$
, where
$v:W(R)\rightarrow W(R)$
, where
![]() $f$
is the Frobenius, and
$f$
is the Frobenius, and
![]() $f_{1}$
is the inverse of
$f_{1}$
is the inverse of
![]() $v$
. Windows over
$v$
. Windows over
![]() $\mathscr{W}(R)$
are the displays over
$\mathscr{W}(R)$
are the displays over
![]() $R$
of [Reference ZinkZi1]. A display is called
$R$
of [Reference ZinkZi1]. A display is called
![]() $V$
-nilpotent if the map
$V$
-nilpotent if the map
![]() $V^{\sharp }$
becomes nilpotent over
$V^{\sharp }$
becomes nilpotent over
![]() $R/pR$
. A homomorphism
$R/pR$
. A homomorphism
![]() $R\rightarrow R^{\prime }$
gives a strict frame homomorphism
$R\rightarrow R^{\prime }$
gives a strict frame homomorphism
![]() $\mathscr{W}(R)\rightarrow \mathscr{W}(R^{\prime })$
, and we write
$\mathscr{W}(R)\rightarrow \mathscr{W}(R^{\prime })$
, and we write
![]() $\mathscr{P}\mapsto \mathscr{P}\otimes _{R}R^{\prime }$
for the resulting base change of displays.
$\mathscr{P}\mapsto \mathscr{P}\otimes _{R}R^{\prime }$
for the resulting base change of displays.
If
![]() $N$
is a nilpotent nonunitary ring,
$N$
is a nilpotent nonunitary ring,
![]() ${\hat{W}}(N)\subseteq W(N)$
denotes the subgroup of all Witt vectors with only finitely many nonzero coefficients. If
${\hat{W}}(N)\subseteq W(N)$
denotes the subgroup of all Witt vectors with only finitely many nonzero coefficients. If
![]() $A$
is a local Artin ring with perfect residue field
$A$
is a local Artin ring with perfect residue field
![]() $k=A/\mathfrak{m}$
of characteristic
$k=A/\mathfrak{m}$
of characteristic
![]() $p$
, there is a unique ring homomorphism
$p$
, there is a unique ring homomorphism
![]() $s:W(k)\rightarrow W(A)$
that lifts the projection
$s:W(k)\rightarrow W(A)$
that lifts the projection
![]() $W(A)\rightarrow W(k)$
, and the Zink ring
$W(A)\rightarrow W(k)$
, and the Zink ring
![]() $\mathbb{W}(A)={\hat{W}}(\mathfrak{m})\oplus s(W(k))$
is a subring of
$\mathbb{W}(A)={\hat{W}}(\mathfrak{m})\oplus s(W(k))$
is a subring of
![]() $W(A)$
. There is a frame
$W(A)$
. There is a frame
![]() $\mathscr{D}_{A}=(\mathbb{W}(A),\mathbb{I}(A),A,f,f_{1})$
with an injective frame homomorphism
$\mathscr{D}_{A}=(\mathbb{W}(A),\mathbb{I}(A),A,f,f_{1})$
with an injective frame homomorphism
![]() $\mathscr{D}_{A}\rightarrow \mathscr{W}_{A}$
, which is strict when
$\mathscr{D}_{A}\rightarrow \mathscr{W}_{A}$
, which is strict when
![]() $p\geqslant 3$
; see [Reference LauLa3, Section 2.C]. Windows over
$p\geqslant 3$
; see [Reference LauLa3, Section 2.C]. Windows over
![]() $\mathscr{D}_{A}$
are called Dieudonné displays over
$\mathscr{D}_{A}$
are called Dieudonné displays over
![]() $A$
.
$A$
.
2 The case of connected
 $p$
-divisible groups
$p$
-divisible groups
Let
![]() $R$
be a normal complete noetherian local ring with (not necessarily perfect) residue field
$R$
be a normal complete noetherian local ring with (not necessarily perfect) residue field
![]() $k$
of positive characteristic
$k$
of positive characteristic
![]() $p$
, with fraction field
$p$
, with fraction field
![]() $K$
of characteristic zero, and with maximal ideal
$K$
of characteristic zero, and with maximal ideal
![]() $\mathfrak{m}$
. In this section, we recall how the Tate module of a connected
$\mathfrak{m}$
. In this section, we recall how the Tate module of a connected
![]() $p$
-divisible group over
$p$
-divisible group over
![]() $R$
is expressed in terms of its nilpotent display.
$R$
is expressed in terms of its nilpotent display.
We fix an algebraic closure
![]() $\bar{K}$
of
$\bar{K}$
of
![]() $K$
and write
$K$
and write
![]() ${\mathcal{G}}_{K}=\operatorname{Gal}(\bar{K}/K)$
. Let
${\mathcal{G}}_{K}=\operatorname{Gal}(\bar{K}/K)$
. Let
![]() $\bar{R}\subset \bar{K}$
be the integral closure of
$\bar{R}\subset \bar{K}$
be the integral closure of
![]() $R$
, and for a finite extension
$R$
, and for a finite extension
![]() $E/K$
in
$E/K$
in
![]() $\bar{K}$
let
$\bar{K}$
let
![]() $R_{E}=\bar{R}\cap E$
. Then
$R_{E}=\bar{R}\cap E$
. Then
![]() $R_{E}$
is finite over
$R_{E}$
is finite over
![]() $R$
, and
$R$
, and
![]() $R_{E}$
is a complete noetherian local ring. Thus
$R_{E}$
is a complete noetherian local ring. Thus
![]() $\bar{R}$
is a local ring. Let
$\bar{R}$
is a local ring. Let
![]() $\bar{\mathfrak{m}}\subset \bar{R}$
and
$\bar{\mathfrak{m}}\subset \bar{R}$
and
![]() $\mathfrak{m}_{E}\subset R_{E}$
be the maximal ideals. We write
$\mathfrak{m}_{E}\subset R_{E}$
be the maximal ideals. We write
Let
![]() $\bar{W}(\bar{\mathfrak{m}})$
be the
$\bar{W}(\bar{\mathfrak{m}})$
be the
![]() $p$
-adic completion of
$p$
-adic completion of
![]() ${\hat{W}}(\bar{\mathfrak{m}})$
and let
${\hat{W}}(\bar{\mathfrak{m}})$
and let
![]() $\bar{\mathfrak{m}}^{\wedge }$
be the
$\bar{\mathfrak{m}}^{\wedge }$
be the
![]() $p$
-adic completion of
$p$
-adic completion of
![]() $\bar{\mathfrak{m}}$
. The natural map
$\bar{\mathfrak{m}}$
. The natural map
![]() $\bar{W}(\bar{\mathfrak{m}})\rightarrow \bar{\mathfrak{m}}^{\wedge }$
is surjective. For a display
$\bar{W}(\bar{\mathfrak{m}})\rightarrow \bar{\mathfrak{m}}^{\wedge }$
is surjective. For a display
![]() $\mathscr{P}=(P,Q,F,F_{1})$
over
$\mathscr{P}=(P,Q,F,F_{1})$
over
![]() $R$
let
$R$
let
We call
![]() $\mathscr{P}$
nilpotent if the reduction
$\mathscr{P}$
nilpotent if the reduction
![]() $\mathscr{P}\otimes _{R}k$
is
$\mathscr{P}\otimes _{R}k$
is
![]() $V$
-nilpotent in the usual sense, or equivalently if
$V$
-nilpotent in the usual sense, or equivalently if
![]() $\mathscr{P}\otimes _{R}R/\mathfrak{m}_{R}^{n}$
is
$\mathscr{P}\otimes _{R}R/\mathfrak{m}_{R}^{n}$
is
![]() $V$
-nilpotent for all
$V$
-nilpotent for all
![]() $n$
; cf. [Reference ZinkZi1, Definition 13]. The functor
$n$
; cf. [Reference ZinkZi1, Definition 13]. The functor
![]() $\operatorname{BT}$
of [Reference ZinkZi1] induces an equivalence of categories between nilpotent displays over
$\operatorname{BT}$
of [Reference ZinkZi1] induces an equivalence of categories between nilpotent displays over
![]() $R$
and connected
$R$
and connected
![]() $p$
-divisible groups over
$p$
-divisible groups over
![]() $R$
; this follows from [Reference ZinkZi1, Theorem 9] applied to the rings
$R$
; this follows from [Reference ZinkZi1, Theorem 9] applied to the rings
![]() $R/\mathfrak{m}_{R}^{n}$
, using that
$R/\mathfrak{m}_{R}^{n}$
, using that
![]() $V$
-nilpotent displays and
$V$
-nilpotent displays and
![]() $p$
-divisible groups over
$p$
-divisible groups over
![]() $R$
are equivalent to compatible systems of such objects over
$R$
are equivalent to compatible systems of such objects over
![]() $R/\mathfrak{m}_{R}^{n}$
for all
$R/\mathfrak{m}_{R}^{n}$
for all
![]() $n$
. A variant of the following result is stated in [Reference MessingMe2, Proposition 4.4].
$n$
. A variant of the following result is stated in [Reference MessingMe2, Proposition 4.4].
Proposition 2.1. (Zink)
Let
![]() $\mathscr{P}$
be a nilpotent display over
$\mathscr{P}$
be a nilpotent display over
![]() $R$
and let
$R$
and let
![]() $G=\operatorname{BT}(\mathscr{P})$
be the associated connected
$G=\operatorname{BT}(\mathscr{P})$
be the associated connected
![]() $p$
-divisible group over
$p$
-divisible group over
![]() $R$
. There is a natural exact sequence of
$R$
. There is a natural exact sequence of
![]() ${\mathcal{G}}_{K}$
-modules
${\mathcal{G}}_{K}$
-modules
Here
![]() $T_{p}(G)=\operatorname{Hom}(\mathbb{Q}_{p}/\mathbb{Z}_{p},G(\bar{K}))$
is the Tate module of
$T_{p}(G)=\operatorname{Hom}(\mathbb{Q}_{p}/\mathbb{Z}_{p},G(\bar{K}))$
is the Tate module of
![]() $G$
, and
$G$
, and
![]() ${\mathcal{G}}_{K}$
acts on
${\mathcal{G}}_{K}$
acts on
![]() $\bar{P}_{\bar{\mathfrak{m}}}$
and
$\bar{P}_{\bar{\mathfrak{m}}}$
and
![]() $\bar{Q}_{\bar{\mathfrak{m}}}$
by its natural action on
$\bar{Q}_{\bar{\mathfrak{m}}}$
by its natural action on
![]() $\bar{W}(\bar{\mathfrak{m}})$
.
$\bar{W}(\bar{\mathfrak{m}})$
.
The proof of Proposition 2.1 uses the following standard facts.
Lemma 2.2. Let
![]() $A$
be an abelian group.
$A$
be an abelian group.
(i) If
 $A$
has no
$A$
has no
 $p$
-torsion then
$p$
-torsion then
 $\operatorname{Ext}^{1}(\mathbb{Q}_{p}/\mathbb{Z}_{p},A)=\varprojlim A/p^{n}A$
.
$\operatorname{Ext}^{1}(\mathbb{Q}_{p}/\mathbb{Z}_{p},A)=\varprojlim A/p^{n}A$
.(ii) If
 $pA=A$
then
$pA=A$
then
 $\operatorname{Ext}^{1}(\mathbb{Q}_{p}/\mathbb{Z}_{p},A)$
is zero.
$\operatorname{Ext}^{1}(\mathbb{Q}_{p}/\mathbb{Z}_{p},A)$
is zero.
Proof. The group
![]() $\operatorname{Hom}(\mathbb{Q}_{p}/\mathbb{Z}_{p},A)$
is isomorphic to
$\operatorname{Hom}(\mathbb{Q}_{p}/\mathbb{Z}_{p},A)$
is isomorphic to
![]() $\varprojlim \operatorname{Hom}(\mathbb{Z}/p^{n}\mathbb{Z},A)$
with transition maps induced by
$\varprojlim \operatorname{Hom}(\mathbb{Z}/p^{n}\mathbb{Z},A)$
with transition maps induced by
![]() $p:\mathbb{Z}/p^{n}\mathbb{Z}\rightarrow \mathbb{Z}/p^{n+1}\mathbb{Z}$
. If the abelian group
$p:\mathbb{Z}/p^{n}\mathbb{Z}\rightarrow \mathbb{Z}/p^{n+1}\mathbb{Z}$
. If the abelian group
![]() $A$
is injective, the projective system
$A$
is injective, the projective system
![]() $\operatorname{Hom}(\mathbb{Z}/p^{n}\mathbb{Z},A)$
has surjective transition maps and thus its
$\operatorname{Hom}(\mathbb{Z}/p^{n}\mathbb{Z},A)$
has surjective transition maps and thus its
![]() $\varprojlim ^{1}$
vanishes. Hence there is a Grothendieck spectral sequence for the functor
$\varprojlim ^{1}$
vanishes. Hence there is a Grothendieck spectral sequence for the functor
![]() $A\mapsto \operatorname{Hom}(\mathbb{Z}/p^{n},A)_{n}$
from abelian groups to projective systems of abelian groups, composed with the functor
$A\mapsto \operatorname{Hom}(\mathbb{Z}/p^{n},A)_{n}$
from abelian groups to projective systems of abelian groups, composed with the functor
![]() $\varprojlim$
,
$\varprojlim$
,
The projective system of groups
![]() $\operatorname{Ext}^{1}(\mathbb{Z}/p^{n}\mathbb{Z},A)$
is isomorphic to the system
$\operatorname{Ext}^{1}(\mathbb{Z}/p^{n}\mathbb{Z},A)$
is isomorphic to the system
![]() $A/p^{n}A$
with transition maps induced by
$A/p^{n}A$
with transition maps induced by
![]() $\operatorname{id}_{A}$
. Thus the exact sequence of low degree terms (see for example, [Reference WeibelWe, Theorem 5.8.3]) associated to (2.1) gives an exact sequence
$\operatorname{id}_{A}$
. Thus the exact sequence of low degree terms (see for example, [Reference WeibelWe, Theorem 5.8.3]) associated to (2.1) gives an exact sequence
If
![]() $A$
has no
$A$
has no
![]() $p$
-torsion then
$p$
-torsion then
![]() $\operatorname{Hom}(\mathbb{Z}/p^{n}\mathbb{Z},A)=0$
, and (i) follows. If
$\operatorname{Hom}(\mathbb{Z}/p^{n}\mathbb{Z},A)=0$
, and (i) follows. If
![]() $pA=A$
then the projective system
$pA=A$
then the projective system
![]() $\operatorname{Hom}(\mathbb{Z}/p^{n}\mathbb{Z},A)$
has surjective transition maps, thus its
$\operatorname{Hom}(\mathbb{Z}/p^{n}\mathbb{Z},A)$
has surjective transition maps, thus its
![]() $\varprojlim ^{1}$
is zero, moreover
$\varprojlim ^{1}$
is zero, moreover
![]() $A/p^{n}A=0$
. This proves (ii).◻
$A/p^{n}A=0$
. This proves (ii).◻
For a
![]() $p$
-divisible group
$p$
-divisible group
![]() $G$
over
$G$
over
![]() $R$
and for
$R$
and for
![]() $E$
as above we write
$E$
as above we write
Lemma 2.3. Multiplication by
![]() $p$
is surjective on
$p$
is surjective on
![]() ${\hat{G}}(\bar{R})$
.
${\hat{G}}(\bar{R})$
.
Proof. Let
![]() $x\in {\hat{G}}(R_{E})$
be given. The inverse image of
$x\in {\hat{G}}(R_{E})$
be given. The inverse image of
![]() $x$
under the multiplication map
$x$
under the multiplication map
![]() $p:G\rightarrow G$
is a compatible system of
$p:G\rightarrow G$
is a compatible system of
![]() $G[p]$
-torsors
$G[p]$
-torsors
![]() $Y_{n}$
over
$Y_{n}$
over
![]() $R_{E}/\mathfrak{m}_{E}^{n}$
. Let
$R_{E}/\mathfrak{m}_{E}^{n}$
. Let
![]() $Y_{n}=\operatorname{Spec}A_{n}$
and
$Y_{n}=\operatorname{Spec}A_{n}$
and
![]() $A=\varprojlim A_{n}$
. Then
$A=\varprojlim A_{n}$
. Then
![]() $Y=\operatorname{Spec}A$
is a
$Y=\operatorname{Spec}A$
is a
![]() $G[p]$
-torsor over
$G[p]$
-torsor over
![]() $R_{E}$
. For some finite extension
$R_{E}$
. For some finite extension
![]() $F$
of
$F$
of
![]() $E$
the set
$E$
the set
![]() $Y(F)=Y(R_{F})$
is nonempty, and
$Y(F)=Y(R_{F})$
is nonempty, and
![]() $x$
becomes divisible by
$x$
becomes divisible by
![]() $p$
in
$p$
in
![]() ${\hat{G}}(R_{F})$
.◻
${\hat{G}}(R_{F})$
.◻
Lemma 2.4. There is an isomorphism
![]() $G(\bar{K})[p^{r}]\cong {\hat{G}}(\bar{R})[p^{r}]$
of
$G(\bar{K})[p^{r}]\cong {\hat{G}}(\bar{R})[p^{r}]$
of
![]() ${\mathcal{G}}_{K}$
-modules.
${\mathcal{G}}_{K}$
-modules.
Proof. Let
![]() $G_{r}=G[p^{r}]$
. Then
$G_{r}=G[p^{r}]$
. Then
![]() ${\hat{G}}(R_{E})[p^{r}]=\mathop{\varprojlim }\nolimits_{n}G_{r}(R_{E}/\mathfrak{m}_{E}^{n})\cong G_{r}(R_{E})$
since
${\hat{G}}(R_{E})[p^{r}]=\mathop{\varprojlim }\nolimits_{n}G_{r}(R_{E}/\mathfrak{m}_{E}^{n})\cong G_{r}(R_{E})$
since
![]() $R_{E}$
is complete. Hence
$R_{E}$
is complete. Hence
![]() ${\hat{G}}(\bar{R})[p^{r}]\cong G_{r}(\bar{R})=G_{r}(\bar{K})=G(\bar{K})[p^{r}]$
.◻
${\hat{G}}(\bar{R})[p^{r}]\cong G_{r}(\bar{R})=G_{r}(\bar{K})=G(\bar{K})[p^{r}]$
.◻
Proof of Proposition 2.1.
For a finite Galois extension
![]() $E/K$
in
$E/K$
in
![]() $\bar{K}$
we write
$\bar{K}$
we write
and define
![]() $\hat{Q}_{E,n}$
by the exact sequence of
$\hat{Q}_{E,n}$
by the exact sequence of
![]() ${\mathcal{G}}_{K}$
-modules
${\mathcal{G}}_{K}$
-modules
The definition of the functor
![]() $\operatorname{BT}$
in [Reference ZinkZi1, Theorem 81] gives an exact sequence of
$\operatorname{BT}$
in [Reference ZinkZi1, Theorem 81] gives an exact sequence of
![]() ${\mathcal{G}}_{K}$
-modules
${\mathcal{G}}_{K}$
-modules
note that in [Reference ZinkZi1] a formal group
![]() $G$
is viewed as a functor
$G$
is viewed as a functor
![]() $G^{\prime }$
on nilpotent algebras, and
$G^{\prime }$
on nilpotent algebras, and
![]() $G(R_{E}/\mathfrak{m}_{E}^{n})=G^{\prime }(\mathfrak{m}_{E}/\mathfrak{m}_{E}^{n})$
under this identification. The modules
$G(R_{E}/\mathfrak{m}_{E}^{n})=G^{\prime }(\mathfrak{m}_{E}/\mathfrak{m}_{E}^{n})$
under this identification. The modules
![]() $\hat{Q}_{E,n}$
form a projective system with respect to
$\hat{Q}_{E,n}$
form a projective system with respect to
![]() $n$
with surjective transition maps. Indeed, using a normal decomposition of
$n$
with surjective transition maps. Indeed, using a normal decomposition of
![]() $\mathscr{P}$
as in the paragraph before [Reference ZinkZi1, Theorem 81], this is reduced to the assertion that
$\mathscr{P}$
as in the paragraph before [Reference ZinkZi1, Theorem 81], this is reduced to the assertion that
![]() ${\hat{W}}(\mathfrak{m}_{E}/\mathfrak{m}_{E}^{n+1})\rightarrow {\hat{W}}(\mathfrak{m}_{E}/\mathfrak{m}_{E}^{n})$
is surjective, which is clear. Thus taking
${\hat{W}}(\mathfrak{m}_{E}/\mathfrak{m}_{E}^{n+1})\rightarrow {\hat{W}}(\mathfrak{m}_{E}/\mathfrak{m}_{E}^{n})$
is surjective, which is clear. Thus taking
![]() $\mathop{\varinjlim }\nolimits_{E}\mathop{\varprojlim }\nolimits_{n}$
of the preceding two sequences gives exact sequences of
$\mathop{\varinjlim }\nolimits_{E}\mathop{\varprojlim }\nolimits_{n}$
of the preceding two sequences gives exact sequences of
![]() ${\mathcal{G}}_{K}$
-modules
${\mathcal{G}}_{K}$
-modules
and
with
![]() $\hat{Q}_{\bar{\mathfrak{m}}}=\mathop{\varinjlim }\nolimits_{E}\mathop{\varprojlim }\nolimits_{n}\hat{Q}_{E,n}$
and
$\hat{Q}_{\bar{\mathfrak{m}}}=\mathop{\varinjlim }\nolimits_{E}\mathop{\varprojlim }\nolimits_{n}\hat{Q}_{E,n}$
and
![]() $\hat{P}_{\bar{\mathfrak{m}}}={\hat{W}}(\bar{\mathfrak{m}})\otimes _{W(R)}P$
. Since
$\hat{P}_{\bar{\mathfrak{m}}}={\hat{W}}(\bar{\mathfrak{m}})\otimes _{W(R)}P$
. Since
![]() $\bar{\mathfrak{m}}\otimes _{R}P/Q$
has no
$\bar{\mathfrak{m}}\otimes _{R}P/Q$
has no
![]() $p$
-torsion, the
$p$
-torsion, the
![]() $p$
-adic completion of (2.2) remains exact, moreover the
$p$
-adic completion of (2.2) remains exact, moreover the
![]() $p$
-adic completion of the second and third terms are
$p$
-adic completion of the second and third terms are
![]() $\bar{P}_{\bar{\mathfrak{m}}}$
and
$\bar{P}_{\bar{\mathfrak{m}}}$
and
![]() $\bar{\mathfrak{m}}^{\wedge }\otimes _{R}P/Q$
. Thus the
$\bar{\mathfrak{m}}^{\wedge }\otimes _{R}P/Q$
. Thus the
![]() $p$
-adic completion of
$p$
-adic completion of
![]() $\hat{Q}_{\bar{\mathfrak{m}}}$
is
$\hat{Q}_{\bar{\mathfrak{m}}}$
is
![]() $\bar{Q}_{\bar{\mathfrak{m}}}$
. Moreover
$\bar{Q}_{\bar{\mathfrak{m}}}$
. Moreover
![]() $\hat{P}_{\bar{\mathfrak{m}}}$
has no
$\hat{P}_{\bar{\mathfrak{m}}}$
has no
![]() $p$
-torsion since
$p$
-torsion since
![]() ${\hat{W}}(\bar{\mathfrak{m}})$
is contained in the
${\hat{W}}(\bar{\mathfrak{m}})$
is contained in the
![]() $\mathbb{Q}$
-algebra
$\mathbb{Q}$
-algebra
![]() $W(\bar{K})$
. Using Lemmas 2.3 and 2.2, the
$W(\bar{K})$
. Using Lemmas 2.3 and 2.2, the
![]() $\operatorname{Ext}$
-sequence of
$\operatorname{Ext}$
-sequence of
![]() $\mathbb{Q}_{p}/\mathbb{Z}_{p}$
with (2.3) reduces to the short exact sequence
$\mathbb{Q}_{p}/\mathbb{Z}_{p}$
with (2.3) reduces to the short exact sequence
Lemma 2.4 gives an isomorphism
![]() $\operatorname{Hom}(\mathbb{Q}_{p}/\mathbb{Z}_{p},{\hat{G}}(\bar{R}))\cong T_{p}(G)$
of
$\operatorname{Hom}(\mathbb{Q}_{p}/\mathbb{Z}_{p},{\hat{G}}(\bar{R}))\cong T_{p}(G)$
of
![]() ${\mathcal{G}}_{K}$
-modules.◻
${\mathcal{G}}_{K}$
-modules.◻
3 Module of invariants
Before we proceed we introduce a formal definition. Let
![]() $\mathscr{F}=(S,I,R,\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70E}_{1})$
be a frame in the sense of [Reference LauLa2] such that
$\mathscr{F}=(S,I,R,\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70E}_{1})$
be a frame in the sense of [Reference LauLa2] such that
![]() $S$
is a
$S$
is a
![]() $\mathbb{Z}_{p}$
-algebra and
$\mathbb{Z}_{p}$
-algebra and
![]() $\unicode[STIX]{x1D70E}$
is
$\unicode[STIX]{x1D70E}$
is
![]() $\mathbb{Z}_{p}$
-linear; see Section 1. For an
$\mathbb{Z}_{p}$
-linear; see Section 1. For an
![]() $\mathscr{F}$
-window
$\mathscr{F}$
-window
![]() $\mathscr{P}=(P,Q,F,F_{1})$
we consider the module of invariants
$\mathscr{P}=(P,Q,F,F_{1})$
we consider the module of invariants
this is a
![]() $\mathbb{Z}_{p}$
-module. Let us record some of its formal properties.
$\mathbb{Z}_{p}$
-module. Let us record some of its formal properties.
Functoriality in
 $\mathscr{F}$
$\mathscr{F}$
Let
![]() $\unicode[STIX]{x1D6FC}:\mathscr{F}\rightarrow \mathscr{F}^{\prime }=(S^{\prime },I^{\prime },R^{\prime },\unicode[STIX]{x1D70E}^{\prime },\unicode[STIX]{x1D70E}_{1}^{\prime })$
be a
$\unicode[STIX]{x1D6FC}:\mathscr{F}\rightarrow \mathscr{F}^{\prime }=(S^{\prime },I^{\prime },R^{\prime },\unicode[STIX]{x1D70E}^{\prime },\unicode[STIX]{x1D70E}_{1}^{\prime })$
be a
![]() $u$
-homomorphism of frames; see Section 1. Assume that a unit
$u$
-homomorphism of frames; see Section 1. Assume that a unit
![]() $c\in S^{\prime }$
with
$c\in S^{\prime }$
with
![]() $c\unicode[STIX]{x1D70E}^{\prime }(c)^{-1}=u$
is given. For an
$c\unicode[STIX]{x1D70E}^{\prime }(c)^{-1}=u$
is given. For an
![]() $\mathscr{F}$
-window
$\mathscr{F}$
-window
![]() $\mathscr{P}$
as above, one verifies that the
$\mathscr{P}$
as above, one verifies that the
![]() $S$
-linear map
$S$
-linear map
![]() $P\rightarrow S^{\prime }\otimes _{S}P$
,
$P\rightarrow S^{\prime }\otimes _{S}P$
,
![]() $x\mapsto c\otimes x$
induces a
$x\mapsto c\otimes x$
induces a
![]() $\mathbb{Z}_{p}$
-linear map
$\mathbb{Z}_{p}$
-linear map
Duality
A bilinear form of
![]() $\mathscr{F}$
-windows
$\mathscr{F}$
-windows
![]() $\unicode[STIX]{x1D6FE}:\mathscr{P}\times \mathscr{P}^{\prime }\rightarrow \mathscr{P}^{\prime \prime }$
is a bilinear map of
$\unicode[STIX]{x1D6FE}:\mathscr{P}\times \mathscr{P}^{\prime }\rightarrow \mathscr{P}^{\prime \prime }$
is a bilinear map of
![]() $S$
-modules
$S$
-modules
![]() $\unicode[STIX]{x1D6FE}:P\times P^{\prime }\rightarrow P^{\prime \prime }$
that restricts to
$\unicode[STIX]{x1D6FE}:P\times P^{\prime }\rightarrow P^{\prime \prime }$
that restricts to
![]() $Q\times Q^{\prime }\rightarrow Q^{\prime \prime }$
such that for
$Q\times Q^{\prime }\rightarrow Q^{\prime \prime }$
such that for
![]() $x\in Q$
and
$x\in Q$
and
![]() $x^{\prime }\in Q^{\prime }$
we have
$x^{\prime }\in Q^{\prime }$
we have
see [Reference LauLa2, Section 2]. It induces a bilinear map of
![]() $\mathbb{Z}_{p}$
-modules
$\mathbb{Z}_{p}$
-modules
![]() $T(\mathscr{P})\times T(\mathscr{P}^{\prime })\rightarrow T(\mathscr{P}^{\prime \prime })$
and a
$T(\mathscr{P})\times T(\mathscr{P}^{\prime })\rightarrow T(\mathscr{P}^{\prime \prime })$
and a
![]() $\mathbb{Z}_{p}$
-linear map
$\mathbb{Z}_{p}$
-linear map
![]() $T(\mathscr{P})\rightarrow \operatorname{Hom}(\mathscr{P}^{\prime },\mathscr{P}^{\prime \prime })$
. Let us denote the
$T(\mathscr{P})\rightarrow \operatorname{Hom}(\mathscr{P}^{\prime },\mathscr{P}^{\prime \prime })$
. Let us denote the
![]() $\mathscr{F}$
-window
$\mathscr{F}$
-window
![]() $(S,I,\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70E}_{1})$
by
$(S,I,\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70E}_{1})$
by
![]() $\mathscr{F}$
again. For each
$\mathscr{F}$
again. For each
![]() $\mathscr{F}$
-window
$\mathscr{F}$
-window
![]() $\mathscr{P}$
there is a well-defined dual
$\mathscr{P}$
there is a well-defined dual
![]() $\mathscr{F}$
-window
$\mathscr{F}$
-window
![]() $\mathscr{P}^{t}=(P^{t},Q^{t},F^{t},F_{1}^{t})$
with a perfect bilinear form
$\mathscr{P}^{t}=(P^{t},Q^{t},F^{t},F_{1}^{t})$
with a perfect bilinear form
![]() $\mathscr{P}\times \mathscr{P}^{t}\rightarrow \mathscr{F}$
; see [Reference LauLa2, Section 2]. Explicitly,
$\mathscr{P}\times \mathscr{P}^{t}\rightarrow \mathscr{F}$
; see [Reference LauLa2, Section 2]. Explicitly,
![]() $P^{t}=\operatorname{Hom}_{S}(P,S)$
and
$P^{t}=\operatorname{Hom}_{S}(P,S)$
and
![]() $Q^{t}=\{g\in P^{t}\mid g(Q)\subseteq I\}$
; the maps
$Q^{t}=\{g\in P^{t}\mid g(Q)\subseteq I\}$
; the maps
![]() $F_{1}^{t}$
and
$F_{1}^{t}$
and
![]() $F^{t}$
are determined by (3.2) and the window axioms. The resulting homomorphism
$F^{t}$
are determined by (3.2) and the window axioms. The resulting homomorphism
is bijective, which can be verified as follows: We have
![]() $\mathscr{F}^{t}=(S,S,\unicode[STIX]{x1D70E}_{-1},\unicode[STIX]{x1D70E})$
for some
$\mathscr{F}^{t}=(S,S,\unicode[STIX]{x1D70E}_{-1},\unicode[STIX]{x1D70E})$
for some
![]() $\unicode[STIX]{x1D70E}$
-linear map
$\unicode[STIX]{x1D70E}$
-linear map
![]() $\unicode[STIX]{x1D70E}_{-1}$
,Footnote
1
thus
$\unicode[STIX]{x1D70E}_{-1}$
,Footnote
1
thus
![]() $T(\mathscr{P})\cong \operatorname{Hom}(\mathscr{F}^{t},\mathscr{P})$
, which identifies (3.3) with the duality isomorphism
$T(\mathscr{P})\cong \operatorname{Hom}(\mathscr{F}^{t},\mathscr{P})$
, which identifies (3.3) with the duality isomorphism
![]() $\operatorname{Hom}(\mathscr{F}^{t},\mathscr{P})\cong \operatorname{Hom}(\mathscr{P}^{t},\mathscr{F})$
.
$\operatorname{Hom}(\mathscr{F}^{t},\mathscr{P})\cong \operatorname{Hom}(\mathscr{P}^{t},\mathscr{F})$
.
Functoriality of duality
Let
![]() $\unicode[STIX]{x1D6FC}:\mathscr{F}\rightarrow \mathscr{F}^{\prime }$
be a
$\unicode[STIX]{x1D6FC}:\mathscr{F}\rightarrow \mathscr{F}^{\prime }$
be a
![]() $u$
-homomorphism of frames, and let
$u$
-homomorphism of frames, and let
![]() $c$
be as above. For a bilinear form of
$c$
be as above. For a bilinear form of
![]() $\mathscr{F}$
-windows
$\mathscr{F}$
-windows
![]() $\unicode[STIX]{x1D6FE}:\mathscr{P}\times \mathscr{P}^{\prime }\rightarrow \mathscr{P}^{\prime \prime }$
, the base change of
$\unicode[STIX]{x1D6FE}:\mathscr{P}\times \mathscr{P}^{\prime }\rightarrow \mathscr{P}^{\prime \prime }$
, the base change of
![]() $\unicode[STIX]{x1D6FE}$
multiplied by
$\unicode[STIX]{x1D6FE}$
multiplied by
![]() $c^{-1}$
is a bilinear form of
$c^{-1}$
is a bilinear form of
![]() $\mathscr{F}^{\prime }$
-windows
$\mathscr{F}^{\prime }$
-windows
![]() $\unicode[STIX]{x1D6FC}_{\ast }\mathscr{P}\times \unicode[STIX]{x1D6FC}_{\ast }\mathscr{P}^{\prime }\rightarrow \unicode[STIX]{x1D6FC}_{\ast }\mathscr{P}^{\prime \prime }$
, which we denote by
$\unicode[STIX]{x1D6FC}_{\ast }\mathscr{P}\times \unicode[STIX]{x1D6FC}_{\ast }\mathscr{P}^{\prime }\rightarrow \unicode[STIX]{x1D6FC}_{\ast }\mathscr{P}^{\prime \prime }$
, which we denote by
![]() $\unicode[STIX]{x1D6FC}_{\ast }(\unicode[STIX]{x1D6FE})$
; see [Reference LauLa2, Lemma 2.14] and its proof. By passing to the modules of invariants we obtain a commutative diagram
$\unicode[STIX]{x1D6FC}_{\ast }(\unicode[STIX]{x1D6FE})$
; see [Reference LauLa2, Lemma 2.14] and its proof. By passing to the modules of invariants we obtain a commutative diagram

This will be applied to the bilinear form
![]() $\mathscr{P}\times \mathscr{P}^{t}\rightarrow \mathscr{F}$
.
$\mathscr{P}\times \mathscr{P}^{t}\rightarrow \mathscr{F}$
.
4 The case of perfect residue fields
Let
![]() $R,K,k,\mathfrak{m}$
be as in Section 2, and assume in addition that the residue field
$R,K,k,\mathfrak{m}$
be as in Section 2, and assume in addition that the residue field
![]() $k$
is perfect. As in [Reference LauLa3, Sections 2.C and 2.G] we consider the frame
$k$
is perfect. As in [Reference LauLa3, Sections 2.C and 2.G] we consider the frame
Windows over
![]() $\mathscr{D}_{R}$
, called Dieudonné displays over
$\mathscr{D}_{R}$
, called Dieudonné displays over
![]() $R$
, are equivalent to
$R$
, are equivalent to
![]() $p$
-divisible groups
$p$
-divisible groups
![]() $G$
over
$G$
over
![]() $R$
by [Reference ZinkZi2] if
$R$
by [Reference ZinkZi2] if
![]() $p\geqslant 3$
and by [Reference LauLa3, Theorem A] in general. The Tate module
$p\geqslant 3$
and by [Reference LauLa3, Theorem A] in general. The Tate module
![]() $T_{p}(G)$
can be expressed in terms of the Dieudonné display of
$T_{p}(G)$
can be expressed in terms of the Dieudonné display of
![]() $G$
by a variant of Proposition 2.1 as follows.
$G$
by a variant of Proposition 2.1 as follows.
Let
![]() $R^{\operatorname{nr}}$
be the strict Henselization of
$R^{\operatorname{nr}}$
be the strict Henselization of
![]() $R$
. This is a normal local domain, which is excellent by [Reference GrecoGre, Corollary 5.6] or [Reference SeydiSe], and thus its completion
$R$
. This is a normal local domain, which is excellent by [Reference GrecoGre, Corollary 5.6] or [Reference SeydiSe], and thus its completion
![]() $\hat{R}^{\operatorname{nr}}$
is a normal complete noetherian local ring; see EGA IV, (7.8.3.1). Let
$\hat{R}^{\operatorname{nr}}$
is a normal complete noetherian local ring; see EGA IV, (7.8.3.1). Let
![]() $K^{\operatorname{nr}}\subset \hat{K}^{\operatorname{nr}}$
be the fraction fields of the rings
$K^{\operatorname{nr}}\subset \hat{K}^{\operatorname{nr}}$
be the fraction fields of the rings
![]() $R^{\operatorname{nr}}\subset \hat{R}^{\operatorname{nr}}$
, let
$R^{\operatorname{nr}}\subset \hat{R}^{\operatorname{nr}}$
, let
![]() $\tilde{K}$
be an algebraic closure of
$\tilde{K}$
be an algebraic closure of
![]() $\hat{K}^{\operatorname{nr}}$
, and let
$\hat{K}^{\operatorname{nr}}$
, and let
![]() $\tilde{R}$
be the integral closure of
$\tilde{R}$
be the integral closure of
![]() $\hat{R}^{\operatorname{nr}}$
in
$\hat{R}^{\operatorname{nr}}$
in
![]() $\tilde{K}$
. For each finite extension
$\tilde{K}$
. For each finite extension
![]() $E/\hat{K}^{\operatorname{nr}}$
in
$E/\hat{K}^{\operatorname{nr}}$
in
![]() $\tilde{K}$
the ring
$\tilde{K}$
the ring
![]() $R_{E}=\tilde{R}\cap E$
is finite over
$R_{E}=\tilde{R}\cap E$
is finite over
![]() $\hat{R}^{\operatorname{nr}}$
, and
$\hat{R}^{\operatorname{nr}}$
, and
![]() $R_{E}$
is a normal complete noetherian local ring. We define a frame
$R_{E}$
is a normal complete noetherian local ring. We define a frame
where the direct limit is taken componentwise. Here
![]() $\mathbb{W}(\tilde{R})$
is a local ring since all
$\mathbb{W}(\tilde{R})$
is a local ring since all
![]() $\mathbb{W}(R_{E})$
are local with local homomorphisms in between. Since
$\mathbb{W}(R_{E})$
are local with local homomorphisms in between. Since
![]() $\tilde{R}$
has no
$\tilde{R}$
has no
![]() $p$
-torsion, the componentwise
$p$
-torsion, the componentwise
![]() $p$
-adic completion of
$p$
-adic completion of
![]() $\mathscr{D}_{\tilde{R}}$
is a frame
$\mathscr{D}_{\tilde{R}}$
is a frame
There are natural strict frame homomorphisms
![]() $\mathscr{D}_{R}\rightarrow \mathscr{D}_{\tilde{R}}\rightarrow \hat{\mathscr{D}}_{\tilde{R}}$
.
$\mathscr{D}_{R}\rightarrow \mathscr{D}_{\tilde{R}}\rightarrow \hat{\mathscr{D}}_{\tilde{R}}$
.
Let
![]() $\bar{K}$
be the algebraic closure of
$\bar{K}$
be the algebraic closure of
![]() $K$
in
$K$
in
![]() $\tilde{K}$
and let
$\tilde{K}$
and let
![]() ${\mathcal{G}}_{K}=\operatorname{Gal}(\bar{K}/K)$
. The tensor product
${\mathcal{G}}_{K}=\operatorname{Gal}(\bar{K}/K)$
. The tensor product
![]() $\bar{K}\otimes _{K^{\operatorname{nr}}}\hat{K}^{\operatorname{nr}}$
is a subfield of
$\bar{K}\otimes _{K^{\operatorname{nr}}}\hat{K}^{\operatorname{nr}}$
is a subfield of
![]() $\tilde{K}$
. Indeed, this ring is algebraic over
$\tilde{K}$
. Indeed, this ring is algebraic over
![]() $\hat{K}^{\operatorname{nr}}$
, and it is a localization of
$\hat{K}^{\operatorname{nr}}$
, and it is a localization of
![]() $\bar{K}\otimes _{R^{\operatorname{nr}}}\hat{R}^{\operatorname{nr}}$
, which is an integral domain by [Reference RaynaudRa, Chapitre XI, Théorème 3]. If
$\bar{K}\otimes _{R^{\operatorname{nr}}}\hat{R}^{\operatorname{nr}}$
, which is an integral domain by [Reference RaynaudRa, Chapitre XI, Théorème 3]. If
![]() $R$
is one-dimensional, then
$R$
is one-dimensional, then
![]() $\bar{K}\otimes _{K^{\operatorname{nr}}}\hat{K}^{\operatorname{nr}}=\tilde{K}$
because for every
$\bar{K}\otimes _{K^{\operatorname{nr}}}\hat{K}^{\operatorname{nr}}=\tilde{K}$
because for every
![]() $R$
, the étale coverings of the complements of the maximal ideals in
$R$
, the étale coverings of the complements of the maximal ideals in
![]() $\operatorname{Spec}R^{\operatorname{nr}}$
and
$\operatorname{Spec}R^{\operatorname{nr}}$
and
![]() $\operatorname{Spec}\hat{R}^{\operatorname{nr}}$
coincide by [Reference ArtinAr, Part II, Theorem 2.1] or by [Reference ElkikEl, Théorème 5]. Let
$\operatorname{Spec}\hat{R}^{\operatorname{nr}}$
coincide by [Reference ArtinAr, Part II, Theorem 2.1] or by [Reference ElkikEl, Théorème 5]. Let
![]() $\tilde{{\mathcal{G}}}_{K}$
be the group of automorphisms of
$\tilde{{\mathcal{G}}}_{K}$
be the group of automorphisms of
![]() $\tilde{K}$
whose restriction to
$\tilde{K}$
whose restriction to
![]() $\bar{K}\hat{K}^{\operatorname{nr}}$
is induced by an element of
$\bar{K}\hat{K}^{\operatorname{nr}}$
is induced by an element of
![]() ${\mathcal{G}}_{K}$
. This group acts naturally on
${\mathcal{G}}_{K}$
. This group acts naturally on
![]() $\mathscr{D}_{\tilde{R}}$
and on
$\mathscr{D}_{\tilde{R}}$
and on
![]() $\hat{\mathscr{D}}_{\tilde{R}}$
. By the above, the projection
$\hat{\mathscr{D}}_{\tilde{R}}$
. By the above, the projection
![]() $\tilde{{\mathcal{G}}}_{K}\rightarrow {\mathcal{G}}_{K}$
is surjective, and bijective if
$\tilde{{\mathcal{G}}}_{K}\rightarrow {\mathcal{G}}_{K}$
is surjective, and bijective if
![]() $R$
is one-dimensional.
$R$
is one-dimensional.
Proposition 4.1. Let
![]() $G$
be a
$G$
be a
![]() $p$
-divisible group over
$p$
-divisible group over
![]() $R$
and let
$R$
and let
![]() $\mathscr{P}=\unicode[STIX]{x1D6F7}_{R}(G)$
be the Dieudonné display over
$\mathscr{P}=\unicode[STIX]{x1D6F7}_{R}(G)$
be the Dieudonné display over
![]() $R$
associated to
$R$
associated to
![]() $G$
in [Reference LauLa3]. Let
$G$
in [Reference LauLa3]. Let
![]() $\hat{\mathscr{P}}_{\!\tilde{R}}=(\hat{P}_{\tilde{R}},\hat{Q}_{\tilde{R}},F,F_{1})$
be the base change of
$\hat{\mathscr{P}}_{\!\tilde{R}}=(\hat{P}_{\tilde{R}},\hat{Q}_{\tilde{R}},F,F_{1})$
be the base change of
![]() $\mathscr{P}$
to
$\mathscr{P}$
to
![]() $\hat{\mathscr{D}}_{\tilde{R}}$
. There is a natural exact sequence of
$\hat{\mathscr{D}}_{\tilde{R}}$
. There is a natural exact sequence of
![]() $\tilde{{\mathcal{G}}}_{K}$
-modules
$\tilde{{\mathcal{G}}}_{K}$
-modules
In particular, we have an isomorphism of
![]() ${\mathcal{G}}_{K}$
-modules
${\mathcal{G}}_{K}$
-modules
which we call the period isomorphism in display theory.
Proof of Proposition 4.1.
For a finite extension
![]() $E/\hat{K}^{\operatorname{nr}}$
in
$E/\hat{K}^{\operatorname{nr}}$
in
![]() $\tilde{K}$
let
$\tilde{K}$
let
![]() $\mathfrak{m}_{E}$
be the maximal ideal of
$\mathfrak{m}_{E}$
be the maximal ideal of
![]() $R_{E}$
. For a
$R_{E}$
. For a
![]() $p$
-divisible group
$p$
-divisible group
![]() $G$
over
$G$
over
![]() $R$
we set
$R$
we set
The group
![]() $\tilde{{\mathcal{G}}}_{K}$
acts on the system
$\tilde{{\mathcal{G}}}_{K}$
acts on the system
![]() ${\hat{G}}(R_{E})$
for varying
${\hat{G}}(R_{E})$
for varying
![]() $E$
and thus on
$E$
and thus on
![]() ${\hat{G}}(\tilde{R})$
. The latter can be described using [Reference LauLa3, Section 9] as follows.
${\hat{G}}(\tilde{R})$
. The latter can be described using [Reference LauLa3, Section 9] as follows.
Following [Reference LauLa3, Definition 9.1] let
![]() ${\mathcal{J}}_{n}={\mathcal{J}}_{R/\mathfrak{m}^{n}}$
be the category of all
${\mathcal{J}}_{n}={\mathcal{J}}_{R/\mathfrak{m}^{n}}$
be the category of all
![]() $R/\mathfrak{m}^{n}$
-algebras
$R/\mathfrak{m}^{n}$
-algebras
![]() $A$
such that the nilradical
$A$
such that the nilradical
![]() ${\mathcal{N}}_{A}$
is bounded nilpotent and such that
${\mathcal{N}}_{A}$
is bounded nilpotent and such that
![]() $A/{\mathcal{N}}_{A}$
is a union of finite-dimensional
$A/{\mathcal{N}}_{A}$
is a union of finite-dimensional
![]() $k$
-algebras. Let
$k$
-algebras. Let
![]() $\mathscr{P}_{n}$
be the base change of
$\mathscr{P}_{n}$
be the base change of
![]() $\mathscr{P}$
to
$\mathscr{P}$
to
![]() $R/\mathfrak{m}^{n}$
, and for
$R/\mathfrak{m}^{n}$
, and for
![]() $A\in {\mathcal{J}}_{n}$
let
$A\in {\mathcal{J}}_{n}$
let
![]() $\mathscr{P}_{A}=(P_{A},Q_{A},F,F_{1})$
be the base change of
$\mathscr{P}_{A}=(P_{A},Q_{A},F,F_{1})$
be the base change of
![]() $\mathscr{P}$
to
$\mathscr{P}$
to
![]() $A$
. As in [Reference LauLa3, (9–2)] we define a complex of presheaves
$A$
. As in [Reference LauLa3, (9–2)] we define a complex of presheaves
![]() $Z^{\prime }(\mathscr{P}_{n})$
on
$Z^{\prime }(\mathscr{P}_{n})$
on
![]() ${\mathcal{J}}_{n}^{\operatorname{op}}$
whose value on
${\mathcal{J}}_{n}^{\operatorname{op}}$
whose value on
![]() $A$
is the complex of abelian groups
$A$
is the complex of abelian groups
in degrees
![]() $-1,0,1$
. By [Reference LauLa3, Proposition 9.4],
$-1,0,1$
. By [Reference LauLa3, Proposition 9.4],
![]() $Z^{\prime }(\mathscr{P}_{n})$
is a complex of pro-étale sheaves on
$Z^{\prime }(\mathscr{P}_{n})$
is a complex of pro-étale sheaves on
![]() ${\mathcal{J}}_{n}^{\operatorname{op}}$
, which is acyclic outside degree zero, and the middle cohomology sheaf
${\mathcal{J}}_{n}^{\operatorname{op}}$
, which is acyclic outside degree zero, and the middle cohomology sheaf
![]() $H^{0}(Z^{\prime }(\mathscr{P}))$
is represented by a well-defined
$H^{0}(Z^{\prime }(\mathscr{P}))$
is represented by a well-defined
![]() $p$
-divisible group
$p$
-divisible group
![]() $\operatorname{BT}(\mathscr{P})$
over
$\operatorname{BT}(\mathscr{P})$
over
![]() $R$
. By [Reference LauLa3, Proposition 9.7] there is a canonical isomorphism
$R$
. By [Reference LauLa3, Proposition 9.7] there is a canonical isomorphism
![]() $G\cong \operatorname{BT}(\mathscr{P})$
.
$G\cong \operatorname{BT}(\mathscr{P})$
.
The ring
![]() $R_{E,n}=R_{E}/\mathfrak{m}_{E}^{n}$
is a local Artin ring with residue field
$R_{E,n}=R_{E}/\mathfrak{m}_{E}^{n}$
is a local Artin ring with residue field
![]() $\bar{k}$
, and thus it lies in
$\bar{k}$
, and thus it lies in
![]() ${\mathcal{J}}_{n}$
. Every pro-étale covering of
${\mathcal{J}}_{n}$
. Every pro-étale covering of
![]() $\operatorname{Spec}R_{E,n}$
has a section since every étale covering of
$\operatorname{Spec}R_{E,n}$
has a section since every étale covering of
![]() $\operatorname{Spec}R_{E,n}$
has a nonempty finite set of sections, and the projective limit of a projective system of nonempty finite sets is nonempty by [SP, Tag 086J]. Hence evaluating pro-étale sheaves at
$\operatorname{Spec}R_{E,n}$
has a nonempty finite set of sections, and the projective limit of a projective system of nonempty finite sets is nonempty by [SP, Tag 086J]. Hence evaluating pro-étale sheaves at
![]() $R_{E,n}$
is an exact functor. It follows that the complex of abelian groups
$R_{E,n}$
is an exact functor. It follows that the complex of abelian groups
in degrees
![]() $-1,0,1$
is acyclic outside degree zero, and there is a canonical isomorphism
$-1,0,1$
is acyclic outside degree zero, and there is a canonical isomorphism
![]() $G(R_{E,n})\cong H^{0}(C_{E,n})$
. For varying
$G(R_{E,n})\cong H^{0}(C_{E,n})$
. For varying
![]() $n$
and
$n$
and
![]() $E$
these are preserved by the action of
$E$
these are preserved by the action of
![]() $\tilde{{\mathcal{G}}}_{K}$
. Let
$\tilde{{\mathcal{G}}}_{K}$
. Let
where
![]() $E$
runs through the finite extensions of
$E$
runs through the finite extensions of
![]() $\hat{K}^{\operatorname{nr}}$
in
$\hat{K}^{\operatorname{nr}}$
in
![]() $\tilde{K}$
. The group
$\tilde{K}$
. The group
![]() $\tilde{{\mathcal{G}}}_{K}$
acts on the complex
$\tilde{{\mathcal{G}}}_{K}$
acts on the complex
![]() $C$
. Since the groups
$C$
. Since the groups
![]() $G(R_{E,n})$
and the components of
$G(R_{E,n})$
and the components of
![]() $C_{E,n}$
form surjective systems with respect to
$C_{E,n}$
form surjective systems with respect to
![]() $n$
, the complex
$n$
, the complex
![]() $C$
is acyclic outside degree zero, and we have an isomorphism of
$C$
is acyclic outside degree zero, and we have an isomorphism of
![]() $\tilde{{\mathcal{G}}}_{K}$
-modules
$\tilde{{\mathcal{G}}}_{K}$
-modules
![]() ${\hat{G}}(\tilde{R})\cong H^{0}(C)$
. We will verify the following chain of isomorphisms
${\hat{G}}(\tilde{R})\cong H^{0}(C)$
. We will verify the following chain of isomorphisms
![]() $\cong$
and quasi-isomorphisms
$\cong$
and quasi-isomorphisms
![]() $\simeq$
of complexes of
$\simeq$
of complexes of
![]() $\tilde{{\mathcal{G}}}_{K}$
-modules, where
$\tilde{{\mathcal{G}}}_{K}$
-modules, where
![]() $\operatorname{Hom}$
,
$\operatorname{Hom}$
,
![]() $R\operatorname{Hom}$
, and
$R\operatorname{Hom}$
, and
![]() $\operatorname{Ext}^{1}$
are taken in the category of abelian groups using a projective resolution of
$\operatorname{Ext}^{1}$
are taken in the category of abelian groups using a projective resolution of
![]() $\mathbb{Q}_{p}/\mathbb{Z}_{p}$
, in particular
$\mathbb{Q}_{p}/\mathbb{Z}_{p}$
, in particular
![]() $\operatorname{Ext}^{1}$
is taken componentwise with respect to the second argument.
$\operatorname{Ext}^{1}$
is taken componentwise with respect to the second argument.
 $$\begin{eqnarray}\displaystyle T_{p}(G) & \underset{(1)}{\cong } & \displaystyle \operatorname{Hom}(\mathbb{Q}_{p}/\mathbb{Z}_{p},{\hat{G}}(\tilde{R}))\underset{(2)}{\simeq }R\operatorname{Hom}(\mathbb{Q}_{p}/\mathbb{Z}_{p},{\hat{G}}(\tilde{R}))\nonumber\\ \displaystyle & \underset{(3)}{\simeq } & \displaystyle R\operatorname{Hom}(\mathbb{Q}_{p}/\mathbb{Z}_{p},C)\underset{(4)}{\simeq }\operatorname{Ext}^{1}(\mathbb{Q}_{p}/\mathbb{Z}_{p},C[-1])\underset{(5)}{\cong }[\hat{Q}_{\tilde{R}}\xrightarrow[{}]{F_{1}-1}\hat{P}_{\tilde{R}}]\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle T_{p}(G) & \underset{(1)}{\cong } & \displaystyle \operatorname{Hom}(\mathbb{Q}_{p}/\mathbb{Z}_{p},{\hat{G}}(\tilde{R}))\underset{(2)}{\simeq }R\operatorname{Hom}(\mathbb{Q}_{p}/\mathbb{Z}_{p},{\hat{G}}(\tilde{R}))\nonumber\\ \displaystyle & \underset{(3)}{\simeq } & \displaystyle R\operatorname{Hom}(\mathbb{Q}_{p}/\mathbb{Z}_{p},C)\underset{(4)}{\simeq }\operatorname{Ext}^{1}(\mathbb{Q}_{p}/\mathbb{Z}_{p},C[-1])\underset{(5)}{\cong }[\hat{Q}_{\tilde{R}}\xrightarrow[{}]{F_{1}-1}\hat{P}_{\tilde{R}}]\nonumber\end{eqnarray}$$
This will prove the proposition.
The torsion subgroups of
![]() $G(\bar{K})$
and of
$G(\bar{K})$
and of
![]() ${\hat{G}}(\tilde{R})$
coincide by Lemma 2.4 applied over
${\hat{G}}(\tilde{R})$
coincide by Lemma 2.4 applied over
![]() $\hat{R}^{\operatorname{nr}}$
, and (1) follows. Multiplication by
$\hat{R}^{\operatorname{nr}}$
, and (1) follows. Multiplication by
![]() $p$
is surjective on
$p$
is surjective on
![]() ${\hat{G}}(\tilde{R})$
by Lemma 2.3 applied over
${\hat{G}}(\tilde{R})$
by Lemma 2.3 applied over
![]() $\hat{R}^{\operatorname{nr}}$
, thus Lemma 2.2 gives
$\hat{R}^{\operatorname{nr}}$
, thus Lemma 2.2 gives
![]() $\operatorname{Ext}^{1}(\mathbb{Q}_{p}/\mathbb{Z}_{p},{\hat{G}}(\tilde{R}))=0$
, which proves (2). Since the cohomology of
$\operatorname{Ext}^{1}(\mathbb{Q}_{p}/\mathbb{Z}_{p},{\hat{G}}(\tilde{R}))=0$
, which proves (2). Since the cohomology of
![]() $C$
is
$C$
is
![]() ${\hat{G}}(\tilde{R})$
in degree zero and zero otherwise, we obtain (3). To prove (4) we choose an exact sequence of abelian groups
${\hat{G}}(\tilde{R})$
in degree zero and zero otherwise, we obtain (3). To prove (4) we choose an exact sequence of abelian groups
![]() $0\rightarrow F_{1}\rightarrow F_{0}\rightarrow \mathbb{Q}_{p}/\mathbb{Z}_{p}\rightarrow 0$
with free
$0\rightarrow F_{1}\rightarrow F_{0}\rightarrow \mathbb{Q}_{p}/\mathbb{Z}_{p}\rightarrow 0$
with free
![]() $F_{i}$
. This gives an exact sequence of complexes of
$F_{i}$
. This gives an exact sequence of complexes of
![]() $\tilde{{\mathcal{G}}}_{K}$
-modules
$\tilde{{\mathcal{G}}}_{K}$
-modules
We claim that
![]() $\operatorname{Hom}(\mathbb{Q}_{p}/\mathbb{Z}_{p},C)$
is zero. Then the complex
$\operatorname{Hom}(\mathbb{Q}_{p}/\mathbb{Z}_{p},C)$
is zero. Then the complex
![]() $\operatorname{Ext}^{1}(\mathbb{Q}_{p}/\mathbb{Z}_{p},C)[-1]$
is quasi-isomorphic to the cone of
$\operatorname{Ext}^{1}(\mathbb{Q}_{p}/\mathbb{Z}_{p},C)[-1]$
is quasi-isomorphic to the cone of
![]() $u$
, which represents
$u$
, which represents
![]() $R\operatorname{Hom}(\mathbb{Q}_{p}/\mathbb{Z}_{p},C)$
, and (4) follows. Let
$R\operatorname{Hom}(\mathbb{Q}_{p}/\mathbb{Z}_{p},C)$
, and (4) follows. Let
![]() $(P_{\tilde{R}},Q_{\tilde{R}},F,F_{1})$
be the base change of
$(P_{\tilde{R}},Q_{\tilde{R}},F,F_{1})$
be the base change of
![]() $\mathscr{P}$
to
$\mathscr{P}$
to
![]() $\mathscr{D}_{\tilde{R}}$
and let
$\mathscr{D}_{\tilde{R}}$
and let
![]() $P_{\bar{k}}=W(\bar{k})\otimes _{\mathbb{W}(R)}P$
. We have
$P_{\bar{k}}=W(\bar{k})\otimes _{\mathbb{W}(R)}P$
. We have
![]() $Q_{R_{E,n}}[1/p]=P_{R_{E,n}}[1/p]=P_{\bar{k}}[1/p]$
because the cokernel of the inclusion
$Q_{R_{E,n}}[1/p]=P_{R_{E,n}}[1/p]=P_{\bar{k}}[1/p]$
because the cokernel of the inclusion
![]() $Q_{R_{E,n}}\rightarrow P_{R_{E,n}}$
is an
$Q_{R_{E,n}}\rightarrow P_{R_{E,n}}$
is an
![]() $R_{E,n}$
-module and thus
$R_{E,n}$
-module and thus
![]() $p$
-power torsion, and the kernel of the surjective map
$p$
-power torsion, and the kernel of the surjective map
![]() $P_{R_{E,n}}\rightarrow P_{\bar{k}}$
is
$P_{R_{E,n}}\rightarrow P_{\bar{k}}$
is
![]() $p$
-power torsion by [Reference ZinkZi3, Lemma 2.2]. Thus the complex
$p$
-power torsion by [Reference ZinkZi3, Lemma 2.2]. Thus the complex
![]() $C$
can be identified with the cone of the map of complexes
$C$
can be identified with the cone of the map of complexes
Since
![]() $\tilde{R}$
is a domain of characteristic zero, the ring
$\tilde{R}$
is a domain of characteristic zero, the ring
![]() $W(\tilde{R})$
has no
$W(\tilde{R})$
has no
![]() $p$
-torsion. Since
$p$
-torsion. Since
![]() $\mathbb{W}(\tilde{R})$
is a subring of
$\mathbb{W}(\tilde{R})$
is a subring of
![]() $W(\tilde{R})$
the projective
$W(\tilde{R})$
the projective
![]() $\mathbb{W}(\tilde{R})$
-module
$\mathbb{W}(\tilde{R})$
-module
![]() $P_{\tilde{R}}$
and its submodule
$P_{\tilde{R}}$
and its submodule
![]() $Q_{\tilde{R}}$
have no
$Q_{\tilde{R}}$
have no
![]() $p$
-torsion. Clearly
$p$
-torsion. Clearly
![]() $P_{\bar{k}}[1/p]$
has no
$P_{\bar{k}}[1/p]$
has no
![]() $p$
-torsion. Hence
$p$
-torsion. Hence
![]() $\operatorname{Hom}(\mathbb{Q}_{p}/\mathbb{Z}_{p},C)$
is zero, and (4) is proved. The
$\operatorname{Hom}(\mathbb{Q}_{p}/\mathbb{Z}_{p},C)$
is zero, and (4) is proved. The
![]() $p$
-adic completions of
$p$
-adic completions of
![]() $P_{\tilde{R}}$
and
$P_{\tilde{R}}$
and
![]() $Q_{\tilde{R}}$
are
$Q_{\tilde{R}}$
are
![]() $\hat{P}_{\tilde{R}}$
and
$\hat{P}_{\tilde{R}}$
and
![]() $\hat{Q}_{\tilde{R}}$
, while the
$\hat{Q}_{\tilde{R}}$
, while the
![]() $p$
-adic completion of
$p$
-adic completion of
![]() $P_{\bar{k}}[1/p]$
is zero. Thus Lemma 2.2 gives (5).◻
$P_{\bar{k}}[1/p]$
is zero. Thus Lemma 2.2 gives (5).◻
Remark 4.2. Let
![]() $G_{0}=\mathbb{Q}_{p}/\mathbb{Z}_{p}$
. The isomorphisms
$G_{0}=\mathbb{Q}_{p}/\mathbb{Z}_{p}$
. The isomorphisms
![]() $\operatorname{per}_{G}$
for all
$\operatorname{per}_{G}$
for all
![]() $G$
can be altered by multiplication with a common
$G$
can be altered by multiplication with a common
![]() $p$
-adic unit. This allows to assume that
$p$
-adic unit. This allows to assume that
![]() $\operatorname{per}_{G_{0}}$
is the identity of
$\operatorname{per}_{G_{0}}$
is the identity of
![]() $\mathbb{Z}_{p}$
in the following sense. Clearly
$\mathbb{Z}_{p}$
in the following sense. Clearly
![]() $T_{p}(G_{0})=\mathbb{Z}_{p}$
. The Dieudonné display of
$T_{p}(G_{0})=\mathbb{Z}_{p}$
. The Dieudonné display of
![]() $\unicode[STIX]{x1D707}_{p^{\infty }}$
is
$\unicode[STIX]{x1D707}_{p^{\infty }}$
is
![]() $\mathscr{D}_{R}=(\mathbb{W}(R),\mathbb{I}_{R},f,f_{1})$
, and thus the Dieudonné display of
$\mathscr{D}_{R}=(\mathbb{W}(R),\mathbb{I}_{R},f,f_{1})$
, and thus the Dieudonné display of
![]() $G_{0}$
is the dual
$G_{0}$
is the dual
![]() $\mathscr{D}_{R}^{t}=(\mathbb{W}(R),\mathbb{W}(R),pu_{0}f,f)$
; cf. [Reference LauLa3, Section 2.C]. Then
$\mathscr{D}_{R}^{t}=(\mathbb{W}(R),\mathbb{W}(R),pu_{0}f,f)$
; cf. [Reference LauLa3, Section 2.C]. Then
![]() $T(\hat{\mathscr{D}}_{\tilde{R}}^{t})=\hat{\mathbb{W}}(\tilde{R})^{f=1}=\mathbb{Z}_{p}$
by Lemma 4.3 below, and
$T(\hat{\mathscr{D}}_{\tilde{R}}^{t})=\hat{\mathbb{W}}(\tilde{R})^{f=1}=\mathbb{Z}_{p}$
by Lemma 4.3 below, and
![]() $\operatorname{per}_{G_{0}}$
can be viewed as a
$\operatorname{per}_{G_{0}}$
can be viewed as a
![]() $\mathbb{Z}_{p}$
-linear automorphism of
$\mathbb{Z}_{p}$
-linear automorphism of
![]() $\mathbb{Z}_{p}$
.
$\mathbb{Z}_{p}$
.
We note that the construction in the proof of Proposition 4.1 actually defines
![]() $\operatorname{per}_{G}$
only up to multiplication by a common
$\operatorname{per}_{G}$
only up to multiplication by a common
![]() $p$
-adic unit because it uses the isomorphism
$p$
-adic unit because it uses the isomorphism
![]() $\operatorname{BT}(\mathscr{P})\cong G$
provided by [Reference LauLa3, Proposition 9.7], which relies on [Reference LauLa3, Lemma 8.2], and that takes as an input the choice of such an isomorphism for
$\operatorname{BT}(\mathscr{P})\cong G$
provided by [Reference LauLa3, Proposition 9.7], which relies on [Reference LauLa3, Lemma 8.2], and that takes as an input the choice of such an isomorphism for
![]() $G_{0}$
.
$G_{0}$
.
Lemma 4.3. Let
![]() $S$
be a
$S$
be a
![]() $p$
-adic torsion free ring with a Frobenius lift
$p$
-adic torsion free ring with a Frobenius lift
![]() $\unicode[STIX]{x1D70E}:S\rightarrow S$
. If
$\unicode[STIX]{x1D70E}:S\rightarrow S$
. If
![]() $\operatorname{Spec}(S/pS)$
is connected, for example if
$\operatorname{Spec}(S/pS)$
is connected, for example if
![]() $S$
is a local ring, then
$S$
is a local ring, then
![]() $S^{\unicode[STIX]{x1D70E}=1}=\mathbb{Z}_{p}$
.
$S^{\unicode[STIX]{x1D70E}=1}=\mathbb{Z}_{p}$
.
Proof. It suffices to show that
![]() $(S/p^{n})^{\unicode[STIX]{x1D70E}=1}=\mathbb{Z}/p^{n}$
. The case
$(S/p^{n})^{\unicode[STIX]{x1D70E}=1}=\mathbb{Z}/p^{n}$
. The case
![]() $n=1$
holds because the polynomial
$n=1$
holds because the polynomial
![]() $X^{p}-X=\prod _{a\in \mathbb{F}_{p}}(X-a)$
is separable. The general case follows by induction using the exact sequences
$X^{p}-X=\prod _{a\in \mathbb{F}_{p}}(X-a)$
is separable. The general case follows by induction using the exact sequences
![]() $0\rightarrow S/p\xrightarrow[{p^{n}}]{}S/p^{n+1}\rightarrow S/p^{n}\rightarrow 0$
.◻
$0\rightarrow S/p\xrightarrow[{p^{n}}]{}S/p^{n+1}\rightarrow S/p^{n}\rightarrow 0$
.◻
5 A variant for the prime
 $2$
$2$
We keep the notation and assumptions of Section 4 and assume that
![]() $p=2$
. One can ask what the preceding constructions give when
$p=2$
. One can ask what the preceding constructions give when
![]() $\mathbb{W}$
and
$\mathbb{W}$
and
![]() $\mathscr{D}$
are replaced by their
$\mathscr{D}$
are replaced by their
![]() $v$
-stabilized variants
$v$
-stabilized variants
![]() $\mathbb{W}^{+}$
and
$\mathbb{W}^{+}$
and
![]() $\mathscr{D}^{+}$
defined in [Reference LauLa3, Sections 1.D, 2.E]. This will be used in Section 6. We recall that
$\mathscr{D}^{+}$
defined in [Reference LauLa3, Sections 1.D, 2.E]. This will be used in Section 6. We recall that
![]() $\mathbb{W}(R)\subset \mathbb{W}^{+}(R)\subset W(R)$
where the ring
$\mathbb{W}(R)\subset \mathbb{W}^{+}(R)\subset W(R)$
where the ring
![]() $\mathbb{W}^{+}(R)$
is stable under
$\mathbb{W}^{+}(R)$
is stable under
![]() $v$
, and we have a frame
$v$
, and we have a frame
where
![]() $f_{1}$
is the inverse of
$f_{1}$
is the inverse of
![]() $v$
. As earlier we put
$v$
. As earlier we put
where
![]() $E$
runs through the finite extensions of
$E$
runs through the finite extensions of
![]() $\hat{K}^{\operatorname{nr}}$
in
$\hat{K}^{\operatorname{nr}}$
in
![]() $\tilde{K}$
as in Section 4, and we denote the componentwise
$\tilde{K}$
as in Section 4, and we denote the componentwise
![]() $2$
-adic completion of
$2$
-adic completion of
![]() $\mathscr{D}_{\tilde{R}}^{+}$
by
$\mathscr{D}_{\tilde{R}}^{+}$
by
For a
![]() $2$
-divisible group
$2$
-divisible group
![]() $G$
over
$G$
over
![]() $R$
let
$R$
let
![]() $G^{m}$
and
$G^{m}$
and
![]() $G^{u}$
be the multiplicative and unipotent parts of
$G^{u}$
be the multiplicative and unipotent parts of
![]() $G$
and define
$G$
and define
![]() $G^{+}$
as a pushout of fppf sheaves in the following diagram.
$G^{+}$
as a pushout of fppf sheaves in the following diagram.

The rows of (5.1) are exact, so
![]() $G^{+}$
is a
$G^{+}$
is a
![]() $2$
-divisible group by [Reference MessingMe1, Chapter I, (2.4.3)]. On the level of Tate modules (5.1) gives a commutative diagram with exact rows
$2$
-divisible group by [Reference MessingMe1, Chapter I, (2.4.3)]. On the level of Tate modules (5.1) gives a commutative diagram with exact rows

which shows that
![]() $T_{2}(G^{+})$
is the pushout in the left hand square as a Galois module.
$T_{2}(G^{+})$
is the pushout in the left hand square as a Galois module.
Proposition 5.1. Let
![]() $G$
be a
$G$
be a
![]() $2$
-divisible group over
$2$
-divisible group over
![]() $R$
with associated Dieudonné display
$R$
with associated Dieudonné display
![]() $\mathscr{P}=\unicode[STIX]{x1D6F7}_{R}(G)$
. Let
$\mathscr{P}=\unicode[STIX]{x1D6F7}_{R}(G)$
. Let
![]() $\hat{\mathscr{P}}_{\!\tilde{R}}^{+}=(\hat{P}_{\tilde{R}}^{+},\hat{Q}_{\tilde{R}}^{+},F,F_{1}^{+})$
be the base change of
$\hat{\mathscr{P}}_{\!\tilde{R}}^{+}=(\hat{P}_{\tilde{R}}^{+},\hat{Q}_{\tilde{R}}^{+},F,F_{1}^{+})$
be the base change of
![]() $\mathscr{P}$
to
$\mathscr{P}$
to
![]() $\hat{\mathscr{D}}_{\tilde{R}}^{+}$
. There is a natural exact sequence of
$\hat{\mathscr{D}}_{\tilde{R}}^{+}$
. There is a natural exact sequence of
![]() $\tilde{{\mathcal{G}}}_{K}$
-modules
$\tilde{{\mathcal{G}}}_{K}$
-modules
In particular, we have an isomorphism of
![]() ${\mathcal{G}}_{K}$
-modules
${\mathcal{G}}_{K}$
-modules
Proof. Let
![]() $\bar{P}_{\bar{k}}=\bar{k}\otimes _{\mathbb{W}(R)}P$
. We will construct the following commutative diagram with exact rows, where
$\bar{P}_{\bar{k}}=\bar{k}\otimes _{\mathbb{W}(R)}P$
. We will construct the following commutative diagram with exact rows, where
![]() $\bar{F}$
is induced by
$\bar{F}$
is induced by
![]() $F$
.
$F$
.

Assume that (5.3) is constructed and functorial in
![]() $G$
. Since
$G$
. Since
![]() $\bar{P}_{\bar{k}}=\bar{k}\otimes _{\mathbb{W}(R)}P$
is the reduction mod
$\bar{P}_{\bar{k}}=\bar{k}\otimes _{\mathbb{W}(R)}P$
is the reduction mod
![]() $2$
of the covariant Dieudonné module of
$2$
of the covariant Dieudonné module of
![]() $G_{\bar{k}}$
, the Frobenius-linear endomorphism
$G_{\bar{k}}$
, the Frobenius-linear endomorphism
![]() $\bar{F}$
is nilpotent if
$\bar{F}$
is nilpotent if
![]() $G$
is unipotent, and is given by an invertible matrix if
$G$
is unipotent, and is given by an invertible matrix if
![]() $G$
is of multiplicative type. Thus
$G$
is of multiplicative type. Thus
![]() $\bar{F}-1$
is surjective with kernel an
$\bar{F}-1$
is surjective with kernel an
![]() $\mathbb{F}_{2}$
-vector space of dimension equal to the height of
$\mathbb{F}_{2}$
-vector space of dimension equal to the height of
![]() $G^{m}$
. Hence Proposition 4.1 implies that
$G^{m}$
. Hence Proposition 4.1 implies that
![]() $F_{1}^{+}-1$
is surjective and gives an exact sequence
$F_{1}^{+}-1$
is surjective and gives an exact sequence
The ring
![]() $W(\tilde{R})$
and its subring
$W(\tilde{R})$
and its subring
![]() $\mathbb{W}^{+}(\tilde{R})$
are torsion free, which carries over to the
$\mathbb{W}^{+}(\tilde{R})$
are torsion free, which carries over to the
![]() $2$
-adic completion, hence
$2$
-adic completion, hence
![]() $T(\hat{\mathscr{P}}_{\!\tilde{R}}^{+})$
is torsion free. It follows that
$T(\hat{\mathscr{P}}_{\!\tilde{R}}^{+})$
is torsion free. It follows that
![]() $T(\hat{\mathscr{P}}_{\!\tilde{R}}^{+})=T_{2}(G)$
if
$T(\hat{\mathscr{P}}_{\!\tilde{R}}^{+})=T_{2}(G)$
if
![]() $G$
is unipotent, and multiplication by
$G$
is unipotent, and multiplication by
![]() $2$
gives an isomorphism
$2$
gives an isomorphism
![]() $T(\hat{\mathscr{P}}_{\!\tilde{R}}^{+})\rightarrow T_{2}(G)$
if
$T(\hat{\mathscr{P}}_{\!\tilde{R}}^{+})\rightarrow T_{2}(G)$
if
![]() $G$
is multiplicative type. Hence there is a pushout diagram (5.2) with
$G$
is multiplicative type. Hence there is a pushout diagram (5.2) with
![]() $T(\hat{\mathscr{P}}_{\!\tilde{R}}^{+})$
in place of
$T(\hat{\mathscr{P}}_{\!\tilde{R}}^{+})$
in place of
![]() $T_{2}(G^{+})$
, which gives an isomorphism between these modules as required.
$T_{2}(G^{+})$
, which gives an isomorphism between these modules as required.
Let us construct (5.3). [Reference LauLa3, Lemma 1.10] implies that the inclusion map
![]() $\mathbb{W}(R_{E}/\mathfrak{m}_{E}^{n})\rightarrow \mathbb{W}^{+}(R_{E}/\mathfrak{m}_{E}^{n})$
is bijective when
$\mathbb{W}(R_{E}/\mathfrak{m}_{E}^{n})\rightarrow \mathbb{W}^{+}(R_{E}/\mathfrak{m}_{E}^{n})$
is bijective when
![]() $2\in \mathfrak{m}_{E}^{n}$
, and its cokernel is
$2\in \mathfrak{m}_{E}^{n}$
, and its cokernel is
![]() $\bar{k}\cdot v(1)$
as a
$\bar{k}\cdot v(1)$
as a
![]() $\mathbb{W}(R_{E})$
-module when
$\mathbb{W}(R_{E})$
-module when
![]() $2\not \in \mathfrak{m}_{E}^{n}$
. It follows that the natural map
$2\not \in \mathfrak{m}_{E}^{n}$
. It follows that the natural map
![]() $\unicode[STIX]{x1D704}:\hat{\mathbb{W}}(\tilde{R})\rightarrow \hat{\mathbb{W}}^{+}(\tilde{R})$
is injective with cokernel
$\unicode[STIX]{x1D704}:\hat{\mathbb{W}}(\tilde{R})\rightarrow \hat{\mathbb{W}}^{+}(\tilde{R})$
is injective with cokernel
Moreover
![]() $\unicode[STIX]{x1D704}$
is a
$\unicode[STIX]{x1D704}$
is a
![]() $u_{0}$
-homomorphism of frames
$u_{0}$
-homomorphism of frames
![]() $\hat{\mathscr{D}}_{\tilde{R}}\rightarrow \hat{\mathscr{D}}_{\tilde{R}}^{+}$
where the unit
$\hat{\mathscr{D}}_{\tilde{R}}\rightarrow \hat{\mathscr{D}}_{\tilde{R}}^{+}$
where the unit
![]() $u_{0}\in \mathbb{W}^{+}(\mathbb{Z}_{2})$
is defined by
$u_{0}\in \mathbb{W}^{+}(\mathbb{Z}_{2})$
is defined by
![]() $v(u_{0})=2-[2]$
; see [Reference LauLa3, Section 2.E]. Since
$v(u_{0})=2-[2]$
; see [Reference LauLa3, Section 2.E]. Since
![]() $u_{0}$
maps to
$u_{0}$
maps to
![]() $1$
in
$1$
in
![]() $W(\mathbb{F}_{2})$
there is a unique unit
$W(\mathbb{F}_{2})$
there is a unique unit
![]() $c_{0}$
of
$c_{0}$
of
![]() $\mathbb{W}^{+}(\mathbb{Z}_{2})$
which maps to
$\mathbb{W}^{+}(\mathbb{Z}_{2})$
which maps to
![]() $1$
in
$1$
in
![]() $W(\mathbb{F}_{2})$
such that
$W(\mathbb{F}_{2})$
such that
![]() $c_{0}f(c_{0}^{-1})=u_{0}$
, namely
$c_{0}f(c_{0}^{-1})=u_{0}$
, namely
![]() $c_{0}=u_{0}f(u_{0})f^{2}(u_{0})\cdots \,$
; see the proof of [Reference LauLa2, Proposition 8.7].
$c_{0}=u_{0}f(u_{0})f^{2}(u_{0})\cdots \,$
; see the proof of [Reference LauLa2, Proposition 8.7].
We extend the operator
![]() $f_{1}$
of
$f_{1}$
of
![]() $\hat{\mathscr{D}}_{\tilde{R}}$
to
$\hat{\mathscr{D}}_{\tilde{R}}$
to
![]() $\hat{\mathscr{D}}_{\tilde{R}}^{+}$
by
$\hat{\mathscr{D}}_{\tilde{R}}^{+}$
by
![]() $f_{1}=u_{0}^{-1}f_{1}$
. Then
$f_{1}=u_{0}^{-1}f_{1}$
. Then
![]() $f_{1}$
induces an
$f_{1}$
induces an
![]() $f$
-linear endomorphism
$f$
-linear endomorphism
![]() $\bar{f}_{1}$
of
$\bar{f}_{1}$
of
![]() $\bar{k}\cdot v(1)$
. We claim that
$\bar{k}\cdot v(1)$
. We claim that
![]() $\bar{f}_{1}(v(1))=v(1)$
. It suffices to prove this formula in
$\bar{f}_{1}(v(1))=v(1)$
. It suffices to prove this formula in
![]() $\mathbb{W}^{+}(\mathbb{Z}_{2})/\mathbb{W}(\mathbb{Z}_{2})\cong \mathbb{F}_{2}$
, and thus it suffices to show that
$\mathbb{W}^{+}(\mathbb{Z}_{2})/\mathbb{W}(\mathbb{Z}_{2})\cong \mathbb{F}_{2}$
, and thus it suffices to show that
![]() $f_{1}(v(1))\not \in \mathbb{W}(\mathbb{Z}_{2})$
. But
$f_{1}(v(1))\not \in \mathbb{W}(\mathbb{Z}_{2})$
. But
![]() $\mathbb{W}(\mathbb{Z}_{2})$
is stable under
$\mathbb{W}(\mathbb{Z}_{2})$
is stable under
![]() $x\mapsto v(x)=v(u_{0}x)$
, and the element
$x\mapsto v(x)=v(u_{0}x)$
, and the element
![]() $v(f_{1}(v(1)))=v(1)$
does not lie in
$v(f_{1}(v(1)))=v(1)$
does not lie in
![]() $\mathbb{W}(\mathbb{Z}_{2})$
. This proves the claim.
$\mathbb{W}(\mathbb{Z}_{2})$
. This proves the claim.
Similarly, we extend the operator
![]() $F_{1}$
of
$F_{1}$
of
![]() $\hat{\mathscr{P}}_{\!\tilde{R}}$
to
$\hat{\mathscr{P}}_{\!\tilde{R}}$
to
![]() $\hat{\mathscr{P}}_{\!\tilde{R}}^{+}$
by
$\hat{\mathscr{P}}_{\!\tilde{R}}^{+}$
by
![]() $F_{1}=u_{0}^{-1}F_{1}^{+}$
. Then we have
$F_{1}=u_{0}^{-1}F_{1}^{+}$
. Then we have
![]() $c_{0}(F_{1}-1)=(F_{1}^{+}-1)c_{0}$
as homomorphisms
$c_{0}(F_{1}-1)=(F_{1}^{+}-1)c_{0}$
as homomorphisms
![]() $\hat{Q}_{\tilde{R}}^{+}\rightarrow \hat{P}_{\tilde{R}}^{+}$
, and it suffices to construct the desired diagram with
$\hat{Q}_{\tilde{R}}^{+}\rightarrow \hat{P}_{\tilde{R}}^{+}$
, and it suffices to construct the desired diagram with
![]() $F_{1}$
in place of
$F_{1}$
in place of
![]() $F_{1}^{+}$
. Now (5.4) implies that
$F_{1}^{+}$
. Now (5.4) implies that
![]() $\hat{Q}_{\tilde{R}}^{+}/\hat{Q}_{\tilde{R}}=\hat{P}_{\tilde{R}}^{+}/\hat{P}_{\tilde{R}}=\bar{P}_{\bar{k}}\cdot v(1)$
, which gives the exact rows. Clearly the left hand square of (5.3) commutes. The relation
$\hat{Q}_{\tilde{R}}^{+}/\hat{Q}_{\tilde{R}}=\hat{P}_{\tilde{R}}^{+}/\hat{P}_{\tilde{R}}=\bar{P}_{\bar{k}}\cdot v(1)$
, which gives the exact rows. Clearly the left hand square of (5.3) commutes. The relation
![]() $F_{1}(ax)=f_{1}(a)F(x)$
for
$F_{1}(ax)=f_{1}(a)F(x)$
for
![]() $x\in \hat{P}_{\tilde{R}}^{+}$
and
$x\in \hat{P}_{\tilde{R}}^{+}$
and
![]() $a\in \hat{\mathbb{I}}_{\tilde{R}}^{+}$
applied with
$a\in \hat{\mathbb{I}}_{\tilde{R}}^{+}$
applied with
![]() $a=v(1)$
, together with
$a=v(1)$
, together with
![]() $\bar{f}_{1}(v(1))=v(1)$
, shows that the right hand square of (5.3) commutes.◻
$\bar{f}_{1}(v(1))=v(1)$
, shows that the right hand square of (5.3) commutes.◻
Remark 5.2. The period isomorphisms
![]() $\operatorname{per}_{G}$
and
$\operatorname{per}_{G}$
and
![]() $\operatorname{per}_{G}^{+}$
are related by
$\operatorname{per}_{G}^{+}$
are related by
![]() $\operatorname{per}_{G}^{+}\circ i=\unicode[STIX]{x1D70F}_{c_{0}}\circ \operatorname{per}_{G}$
where
$\operatorname{per}_{G}^{+}\circ i=\unicode[STIX]{x1D70F}_{c_{0}}\circ \operatorname{per}_{G}$
where
![]() $i:T_{2}(G)\rightarrow T_{2}(G^{+})$
is the inclusion map and
$i:T_{2}(G)\rightarrow T_{2}(G^{+})$
is the inclusion map and
![]() $\unicode[STIX]{x1D70F}_{c_{0}}:T(\hat{\mathscr{P}}_{\!\tilde{R}})\rightarrow T(\hat{\mathscr{P}}_{\!\tilde{R}}^{+})$
is the homomorphism defined in (3.1).
$\unicode[STIX]{x1D70F}_{c_{0}}:T(\hat{\mathscr{P}}_{\!\tilde{R}})\rightarrow T(\hat{\mathscr{P}}_{\!\tilde{R}}^{+})$
is the homomorphism defined in (3.1).
6 The relation with
 $A_{\operatorname{cris}}$
$A_{\operatorname{cris}}$
Let
![]() $R$
be a complete discrete valuation ring with perfect residue field
$R$
be a complete discrete valuation ring with perfect residue field
![]() $k$
of characteristic
$k$
of characteristic
![]() $p$
and fraction field
$p$
and fraction field
![]() $K$
of characteristic zero. In this case the ring
$K$
of characteristic zero. In this case the ring
![]() $\tilde{R}^{\wedge }$
is equal to
$\tilde{R}^{\wedge }$
is equal to
![]() $\bar{R}^{\wedge }$
, the
$\bar{R}^{\wedge }$
, the
![]() $p$
-adic completion of the integral closure of
$p$
-adic completion of the integral closure of
![]() $R$
in
$R$
in
![]() $\bar{K}$
. Let
$\bar{K}$
. Let
![]() $A_{\operatorname{cris}}=A_{\operatorname{cris}}(\bar{R})$
, this is the
$A_{\operatorname{cris}}=A_{\operatorname{cris}}(\bar{R})$
, this is the
![]() $p$
-adic completion of the divided power envelope of the kernel of the canonical homomorphism
$p$
-adic completion of the divided power envelope of the kernel of the canonical homomorphism
![]() $\unicode[STIX]{x1D703}:A_{\inf }\rightarrow \bar{R}^{\wedge }$
, where
$\unicode[STIX]{x1D703}:A_{\inf }\rightarrow \bar{R}^{\wedge }$
, where
![]() $A_{\inf }=W({\mathcal{R}})$
, and where
$A_{\inf }=W({\mathcal{R}})$
, and where
![]() ${\mathcal{R}}$
is the projective limit of
${\mathcal{R}}$
is the projective limit of
![]() $\bar{R}/p\bar{R}$
under Frobenius. We have a frame
$\bar{R}/p\bar{R}$
under Frobenius. We have a frame
with
![]() $\unicode[STIX]{x1D70E}_{1}=p^{-1}\unicode[STIX]{x1D70E}$
. Footnote
2
$\unicode[STIX]{x1D70E}_{1}=p^{-1}\unicode[STIX]{x1D70E}$
. Footnote
2
For a
![]() $p$
-divisible group
$p$
-divisible group
![]() $G$
over
$G$
over
![]() $R$
let
$R$
let
![]() $\mathbb{D}(G)$
be its covariant Dieudonné crystal. The free
$\mathbb{D}(G)$
be its covariant Dieudonné crystal. The free
![]() $A_{\operatorname{cris}}$
-module
$A_{\operatorname{cris}}$
-module
![]() $M=\mathbb{D}(G_{\bar{R}^{\wedge }})_{A_{\operatorname{cris}}}$
carries a filtration
$M=\mathbb{D}(G_{\bar{R}^{\wedge }})_{A_{\operatorname{cris}}}$
carries a filtration
![]() $\operatorname{Fil}^{1}M$
and a
$\operatorname{Fil}^{1}M$
and a
![]() $\unicode[STIX]{x1D70E}$
-linear endomorphism
$\unicode[STIX]{x1D70E}$
-linear endomorphism
![]() $F$
. The operator
$F$
. The operator
![]() $F_{1}=p^{-1}F$
is well defined on
$F_{1}=p^{-1}F$
is well defined on
![]() $\operatorname{Fil}^{1}M$
, and we get an
$\operatorname{Fil}^{1}M$
, and we get an
![]() ${\mathcal{A}}_{\operatorname{cris}}$
-window
${\mathcal{A}}_{\operatorname{cris}}$
-window
![]() ${\mathcal{M}}=(M,\operatorname{Fil}^{1}M,F,F_{1})$
; see [Reference KisinKi1, Lemma A.2] or [Reference LauLa3, Proposition 3.17]. The window associated to
${\mathcal{M}}=(M,\operatorname{Fil}^{1}M,F,F_{1})$
; see [Reference KisinKi1, Lemma A.2] or [Reference LauLa3, Proposition 3.17]. The window associated to
![]() $\mathbb{Q}_{p}/\mathbb{Z}_{p}$
in this way is
$\mathbb{Q}_{p}/\mathbb{Z}_{p}$
in this way is
![]() ${\mathcal{A}}_{\operatorname{cris}}^{t}=(A_{\operatorname{cris}},A_{\operatorname{cris}},p\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70E})$
.
${\mathcal{A}}_{\operatorname{cris}}^{t}=(A_{\operatorname{cris}},A_{\operatorname{cris}},p\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70E})$
.
Following [Reference FaltingsFa, Section 6] one defines a period homomorphism
as follows. An element of
![]() $T_{p}(G)$
corresponds to a homomorphism
$T_{p}(G)$
corresponds to a homomorphism
![]() $\mathbb{Q}_{p}/\mathbb{Z}_{p}\rightarrow G$
over
$\mathbb{Q}_{p}/\mathbb{Z}_{p}\rightarrow G$
over
![]() $\bar{R}^{\wedge }$
, and the resulting map of
$\bar{R}^{\wedge }$
, and the resulting map of
![]() ${\mathcal{A}}_{\operatorname{cris}}$
-windows
${\mathcal{A}}_{\operatorname{cris}}$
-windows
![]() ${\mathcal{A}}_{\operatorname{cris}}^{t}\rightarrow {\mathcal{M}}$
corresponds to an element of
${\mathcal{A}}_{\operatorname{cris}}^{t}\rightarrow {\mathcal{M}}$
corresponds to an element of
![]() $T({\mathcal{M}})$
.Footnote
3
By [Reference FaltingsFa, Theorem 7],
$T({\mathcal{M}})$
.Footnote
3
By [Reference FaltingsFa, Theorem 7],
![]() $\operatorname{per}_{G,\operatorname{cris}}$
is bijective when
$\operatorname{per}_{G,\operatorname{cris}}$
is bijective when
![]() $p\geqslant 3$
, and injective with cokernel annihilated by
$p\geqslant 3$
, and injective with cokernel annihilated by
![]() $p$
when
$p$
when
![]() $p=2$
. More precisely, for
$p=2$
. More precisely, for
![]() $p=2$
the cokernel of
$p=2$
the cokernel of
![]() $\operatorname{per}_{G,\operatorname{cris}}$
is zero if
$\operatorname{per}_{G,\operatorname{cris}}$
is zero if
![]() $G$
is unipotent by [Reference KisinKi2, Proposition 1.1.10], but the cokernel is an
$G$
is unipotent by [Reference KisinKi2, Proposition 1.1.10], but the cokernel is an
![]() $\mathbb{F}_{2}$
-vector space of dimension equal to the height of
$\mathbb{F}_{2}$
-vector space of dimension equal to the height of
![]() $G$
if
$G$
if
![]() $G$
is of multiplicative type; this can be verified for the multiplicative group
$G$
is of multiplicative type; this can be verified for the multiplicative group
![]() $G=\unicode[STIX]{x1D707}_{p^{\infty }}$
and then follows from the fact that Fontaine’s element
$G=\unicode[STIX]{x1D707}_{p^{\infty }}$
and then follows from the fact that Fontaine’s element
![]() $t\in A_{\operatorname{cris}}$
satisfies
$t\in A_{\operatorname{cris}}$
satisfies
![]() $t^{p-1}\in pA_{\operatorname{cris}}$
; see [Reference FontaineFo2, (2.3.4)]. As in the proof of Proposition 5.1 it follows that for
$t^{p-1}\in pA_{\operatorname{cris}}$
; see [Reference FontaineFo2, (2.3.4)]. As in the proof of Proposition 5.1 it follows that for
![]() $p=2$
, the homomorphism
$p=2$
, the homomorphism
![]() $\operatorname{per}_{G,\operatorname{cris}}$
extends to an isomorphism
$\operatorname{per}_{G,\operatorname{cris}}$
extends to an isomorphism
![]() $T_{p}(G^{+})\cong T({\mathcal{M}})$
with
$T_{p}(G^{+})\cong T({\mathcal{M}})$
with
![]() $G^{+}$
as in Section 5.
$G^{+}$
as in Section 5.
We want to relate this with the period isomorphisms of Sections 4 and 5. For the sake of uniformity, for
![]() $p\geqslant 3$
we write
$p\geqslant 3$
we write
![]() $\mathbb{W}^{+}=\mathbb{W}$
etc. Then
$\mathbb{W}^{+}=\mathbb{W}$
etc. Then
![]() $\hat{\mathbb{W}}^{+}(\tilde{R})\rightarrow \bar{R}^{\wedge }$
is a divided power thickening of
$\hat{\mathbb{W}}^{+}(\tilde{R})\rightarrow \bar{R}^{\wedge }$
is a divided power thickening of
![]() $p$
-adic rings for every
$p$
-adic rings for every
![]() $p$
.
$p$
.
Lemma 6.1. There are unique homomorphisms
![]() $\unicode[STIX]{x1D718}_{\inf }$
and
$\unicode[STIX]{x1D718}_{\inf }$
and
![]() $\unicode[STIX]{x1D718}_{\operatorname{cris}}$
of thickenings of
$\unicode[STIX]{x1D718}_{\operatorname{cris}}$
of thickenings of
![]() $\bar{R}^{\wedge }$
as below. They commute with Frobenius, and the diagram commutes.
$\bar{R}^{\wedge }$
as below. They commute with Frobenius, and the diagram commutes.

Proof. Briefly said, the universal property of
![]() $A_{\operatorname{cris}}$
gives
$A_{\operatorname{cris}}$
gives
![]() $\unicode[STIX]{x1D718}_{\operatorname{cris}}$
, and the lemma explicates its construction. Namely, each
$\unicode[STIX]{x1D718}_{\operatorname{cris}}$
, and the lemma explicates its construction. Namely, each
![]() $x$
in the kernel of
$x$
in the kernel of
![]() $\hat{\mathbb{W}}^{+}(\tilde{R})/p^{n}\rightarrow \bar{R}^{\wedge }/p$
satisfies
$\hat{\mathbb{W}}^{+}(\tilde{R})/p^{n}\rightarrow \bar{R}^{\wedge }/p$
satisfies
![]() $x^{p^{n}}=0$
due to the divided powers on this ideal. Since the cokernel of the inclusion
$x^{p^{n}}=0$
due to the divided powers on this ideal. Since the cokernel of the inclusion
![]() $\hat{\mathbb{W}}(\tilde{R})\rightarrow \hat{\mathbb{W}}^{+}(\tilde{R})$
is the
$\hat{\mathbb{W}}(\tilde{R})\rightarrow \hat{\mathbb{W}}^{+}(\tilde{R})$
is the
![]() $\bar{k}$
-vector space with basis
$\bar{k}$
-vector space with basis
![]() $v(1)$
by (5.4), the kernel of
$v(1)$
by (5.4), the kernel of
![]() $\hat{\mathbb{W}}(\tilde{R})/p^{n}\rightarrow \hat{\mathbb{W}}^{+}(\tilde{R})/p^{n}$
is the
$\hat{\mathbb{W}}(\tilde{R})/p^{n}\rightarrow \hat{\mathbb{W}}^{+}(\tilde{R})/p^{n}$
is the
![]() $\bar{k}$
-vector space with basis
$\bar{k}$
-vector space with basis
![]() $p^{n}v(1)$
. Since
$p^{n}v(1)$
. Since
![]() $v(1)^{2}=pv(1)$
this kernel has square zero. Thus for each
$v(1)^{2}=pv(1)$
this kernel has square zero. Thus for each
![]() $x$
in the kernel of
$x$
in the kernel of
![]() $\hat{\mathbb{W}}(\tilde{R})/p^{n}\rightarrow \bar{R}^{\wedge }/p$
we have
$\hat{\mathbb{W}}(\tilde{R})/p^{n}\rightarrow \bar{R}^{\wedge }/p$
we have
![]() $x^{p^{n+1}}=0$
, and the universality of the Witt vectors (see for example [Reference LauLa3, Lemma 1.4]) gives a unique homomorphism
$x^{p^{n+1}}=0$
, and the universality of the Witt vectors (see for example [Reference LauLa3, Lemma 1.4]) gives a unique homomorphism
![]() $\unicode[STIX]{x1D718}_{\inf }$
of extensions of
$\unicode[STIX]{x1D718}_{\inf }$
of extensions of
![]() $\bar{R}^{\wedge }/p$
. The universality also implies that
$\bar{R}^{\wedge }/p$
. The universality also implies that
![]() $\unicode[STIX]{x1D718}_{\inf }$
commutes with the Frobenius and with the projections to
$\unicode[STIX]{x1D718}_{\inf }$
commutes with the Frobenius and with the projections to
![]() $\bar{R}^{\wedge }$
. Since
$\bar{R}^{\wedge }$
. Since
![]() $\hat{\mathbb{W}}^{+}(\tilde{R})\rightarrow \bar{R}^{\wedge }$
is a divided power extension of
$\hat{\mathbb{W}}^{+}(\tilde{R})\rightarrow \bar{R}^{\wedge }$
is a divided power extension of
![]() $p$
-adic rings,
$p$
-adic rings,
![]() $\unicode[STIX]{x1D718}_{\inf }$
extends uniquely to a homomorphism
$\unicode[STIX]{x1D718}_{\inf }$
extends uniquely to a homomorphism
![]() $\unicode[STIX]{x1D718}_{\operatorname{cris}}$
, and
$\unicode[STIX]{x1D718}_{\operatorname{cris}}$
, and
![]() $\unicode[STIX]{x1D718}_{\operatorname{cris}}$
commutes with the Frobenius because this holds for
$\unicode[STIX]{x1D718}_{\operatorname{cris}}$
commutes with the Frobenius because this holds for
![]() $\unicode[STIX]{x1D718}_{\inf }$
.◻
$\unicode[STIX]{x1D718}_{\inf }$
.◻
Since
![]() $\hat{\mathbb{W}}^{+}(\tilde{R})$
has no
$\hat{\mathbb{W}}^{+}(\tilde{R})$
has no
![]() $p$
-torsion it follows that
$p$
-torsion it follows that
![]() $\unicode[STIX]{x1D718}_{\operatorname{cris}}$
is a
$\unicode[STIX]{x1D718}_{\operatorname{cris}}$
is a
![]() $\tilde{{\mathcal{G}}}_{K}$
-equivariant strict frame homomorphism
$\tilde{{\mathcal{G}}}_{K}$
-equivariant strict frame homomorphism
For
![]() $G$
and
$G$
and
![]() ${\mathcal{M}}$
as above let
${\mathcal{M}}$
as above let
![]() $\mathscr{P}=\unicode[STIX]{x1D6F7}_{R}(G)$
be the Dieudonné display associated to
$\mathscr{P}=\unicode[STIX]{x1D6F7}_{R}(G)$
be the Dieudonné display associated to
![]() $G$
and let
$G$
and let
![]() $\unicode[STIX]{x1D6F7}_{R}^{+}(G)$
be its base change under the inclusion
$\unicode[STIX]{x1D6F7}_{R}^{+}(G)$
be its base change under the inclusion
![]() $\unicode[STIX]{x1D704}:\mathscr{D}_{R}\rightarrow \mathscr{D}_{R}^{+}$
, which is the identity when
$\unicode[STIX]{x1D704}:\mathscr{D}_{R}\rightarrow \mathscr{D}_{R}^{+}$
, which is the identity when
![]() $p\geqslant 3$
. The
$p\geqslant 3$
. The
![]() $\mathscr{D}_{R}^{+}$
-window
$\mathscr{D}_{R}^{+}$
-window
![]() $\unicode[STIX]{x1D6F7}_{R}^{+}(G)$
can be defined by evaluating the crystal
$\unicode[STIX]{x1D6F7}_{R}^{+}(G)$
can be defined by evaluating the crystal
![]() $\mathbb{D}(G)$
at
$\mathbb{D}(G)$
at
![]() $\mathbb{W}^{+}(R)$
; see [Reference LauLa3, Theorem 3.19] if
$\mathbb{W}^{+}(R)$
; see [Reference LauLa3, Theorem 3.19] if
![]() $p\geqslant 3$
and [Reference LauLa3, Proposition 3.24 & Theorem 4.9] if
$p\geqslant 3$
and [Reference LauLa3, Proposition 3.24 & Theorem 4.9] if
![]() $p=2$
. By the functoriality of
$p=2$
. By the functoriality of
![]() $\mathbb{D}(G)$
we get an isomorphism
$\mathbb{D}(G)$
we get an isomorphism
![]() $\hat{\mathscr{P}}_{\tilde{R}}^{+}\cong \unicode[STIX]{x1D718}_{\operatorname{cris}\ast }({\mathcal{M}})$
of
$\hat{\mathscr{P}}_{\tilde{R}}^{+}\cong \unicode[STIX]{x1D718}_{\operatorname{cris}\ast }({\mathcal{M}})$
of
![]() $\hat{\mathscr{D}}_{\tilde{R}}^{+}$
-windows, which induces a homomorphism of
$\hat{\mathscr{D}}_{\tilde{R}}^{+}$
-windows, which induces a homomorphism of
![]() ${\mathcal{G}}_{K}$
-modules
${\mathcal{G}}_{K}$
-modules
as defined in (3.1) with
![]() $c=1$
.
$c=1$
.
Proposition 6.2. The following diagram of
![]() ${\mathcal{G}}_{K}$
-modules commutes, and
${\mathcal{G}}_{K}$
-modules commutes, and
![]() $\unicode[STIX]{x1D70F}$
is an isomorphism.
$\unicode[STIX]{x1D70F}$
is an isomorphism.

Proof of Proposition 6.2.
The composition
![]() $\unicode[STIX]{x1D70F}_{c_{0}}\circ \operatorname{per}_{G}$
extends to an isomorphism
$\unicode[STIX]{x1D70F}_{c_{0}}\circ \operatorname{per}_{G}$
extends to an isomorphism
![]() $T_{p}(G^{+})\cong T(\hat{\mathscr{P}}_{\tilde{R}}^{+})$
by Proposition 5.1 and Remark 5.2. Thus if the diagram commutes, by the properties of
$T_{p}(G^{+})\cong T(\hat{\mathscr{P}}_{\tilde{R}}^{+})$
by Proposition 5.1 and Remark 5.2. Thus if the diagram commutes, by the properties of
![]() $\operatorname{per}_{G,\operatorname{cris}}$
recalled above it follows that
$\operatorname{per}_{G,\operatorname{cris}}$
recalled above it follows that
![]() $\unicode[STIX]{x1D70F}$
is an isomorphism. Let us prove that the diagram commutes.
$\unicode[STIX]{x1D70F}$
is an isomorphism. Let us prove that the diagram commutes.
We start with the case
![]() $G=\mathbb{Q}_{p}/\mathbb{Z}_{p}$
. Then
$G=\mathbb{Q}_{p}/\mathbb{Z}_{p}$
. Then
![]() $T_{p}(G)=\mathbb{Z}_{p}$
. By Remark 4.2, the associated windows can be identified as
$T_{p}(G)=\mathbb{Z}_{p}$
. By Remark 4.2, the associated windows can be identified as
![]() $\mathscr{P}=(\mathbb{W}(R),\mathbb{W}(R),pu_{0}f,f)$
and
$\mathscr{P}=(\mathbb{W}(R),\mathbb{W}(R),pu_{0}f,f)$
and
![]() $\mathscr{P}^{+}=(\mathbb{W}^{+}(R),\mathbb{W}^{+}(R),pf,f)$
and
$\mathscr{P}^{+}=(\mathbb{W}^{+}(R),\mathbb{W}^{+}(R),pf,f)$
and
![]() ${\mathcal{M}}=(A_{\operatorname{cris}},A_{\operatorname{cris}},p\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70E})$
. The three modules
${\mathcal{M}}=(A_{\operatorname{cris}},A_{\operatorname{cris}},p\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70E})$
. The three modules
![]() $T({\mathcal{M}})=A_{\operatorname{cris}}^{\unicode[STIX]{x1D70E}=1}$
and
$T({\mathcal{M}})=A_{\operatorname{cris}}^{\unicode[STIX]{x1D70E}=1}$
and
![]() $T(\hat{\mathscr{P}}_{\tilde{R}})=\hat{\mathbb{W}}(\tilde{R})^{f=1}$
and
$T(\hat{\mathscr{P}}_{\tilde{R}})=\hat{\mathbb{W}}(\tilde{R})^{f=1}$
and
![]() $T(\hat{\mathscr{P}}_{\tilde{R}}^{+})=\hat{\mathbb{W}}^{+}(\tilde{R})^{f=1}$
are then all identified with
$T(\hat{\mathscr{P}}_{\tilde{R}}^{+})=\hat{\mathbb{W}}^{+}(\tilde{R})^{f=1}$
are then all identified with
![]() $\mathbb{Z}_{p}$
; see Lemma 4.3. Under these identifications, the three arrows
$\mathbb{Z}_{p}$
; see Lemma 4.3. Under these identifications, the three arrows
![]() $\unicode[STIX]{x1D70F}$
and
$\unicode[STIX]{x1D70F}$
and
![]() $\operatorname{per}_{G,\operatorname{cris}}$
and
$\operatorname{per}_{G,\operatorname{cris}}$
and
![]() $\operatorname{per}_{G}$
are the identity of
$\operatorname{per}_{G}$
are the identity of
![]() $\mathbb{Z}_{p}$
; see Remark 4.2. The base change
$\mathbb{Z}_{p}$
; see Remark 4.2. The base change
![]() $\unicode[STIX]{x1D704}_{\ast }(\mathscr{P})$
is equal to
$\unicode[STIX]{x1D704}_{\ast }(\mathscr{P})$
is equal to
![]() $(\mathbb{W}^{+}(R),\mathbb{W}^{+}(R),pu_{0}f,u_{0}f)$
, and the implicit isomorphism
$(\mathbb{W}^{+}(R),\mathbb{W}^{+}(R),pu_{0}f,u_{0}f)$
, and the implicit isomorphism
![]() $\unicode[STIX]{x1D704}_{\ast }(\mathscr{P})\cong \mathscr{P}^{+}$
is necessarily given by multiplication with the unique unit
$\unicode[STIX]{x1D704}_{\ast }(\mathscr{P})\cong \mathscr{P}^{+}$
is necessarily given by multiplication with the unique unit
![]() $c\in \mathbb{W}^{+}(\mathbb{Z}_{p})$
with
$c\in \mathbb{W}^{+}(\mathbb{Z}_{p})$
with
![]() $cu_{0}=f(c)$
which maps to
$cu_{0}=f(c)$
which maps to
![]() $1$
in
$1$
in
![]() $W(\mathbb{F}_{p})$
, namely
$W(\mathbb{F}_{p})$
, namely
![]() $c=c_{0}^{-1}$
. Thus under the chosen identifications,
$c=c_{0}^{-1}$
. Thus under the chosen identifications,
![]() $\unicode[STIX]{x1D70F}_{c_{0}}=c_{0}c_{0}^{-1}$
is the identity as well, and the diagram commutes for
$\unicode[STIX]{x1D70F}_{c_{0}}=c_{0}c_{0}^{-1}$
is the identity as well, and the diagram commutes for
![]() $\mathbb{Q}_{p}/\mathbb{Z}_{p}$
.
$\mathbb{Q}_{p}/\mathbb{Z}_{p}$
.
Let now
![]() $G$
be arbitrary. Since the map
$G$
be arbitrary. Since the map
![]() $\unicode[STIX]{x1D70F}_{c_{0}}\circ \operatorname{per}_{G}=\operatorname{per}_{G}^{+}$
is injective with cokernel annihilated by
$\unicode[STIX]{x1D70F}_{c_{0}}\circ \operatorname{per}_{G}=\operatorname{per}_{G}^{+}$
is injective with cokernel annihilated by
![]() $p$
, the composition
$p$
, the composition
![]() $\unicode[STIX]{x1D6FE}=p\cdot (\operatorname{per}_{G}^{+})^{-1}\circ \unicode[STIX]{x1D70F}\circ \operatorname{per}_{G,\operatorname{cris}}$
is a well-defined functorial endomorphism of
$\unicode[STIX]{x1D6FE}=p\cdot (\operatorname{per}_{G}^{+})^{-1}\circ \unicode[STIX]{x1D70F}\circ \operatorname{per}_{G,\operatorname{cris}}$
is a well-defined functorial endomorphism of
![]() $T_{p}G$
. We have to show that
$T_{p}G$
. We have to show that
![]() $\unicode[STIX]{x1D6FE}=p$
. By [Reference TateTa, Corollary 1],
$\unicode[STIX]{x1D6FE}=p$
. By [Reference TateTa, Corollary 1],
![]() $\unicode[STIX]{x1D6FE}$
comes from an endomorphism
$\unicode[STIX]{x1D6FE}$
comes from an endomorphism
![]() $\unicode[STIX]{x1D6FE}_{G}$
of
$\unicode[STIX]{x1D6FE}_{G}$
of
![]() $G$
; moreover
$G$
; moreover
![]() $\unicode[STIX]{x1D6FE}_{G}$
is functorial in
$\unicode[STIX]{x1D6FE}_{G}$
is functorial in
![]() $G$
and compatible with normal finite extensions of the base ring
$G$
and compatible with normal finite extensions of the base ring
![]() $R$
inside
$R$
inside
![]() $\bar{K}$
. The endomorphisms
$\bar{K}$
. The endomorphisms
![]() $\unicode[STIX]{x1D6FE}_{G}$
induce a functorial endomorphism
$\unicode[STIX]{x1D6FE}_{G}$
induce a functorial endomorphism
![]() $\unicode[STIX]{x1D6FE}_{H}$
of each commutative finite flat
$\unicode[STIX]{x1D6FE}_{H}$
of each commutative finite flat
![]() $p$
-group scheme
$p$
-group scheme
![]() $H$
over a normal finite extension
$H$
over a normal finite extension
![]() $R^{\prime }$
of
$R^{\prime }$
of
![]() $R$
inside
$R$
inside
![]() $\bar{K}$
because
$\bar{K}$
because
![]() $H$
can be embedded into a
$H$
can be embedded into a
![]() $p$
-divisible group
$p$
-divisible group
![]() $G$
by Raynaud [Reference Berthelot, Breen and MessingBBM, Theorem 3.1.1], and the quotient
$G$
by Raynaud [Reference Berthelot, Breen and MessingBBM, Theorem 3.1.1], and the quotient
![]() $G/H$
is a
$G/H$
is a
![]() $p$
-divisible group, so
$p$
-divisible group, so
![]() $\unicode[STIX]{x1D6FE}_{G}$
induces
$\unicode[STIX]{x1D6FE}_{G}$
induces
![]() $\unicode[STIX]{x1D6FE}_{H}$
; cf. the proof of [Reference KisinKi1, Theorem 2.3.5] or [Reference LauLa3, Proposition 8.1]. Assume that
$\unicode[STIX]{x1D6FE}_{H}$
; cf. the proof of [Reference KisinKi1, Theorem 2.3.5] or [Reference LauLa3, Proposition 8.1]. Assume that
![]() $H$
is annihilated by
$H$
is annihilated by
![]() $p^{r}$
and let
$p^{r}$
and let
![]() $H_{0}=\mathbb{Z}/p^{r}\mathbb{Z}$
. There is a normal finite extension
$H_{0}=\mathbb{Z}/p^{r}\mathbb{Z}$
. There is a normal finite extension
![]() $R^{\prime \prime }$
of
$R^{\prime \prime }$
of
![]() $R^{\prime }$
inside
$R^{\prime }$
inside
![]() $\bar{K}$
such that
$\bar{K}$
such that
![]() $H(\bar{K})=H(R^{\prime \prime })=\operatorname{Hom}_{R^{\prime \prime }}(H_{0},H)$
. Since
$H(\bar{K})=H(R^{\prime \prime })=\operatorname{Hom}_{R^{\prime \prime }}(H_{0},H)$
. Since
![]() $\unicode[STIX]{x1D6FE}_{H_{0}}=p$
it follows that
$\unicode[STIX]{x1D6FE}_{H_{0}}=p$
it follows that
![]() $\unicode[STIX]{x1D6FE}_{H}=p$
, and thus
$\unicode[STIX]{x1D6FE}_{H}=p$
, and thus
![]() $\unicode[STIX]{x1D6FE}_{G}=p$
for all
$\unicode[STIX]{x1D6FE}_{G}=p$
for all
![]() $G$
.◻
$G$
.◻
7 The ring
 $\mathfrak{S}^{\operatorname{nr}}$
$\mathfrak{S}^{\operatorname{nr}}$
Let us recall the ring
![]() $\mathfrak{S}^{\operatorname{nr}}$
of [Reference KisinKi1], which is denoted by
$\mathfrak{S}^{\operatorname{nr}}$
of [Reference KisinKi1], which is denoted by
![]() $A_{S}^{+}$
in [Reference FontaineFo1]. One starts with a two-dimensional complete regular local ring
$A_{S}^{+}$
in [Reference FontaineFo1]. One starts with a two-dimensional complete regular local ring
![]() $\mathfrak{S}$
of characteristic zero with perfect residue field
$\mathfrak{S}$
of characteristic zero with perfect residue field
![]() $k$
of characteristic
$k$
of characteristic
![]() $p$
equipped with a Frobenius lift
$p$
equipped with a Frobenius lift
![]() $\unicode[STIX]{x1D70E}:\mathfrak{S}\rightarrow \mathfrak{S}$
.
$\unicode[STIX]{x1D70E}:\mathfrak{S}\rightarrow \mathfrak{S}$
.
There is a unique ring homomorphism
![]() $\unicode[STIX]{x1D6E5}:\mathfrak{S}\rightarrow W(\mathfrak{S})$
with
$\unicode[STIX]{x1D6E5}:\mathfrak{S}\rightarrow W(\mathfrak{S})$
with
![]() $w_{n}\circ \unicode[STIX]{x1D6E5}=\unicode[STIX]{x1D70E}^{n}$
where
$w_{n}\circ \unicode[STIX]{x1D6E5}=\unicode[STIX]{x1D70E}^{n}$
where
![]() $w_{n}$
is the
$w_{n}$
is the
![]() $n$
th Witt polynomial, and then
$n$
th Witt polynomial, and then
![]() $\unicode[STIX]{x1D6E5}\circ \unicode[STIX]{x1D70E}=f\circ \unicode[STIX]{x1D6E5}$
; see [Reference LazardLaz, Chapter VII, Proposition 4.12]. The composition
$\unicode[STIX]{x1D6E5}\circ \unicode[STIX]{x1D70E}=f\circ \unicode[STIX]{x1D6E5}$
; see [Reference LazardLaz, Chapter VII, Proposition 4.12]. The composition
![]() $\mathfrak{S}\rightarrow W(\mathfrak{S})\rightarrow W(k)$
is surjective, which implies that
$\mathfrak{S}\rightarrow W(\mathfrak{S})\rightarrow W(k)$
is surjective, which implies that
![]() $p\not \in \mathfrak{m}_{\mathfrak{S}}^{2}$
. Let
$p\not \in \mathfrak{m}_{\mathfrak{S}}^{2}$
. Let
![]() $t\in \mathfrak{m}_{\mathfrak{S}}\setminus \mathfrak{m}_{\mathfrak{S}}^{2}$
map to zero in
$t\in \mathfrak{m}_{\mathfrak{S}}\setminus \mathfrak{m}_{\mathfrak{S}}^{2}$
map to zero in
![]() $W(k)$
. Then
$W(k)$
. Then
![]() $\mathfrak{S}=W(k)[[t]]$
and
$\mathfrak{S}=W(k)[[t]]$
and
![]() $t$
generates the kernel of
$t$
generates the kernel of
![]() $\mathfrak{S}\rightarrow W(k)$
, in particular
$\mathfrak{S}\rightarrow W(k)$
, in particular
![]() $\unicode[STIX]{x1D70E}(t)\in t\mathfrak{S}$
.
$\unicode[STIX]{x1D70E}(t)\in t\mathfrak{S}$
.
Let
![]() ${\mathcal{O}}_{{\mathcal{E}}}$
be the
${\mathcal{O}}_{{\mathcal{E}}}$
be the
![]() $p$
-adic completion of
$p$
-adic completion of
![]() $\mathfrak{S}[t^{-1}]$
and let
$\mathfrak{S}[t^{-1}]$
and let
![]() $\mathbb{E}=k((t))$
be its residue field. Fix a maximal unramified extension
$\mathbb{E}=k((t))$
be its residue field. Fix a maximal unramified extension
![]() ${\mathcal{O}}_{{\mathcal{E}}^{\operatorname{nr}}}$
of
${\mathcal{O}}_{{\mathcal{E}}^{\operatorname{nr}}}$
of
![]() ${\mathcal{O}}_{{\mathcal{E}}}$
and let
${\mathcal{O}}_{{\mathcal{E}}}$
and let
![]() ${\mathcal{O}}_{\widehat{{\mathcal{E}}^{\operatorname{nr}}}}$
be its
${\mathcal{O}}_{\widehat{{\mathcal{E}}^{\operatorname{nr}}}}$
be its
![]() $p$
-adic completion. Let
$p$
-adic completion. Let
![]() $\mathbb{E}^{\operatorname{sep}}$
be the residue field of
$\mathbb{E}^{\operatorname{sep}}$
be the residue field of
![]() ${\mathcal{O}}_{{\mathcal{E}}^{\operatorname{nr}}}$
, let
${\mathcal{O}}_{{\mathcal{E}}^{\operatorname{nr}}}$
, let
![]() $\bar{\mathbb{E}}$
be an algebraic closure of
$\bar{\mathbb{E}}$
be an algebraic closure of
![]() $\mathbb{E}^{\operatorname{sep}}$
, let
$\mathbb{E}^{\operatorname{sep}}$
, let
![]() ${\mathcal{O}}_{\mathbb{E}}=\mathfrak{S}/p\mathfrak{S}=k[[t]]$
, and let
${\mathcal{O}}_{\mathbb{E}}=\mathfrak{S}/p\mathfrak{S}=k[[t]]$
, and let
![]() ${\mathcal{O}}_{\bar{\mathbb{E}}}\subset \bar{\mathbb{E}}$
be its integral closure. The Frobenius lift
${\mathcal{O}}_{\bar{\mathbb{E}}}\subset \bar{\mathbb{E}}$
be its integral closure. The Frobenius lift
![]() $\unicode[STIX]{x1D70E}$
on
$\unicode[STIX]{x1D70E}$
on
![]() $\mathfrak{S}$
extends uniquely to
$\mathfrak{S}$
extends uniquely to
![]() ${\mathcal{O}}_{\widehat{{\mathcal{E}}^{\operatorname{nr}}}}$
and induces a homomorphism
${\mathcal{O}}_{\widehat{{\mathcal{E}}^{\operatorname{nr}}}}$
and induces a homomorphism
with
![]() $\unicode[STIX]{x1D6E5}$
as above. (7.1) is injective since both sides are discrete valuation rings with prime element
$\unicode[STIX]{x1D6E5}$
as above. (7.1) is injective since both sides are discrete valuation rings with prime element
![]() $p$
, and the reduction modulo
$p$
, and the reduction modulo
![]() $p$
is injective. One defines
$p$
is injective. One defines
![]() $\mathfrak{S}^{\operatorname{nr}}={\mathcal{O}}_{\widehat{{\mathcal{E}}^{\operatorname{nr}}}}\cap W({\mathcal{O}}_{\bar{\mathbb{E}}})$
inside
$\mathfrak{S}^{\operatorname{nr}}={\mathcal{O}}_{\widehat{{\mathcal{E}}^{\operatorname{nr}}}}\cap W({\mathcal{O}}_{\bar{\mathbb{E}}})$
inside
![]() $W(\bar{\mathbb{E}})$
. This ring is stable under
$W(\bar{\mathbb{E}})$
. This ring is stable under
![]() $\unicode[STIX]{x1D70E}$
, and
$\unicode[STIX]{x1D70E}$
, and
![]() $\mathfrak{S}^{\operatorname{nr}}=\varprojlim \mathfrak{S}_{n}^{\operatorname{nr}}$
with
$\mathfrak{S}^{\operatorname{nr}}=\varprojlim \mathfrak{S}_{n}^{\operatorname{nr}}$
with
![]() $\mathfrak{S}_{n}^{\operatorname{nr}}=({\mathcal{O}}_{{\mathcal{E}}^{\operatorname{nr}}}/p^{n}{\mathcal{O}}_{{\mathcal{E}}^{\operatorname{nr}}})\cap W_{n}({\mathcal{O}}_{\bar{\mathbb{E}}})$
inside
$\mathfrak{S}_{n}^{\operatorname{nr}}=({\mathcal{O}}_{{\mathcal{E}}^{\operatorname{nr}}}/p^{n}{\mathcal{O}}_{{\mathcal{E}}^{\operatorname{nr}}})\cap W_{n}({\mathcal{O}}_{\bar{\mathbb{E}}})$
inside
![]() $\mathbb{W}_{n}(\bar{\mathbb{E}})$
. By [Reference FontaineFo1, B 1.8.3] we have
$\mathbb{W}_{n}(\bar{\mathbb{E}})$
. By [Reference FontaineFo1, B 1.8.3] we have
![]() $\mathfrak{S}_{n}^{\operatorname{nr}}=\mathfrak{S}^{\operatorname{nr}}/p^{n}\mathfrak{S}^{\operatorname{nr}}$
, in particular
$\mathfrak{S}_{n}^{\operatorname{nr}}=\mathfrak{S}^{\operatorname{nr}}/p^{n}\mathfrak{S}^{\operatorname{nr}}$
, in particular
![]() $\mathfrak{S}^{\operatorname{nr}}$
is
$\mathfrak{S}^{\operatorname{nr}}$
is
![]() $p$
-adically complete.
$p$
-adically complete.
8 Breuil–Kisin modules
Let
![]() $R$
be a complete discrete valuation ring with perfect residue field
$R$
be a complete discrete valuation ring with perfect residue field
![]() $k$
of characteristic
$k$
of characteristic
![]() $p$
and fraction field
$p$
and fraction field
![]() $K$
of characteristic zero. We recall briefly the classification of commutative finite flat
$K$
of characteristic zero. We recall briefly the classification of commutative finite flat
![]() $p$
-group schemes over
$p$
-group schemes over
![]() $R$
following [Reference LauLa3]; see the introduction for a brief discussion of the history of this result.
$R$
following [Reference LauLa3]; see the introduction for a brief discussion of the history of this result.
Let
![]() $\mathfrak{S}=W(k)[[t]]$
and let
$\mathfrak{S}=W(k)[[t]]$
and let
![]() $\unicode[STIX]{x1D70E}:\mathfrak{S}\rightarrow \mathfrak{S}$
be a Frobenius lift that stabilizes the ideal
$\unicode[STIX]{x1D70E}:\mathfrak{S}\rightarrow \mathfrak{S}$
be a Frobenius lift that stabilizes the ideal
![]() $t\mathfrak{S}$
. We choose a presentation
$t\mathfrak{S}$
. We choose a presentation
![]() $R=\mathfrak{S}/E\mathfrak{S}$
where
$R=\mathfrak{S}/E\mathfrak{S}$
where
![]() $E$
has constant term
$E$
has constant term
![]() $p$
. Let
$p$
. Let
![]() $\unicode[STIX]{x1D70B}\in R$
be the image of
$\unicode[STIX]{x1D70B}\in R$
be the image of
![]() $t$
, so
$t$
, so
![]() $\unicode[STIX]{x1D70B}$
generates the maximal ideal of
$\unicode[STIX]{x1D70B}$
generates the maximal ideal of
![]() $R$
.
$R$
.
For an
![]() $\mathfrak{S}$
-module
$\mathfrak{S}$
-module
![]() $M$
let
$M$
let
![]() $M^{(\unicode[STIX]{x1D70E})}=\mathfrak{S}\otimes _{\unicode[STIX]{x1D70E},\mathfrak{S}}M$
. We consider pairs
$M^{(\unicode[STIX]{x1D70E})}=\mathfrak{S}\otimes _{\unicode[STIX]{x1D70E},\mathfrak{S}}M$
. We consider pairs
![]() $(M,\unicode[STIX]{x1D719})$
where
$(M,\unicode[STIX]{x1D719})$
where
![]() $M$
is an
$M$
is an
![]() $\mathfrak{S}$
-module of finite type and where
$\mathfrak{S}$
-module of finite type and where
![]() $\unicode[STIX]{x1D719}:M\rightarrow M^{(\unicode[STIX]{x1D70E})}$
is an
$\unicode[STIX]{x1D719}:M\rightarrow M^{(\unicode[STIX]{x1D70E})}$
is an
![]() $\mathfrak{S}$
-linear map with cokernel annihilated by
$\mathfrak{S}$
-linear map with cokernel annihilated by
![]() $E$
. Following the [Reference Vasiu and ZinkVZ] terminology,
$E$
. Following the [Reference Vasiu and ZinkVZ] terminology,
![]() $(M,\unicode[STIX]{x1D719})$
is called a Breuil window (respectively a Breuil module) relative to
$(M,\unicode[STIX]{x1D719})$
is called a Breuil window (respectively a Breuil module) relative to
![]() $\mathfrak{S}\rightarrow R$
if the
$\mathfrak{S}\rightarrow R$
if the
![]() $\mathfrak{S}$
-module
$\mathfrak{S}$
-module
![]() $M$
is free (respectively annihilated by a power of
$M$
is free (respectively annihilated by a power of
![]() $p$
and of projective dimension at most one).
$p$
and of projective dimension at most one).
We have a frame in the sense of [Reference LauLa2]
with
![]() $\unicode[STIX]{x1D70E}_{1}(Ex)=\unicode[STIX]{x1D70E}(x)$
for
$\unicode[STIX]{x1D70E}_{1}(Ex)=\unicode[STIX]{x1D70E}(x)$
for
![]() $x\in \mathfrak{S}$
. Windows
$x\in \mathfrak{S}$
. Windows
![]() $\mathscr{P}=(P,Q,F,F_{1})$
over
$\mathscr{P}=(P,Q,F,F_{1})$
over
![]() $\mathscr{B}$
are equivalent to Breuil windows relative to
$\mathscr{B}$
are equivalent to Breuil windows relative to
![]() $\mathfrak{S}\rightarrow R$
by the functor
$\mathfrak{S}\rightarrow R$
by the functor
![]() $\mathscr{P}\mapsto (Q,\unicode[STIX]{x1D719})$
where
$\mathscr{P}\mapsto (Q,\unicode[STIX]{x1D719})$
where
![]() $\unicode[STIX]{x1D719}:Q\rightarrow Q^{(\unicode[STIX]{x1D70E})}$
is the composition of the inclusion
$\unicode[STIX]{x1D719}:Q\rightarrow Q^{(\unicode[STIX]{x1D70E})}$
is the composition of the inclusion
![]() $Q\rightarrow P$
with the inverse of the isomorphism
$Q\rightarrow P$
with the inverse of the isomorphism
![]() $Q^{(\unicode[STIX]{x1D70E})}\cong P$
defined by
$Q^{(\unicode[STIX]{x1D70E})}\cong P$
defined by
![]() $a\otimes x\mapsto aF_{1}(x)$
; the inverse functor maps
$a\otimes x\mapsto aF_{1}(x)$
; the inverse functor maps
![]() $(Q,\unicode[STIX]{x1D719})$
to
$(Q,\unicode[STIX]{x1D719})$
to
![]() $(P,Q,F,F_{1})$
with
$(P,Q,F,F_{1})$
with
![]() $P=Q^{(\unicode[STIX]{x1D70E})}$
such that the inclusion
$P=Q^{(\unicode[STIX]{x1D70E})}$
such that the inclusion
![]() $Q\rightarrow P$
is
$Q\rightarrow P$
is
![]() $\unicode[STIX]{x1D719}$
and
$\unicode[STIX]{x1D719}$
and
![]() $F_{1}:Q\rightarrow P$
is
$F_{1}:Q\rightarrow P$
is
![]() $x\mapsto 1\otimes x$
, which also gives
$x\mapsto 1\otimes x$
, which also gives
![]() $F(x)=F_{1}(Ex)$
; see [Reference LauLa2, Lemma 8.2].
$F(x)=F_{1}(Ex)$
; see [Reference LauLa2, Lemma 8.2].
As in [Reference LauLa3, Section 6] let
![]() $\unicode[STIX]{x1D718}$
be the ring homomorphism
$\unicode[STIX]{x1D718}$
be the ring homomorphism
Its image lies in
![]() $\mathbb{W}(R)$
if and only if the endomorphism of
$\mathbb{W}(R)$
if and only if the endomorphism of
![]() $t\mathfrak{S}/t^{2}\mathfrak{S}$
induced by
$t\mathfrak{S}/t^{2}\mathfrak{S}$
induced by
![]() $\unicode[STIX]{x1D70E}$
is divisible by
$\unicode[STIX]{x1D70E}$
is divisible by
![]() $p^{2}$
. In this case,
$p^{2}$
. In this case,
![]() $\unicode[STIX]{x1D718}:\mathfrak{S}\rightarrow \mathbb{W}(R)$
is a
$\unicode[STIX]{x1D718}:\mathfrak{S}\rightarrow \mathbb{W}(R)$
is a
![]() $u$
-homomorphism of frames
$u$
-homomorphism of frames
![]() $\mathscr{B}\rightarrow \mathscr{D}_{R}$
for the unit
$\mathscr{B}\rightarrow \mathscr{D}_{R}$
for the unit
![]() $u=f_{1}(\unicode[STIX]{x1D718}(E))$
of
$u=f_{1}(\unicode[STIX]{x1D718}(E))$
of
![]() $\mathbb{W}(R)$
, and
$\mathbb{W}(R)$
, and
![]() $\unicode[STIX]{x1D718}$
induces an equivalence between
$\unicode[STIX]{x1D718}$
induces an equivalence between
![]() $\mathscr{B}$
-windows and
$\mathscr{B}$
-windows and
![]() $\mathscr{D}_{R}$
-windows, which are equivalent to
$\mathscr{D}_{R}$
-windows, which are equivalent to
![]() $p$
-divisible groups over
$p$
-divisible groups over
![]() $R$
. As a consequence, Breuil modules relative to
$R$
. As a consequence, Breuil modules relative to
![]() $\mathfrak{S}\rightarrow R$
are equivalent to commutative finite flat
$\mathfrak{S}\rightarrow R$
are equivalent to commutative finite flat
![]() $p$
-group schemes over
$p$
-group schemes over
![]() $R$
; see [Reference LauLa3, Corollary 6.8].
$R$
; see [Reference LauLa3, Corollary 6.8].
Since
![]() $u$
maps to
$u$
maps to
![]() $1$
under
$1$
under
![]() $\mathbb{W}(R)\rightarrow W(k)$
, there is a unique invertible element
$\mathbb{W}(R)\rightarrow W(k)$
, there is a unique invertible element
![]() $c\in \mathbb{W}(R)$
which maps to
$c\in \mathbb{W}(R)$
which maps to
![]() $1$
in
$1$
in
![]() $W(k)$
with
$W(k)$
with
![]() $c\unicode[STIX]{x1D70E}(c^{-1})=u$
. It is given by
$c\unicode[STIX]{x1D70E}(c^{-1})=u$
. It is given by
![]() $c=u\unicode[STIX]{x1D70E}(u)\unicode[STIX]{x1D70E}^{2}(u)\cdots \,$
; see the proof of [Reference LauLa2, Proposition 8.7].
$c=u\unicode[STIX]{x1D70E}(u)\unicode[STIX]{x1D70E}^{2}(u)\cdots \,$
; see the proof of [Reference LauLa2, Proposition 8.7].
8.1 Modules of invariants
For a Breuil module or Breuil window
![]() $(M,\unicode[STIX]{x1D719})$
relative to
$(M,\unicode[STIX]{x1D719})$
relative to
![]() $\mathfrak{S}\rightarrow R$
we write
$\mathfrak{S}\rightarrow R$
we write
![]() $M^{\operatorname{nr}}=\mathfrak{S}^{\operatorname{nr}}\otimes _{\mathfrak{S}}M$
and
$M^{\operatorname{nr}}=\mathfrak{S}^{\operatorname{nr}}\otimes _{\mathfrak{S}}M$
and
![]() $M_{{\mathcal{E}}}^{\operatorname{nr}}={\mathcal{O}}_{\widehat{{\mathcal{E}}^{\operatorname{nr}}}}\otimes _{\mathfrak{S}}M$
and define
$M_{{\mathcal{E}}}^{\operatorname{nr}}={\mathcal{O}}_{\widehat{{\mathcal{E}}^{\operatorname{nr}}}}\otimes _{\mathfrak{S}}M$
and define
For reference we record the following consequence of some results of [Reference FontaineFo1].
Lemma 8.1. The
![]() $\mathbb{Z}_{p}$
-module
$\mathbb{Z}_{p}$
-module
![]() $T_{{\mathcal{E}}}^{\operatorname{nr}}(M,\unicode[STIX]{x1D719})$
is finitely generated, and the natural map
$T_{{\mathcal{E}}}^{\operatorname{nr}}(M,\unicode[STIX]{x1D719})$
is finitely generated, and the natural map
is bijective. The natural map
is bijective as well.
Proof. The homomorphism
![]() $\unicode[STIX]{x1D719}:M_{{\mathcal{E}}}^{\operatorname{nr}}\rightarrow (M_{{\mathcal{E}}}^{\operatorname{nr}})^{(\unicode[STIX]{x1D70E})}$
is bijective. If
$\unicode[STIX]{x1D719}:M_{{\mathcal{E}}}^{\operatorname{nr}}\rightarrow (M_{{\mathcal{E}}}^{\operatorname{nr}})^{(\unicode[STIX]{x1D70E})}$
is bijective. If
![]() $\unicode[STIX]{x1D713}:M_{{\mathcal{E}}}^{\operatorname{nr}}\rightarrow M_{{\mathcal{E}}}^{\operatorname{nr}}$
is the
$\unicode[STIX]{x1D713}:M_{{\mathcal{E}}}^{\operatorname{nr}}\rightarrow M_{{\mathcal{E}}}^{\operatorname{nr}}$
is the
![]() $\unicode[STIX]{x1D70E}$
-linear map whose linearization is the inverse of
$\unicode[STIX]{x1D70E}$
-linear map whose linearization is the inverse of
![]() $\unicode[STIX]{x1D719}$
, then
$\unicode[STIX]{x1D719}$
, then
![]() $T_{{\mathcal{E}}}^{\operatorname{nr}}(M,\unicode[STIX]{x1D719})$
is equal to
$T_{{\mathcal{E}}}^{\operatorname{nr}}(M,\unicode[STIX]{x1D719})$
is equal to
![]() $\{x\in M_{{\mathcal{E}}}^{\operatorname{nr}}\mid \unicode[STIX]{x1D713}(x)=x\}$
, and [Reference FontaineFo1, A 1.2.6] gives the first part of the lemma.
$\{x\in M_{{\mathcal{E}}}^{\operatorname{nr}}\mid \unicode[STIX]{x1D713}(x)=x\}$
, and [Reference FontaineFo1, A 1.2.6] gives the first part of the lemma.
It remains to show that (8.2) is bijective. Assume first that
![]() $(M,\unicode[STIX]{x1D719})$
is a Breuil window, let
$(M,\unicode[STIX]{x1D719})$
is a Breuil window, let
![]() $M^{\ast }=\operatorname{Hom}_{\mathfrak{S}}(M,\mathfrak{S})$
, and let
$M^{\ast }=\operatorname{Hom}_{\mathfrak{S}}(M,\mathfrak{S})$
, and let
![]() $\unicode[STIX]{x1D713}:M^{\ast }\rightarrow M^{\ast }$
be the
$\unicode[STIX]{x1D713}:M^{\ast }\rightarrow M^{\ast }$
be the
![]() $\unicode[STIX]{x1D70E}$
-linear map whose linearization is the dual of
$\unicode[STIX]{x1D70E}$
-linear map whose linearization is the dual of
![]() $\unicode[STIX]{x1D719}$
. Then
$\unicode[STIX]{x1D719}$
. Then
![]() $(M^{\ast },\unicode[STIX]{x1D713})$
is a Kisin module as considered in [Reference KisinKi1, (2.1.3)], and
$(M^{\ast },\unicode[STIX]{x1D713})$
is a Kisin module as considered in [Reference KisinKi1, (2.1.3)], and
![]() $T^{\operatorname{nr}}(M,\unicode[STIX]{x1D719})$
can be identified with the module of
$T^{\operatorname{nr}}(M,\unicode[STIX]{x1D719})$
can be identified with the module of
![]() $\mathfrak{S}$
-linear maps
$\mathfrak{S}$
-linear maps
![]() $\unicode[STIX]{x1D706}:M^{\ast }\rightarrow \mathfrak{S}^{\operatorname{nr}}$
with
$\unicode[STIX]{x1D706}:M^{\ast }\rightarrow \mathfrak{S}^{\operatorname{nr}}$
with
![]() $\unicode[STIX]{x1D70E}\unicode[STIX]{x1D706}=\unicode[STIX]{x1D706}\unicode[STIX]{x1D713}$
, and similarly for
$\unicode[STIX]{x1D70E}\unicode[STIX]{x1D706}=\unicode[STIX]{x1D706}\unicode[STIX]{x1D713}$
, and similarly for
![]() $T_{{\mathcal{E}}}^{\operatorname{nr}}(M,\unicode[STIX]{x1D719})$
. Thus (8.2) is bijective by [Reference KisinKi1, Corollary 2.1.4], which builds on [Reference FontaineFo1, B 1.8.4].
$T_{{\mathcal{E}}}^{\operatorname{nr}}(M,\unicode[STIX]{x1D719})$
. Thus (8.2) is bijective by [Reference KisinKi1, Corollary 2.1.4], which builds on [Reference FontaineFo1, B 1.8.4].
Assume now that
![]() $(M,\unicode[STIX]{x1D719})$
is a Breuil module. Using that
$(M,\unicode[STIX]{x1D719})$
is a Breuil module. Using that
![]() $M$
is annihilated by a power of
$M$
is annihilated by a power of
![]() $p$
and of projective dimension
$p$
and of projective dimension
![]() ${\leqslant}1$
and that
${\leqslant}1$
and that
![]() $C={\mathcal{O}}_{\widehat{{\mathcal{E}}^{\operatorname{nr}}}}/\mathfrak{S}^{\operatorname{nr}}$
has no
$C={\mathcal{O}}_{\widehat{{\mathcal{E}}^{\operatorname{nr}}}}/\mathfrak{S}^{\operatorname{nr}}$
has no
![]() $p$
-torsion, we see that
$p$
-torsion, we see that
![]() $\operatorname{Tor}_{1}^{\mathfrak{S}}(C,M)$
is zero. It follows that
$\operatorname{Tor}_{1}^{\mathfrak{S}}(C,M)$
is zero. It follows that
![]() $M^{\operatorname{nr}}\rightarrow M_{{\mathcal{E}}}^{\operatorname{nr}}$
is injective, and thus (8.2) is injective. One can find a Breuil window
$M^{\operatorname{nr}}\rightarrow M_{{\mathcal{E}}}^{\operatorname{nr}}$
is injective, and thus (8.2) is injective. One can find a Breuil window
![]() $(M^{\prime },\unicode[STIX]{x1D719}^{\prime })$
and a surjective map
$(M^{\prime },\unicode[STIX]{x1D719}^{\prime })$
and a surjective map
![]() $(M^{\prime },\unicode[STIX]{x1D719}^{\prime })\rightarrow (M,\unicode[STIX]{x1D719})$
; see (b) in the proof of [Reference LauLa2, Theorem 8.5]. Then
$(M^{\prime },\unicode[STIX]{x1D719}^{\prime })\rightarrow (M,\unicode[STIX]{x1D719})$
; see (b) in the proof of [Reference LauLa2, Theorem 8.5]. Then
![]() $T^{\operatorname{nr}}(M^{\prime },\unicode[STIX]{x1D719}^{\prime })\cong T_{{\mathcal{E}}}^{\operatorname{nr}}(M^{\prime },\unicode[STIX]{x1D719}^{\prime })\rightarrow T_{{\mathcal{E}}}^{\operatorname{nr}}(M,\unicode[STIX]{x1D719})$
is surjective, and thus (8.2) is surjective.◻
$T^{\operatorname{nr}}(M^{\prime },\unicode[STIX]{x1D719}^{\prime })\cong T_{{\mathcal{E}}}^{\operatorname{nr}}(M^{\prime },\unicode[STIX]{x1D719}^{\prime })\rightarrow T_{{\mathcal{E}}}^{\operatorname{nr}}(M,\unicode[STIX]{x1D719})$
is surjective, and thus (8.2) is surjective.◻
8.2 The choice of
 $K_{\infty }$
$K_{\infty }$
Let
![]() $\bar{\mathfrak{m}}^{\wedge }$
be the maximal ideal of
$\bar{\mathfrak{m}}^{\wedge }$
be the maximal ideal of
![]() $\bar{R}^{\wedge }$
. The power series
$\bar{R}^{\wedge }$
. The power series
![]() $\unicode[STIX]{x1D70E}(t)$
defines a map
$\unicode[STIX]{x1D70E}(t)$
defines a map
![]() $\unicode[STIX]{x1D70E}(t):\bar{\mathfrak{m}}^{\wedge }\rightarrow \bar{\mathfrak{m}}^{\wedge }$
. This map is surjective, and the inverse images of algebraic elements are algebraic by the Weierstrass preparation theorem. Choose a system of elements
$\unicode[STIX]{x1D70E}(t):\bar{\mathfrak{m}}^{\wedge }\rightarrow \bar{\mathfrak{m}}^{\wedge }$
. This map is surjective, and the inverse images of algebraic elements are algebraic by the Weierstrass preparation theorem. Choose a system of elements
![]() $(\unicode[STIX]{x1D70B}^{(n)})_{n\geqslant 0}$
of
$(\unicode[STIX]{x1D70B}^{(n)})_{n\geqslant 0}$
of
![]() $\bar{K}$
with
$\bar{K}$
with
![]() $\unicode[STIX]{x1D70B}^{(0)}=\unicode[STIX]{x1D70B}$
and
$\unicode[STIX]{x1D70B}^{(0)}=\unicode[STIX]{x1D70B}$
and
![]() $\unicode[STIX]{x1D70E}(t)(\unicode[STIX]{x1D70B}^{(n+1)})=\unicode[STIX]{x1D70B}^{(n)}$
, and let
$\unicode[STIX]{x1D70E}(t)(\unicode[STIX]{x1D70B}^{(n+1)})=\unicode[STIX]{x1D70B}^{(n)}$
, and let
![]() $K_{\infty }$
be the extension of
$K_{\infty }$
be the extension of
![]() $K$
generated by all
$K$
generated by all
![]() $\unicode[STIX]{x1D70B}^{(n)}$
. The system
$\unicode[STIX]{x1D70B}^{(n)}$
. The system
![]() $(\unicode[STIX]{x1D70B}^{(n)})$
corresponds to an element
$(\unicode[STIX]{x1D70B}^{(n)})$
corresponds to an element
![]() $\text{}\underline{\unicode[STIX]{x1D70B}}\in {\mathcal{R}}=\varprojlim \bar{R}/p\bar{R}$
, the limit taken with respect to Frobenius.
$\text{}\underline{\unicode[STIX]{x1D70B}}\in {\mathcal{R}}=\varprojlim \bar{R}/p\bar{R}$
, the limit taken with respect to Frobenius.
We embed
![]() ${\mathcal{O}}_{\mathbb{E}}=k[[t]]$
into
${\mathcal{O}}_{\mathbb{E}}=k[[t]]$
into
![]() ${\mathcal{R}}$
by
${\mathcal{R}}$
by
![]() $t\mapsto \text{}\underline{\unicode[STIX]{x1D70B}}$
, and identify
$t\mapsto \text{}\underline{\unicode[STIX]{x1D70B}}$
, and identify
![]() $\mathbb{E}^{\operatorname{sep}}$
and
$\mathbb{E}^{\operatorname{sep}}$
and
![]() $\bar{\mathbb{E}}$
with subfields of
$\bar{\mathbb{E}}$
with subfields of
![]() $\operatorname{Frac}{\mathcal{R}}$
; thus
$\operatorname{Frac}{\mathcal{R}}$
; thus
![]() $W(\bar{\mathbb{E}})\subset W(\operatorname{Frac}{\mathcal{R}})$
. Then
$W(\bar{\mathbb{E}})\subset W(\operatorname{Frac}{\mathcal{R}})$
. Then
![]() $\mathfrak{S}^{\operatorname{nr}}={\mathcal{O}}_{\widehat{{\mathcal{E}}^{\operatorname{nr}}}}\cap W({\mathcal{R}})$
, and the unique ring homomorphism
$\mathfrak{S}^{\operatorname{nr}}={\mathcal{O}}_{\widehat{{\mathcal{E}}^{\operatorname{nr}}}}\cap W({\mathcal{R}})$
, and the unique ring homomorphism
![]() $\unicode[STIX]{x1D703}:W({\mathcal{R}})\rightarrow \bar{R}^{\wedge }$
which lifts the projection
$\unicode[STIX]{x1D703}:W({\mathcal{R}})\rightarrow \bar{R}^{\wedge }$
which lifts the projection
![]() $W({\mathcal{R}})\rightarrow \bar{R}/p\bar{R}$
induces a homomorphism
$W({\mathcal{R}})\rightarrow \bar{R}/p\bar{R}$
induces a homomorphism
Let us verify that its restriction to
![]() $\mathfrak{S}$
is the given projection
$\mathfrak{S}$
is the given projection
![]() $\mathfrak{S}\rightarrow R$
.
$\mathfrak{S}\rightarrow R$
.
Lemma 8.2. We have
![]() $pr^{\operatorname{nr}}(t)=\unicode[STIX]{x1D70B}$
.
$pr^{\operatorname{nr}}(t)=\unicode[STIX]{x1D70B}$
.
Proof. The lemma is easy if
![]() $\unicode[STIX]{x1D70E}(t)=t^{p}$
since then
$\unicode[STIX]{x1D70E}(t)=t^{p}$
since then
![]() $\unicode[STIX]{x1D6E5}(t)=[t]$
in
$\unicode[STIX]{x1D6E5}(t)=[t]$
in
![]() $W(\mathfrak{S})$
, which maps to
$W(\mathfrak{S})$
, which maps to
![]() $[\text{}\underline{\unicode[STIX]{x1D70B}}]$
in
$[\text{}\underline{\unicode[STIX]{x1D70B}}]$
in
![]() $W({\mathcal{R}})$
, and
$W({\mathcal{R}})$
, and
![]() $\unicode[STIX]{x1D703}([\text{}\underline{\unicode[STIX]{x1D70B}}])=\unicode[STIX]{x1D70B}$
in this case. In general let
$\unicode[STIX]{x1D703}([\text{}\underline{\unicode[STIX]{x1D70B}}])=\unicode[STIX]{x1D70B}$
in this case. In general let
![]() $\unicode[STIX]{x1D6E5}(t)=(g_{0},g_{1},\ldots )$
with
$\unicode[STIX]{x1D6E5}(t)=(g_{0},g_{1},\ldots )$
with
![]() $g_{i}\in \mathfrak{S}$
; these power series are determined by the relations
$g_{i}\in \mathfrak{S}$
; these power series are determined by the relations
for
![]() $n\geqslant 0$
. Let
$n\geqslant 0$
. Let
![]() $x=(x_{0},x_{1},\ldots )\in W({\mathcal{R}})$
be the image of
$x=(x_{0},x_{1},\ldots )\in W({\mathcal{R}})$
be the image of
![]() $t$
, thus
$t$
, thus
![]() $x_{i}=g_{i}(\text{}\underline{\unicode[STIX]{x1D70B}})$
. Write
$x_{i}=g_{i}(\text{}\underline{\unicode[STIX]{x1D70B}})$
. Write
![]() $x_{i}=(x_{i,0},x_{i,1},\ldots )$
with
$x_{i}=(x_{i,0},x_{i,1},\ldots )$
with
![]() $x_{i,n}=g_{i}(\text{}\underline{\unicode[STIX]{x1D70B}})_{n}\in \bar{R}/p\bar{R}$
. If
$x_{i,n}=g_{i}(\text{}\underline{\unicode[STIX]{x1D70B}})_{n}\in \bar{R}/p\bar{R}$
. If
![]() $\tilde{x}_{i,n}\in \bar{R}^{\wedge }$
lifts
$\tilde{x}_{i,n}\in \bar{R}^{\wedge }$
lifts
![]() $x_{i,n}$
we have
$x_{i,n}$
we have
If we choose
![]() $\tilde{x}_{i,n}=g_{i}(\unicode[STIX]{x1D70B}^{(n)})$
, the sum in the limit becomes
$\tilde{x}_{i,n}=g_{i}(\unicode[STIX]{x1D70B}^{(n)})$
, the sum in the limit becomes
![]() $\unicode[STIX]{x1D70E}^{n}(t)(\unicode[STIX]{x1D70B}^{(n)})=\unicode[STIX]{x1D70B}$
, and the lemma is proved.◻
$\unicode[STIX]{x1D70E}^{n}(t)(\unicode[STIX]{x1D70B}^{(n)})=\unicode[STIX]{x1D70B}$
, and the lemma is proved.◻
The natural action of
![]() ${\mathcal{G}}_{K_{\infty }}=\operatorname{Gal}(\bar{K}/K_{\infty })$
on
${\mathcal{G}}_{K_{\infty }}=\operatorname{Gal}(\bar{K}/K_{\infty })$
on
![]() $W(\operatorname{Frac}{\mathcal{R}})$
is trivial on
$W(\operatorname{Frac}{\mathcal{R}})$
is trivial on
![]() ${\mathcal{O}}_{{\mathcal{E}}}$
, and therefore it stabilizes
${\mathcal{O}}_{{\mathcal{E}}}$
, and therefore it stabilizes
![]() ${\mathcal{O}}_{\hat{{\mathcal{E}}}^{\operatorname{nr}}}$
and
${\mathcal{O}}_{\hat{{\mathcal{E}}}^{\operatorname{nr}}}$
and
![]() $\mathfrak{S}^{\operatorname{nr}}$
with trivial action on
$\mathfrak{S}^{\operatorname{nr}}$
with trivial action on
![]() $\mathfrak{S}$
. Thus
$\mathfrak{S}$
. Thus
![]() ${\mathcal{G}}_{K_{\infty }}$
acts on
${\mathcal{G}}_{K_{\infty }}$
acts on
![]() $T^{\operatorname{nr}}(M,\unicode[STIX]{x1D719})$
for each Breuil window or Breuil module
$T^{\operatorname{nr}}(M,\unicode[STIX]{x1D719})$
for each Breuil window or Breuil module
![]() $(M,\unicode[STIX]{x1D719})$
.
$(M,\unicode[STIX]{x1D719})$
.
8.3 From
 $\mathfrak{S}^{\operatorname{nr}}$
to Zink rings
$\mathfrak{S}^{\operatorname{nr}}$
to Zink rings
The composition of the inclusion
![]() $\mathfrak{S}^{\operatorname{nr}}\rightarrow W({\mathcal{R}})$
chosen above with the homomorphism
$\mathfrak{S}^{\operatorname{nr}}\rightarrow W({\mathcal{R}})$
chosen above with the homomorphism
![]() $\unicode[STIX]{x1D718}_{\inf }:W({\mathcal{R}})\rightarrow \hat{\mathbb{W}}(\tilde{R})$
from Lemma 6.1 is a ring homomorphism
$\unicode[STIX]{x1D718}_{\inf }:W({\mathcal{R}})\rightarrow \hat{\mathbb{W}}(\tilde{R})$
from Lemma 6.1 is a ring homomorphism
that commutes with Frobenius and with the projections to
![]() $\bar{R}^{\wedge }$
.
$\bar{R}^{\wedge }$
.
Lemma 8.3. If the image of
![]() $\unicode[STIX]{x1D718}:\mathfrak{S}\rightarrow W(R)$
lies in
$\unicode[STIX]{x1D718}:\mathfrak{S}\rightarrow W(R)$
lies in
![]() $\mathbb{W}(R)$
, then the following diagram of rings commutes, where the vertical maps are the obvious inclusions.
$\mathbb{W}(R)$
, then the following diagram of rings commutes, where the vertical maps are the obvious inclusions.

Proof. The assumption
![]() $\unicode[STIX]{x1D718}(\mathfrak{S})\subset \mathbb{W}(R)$
is equivalent to
$\unicode[STIX]{x1D718}(\mathfrak{S})\subset \mathbb{W}(R)$
is equivalent to
![]() $\unicode[STIX]{x1D6E5}(\mathfrak{S})\subset \mathbb{W}(\mathfrak{S})$
; see [Reference LauLa3, Proposition 6.2]. As in the proof of Lemma 8.2 we write
$\unicode[STIX]{x1D6E5}(\mathfrak{S})\subset \mathbb{W}(\mathfrak{S})$
; see [Reference LauLa3, Proposition 6.2]. As in the proof of Lemma 8.2 we write
![]() $\unicode[STIX]{x1D6E5}(t)=(g_{0},g_{1},\ldots )$
with
$\unicode[STIX]{x1D6E5}(t)=(g_{0},g_{1},\ldots )$
with
![]() $g_{i}\in \mathfrak{S}$
. Note that
$g_{i}\in \mathfrak{S}$
. Note that
![]() $g_{0}=t$
. We have to show that
$g_{0}=t$
. We have to show that
in
![]() $\hat{\mathbb{W}}(\tilde{R})$
. Again, if
$\hat{\mathbb{W}}(\tilde{R})$
. Again, if
![]() $y_{i,n}\in \hat{\mathbb{W}}(\tilde{R})$
is a lift of
$y_{i,n}\in \hat{\mathbb{W}}(\tilde{R})$
is a lift of
![]() $x_{i,n}=g_{i}(\text{}\underline{\unicode[STIX]{x1D70B}})_{n}\in \bar{R}/p\bar{R}$
, the left hand side of this equation is equal to
$x_{i,n}=g_{i}(\text{}\underline{\unicode[STIX]{x1D70B}})_{n}\in \bar{R}/p\bar{R}$
, the left hand side of this equation is equal to
We will choose
![]() $y_{i,n}\in \mathbb{W}(\tilde{R})$
(no
$y_{i,n}\in \mathbb{W}(\tilde{R})$
(no
![]() $p$
-adic completion) such that the sum in the limit is equal to
$p$
-adic completion) such that the sum in the limit is equal to
![]() $(g_{0}(\unicode[STIX]{x1D70B}),g_{1}(\unicode[STIX]{x1D70B}),\ldots )$
in
$(g_{0}(\unicode[STIX]{x1D70B}),g_{1}(\unicode[STIX]{x1D70B}),\ldots )$
in
![]() $\mathbb{W}(\tilde{R})$
; this will prove the lemma. In the special case
$\mathbb{W}(\tilde{R})$
; this will prove the lemma. In the special case
![]() $\unicode[STIX]{x1D70E}(t)=t^{p}$
we have
$\unicode[STIX]{x1D70E}(t)=t^{p}$
we have
![]() $g_{i}=0$
for
$g_{i}=0$
for
![]() $i\geqslant 1$
, and we can take
$i\geqslant 1$
, and we can take
![]() $y_{0,n}=[\unicode[STIX]{x1D70B}^{(n)}]$
and
$y_{0,n}=[\unicode[STIX]{x1D70B}^{(n)}]$
and
![]() $y_{i,n}=0$
for
$y_{i,n}=0$
for
![]() $i\geqslant 1$
; then the calculation is trivial. In general, let
$i\geqslant 1$
; then the calculation is trivial. In general, let
![]() $\unicode[STIX]{x1D6E5}(g_{i})=(h_{i,0},h_{i,1},\ldots )$
in
$\unicode[STIX]{x1D6E5}(g_{i})=(h_{i,0},h_{i,1},\ldots )$
in
![]() $\mathbb{W}(\mathfrak{S})$
, so the power series
$\mathbb{W}(\mathfrak{S})$
, so the power series
![]() $h_{i,j}$
are determined by the equations
$h_{i,j}$
are determined by the equations
for
![]() $m\geqslant 0$
, and put
$m\geqslant 0$
, and put
![]() $y_{i,n}=(h_{i,0}(\unicode[STIX]{x1D70B}^{(n)}),h_{i,1}(\unicode[STIX]{x1D70B}^{(n)}),\ldots )\in \mathbb{W}(\tilde{R})$
. Since the Witt polynomials
$y_{i,n}=(h_{i,0}(\unicode[STIX]{x1D70B}^{(n)}),h_{i,1}(\unicode[STIX]{x1D70B}^{(n)}),\ldots )\in \mathbb{W}(\tilde{R})$
. Since the Witt polynomials
![]() $w_{m}(X_{0},\ldots ,X_{m})=X_{0}^{p^{m}}+\cdots +p^{m}X_{m}$
for
$w_{m}(X_{0},\ldots ,X_{m})=X_{0}^{p^{m}}+\cdots +p^{m}X_{m}$
for
![]() $m\geqslant 0$
define an injective map
$m\geqslant 0$
define an injective map
![]() $\mathbb{W}(\tilde{R})\subset W(\tilde{R})\rightarrow \tilde{R}^{\infty }$
, we have to show that for
$\mathbb{W}(\tilde{R})\subset W(\tilde{R})\rightarrow \tilde{R}^{\infty }$
, we have to show that for
![]() $n,m\geqslant 0$
the following holds.
$n,m\geqslant 0$
the following holds.
The right hand side is equal to
![]() $\unicode[STIX]{x1D70E}^{m}(t)(\unicode[STIX]{x1D70B})$
. Since
$\unicode[STIX]{x1D70E}^{m}(t)(\unicode[STIX]{x1D70B})$
. Since
![]() $w_{m}$
is a ring homomorphism and since
$w_{m}$
is a ring homomorphism and since
![]() $w_{m}(y_{i,n})=g_{i}(\unicode[STIX]{x1D70E}^{m}(t)(\unicode[STIX]{x1D70B}^{(n)}))$
, the left hand side is equal to
$w_{m}(y_{i,n})=g_{i}(\unicode[STIX]{x1D70E}^{m}(t)(\unicode[STIX]{x1D70B}^{(n)}))$
, the left hand side is equal to
![]() $\unicode[STIX]{x1D70E}^{n}(t)(\unicode[STIX]{x1D70E}^{m}(t)(\unicode[STIX]{x1D70B}^{(n)}))=\unicode[STIX]{x1D70E}^{n+m}(t)(\unicode[STIX]{x1D70B}^{(n)})=\unicode[STIX]{x1D70E}^{m}(t)(\unicode[STIX]{x1D70B})$
too.◻
$\unicode[STIX]{x1D70E}^{n}(t)(\unicode[STIX]{x1D70E}^{m}(t)(\unicode[STIX]{x1D70B}^{(n)}))=\unicode[STIX]{x1D70E}^{n+m}(t)(\unicode[STIX]{x1D70B}^{(n)})=\unicode[STIX]{x1D70E}^{m}(t)(\unicode[STIX]{x1D70B})$
too.◻
We define a frame
with
![]() $\unicode[STIX]{x1D70E}_{1}(Ex)=\unicode[STIX]{x1D70E}(x)$
for
$\unicode[STIX]{x1D70E}_{1}(Ex)=\unicode[STIX]{x1D70E}(x)$
for
![]() $x\in \mathfrak{S}^{\operatorname{nr}}$
.
$x\in \mathfrak{S}^{\operatorname{nr}}$
.
Lemma 8.4. The element
![]() $u^{\prime }=f_{1}(\unicode[STIX]{x1D718}^{\operatorname{nr}}(E))\in \hat{\mathbb{W}}(\tilde{R})$
is a unit, and the ring homomorphism
$u^{\prime }=f_{1}(\unicode[STIX]{x1D718}^{\operatorname{nr}}(E))\in \hat{\mathbb{W}}(\tilde{R})$
is a unit, and the ring homomorphism
![]() $\unicode[STIX]{x1D718}^{\operatorname{nr}}:\mathfrak{S}^{\operatorname{nr}}\rightarrow \hat{\mathbb{W}}(\tilde{R})$
is a
$\unicode[STIX]{x1D718}^{\operatorname{nr}}:\mathfrak{S}^{\operatorname{nr}}\rightarrow \hat{\mathbb{W}}(\tilde{R})$
is a
![]() $u^{\prime }$
-homomorphism of frames
$u^{\prime }$
-homomorphism of frames
![]() $\unicode[STIX]{x1D718}^{\operatorname{nr}}:\mathscr{B}^{\operatorname{nr}}\rightarrow \hat{\mathscr{D}}_{\tilde{R}}$
.
$\unicode[STIX]{x1D718}^{\operatorname{nr}}:\mathscr{B}^{\operatorname{nr}}\rightarrow \hat{\mathscr{D}}_{\tilde{R}}$
.
Proof. Clearly
![]() $\unicode[STIX]{x1D718}^{\operatorname{nr}}$
commutes with the projections to
$\unicode[STIX]{x1D718}^{\operatorname{nr}}$
commutes with the projections to
![]() $\bar{R}^{\wedge }$
and with the Frobenius. Lemma 8.2 implies that
$\bar{R}^{\wedge }$
and with the Frobenius. Lemma 8.2 implies that
![]() $pr^{\operatorname{nr}}(E)=0$
, thus
$pr^{\operatorname{nr}}(E)=0$
, thus
![]() $\unicode[STIX]{x1D718}^{\operatorname{nr}}(E)\in \hat{\mathbb{I}}_{\tilde{R}}$
. For
$\unicode[STIX]{x1D718}^{\operatorname{nr}}(E)\in \hat{\mathbb{I}}_{\tilde{R}}$
. For
![]() $x\in \mathfrak{S}^{\operatorname{nr}}$
we compute
$x\in \mathfrak{S}^{\operatorname{nr}}$
we compute
![]() $f_{1}(\unicode[STIX]{x1D718}^{\operatorname{nr}}(Ex))=f_{1}(\unicode[STIX]{x1D718}^{\operatorname{nr}}(E))\cdot f(\unicode[STIX]{x1D718}^{\operatorname{nr}}(x))=u^{\prime }\cdot \unicode[STIX]{x1D718}^{\operatorname{nr}}(\unicode[STIX]{x1D70E}_{1}(Ex))$
as required. It remains to show that
$f_{1}(\unicode[STIX]{x1D718}^{\operatorname{nr}}(Ex))=f_{1}(\unicode[STIX]{x1D718}^{\operatorname{nr}}(E))\cdot f(\unicode[STIX]{x1D718}^{\operatorname{nr}}(x))=u^{\prime }\cdot \unicode[STIX]{x1D718}^{\operatorname{nr}}(\unicode[STIX]{x1D70E}_{1}(Ex))$
as required. It remains to show that
![]() $u^{\prime }$
is a unit. The projection
$u^{\prime }$
is a unit. The projection
![]() $\tilde{R}\rightarrow \bar{k}$
induces a local homomorphism of local rings
$\tilde{R}\rightarrow \bar{k}$
induces a local homomorphism of local rings
![]() $\hat{\mathbb{W}}(\tilde{R})\rightarrow W(\bar{k})$
that commutes with
$\hat{\mathbb{W}}(\tilde{R})\rightarrow W(\bar{k})$
that commutes with
![]() $f$
and
$f$
and
![]() $f_{1}$
. The composition
$f_{1}$
. The composition
![]() $\mathfrak{S}\rightarrow \mathfrak{S}^{\operatorname{nr}}\rightarrow \hat{\mathbb{W}}(\tilde{R})\rightarrow W(\bar{k})$
commutes with Frobenius and is thus equal to the homomorphism
$\mathfrak{S}\rightarrow \mathfrak{S}^{\operatorname{nr}}\rightarrow \hat{\mathbb{W}}(\tilde{R})\rightarrow W(\bar{k})$
commutes with Frobenius and is thus equal to the homomorphism
![]() $t\mapsto 0$
. Thus
$t\mapsto 0$
. Thus
![]() $E$
maps to
$E$
maps to
![]() $p$
in
$p$
in
![]() $W(\bar{k})$
, so
$W(\bar{k})$
, so
![]() $u^{\prime }$
maps to
$u^{\prime }$
maps to
![]() $f_{1}(p)=v^{-1}(p)=1$
in
$f_{1}(p)=v^{-1}(p)=1$
in
![]() $W(\bar{k})$
, and it follows that
$W(\bar{k})$
, and it follows that
![]() $u^{\prime }$
is a unit.◻
$u^{\prime }$
is a unit.◻
From now on we assume that the image of
![]() $\unicode[STIX]{x1D718}$
lies in
$\unicode[STIX]{x1D718}$
lies in
![]() $\mathbb{W}(R)$
, so that Lemma 8.3 applies. Then
$\mathbb{W}(R)$
, so that Lemma 8.3 applies. Then
![]() $u^{\prime }$
is the image of
$u^{\prime }$
is the image of
![]() $u\in \mathbb{W}(R)$
, and we get a commutative square of frames where the horizontal arrows are
$u\in \mathbb{W}(R)$
, and we get a commutative square of frames where the horizontal arrows are
![]() $u$
-homomorphisms and the vertical arrows are strict:
$u$
-homomorphisms and the vertical arrows are strict:

Here
![]() ${\mathcal{G}}_{K}$
acts on
${\mathcal{G}}_{K}$
acts on
![]() $\hat{\mathscr{D}}_{\tilde{R}}$
and
$\hat{\mathscr{D}}_{\tilde{R}}$
and
![]() ${\mathcal{G}}_{K_{\infty }}$
acts on
${\mathcal{G}}_{K_{\infty }}$
acts on
![]() $\mathscr{B}^{\operatorname{nr}}$
, and
$\mathscr{B}^{\operatorname{nr}}$
, and
![]() $\unicode[STIX]{x1D718}^{\operatorname{nr}}$
is
$\unicode[STIX]{x1D718}^{\operatorname{nr}}$
is
![]() ${\mathcal{G}}_{K_{\infty }}$
-equivariant.
${\mathcal{G}}_{K_{\infty }}$
-equivariant.
8.4 Identification of modules of invariants
Now we can state the main result of this section. Let
![]() $(M,\unicode[STIX]{x1D719})$
be a Breuil window relative to
$(M,\unicode[STIX]{x1D719})$
be a Breuil window relative to
![]() $\mathfrak{S}\rightarrow R$
with associated
$\mathfrak{S}\rightarrow R$
with associated
![]() $\mathscr{B}$
-window
$\mathscr{B}$
-window
![]() $\mathscr{P}$
, and let
$\mathscr{P}$
, and let
![]() $\mathscr{P}^{\operatorname{nr}}$
be the base change of
$\mathscr{P}^{\operatorname{nr}}$
be the base change of
![]() $\mathscr{P}$
to
$\mathscr{P}$
to
![]() $\mathscr{B}^{\operatorname{nr}}$
. By definition we have
$\mathscr{B}^{\operatorname{nr}}$
. By definition we have
![]() $T^{\operatorname{nr}}(M,\unicode[STIX]{x1D719})=T(\mathscr{P}^{\operatorname{nr}})$
as
$T^{\operatorname{nr}}(M,\unicode[STIX]{x1D719})=T(\mathscr{P}^{\operatorname{nr}})$
as
![]() ${\mathcal{G}}_{K_{\infty }}$
-modules. Let
${\mathcal{G}}_{K_{\infty }}$
-modules. Let
![]() $\mathscr{P}_{\mathscr{D}}$
be the base change of
$\mathscr{P}_{\mathscr{D}}$
be the base change of
![]() $\mathscr{P}$
to
$\mathscr{P}$
to
![]() $\mathscr{D}_{R}$
and let
$\mathscr{D}_{R}$
and let
![]() $\hat{\mathscr{P}}_{\!\tilde{R}}$
be the common base change of
$\hat{\mathscr{P}}_{\!\tilde{R}}$
be the common base change of
![]() $\mathscr{P}^{\operatorname{nr}}$
and
$\mathscr{P}^{\operatorname{nr}}$
and
![]() $\mathscr{P}_{\mathscr{D}}$
to
$\mathscr{P}_{\mathscr{D}}$
to
![]() $\hat{\mathscr{D}}_{\tilde{R}}$
. As in (3.1), multiplication by
$\hat{\mathscr{D}}_{\tilde{R}}$
. As in (3.1), multiplication by
![]() $c$
induces a
$c$
induces a
![]() ${\mathcal{G}}_{K_{\infty }}$
-invariant homomorphism
${\mathcal{G}}_{K_{\infty }}$
-invariant homomorphism
We recall that the
![]() ${\mathcal{G}}_{K}$
-module
${\mathcal{G}}_{K}$
-module
![]() $T(\hat{\mathscr{P}}_{\!\tilde{R}})$
is canonically isomorphic to the Tate module of the
$T(\hat{\mathscr{P}}_{\!\tilde{R}})$
is canonically isomorphic to the Tate module of the
![]() $p$
-divisible group associated to
$p$
-divisible group associated to
![]() $(M,\unicode[STIX]{x1D719})$
; see Proposition 4.1.
$(M,\unicode[STIX]{x1D719})$
; see Proposition 4.1.
Proposition 8.5. The homomorphism
![]() $\unicode[STIX]{x1D70F}(\mathscr{P}^{\operatorname{nr}})$
is bijective.
$\unicode[STIX]{x1D70F}(\mathscr{P}^{\operatorname{nr}})$
is bijective.
Proof. Let
![]() $h$
be the
$h$
be the
![]() $\mathfrak{S}$
-rank of
$\mathfrak{S}$
-rank of
![]() $M$
. The source and target of
$M$
. The source and target of
![]() $\unicode[STIX]{x1D70F}(\mathscr{P}^{\operatorname{nr}})$
are free
$\unicode[STIX]{x1D70F}(\mathscr{P}^{\operatorname{nr}})$
are free
![]() $\mathbb{Z}_{p}$
-modules of rank
$\mathbb{Z}_{p}$
-modules of rank
![]() $h$
which are exact functors of
$h$
which are exact functors of
![]() $\mathscr{P}$
. Indeed, for
$\mathscr{P}$
. Indeed, for
![]() $T(\mathscr{P}^{\operatorname{nr}})=T^{\operatorname{nr}}(M,\unicode[STIX]{x1D719})$
this follows from Lemma 8.1, and it holds for
$T(\mathscr{P}^{\operatorname{nr}})=T^{\operatorname{nr}}(M,\unicode[STIX]{x1D719})$
this follows from Lemma 8.1, and it holds for
![]() $T(\hat{\mathscr{P}}_{\!\tilde{R}})$
by Proposition 4.1, using that the height of a
$T(\hat{\mathscr{P}}_{\!\tilde{R}})$
by Proposition 4.1, using that the height of a
![]() $p$
-divisible group is equal to the rank of its Dieudonné display; this can be verified over perfect fields, and then the Dieudonné display is the classical Dieudonné module.
$p$
-divisible group is equal to the rank of its Dieudonné display; this can be verified over perfect fields, and then the Dieudonné display is the classical Dieudonné module.
Consider first the case where the
![]() $p$
-divisible group associated to
$p$
-divisible group associated to
![]() $\mathscr{P}$
is étale, which means that
$\mathscr{P}$
is étale, which means that
![]() $\mathscr{P}=(P,Q,F,F_{1})$
has
$\mathscr{P}=(P,Q,F,F_{1})$
has
![]() $P=Q$
, and
$P=Q$
, and
![]() $F_{1}:Q\rightarrow P$
is a
$F_{1}:Q\rightarrow P$
is a
![]() $\unicode[STIX]{x1D70E}$
-linear isomorphism. Then
$\unicode[STIX]{x1D70E}$
-linear isomorphism. Then
![]() $(P,F_{1})$
is an étale
$(P,F_{1})$
is an étale
![]() $\unicode[STIX]{x1D70E}$
-module over
$\unicode[STIX]{x1D70E}$
-module over
![]() $\mathfrak{S}$
. Since
$\mathfrak{S}$
. Since
![]() $\mathfrak{S}^{\operatorname{nr}}$
is
$\mathfrak{S}^{\operatorname{nr}}$
is
![]() $p$
-adically complete with
$p$
-adically complete with
![]() $\mathfrak{S}^{\operatorname{nr}}/p={\mathcal{O}}_{\mathbb{E}^{\operatorname{sep}}}$
, a
$\mathfrak{S}^{\operatorname{nr}}/p={\mathcal{O}}_{\mathbb{E}^{\operatorname{sep}}}$
, a
![]() $\mathbb{Z}_{p}$
-basis of
$\mathbb{Z}_{p}$
-basis of
![]() $T(\mathscr{P}^{\operatorname{nr}})$
is an
$T(\mathscr{P}^{\operatorname{nr}})$
is an
![]() $\mathfrak{S}^{\operatorname{nr}}$
-basis of
$\mathfrak{S}^{\operatorname{nr}}$
-basis of
![]() $P^{\operatorname{nr}}$
. Using Lemma 4.3 it follows that a
$P^{\operatorname{nr}}$
. Using Lemma 4.3 it follows that a
![]() $\mathbb{Z}_{p}$
-basis of
$\mathbb{Z}_{p}$
-basis of
![]() $T(\hat{\mathscr{P}}_{\!\tilde{R}})$
is a
$T(\hat{\mathscr{P}}_{\!\tilde{R}})$
is a
![]() $\hat{\mathbb{W}}(\tilde{R})$
-basis of
$\hat{\mathbb{W}}(\tilde{R})$
-basis of
![]() $\hat{P}_{\tilde{R}}=\hat{\mathbb{W}}(\tilde{R})\otimes _{\mathfrak{S}^{\operatorname{nr}}}P^{\operatorname{nr}}$
. Thus the homomorphism of
$\hat{P}_{\tilde{R}}=\hat{\mathbb{W}}(\tilde{R})\otimes _{\mathfrak{S}^{\operatorname{nr}}}P^{\operatorname{nr}}$
. Thus the homomorphism of
![]() $\mathbb{Z}_{p}$
-modules
$\mathbb{Z}_{p}$
-modules
![]() $\unicode[STIX]{x1D70F}(\mathscr{P}^{\operatorname{nr}})$
becomes an isomorphism over
$\unicode[STIX]{x1D70F}(\mathscr{P}^{\operatorname{nr}})$
becomes an isomorphism over
![]() $\hat{\mathbb{W}}(\tilde{R})$
. Since
$\hat{\mathbb{W}}(\tilde{R})$
. Since
![]() $\mathbb{Z}_{p}\rightarrow \hat{\mathbb{W}}(\tilde{R})$
is a local homomorphism it follows that
$\mathbb{Z}_{p}\rightarrow \hat{\mathbb{W}}(\tilde{R})$
is a local homomorphism it follows that
![]() $\unicode[STIX]{x1D70F}(\mathscr{P}^{\operatorname{nr}})$
is bijective.
$\unicode[STIX]{x1D70F}(\mathscr{P}^{\operatorname{nr}})$
is bijective.
Consider next the case
![]() $\mathscr{P}=\mathscr{B}$
, which corresponds to the
$\mathscr{P}=\mathscr{B}$
, which corresponds to the
![]() $p$
-divisible group
$p$
-divisible group
![]() $\unicode[STIX]{x1D707}_{p^{\infty }}$
. Assume that the proposition does not hold for
$\unicode[STIX]{x1D707}_{p^{\infty }}$
. Assume that the proposition does not hold for
![]() $\mathscr{B}$
, i.e., that
$\mathscr{B}$
, i.e., that
![]() $\unicode[STIX]{x1D70F}(\mathscr{B}^{\operatorname{nr}})$
is divisible by
$\unicode[STIX]{x1D70F}(\mathscr{B}^{\operatorname{nr}})$
is divisible by
![]() $p$
. For a perfect extension
$p$
. For a perfect extension
![]() $k^{\prime }$
of
$k^{\prime }$
of
![]() $k$
let
$k$
let
![]() $\mathfrak{S}^{\prime }=W(k^{\prime })[[t]]$
and
$\mathfrak{S}^{\prime }=W(k^{\prime })[[t]]$
and
![]() $R^{\prime }=\mathfrak{S}^{\prime }/E\mathfrak{S}^{\prime }$
, and let
$R^{\prime }=\mathfrak{S}^{\prime }/E\mathfrak{S}^{\prime }$
, and let
![]() $\mathscr{B}^{\prime }$
be the corresponding analogue of the frame
$\mathscr{B}^{\prime }$
be the corresponding analogue of the frame
![]() $\mathscr{B}$
; note that the Frobenius lift
$\mathscr{B}$
; note that the Frobenius lift
![]() $\unicode[STIX]{x1D70E}$
of
$\unicode[STIX]{x1D70E}$
of
![]() $\mathfrak{S}$
extends uniquely to
$\mathfrak{S}$
extends uniquely to
![]() $\mathfrak{S}^{\prime }$
. The natural homomorphism
$\mathfrak{S}^{\prime }$
. The natural homomorphism
![]() $T(\mathscr{B}^{\operatorname{nr}})\rightarrow T({\mathscr{B}^{\prime }}^{\operatorname{nr}})$
is bijective because it becomes bijective over
$T(\mathscr{B}^{\operatorname{nr}})\rightarrow T({\mathscr{B}^{\prime }}^{\operatorname{nr}})$
is bijective because it becomes bijective over
![]() ${\mathcal{O}}_{\widehat{{{\mathcal{E}}^{\prime }}^{\operatorname{nr}}}}$
by Lemma 8.1. The natural homomorphism
${\mathcal{O}}_{\widehat{{{\mathcal{E}}^{\prime }}^{\operatorname{nr}}}}$
by Lemma 8.1. The natural homomorphism
![]() $T(\hat{\mathscr{D}}_{\tilde{R}})\rightarrow T(\hat{\mathscr{D}}_{\tilde{R}^{\prime }})$
is bijective since the equivalence between
$T(\hat{\mathscr{D}}_{\tilde{R}})\rightarrow T(\hat{\mathscr{D}}_{\tilde{R}^{\prime }})$
is bijective since the equivalence between
![]() $p$
-divisible groups and Dieudonné displays is compatible with arbitrary base change by [Reference LauLa3, Lemma 9.6]. Hence the homomorphism
$p$
-divisible groups and Dieudonné displays is compatible with arbitrary base change by [Reference LauLa3, Lemma 9.6]. Hence the homomorphism
![]() $\unicode[STIX]{x1D70F}(\mathscr{B}^{\operatorname{nr}})$
can be identified with
$\unicode[STIX]{x1D70F}(\mathscr{B}^{\operatorname{nr}})$
can be identified with
![]() $\unicode[STIX]{x1D70F}({\mathscr{B}^{\prime }}^{\operatorname{nr}})$
, so
$\unicode[STIX]{x1D70F}({\mathscr{B}^{\prime }}^{\operatorname{nr}})$
, so
![]() $k$
can be replaced by
$k$
can be replaced by
![]() $k^{\prime }$
, which allows to assume that
$k^{\prime }$
, which allows to assume that
![]() $k$
is uncountable. Let
$k$
is uncountable. Let
![]() $\mathscr{P}_{0}$
be the étale
$\mathscr{P}_{0}$
be the étale
![]() $\mathscr{B}$
-window that corresponds to
$\mathscr{B}$
-window that corresponds to
![]() $\mathbb{Q}_{p}/\mathbb{Z}_{p}$
. We consider extensions of
$\mathbb{Q}_{p}/\mathbb{Z}_{p}$
. We consider extensions of
![]() $\mathscr{B}$
-windows
$\mathscr{B}$
-windows
![]() $0\rightarrow \mathscr{B}\rightarrow \mathscr{P}_{1}\rightarrow \mathscr{P}_{0}\rightarrow 0$
, which correspond to extensions in
$0\rightarrow \mathscr{B}\rightarrow \mathscr{P}_{1}\rightarrow \mathscr{P}_{0}\rightarrow 0$
, which correspond to extensions in
![]() $\operatorname{Ext}_{R}^{1}(\mathbb{Q}_{p}/\mathbb{Z}_{p},\unicode[STIX]{x1D707}_{p^{\infty }})$
. Since
$\operatorname{Ext}_{R}^{1}(\mathbb{Q}_{p}/\mathbb{Z}_{p},\unicode[STIX]{x1D707}_{p^{\infty }})$
. Since
![]() $\unicode[STIX]{x1D70F}(\mathscr{P}_{0}^{\operatorname{nr}})$
is bijective and
$\unicode[STIX]{x1D70F}(\mathscr{P}_{0}^{\operatorname{nr}})$
is bijective and
![]() $\unicode[STIX]{x1D70F}(\mathscr{B}^{\operatorname{nr}})$
is divisible by
$\unicode[STIX]{x1D70F}(\mathscr{B}^{\operatorname{nr}})$
is divisible by
![]() $p$
, the image of
$p$
, the image of
![]() $\unicode[STIX]{x1D70F}(\mathscr{P}_{1}^{\operatorname{nr}})$
provides a splitting of the reduction modulo
$\unicode[STIX]{x1D70F}(\mathscr{P}_{1}^{\operatorname{nr}})$
provides a splitting of the reduction modulo
![]() $p$
of the exact sequence of
$p$
of the exact sequence of
![]() ${\mathcal{G}}_{K_{\infty }}$
-modules
${\mathcal{G}}_{K_{\infty }}$
-modules
Hence the composite homomorphism
is zero. The first group in (8.3) can be identified with the set of deformations of
![]() $\mathbb{Q}_{p}/\mathbb{Z}_{p}\oplus \unicode[STIX]{x1D707}_{p^{\infty }}$
from
$\mathbb{Q}_{p}/\mathbb{Z}_{p}\oplus \unicode[STIX]{x1D707}_{p^{\infty }}$
from
![]() $k$
to
$k$
to
![]() $R$
. The second group is isomorphic to
$R$
. The second group is isomorphic to
![]() $\operatorname{Ext}_{K}^{1}(\mathbb{Z},\unicode[STIX]{x1D707}_{p})$
, which is isomorphic to the Galois cohomology group
$\operatorname{Ext}_{K}^{1}(\mathbb{Z},\unicode[STIX]{x1D707}_{p})$
, which is isomorphic to the Galois cohomology group
![]() $H^{1}({\mathcal{G}}_{K},\unicode[STIX]{x1D707}_{p})\cong K^{\ast }/(K^{\ast })^{p}$
. As in [Reference LauLa1, Lemma 7.2] it follows that the first arrow in (8.3) can be identified with the natural map
$H^{1}({\mathcal{G}}_{K},\unicode[STIX]{x1D707}_{p})\cong K^{\ast }/(K^{\ast })^{p}$
. As in [Reference LauLa1, Lemma 7.2] it follows that the first arrow in (8.3) can be identified with the natural map
![]() $1+\mathfrak{m}_{R}\rightarrow K^{\ast }/(K^{\ast })^{p}$
, whose image is uncountable since
$1+\mathfrak{m}_{R}\rightarrow K^{\ast }/(K^{\ast })^{p}$
, whose image is uncountable since
![]() $k$
is uncountable. Since for a finite extension
$k$
is uncountable. Since for a finite extension
![]() $K^{\prime }/K$
the homomorphism
$K^{\prime }/K$
the homomorphism
![]() $H^{1}(K,\unicode[STIX]{x1D707}_{p})\rightarrow H^{1}(K^{\prime },\unicode[STIX]{x1D707}_{p})$
has finite kernel by the inflation-restriction exact sequence, the kernel of the second map in (8.3) is countable. Thus the composition (8.3) cannot be zero, and the proposition is proved for
$H^{1}(K,\unicode[STIX]{x1D707}_{p})\rightarrow H^{1}(K^{\prime },\unicode[STIX]{x1D707}_{p})$
has finite kernel by the inflation-restriction exact sequence, the kernel of the second map in (8.3) is countable. Thus the composition (8.3) cannot be zero, and the proposition is proved for
![]() $\mathscr{P}=\mathscr{B}$
.
$\mathscr{P}=\mathscr{B}$
.
Finally let
![]() $\mathscr{P}$
be arbitrary. Duality gives the following commutative diagram; see the end of Section 3.
$\mathscr{P}$
be arbitrary. Duality gives the following commutative diagram; see the end of Section 3.

The upper line of (8.4) is a bilinear form of free
![]() $\mathbb{Z}_{p}$
-modules of rank
$\mathbb{Z}_{p}$
-modules of rank
![]() $h$
, whose scalar extension under
$h$
, whose scalar extension under
![]() $\mathbb{Z}_{p}\rightarrow {\mathcal{O}}_{\widehat{{\mathcal{E}}^{\operatorname{nr}}}}$
is perfect since (8.2) and (8.1) are bijective. Since this is a local homomorphism the upper line of (8.4) is perfect. Proposition 4.1 implies that the lower line of (8.4) is a bilinear form of free
$\mathbb{Z}_{p}\rightarrow {\mathcal{O}}_{\widehat{{\mathcal{E}}^{\operatorname{nr}}}}$
is perfect since (8.2) and (8.1) are bijective. Since this is a local homomorphism the upper line of (8.4) is perfect. Proposition 4.1 implies that the lower line of (8.4) is a bilinear form of free
![]() $\mathbb{Z}_{p}$
-modules of rank
$\mathbb{Z}_{p}$
-modules of rank
![]() $h$
. We have seen that
$h$
. We have seen that
![]() $\unicode[STIX]{x1D70F}(\mathscr{B}^{\operatorname{nr}})$
is bijective. These properties imply that
$\unicode[STIX]{x1D70F}(\mathscr{B}^{\operatorname{nr}})$
is bijective. These properties imply that
![]() $\unicode[STIX]{x1D70F}(\mathscr{P}^{\operatorname{nr}})$
is bijective.◻
$\unicode[STIX]{x1D70F}(\mathscr{P}^{\operatorname{nr}})$
is bijective.◻
For a
![]() $p$
-divisible group or commutative finite flat
$p$
-divisible group or commutative finite flat
![]() $p$
-group scheme
$p$
-group scheme
![]() $G$
over
$G$
over
![]() $R$
let
$R$
let
![]() $(M(G),\unicode[STIX]{x1D719})$
be the associated Breuil window or Breuil module. In the first case let
$(M(G),\unicode[STIX]{x1D719})$
be the associated Breuil window or Breuil module. In the first case let
![]() $T(G)$
be the Tate module of
$T(G)$
be the Tate module of
![]() $G$
, and in the second case let
$G$
, and in the second case let
![]() $T(G)=G(\bar{K})$
.
$T(G)=G(\bar{K})$
.
Corollary 8.6. There is an isomorphism of
![]() ${\mathcal{G}}_{K_{\infty }}$
-modules
${\mathcal{G}}_{K_{\infty }}$
-modules
![]() $T(G)\cong T^{\operatorname{nr}}(M(G),\unicode[STIX]{x1D719})$
.
$T(G)\cong T^{\operatorname{nr}}(M(G),\unicode[STIX]{x1D719})$
.
Proof. For
![]() $p$
-divisible groups this is immediate from Propositions 4.1 and 8.5. The finite case follows from the
$p$
-divisible groups this is immediate from Propositions 4.1 and 8.5. The finite case follows from the
![]() $p$
-divisible case as in the proof of [Reference LauLa3, Corollary 6.8]. More precisely, a finite
$p$
-divisible case as in the proof of [Reference LauLa3, Corollary 6.8]. More precisely, a finite
![]() $G$
can be written as the kernel of an isogeny of
$G$
can be written as the kernel of an isogeny of
![]() $p$
-divisible groups
$p$
-divisible groups
![]() $G_{0}\rightarrow G_{1}$
, which gives exact sequences
$G_{0}\rightarrow G_{1}$
, which gives exact sequences
![]() $0\rightarrow T(G_{0})\rightarrow T(G_{1})\rightarrow T(G)\rightarrow 0$
and
$0\rightarrow T(G_{0})\rightarrow T(G_{1})\rightarrow T(G)\rightarrow 0$
and
![]() $0\rightarrow M(G_{0})\rightarrow M(G_{1})\rightarrow M(G)\rightarrow 0$
, and the latter gives an exact sequence
$0\rightarrow M(G_{0})\rightarrow M(G_{1})\rightarrow M(G)\rightarrow 0$
, and the latter gives an exact sequence
![]() $0\rightarrow T^{\operatorname{nr}}(M(G_{0}))\rightarrow T^{\operatorname{nr}}(M(G_{1}))\rightarrow T^{\operatorname{nr}}(M(G))\rightarrow 0$
. The resulting isomorphism
$0\rightarrow T^{\operatorname{nr}}(M(G_{0}))\rightarrow T^{\operatorname{nr}}(M(G_{1}))\rightarrow T^{\operatorname{nr}}(M(G))\rightarrow 0$
. The resulting isomorphism
![]() $T(G)\cong T^{\operatorname{nr}}(M(G))$
is independent of the resolution
$T(G)\cong T^{\operatorname{nr}}(M(G))$
is independent of the resolution
![]() $G_{0}\rightarrow G_{1}$
of
$G_{0}\rightarrow G_{1}$
of
![]() $G$
.◻
$G$
.◻
Acknowledgments
The author thanks Th. Zink for interesting and helpful discussions, and the anonymous referee for many detailed suggestions to improve the presentation.