Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-10T17:29:26.896Z Has data issue: false hasContentIssue false
  • English
  • Français

DISTRIBUTION OF GALOIS GROUPS OF MAXIMAL UNRAMIFIED 2-EXTENSIONS OVER IMAGINARY QUADRATIC FIELDS

Part of: Algebraic number theory: global fields

Published online by Cambridge University Press:  09 July 2018

SOSUKE SASAKI
SOSUKE SASAKI*
Affiliation:
Department of Pure and Applied Mathematics, Graduate School of Fundamental Science and Engineering, Waseda University, 3-4-1 Okubo, Shinjuku-ku, Tokyo, Japan email sosuke_s5@asagi.waseda.jp
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 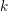$k$ be an imaginary quadratic field with 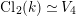$\operatorname{Cl}_{2}(k)\simeq V_{4}$. It is known that the length of the Hilbert 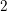$2$-class field tower is at least 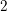$2$. Gerth (On 2-class field towers for quadratic number fields with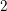$2$-class group of type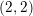$(2,2)$, Glasgow Math. J. 40(1) (1998), 63–69) calculated the density of 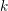$k$ where the length of the tower is 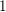$1$; that is, the maximal unramified 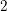$2$-extension is a 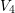$V_{4}$-extension. In this paper, we shall extend this result for generalized quaternion, dihedral, and semidihedral extensions of small degrees.

MSC classification

Primary: 11R29: Class numbers, class groups, discriminants 11R32: Galois theory 11R45: Density theorems
Type
Article
Information
Nagoya Mathematical Journal , Volume 237 , March 2020 , pp. 166 - 187
Copyright
© 2018 Foundation Nagoya Mathematical Journal  

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Benjamin, E., Lemmermeyer, F. and Snyder, C., Imaginary quadratic fields k with cyclic Cl2(k 1) , J. Number Theory 67(2) (1997), 229–245.Google Scholar
Cohn, H. and Lagarias, J. C., On the existence of fields governing the 2-invariants of the classgroup of Q(√dp) as p varies , Math. Comp. 41(164) (1983), 711–730.Google Scholar
Fröhlich, A. and Taylor, M. J., Algebra Number Theory, Cambridge Studies in Advanced Mathematics 27 , Cambridge University Press, Cambridge, 1993.Google Scholar
Furtwängler, P., Über das Verhalten der Ideale des Grundkörpers im Klassenkörper , Monatsh. Math. 27 (1916), 1–15.Google Scholar
Gerth, F. III, Counting certain number fields with prescribed l-class numbers , J. Reine Angew. Math. 337 (1982), 195–207.Google Scholar
Gerth, F. III, On 2-class field towers for quadratic number fields with 2-class group of type (2, 2) , Glasgow Math. J. 40(1) (1998), 63–69.Google Scholar
Hardy, G. H. and Wright, E. M., An Introduction to the Theory of Numbers, 4th ed. The Clarendon Press, Oxford, 1965.Google Scholar
Kisilevsky, H., Number fields with class number congruent to 4 mod 8 and Hilbert’s theorem 94 , J. Number Theory 8(3) (1976), 271–279.Google Scholar
Koch., Helmut, Introduction to Classical Mathematics. I, Mathematics and its Applications 70 , Kluwer Academic Publishers Group, Dordrecht, 1991, From the quadratic reciprocity law to the uniformization theorem, Translated and revised from the 1986 German original, Translated by John Stillwell.Google Scholar
Lagarias, J. C. and Odlyzko, A. M., “ Effective versions of the Chebotarev density theorem ”, in Algebraic number fields: L-functions and Galois properties (Proc. Sympos., Univ. Durham, Durham, 1975), Academic Press, London, 1977, 409–464.Google Scholar
Lang, S., Algebraic Number Theory, 2nd ed., Graduate Texts in Mathematics 110 , Springer, New York, 1994.Google Scholar
Lemmermeyer, F., Reciprocity Laws, Springer Monographs in Mathematics, Springer, Berlin, 2000. From Euler to Eisenstein.Google Scholar
Milovic, D., On the 16-rank of class groups of ℚ(√-8p) for p ≡-1 mod 4 , Geom. Funct. Anal. 27(4) (2017), 973–1016.Google Scholar
Rédei, L. and Reichardt, H., Die Anzahl der durch vier teilbaren Invarianten der Klassengruppe eines beliebigen quadratischen Zahlkörpers , J. Reine Angew. Math. 170 (1934), 69–74.Google Scholar
Serre, J.-P., Quelques applications du théorème de densité de Chebotarev , Publ. Math. Inst. Hautes Études Sci. 54 (1981), 323–401.Google Scholar
Stevenhagen, P., “ Ray class groups and governing fields ”, in Théorie des nombres, Publ. Math. Fac. Sci. Besançon, Univ. Franche-Comté, Besançon, 1989, 93.Google Scholar
Taussky, O., A Remark on the Class Field Tower , J. Lond. Math. Soc. (2) s1‐12(2) (1937), 82–85.Google Scholar
Washington, L. C., Introduction to Cyclotomic Fields, 2nd ed., Graduate Texts in Mathematics 83 , Springer, New York, 1997.Google Scholar
Yamamoto, Y., Divisibility by 16 of class number of quadratic fields whose 2-class groups are cyclic , Osaka J. Math. 21(1) (1984), 1–22.Google Scholar