Article contents
Eisenstein series in hyperbolic 3-space and Kronecker limit formula for biquadratic field
Published online by Cambridge University Press: 22 January 2016
Extract
Let L = 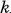 K be the composite of two imaginary quadratic fields
K be the composite of two imaginary quadratic fields 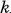 and K. Suppose that the discriminants of
and K. Suppose that the discriminants of 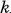 and K are relatively prime. For any primitive ray class character χ of L, we shall compute L(1, χ) for the Hecke L-function in L. We write
and K are relatively prime. For any primitive ray class character χ of L, we shall compute L(1, χ) for the Hecke L-function in L. We write 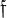 for the conductor of χ and C for the ray class modulo
for the conductor of χ and C for the ray class modulo 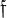 . Let c ε C be any integral ideal prime to
. Let c ε C be any integral ideal prime to 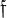 . We write
. We write 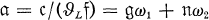 as g-module where g, n and ϑL are, respectively, the ring of integers in k, an ideal in k and the differente of L. Let
as g-module where g, n and ϑL are, respectively, the ring of integers in k, an ideal in k and the differente of L. Let 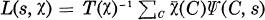 where T(χ) is the Gaussian sum and, as in (3.2),
where T(χ) is the Gaussian sum and, as in (3.2),
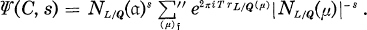
- Type
- Research Article
- Information
- Copyright
- Copyright © Editorial Board of Nagoya Mathematical Journal 1989
References
- 1
- Cited by


