No CrossRef data available.
Published online by Cambridge University Press: 22 January 2016
Let 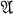 denote a non-compact parabolic Riemann surface, and let
denote a non-compact parabolic Riemann surface, and let 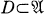 be compact and such that each frontier point of D is contained in a continuum that is also contained in D.
be compact and such that each frontier point of D is contained in a continuum that is also contained in D.