Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-13T06:43:11.870Z Has data issue: false hasContentIssue false
  • English
  • Français

Finiteness of Entire Functions Sharing a Finite Set

Published online by Cambridge University Press:  11 January 2016

Hirotaka Fujimoto
Hirotaka Fujimoto*
Affiliation:
KOKUCHU-KAI 6-19-18, Ichinoe Edogawaku, Tokyo 132-0024, Japan, h_fujimoto@kokuchukai.or.jp
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For a finite set S = {a1,…, aq}, consider the polynomial PS(w) = (w – a1)(w – a2) … (w – aq) and assume that 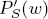has distinct k zeros. Suppose that PS(w) is a uniqueness polynomial for entire functions, namely that, for any nonconstant entire functions ɸ and ψ, the equality PS(ɸ) = cPS(ψ) implies ɸ = ψ, where c is a nonzero constant which possibly depends on ɸ and ψ. Then, under the condition q > k + 2, we prove that, for any given nonconstant entire function g, there exist at most (2q-2)/(q – k – 2) nonconstant entire functions f with f*(S) = g*(S), where f*(S) denotes the pull-back of S considered as a divisor. Moreover, we give some sufficient conditions of uniqueness polynomials for entire functions.

Keywords

30D35
Type
Research Article
Information
Nagoya Mathematical Journal , Volume 185 , 2007 , pp. 111 - 122
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 2007

References

[1] Fujimoto, H., On uniqueness of meromorphic functions sharing finite sets, Amer. J. Math., 122 (2000), 1175 – 1203.Google Scholar
[2] Fujimoto, H., On uniqueness polynomials for meromorphic functions, Nagoya Math. J., 170 (2003), 33 – 46.CrossRefGoogle Scholar
[3] Yamanoi, K., The second main theorem for small functions and related problems, Acta Math., 192 (2004), 225 – 299.Google Scholar