Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-26T07:05:45.410Z Has data issue: false hasContentIssue false
  • English
  • Français

GORENSTEIN PROJECTIVE OBJECTS IN FUNCTOR CATEGORIES

Part of: Homological algebra Homological methods Abelian categories

Published online by Cambridge University Press:  26 December 2018

SONDRE KVAMME Open the ORCID record for SONDRE KVAMME [Opens in a new window]
SONDRE KVAMME*
Affiliation:
Laboratoire de Mathématiques d’Orsay, Univ. Paris-Sud, CNRS, Université Paris-Saclay, 91405 Orsay, France email sondre.kvamme@u-psud.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 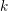$k$ be a commutative ring, let 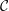${\mathcal{C}}$ be a small, 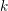$k$-linear, Hom-finite, locally bounded category, and let 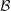${\mathcal{B}}$ be a 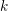$k$-linear abelian category. We construct a Frobenius exact subcategory 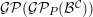${\mathcal{G}}{\mathcal{P}}({\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{B}}^{{\mathcal{C}}}))$ of the functor category 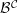${\mathcal{B}}^{{\mathcal{C}}}$, and we show that it is a subcategory of the Gorenstein projective objects 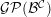${\mathcal{G}}{\mathcal{P}}({\mathcal{B}}^{{\mathcal{C}}})$ in 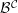${\mathcal{B}}^{{\mathcal{C}}}$. Furthermore, we obtain criteria for when 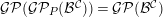${\mathcal{G}}{\mathcal{P}}({\mathcal{G}}{\mathcal{P}}_{P}({\mathcal{B}}^{{\mathcal{C}}}))={\mathcal{G}}{\mathcal{P}}({\mathcal{B}}^{{\mathcal{C}}})$. We show in examples that this can be used to compute 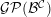${\mathcal{G}}{\mathcal{P}}({\mathcal{B}}^{{\mathcal{C}}})$ explicitly.

MSC classification

Primary: 18E10: Exact categories, abelian categories 18G25: Relative homological algebra, projective classes 16E65: Homological conditions on rings (generalizations of regular, Gorenstein, Cohen-Macaulay rings, etc.)
Type
Article
Information
Nagoya Mathematical Journal , Volume 240 , December 2020 , pp. 1 - 41
Check for updates
Copyright
© 2018 Foundation Nagoya Mathematical Journal

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

This is part of the authors PhD thesis. The author thanks Jan Geuenich and Julian Külshammer for helpful comments on a previous version of this paper, and the anonymous referee for useful suggestions and comments. The work was made possible by the funding provided by the Bonn International Graduate School in Mathematics.

References

Auslander, M. and Bridger, M., Stable Module Theory, Memoirs of the American Mathematical Society 94, American Mathematical Society, Providence, RI, 1969.10.1090/memo/0094Google Scholar
Auslander, M. and Buchweitz, R.-O., The homological theory of maximal Cohen-Macaulay approximations, Mém. Soc. Math. Fr. (N.S.) 38 (1989), 5–37; Colloque en l’honneur de Pierre Samuel (Orsay, 1987).Google Scholar
Avramov, L. L. and Martsinkovsky, A., Absolute, relative, and Tate cohomology of modules of finite Gorenstein dimension, Proc. Lond. Math. Soc. (3) 85(2) (2002), 393–440.10.1112/S0024611502013527Google Scholar
Barr, M. and Beck, J., “Homology and standard constructions”, in Sem. on Triples and Categorical Homology Theory (ETH, Zürich, 1966/67), Springer, Berlin, 1969, 245–335.10.1007/BFb0083087Google Scholar
Beligiannis, A., The homological theory of contravariantly finite subcategories: Auslander-Buchweitz contexts, Gorenstein categories and (co-)stabilization, Comm. Algebra 28(10) (2000), 4547–4596.10.1080/00927870008827105Google Scholar
Beligiannis, A., Cohen-Macaulay modules, (co)torsion pairs and virtually Gorenstein algebras, J. Algebra 288(1) (2005), 137–211.10.1016/j.jalgebra.2005.02.022Google Scholar
Beligiannis, A., On algebras of finite Cohen-Macaulay type, Adv. Math. 226(2) (2011), 1973–2019.10.1016/j.aim.2010.09.006Google Scholar
Beligiannis, A. and Krause, H., Thick subcategories and virtually Gorenstein algebras, Illinois J. Math. 52(2) (2008), 551–562.10.1215/ijm/1248355349Google Scholar
Beligiannis, A. and Reiten, I., Homological and homotopical aspects of torsion theories, Mem. Amer. Math. Soc. 188(883) (2007), viii+207.Google Scholar
Bennis, D. and Mahdou, N., Strongly Gorenstein projective, injective, and flat modules, J. Pure Appl. Algebra 210(2) (2007), 437–445.10.1016/j.jpaa.2006.10.010Google Scholar
Bühler, T., Exact categories, Expo. Math. 28(1) (2010), 1–69.10.1016/j.exmath.2009.04.004Google Scholar
Dell’Ambrogio, I., Stevenson, G. and Stovicek, J., Gorenstein homological algebra and universal coefficient theorems, Math. Z. 287(3–4) (2017), 1109–1155.10.1007/s00209-017-1862-7Google Scholar
Enochs, E., Estrada, S. and Garcia-Rozas, J. R., Gorenstein categories and Tate cohomology on projective schemes, Math. Nachr. 281(4) (2008), 525–540.10.1002/mana.200510622Google Scholar
Enochs, E., Estrada, S. and Garcia-Rozas, J. R., Injective representations of infinite quivers. Applications, Canad. J. Math. 61(2) (2009), 315–335.10.4153/CJM-2009-016-2Google Scholar
Enochs, E. E. and Jenda, O. M. G., Gorenstein injective and projective modules, Math. Z. 220(4) (1995), 611–633.10.1007/BF02572634Google Scholar
Enochs, E. E. and Jenda, O. M. G., Relative Homological Algebra. Volume 1, extended edn, De Gruyter Expositions in Mathematics 30, Walter de Gruyter GmbH & Co., KG, Berlin, 2011.Google Scholar
Enochs, E. E. and Jenda, O. M. G., Relative Homological Algebra. Volume 2, De Gruyter Expositions in Mathematics 54, Walter de Gruyter GmbH & Co., KG, Berlin, 2011.Google Scholar
Eshraghi, H., Hafezi, R. and Salarian, S., Total acyclicity for complexes of representations of quivers, Comm. Algebra 41(12) (2013), 4425–4441.10.1080/00927872.2012.701682Google Scholar
Holm, H., Gorenstein homological dimensions, J. Pure Appl. Algebra 189(1–3) (2004), 167–193.10.1016/j.jpaa.2003.11.007Google Scholar
Henrik, H. and Jørgensen, P., Cotorsion pairs in categories of quiver representations, Kyoto J. Math., to appear, preprint, 2016, arXiv:1604.01517.Google Scholar
Hu, W., Luo, X.-H., Xiong, B.-L. and Zhou, G., Gorenstein projective bimodules via monomorphism categories and filtration categories, J. Pure Appl. Algebra 223(3) (2019), 1014–1039.10.1016/j.jpaa.2018.05.012Google Scholar
Huang, Z., Proper resolutions and Gorenstein categories, J. Algebra 393 (2013), 142–169.10.1016/j.jalgebra.2013.07.008Google Scholar
Jensen, B. T., King, A. D. and Su, X., A categorification of Grassmannian cluster algebras, Proc. Lond. Math. Soc. (3) 113(2) (2016), 185–212.10.1112/plms/pdw028Google Scholar
Jørgensen, P., Existence of Gorenstein projective resolutions and Tate cohomology, J. Eur. Math. Soc. (JEMS) 9(1) (2007), 59–76.10.4171/JEMS/72Google Scholar
Jørgensen, P. and Kato, K., Symmetric Auslander and bass categories, Math. Proc. Cambridge Philos. Soc. 150(2) (2011), 227–240.10.1017/S0305004110000629Google Scholar
Jørgensen, P. and Zhang, J. J., Gourmet’s guide to Gorensteinness, Adv. Math. 151(2) (2000), 313–345.10.1006/aima.1999.1897Google Scholar
Kelly, G. M., Basic concepts of enriched category theory, Repr. Theory Appl. Categ. 10 (2005), vi+137, Reprint of the 1982 original [Cambridge University Press, Cambridge; MR0651714].Google Scholar
Kvamme, S., A generalization of the Nakayama functor, preprint, 2017, arXiv:1611.01654v2, pp. 1–38.Google Scholar
Luo, X.-H. and Zhang, P., Monic representations and Gorenstein-projective modules, Pacific J. Math. 264(1) (2013), 163–194.10.2140/pjm.2013.264.163Google Scholar
Luo, X.-H. and Zhang, P., Separated monic representations I: Gorenstein-projective modules, J. Algebra 479 (2017), 1–34.10.1016/j.jalgebra.2017.01.038Google Scholar
Mac Lane, S., Categories for the Working Mathematician, 2nd edn, Graduate Texts in Mathematics 5, Springer, New York, 1998.Google Scholar
Nájera Chávez, A., On Frobenius (completed) orbit categories, Algebr. Represent. Theory 20(4) (2017), 1007–1027.10.1007/s10468-017-9672-5Google Scholar
Oberst, U. and Röhrl, H., Flat and coherent functors, J. Algebra 14 (1970), 91–105.10.1016/0021-8693(70)90136-5Google Scholar
Popescu, N., Abelian Categories with Applications to Rings and Modules, London Mathematical Society Monographs 3, Academic Press, London–New York, 1973.Google Scholar
Pressland, M., Internally Calabi–Yau algebras and cluster-tilting objects, Math. Z. 287(1–2) (2017), 555–585.10.1007/s00209-016-1837-0Google Scholar
Shen, D., A description of Gorenstein projective modules over the tensor products of algebras, preprint, 2016, arXiv:1602.00116.Google Scholar
Stovicek, J., Derived equivalences induced by big cotilting modules, Adv. Math. 263 (2014), 45–87.10.1016/j.aim.2014.06.007Google Scholar
Yang, X. and Liu, Z., Gorenstein projective, injective, and flat complexes, Comm. Algebra 39(5) (2011), 1705–1721.10.1080/00927871003741497Google Scholar