No CrossRef data available.
Article contents
The Hecke algebra on the cohomology of Γ0 (p0)
Published online by Cambridge University Press: 22 January 2016
Extract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Let p0 be a prime, p0 > 3 and Γ0(p0), Γ1(p0) as usual, the congruence subgroups of Γ = PSL2(ℤ).
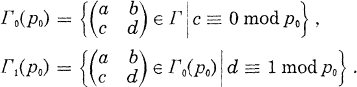
- Type
- Research Article
- Information
- Copyright
- Copyright © Editorial Board of Nagoya Mathematical Journal 1991
References
[AS]
Ash, A. and Stevens, G., Cohomology of arithmetic groups and congruences between systems of Hecke eigenvalues, J. reine angew. Math., 356 (1986), 192–220.Google Scholar
[Hab]
Haberland, K., Perioden von Modulformen einer Variabler und Gruppenkohomologie I, II, III, Math. Nachr., 112 (1983), 245–315.CrossRefGoogle Scholar
[Rib]
Ribet, K. A., Galois representations attached to eigenform with nebentypus, in: Lecture Notes in Math., 601, Springer Verlag.Google Scholar
[Shi]
Shimura, G., On elliptic curves with complex multiplication as factor of the Jacobians of modular function fields, Nagoya Math. J., 43 (1971), 199–208.Google Scholar
[Wan]
Wang, X.-D., Die Eisensteinklasse in H
1(SL
2(Z), Mn
(Z)) und die Arithmetik spezieller Werte von L-Funktionen, Bonner Math. Schriften, 20.2, Bonn (1989).Google Scholar


