Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Vostokov, S. V.
1981.
Normal basis for an ideal in a local ring.
Journal of Soviet Mathematics,
Vol. 17,
Issue. 2,
p.
1755.
Erez, B
1988.
The Galois structure of the trace form in extensions of odd prime degree.
Journal of Algebra,
Vol. 118,
Issue. 2,
p.
438.
1989.
Topics in Field Theory.
Vol. 155,
Issue. ,
p.
477.
Byott, Nigel
1991.
On Galois isomorphisms between ideals in extensions of local fields.
Manuscripta Mathematica,
Vol. 73,
Issue. 1,
p.
289.
Elder, G. Griffith
and
Madan, Manohar L.
1995.
Galois module structure of the integers in weakly ramified extensions.
Archiv der Mathematik,
Vol. 64,
Issue. 2,
p.
117.
Byott, Nigel P.
1997.
Galois structure of ideals in wildly ramified abelian p-extensions of a p-adic field, and some applications.
Journal de théorie des nombres de Bordeaux,
Vol. 9,
Issue. 1,
p.
201.
Elder, G. Griffith
2002.
On Galois structure of the integers in cyclic extensions of local number fields.
Journal de théorie des nombres de Bordeaux,
Vol. 14,
Issue. 1,
p.
113.
Bergeron, Nicolas
Şengün, Mehmet Haluk
and
Venkatesh, Akshay
2016.
Torsion homology growth and cycle complexity of arithmetic manifolds.
Duke Mathematical Journal,
Vol. 165,
Issue. 9,
Tsang, Cindy (Sin Yi)
2016.
On the Galois module structure of the square root of the inverse different in abelian extensions.
Journal of Number Theory,
Vol. 160,
Issue. ,
p.
759.
Tsang, Cindy (Sin Yi)
2017.
Realizable Classes and Embedding Problems.
Journal de théorie des nombres de Bordeaux,
Vol. 29,
Issue. 2,
p.
647.
Keating, Kevin
2020.
Galois scaffolds and semistable extensions.
Journal of Number Theory,
Vol. 207,
Issue. ,
p.
110.
Del Corso, Ilaria
Ferri, Fabio
and
Lombardo, Davide
2022.
How far is an extension of p-adic fields from having a normal integral basis?.
Journal of Number Theory,
Vol. 233,
Issue. ,
p.
158.
Ferrara, Joseph
Green, Nathan
Higgins, Zach
and
Popescu, Cristian D.
2022.
An equivariant Tamagawa number formula for Drinfeld modules and applications.
Algebra & Number Theory,
Vol. 16,
Issue. 9,
p.
2215.
Berger, Tobias
and
Klosin, Krzysztof
2023.
𝑅=𝑇 theorems for weight one modular forms.
Transactions of the American Mathematical Society,

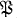 ; the collection of ideals
; the collection of ideals 