No CrossRef data available.
Article contents
Irreducibility of some unitary representations of the Poincaré group with respect to the Poincaré subsemigroup, III
Published online by Cambridge University Press: 22 January 2016
Extract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
The aim of this paper is to prove that irreducible unitary representations 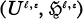 of the Poincaré group P = R 4 × SSL(2, C) are reducible as the representations of the Poincaré subsemigroup P + = V + × SSL(2, C) with
of the Poincaré group P = R 4 × SSL(2, C) are reducible as the representations of the Poincaré subsemigroup P + = V + × SSL(2, C) with 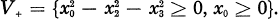
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Editorial Board of Nagoya Mathematical Journal 1982
References
[1]
Angelopoulos, E., Reduction on the Lorentz subgroup of UIR’s of the Poincaré group induced by semisimple little group, Math. Phys., 15 (1974), 155–165.CrossRefGoogle Scholar
[2]
Coddington, E. A. and Levinson, N., Theory of differential equations, McGraw-Hill, 1955.Google Scholar
[4]
Itatsu, S. and Kaneta, H., Spectral matrices for first and second order self-adjoint ordinary differential operators with long range potentials, Funkcialaj Ekvacioj, 24, no. 1 (1981), 23–45.Google Scholar
[5]
Itatsu, S. and Kaneta, H., Spectral matrices for first and second order self-adjoint ordinary differential operators with short range potentials, Funkcialaj Ekvacioj, 24, no. 2 (1981), 167–186.Google Scholar
[6]
Kaneta, H., Irreducibility of some unitary representations of the Poincaré group with respect to the Poincaré subsemigroup, I, Nagoya Math. J., 78 (1980), 113–136.CrossRefGoogle Scholar
[7]
Kaneta, H., Irreducibility of some unitary representations of the Poincaré group with respect to the Poincaré subsemigroup, II, Nagoya Math. J., 87 (1982), 147–174.CrossRefGoogle Scholar
[9]
Lions, J. L. and Magenes, E., Problèmes aux limites non-homogénes et applications, Vol. 1, Dunod, 1968.Google Scholar
[10]
Mackey, G. M., Induced representations of locally compact groups I, Ann. of Math.
55 (1952),101–139.CrossRefGoogle Scholar
[11]
Mukunda, N., Zero-mass representations of the Poincaré group in an 0(3, 1) basis, J. Math. Phys., 9 (1968), 532–536.CrossRefGoogle Scholar
[12]
Neumark, M. A., Lineare Darstellungen der Loretz gruppe, VED Deutsher Verlag der Wissenshahten, 1963.Google Scholar
[13]
Vilenkin, N., Special functions and the theory of group representations, AMS Translation Monographs
22, 1968.Google Scholar

