Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Obata, Nobuaki
1988.
A note on certain permutation groups in the infinite dimensional rotation group.
Nagoya Mathematical Journal,
Vol. 109,
Issue. ,
p.
91.
Brüning, Erwin
and
Nagamachi, Shigeaki
1989.
Hyperfunction quantum field theory: Basic structural results.
Journal of Mathematical Physics,
Vol. 30,
Issue. 10,
p.
2340.
Kuo, Hui-Hsiung
Obata, Nobuaki
and
Saitô, Kimiaki
1990.
Lévy Laplacian of generalized functions on a nuclear space.
Journal of Functional Analysis,
Vol. 94,
Issue. 1,
p.
74.
Saito, Kimiaki
1991.
Ito’s formula and Levy’s Laplacian II.
Nagoya Mathematical Journal,
Vol. 123,
Issue. ,
p.
153.
Hida, Takeyuki
Obata, Nobuaki
and
Saitô, Kimiaki
1992.
Infinite dimensional rotations and Laplacians in terms of white noise calculus.
Nagoya Mathematical Journal,
Vol. 128,
Issue. ,
p.
65.
di Accarde, Luigi
Gibilisco, Paolo
and
Volovich, Igor V.
1993.
The Lévy laplacian and the Yang-Mills equations.
Rendiconti Lincei,
Vol. 4,
Issue. 3,
p.
201.
Hida, Takeyuki
1993.
Stochastic Processes.
p.
131.
Saitô, Kimiaki
1998.
A C0-Group Generated by the Lévy Laplacian II.
Infinite Dimensional Analysis, Quantum Probability and Related Topics,
Vol. 01,
Issue. 03,
p.
425.
Saitô, Kimiaki
1998.
A (Co)-group generated by the lévy laplacian.
Stochastic Analysis and Applications,
Vol. 16,
Issue. 3,
p.
567.
CHUNG, DONG MYUNG
JI, UN CIG
and
SAITÔ, KIMIAKI
1999.
CAUCHY PROBLEMS ASSOCIATED WITH THE LÉVY LAPLACIAN IN WHITE NOISE ANALYSIS.
Infinite Dimensional Analysis, Quantum Probability and Related Topics,
Vol. 02,
Issue. 01,
p.
131.
Koshkin, S. V.
2000.
Differential Operators and Related Topics.
p.
187.
Saitô, Kimiaki
2000.
A Stochastic Process Generated by the Lévy Laplacian.
Acta Applicandae Mathematica,
Vol. 63,
Issue. 1-3,
p.
363.
Liu, Kai
and
Chen, Anyue
2001.
A Class of generalized Lévy Laplacians in infinite dimensional calculus.
Israel Journal of Mathematics,
Vol. 124,
Issue. 1,
p.
157.
Saitô, Kimiaki
2001.
The Lévy Laplacian and stable processes.
Chaos, Solitons & Fractals,
Vol. 12,
Issue. 14-15,
p.
2865.
Saitô, Kimiaki
2001.
Recent Developments in Infinite-Dimensional Analysis and Quantum Probability.
p.
363.
KUO, HUI-HSIUNG
OBATA, NOBUAKI
and
SAITÔ, KIMIAKI
2002.
DIAGONALIZATION OF THE LÉVY LAPLACIAN AND RELATED STABLE PROCESSES.
Infinite Dimensional Analysis, Quantum Probability and Related Topics,
Vol. 05,
Issue. 03,
p.
317.
SAITÔ, Kimiaki
2009.
A Gauss-Poisson Correspondence and the Lévy Laplacian.
Interdisciplinary Information Sciences,
Vol. 15,
Issue. 3,
p.
431.
BARHOUMI, ABDESSATAR
OUERDIANE, HABIB
and
RGUIGUI, HAFEDH
2012.
STOCHASTIC HEAT EQUATION ON ALGEBRA OF GENERALIZED FUNCTIONS.
Infinite Dimensional Analysis, Quantum Probability and Related Topics,
Vol. 15,
Issue. 04,
p.
1250026.
ACCARDI, LUIGI
JI, UN CIG
and
SAITÔ, KIMIAKI
2013.
THE EXOTIC (HIGHER ORDER LÉVY) LAPLACIANS GENERATE THE MARKOV PROCESSES GIVEN BY DISTRIBUTION DERIVATIVES OF WHITE NOISE.
Infinite Dimensional Analysis, Quantum Probability and Related Topics,
Vol. 16,
Issue. 03,
p.
1350020.
Accardi, Luigi
Hasegawa, Ai
Ji, Un Cig
and
Saitô, Kimiaki
2020.
White noise delta functions and infinite-dimensional Laplacians.
Infinite Dimensional Analysis, Quantum Probability and Related Topics,
Vol. 23,
Issue. 04,
p.
2050028.

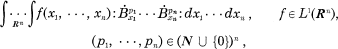
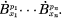 denotes the renormalization of
denotes the renormalization of 