Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-10T13:45:05.515Z Has data issue: false hasContentIssue false
  • English
  • Français

JET SCHEMES OF QUASI-ORDINARY SURFACE SINGULARITIES

Part of: Birational geometry Surfaces and higher-dimensional varieties

Published online by Cambridge University Press:  20 September 2019

HELENA COBO  and
HUSSEIN MOURTADA
HELENA COBO
Affiliation:
Departamento de Álgebra, Universidad de Sevilla, Spain email helenacobo@gmail.com
HUSSEIN MOURTADA
Affiliation:
Institut de Mathématiques de Jussieu-Paris Rive Gauche, Université Paris 7, Bâtiment Sophie Germain, 75013 Paris, France email hussein.mourtada@imj-prg.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

We describe the irreducible components of the jet schemes with origin in the singular locus of a two-dimensional quasi-ordinary hypersurface singularity. A weighted graph is associated with these components and with their embedding dimensions and their codimensions in the jet schemes of the ambient space. We prove that the data of this weighted graph is equivalent to the data of the topological type of the singularity. We also determine a component of the jet schemes (equivalent to a divisorial valuation on 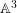$\mathbb{A}^{3}$), that computes the log-canonical threshold of the singularity embedded in 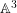$\mathbb{A}^{3}$. This provides us with pairs 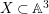$X\subset \mathbb{A}^{3}$ whose log-canonical thresholds are not computed by monomial divisorial valuations. Note that for a pair 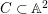$C\subset \mathbb{A}^{2}$, where 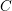$C$ is a plane curve, the log-canonical threshold is always computed by a monomial divisorial valuation (in suitable coordinates of 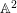$\mathbb{A}^{2}$).

MSC classification

Primary: 14E18: Arcs and motivic integration 14J17: Singularities
Type
Article
Information
Nagoya Mathematical Journal , Volume 242 , June 2021 , pp. 77 - 164
Check for updates
Copyright
© 2019 Foundation Nagoya Mathematical Journal

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abhyankar, S. S., On the ramification of algebraic functions, Amer. J. Math. 77 (1955), 575–592.Google Scholar
Aprodu, M. and Naie, D., Enriques diagrams and log-canonical thresholds of curves on smooth surfaces, Geom. Dedicata 146 (2010), 43–66.Google Scholar
Artal Bartolo, E., Cassou-Noguès, Pi., Luengo, I. and Melle Hernández, A., Quasi-ordinary power series and their zeta functions, Mem. Amer. Math. Soc. 178(841) (2005), 1–85.Google Scholar
Artal Bartolo, E., Cassou-Noguès, Pi., Luengo, I. and Melle-Hernández, A., “On the log-canonical threshold for germs of plane curves”, in Singularities I, Contemp. Math. 474, Amer. Math. Soc., Providence, RI, 2008, 1–14.Google Scholar
Assi, A., Irreducibility criterion for quasi-ordinary polynomials, J. Singul. 4 (2012), 23–34.Google Scholar
Ban, C. and McEwan, L., Canonical resolution of a quasi-ordinary surface singularity, Canad. J. Math. 52(6) (2000), 1149–1163.Google Scholar
Ban, C. and McEwan, L., “Simultaneous resolution of equisingular quasi-ordinary singularities”, in Singularities in Algebraic and Analytic Geometry (San Antonio, TX, 1999), Contemp. Math. 266, Amer. Math. Soc., Providence, RI, 2000, 65–75.Google Scholar
Budur, N., González Pérez, P. D. and González Villa, M., Log-canonical thresholds of quasi-ordinary hypersurfaces singularities, Proc. Amer. Math. Soc. 140 (2012), 4075–4083.Google Scholar
Cobo Pablos, H. and González Pérez, P. D., Geometric motivic Poincaré series of quasi-ordinary hypersurfaces, Math. Proc. Cambridge Philos. Soc. 149(01) (2010), 49–74.Google Scholar
Denef, J. and Loeser, F., Germs of arcs on singular algebraic varieties and motivic integration, Invent. Math. 135(1) (1999), 201–232.Google Scholar
Denef, J. and Loeser, F., “Geometry on arc spaces of algebraic varieties”, in European Congress of Mathematics, Vol. I (Barcelona, 2000), Progr. Math. 201, Birkhäuser, Basel, 2001, 327–348.Google Scholar
Docampo, R., Arcs on determinantal varieties, Trans. Amer. Math. Soc. 365(5) (2013), 2241–2269.Google Scholar
Ein, L. and Mustaţa, M., “Jet Schemes and Singularities”, in Algebraic geometry-Seattle 2005, Proc. Sympos. Pure Math. 80, Part 2, Amer. Math. Soc., Providence, RI, 2009, 505–546.Google Scholar
García Barroso, E. and Gwodziewicz, J., Quasi-ordinary singularities: tree model, discriminant and irreducibility, Int. Math. Res. Not. 14 (2015), 5783–5805.Google Scholar
Gau, Y.-N., Embedded Topological classification of quasi-ordinary singularities, Mem. Amer. Math. Soc. 388 (1988).Google Scholar
González Pérez, P. D., The semigroup of a quasi-ordinary hypersurface, J. Inst. Math. Jussieu 2(3) (2003), 383–399.Google Scholar
González Pérez, P. D., Toric embedded resolutions of quasi-ordinary hypersurface singularities, Ann. Inst. Fourier 53(6) (2003), 1819–1881.Google Scholar
González Pérez, P. D. and González Villa, M., Motivic Milnor fiber of a quasi-ordinary hypersurface, J. Reine Angew. Math. 687 (2014), 159–205.Google Scholar
Ishii, S., Jet schemes, arc spaces and the Nash problem, C. R. Math. Acad. Sci. Soc. R. Can. 29(1) (2007), 1–21.Google Scholar
Kiyek, K. and Micus, M., “Semigroup of a quasiordinary singularity”, Topics in Algebra, Part 2 (Warsaw, 1988), 149–156. Banach Center Publ., 26.Google Scholar
Lejeune-Jalabert, M., Mourtada, H. and Reguera, A., Jet schemes and minimal embedded desingularization of plane branches, Revista de la Real Academia de Ciencias Exactas, Físicas y Naturales. Serie A. Matemáticas 107(1) (2013), 145–157.Google Scholar
Lipman, J., Topological invariants of quasi-ordinary singularities, Mem. Amer. Math. Soc. 74(388) (1988), 1–107.Google Scholar
Lipman, J., “Equisingularity and simultaneous resolution of singularities”, in Resolution of Singularities (Obergurgl, 1997), Progr. Math. 181, Birkhäuser, Basel, 2000, 485–505.Google Scholar
Mourtada, H., Jet schemes of complex plane branches and equisingularity, Ann. Inst. Fourier 61(6) (2011), 2313–2336.Google Scholar
Mourtada, H., Jet schemes of normal toric surfaces, Bull. SMF 145(fascicule 2) (2017), 237–266.Google Scholar
Mourtada, H., “Jet schemes of rational double point surface singularities”, in Valuation Theory in Interaction, EMS Ser. Congr. Rep., Eur. Math. Soc., Zürich, 2014, 373–388.Google Scholar
Mourtada, H., Jet schemes and minimal generating sequences of divisorial valuations in dimension two, Michigan Math. J. 66(1) (2017), 155–174.Google Scholar
Mourtada, H. and Plénat, C., Jet schemes and minimal toric embedded resolutions of rational double point singularities, Comm. Algebra 46(3) (2018), 1314–1332.Google Scholar
Mustaţa, M., Singularities of pairs via jets schemes, J. Amer. Math. Soc. 15(3) (2002), 599–615.Google Scholar
Popescu-Pampu, P., On the analytical invariance of the semigroups of a quasi-ordinary hypersurface singularity, Duke Math. J. 124(1) (2004), 67–104.Google Scholar
Popescu-Pampu, P., Introduction to Jung’s method of resolution of singularities, Contemp. Math. 538 (2011), 401–432.Google Scholar
Popescu-Pampu, P., From singularities to graphs, preprint, 2018, arXiv:1808.00378.Google Scholar
Sethuraman, B. A. and Šivic, K., Jet schemes of the commuting matrix pairs scheme, Proc. Amer. Math. Soc., 137(12) (2009), 3953–3967.Google Scholar
Villamayor, O., On equiresolution and a question of Zariski, Acta Math. 185(1) (2000), 123–159.Google Scholar
Yuen, C., “Jet schemes of determinantal varieties”, in Algebra, Geometry and Their Interactions, Contemp. Math. 448, Amer. Math. Soc., 2007, 261–270.Google Scholar