Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-10T15:22:41.040Z Has data issue: false hasContentIssue false
  • English
  • Français

Lifting of supersingular points on X0 (pr) and lower bound of ramification index

Published online by Cambridge University Press:  22 January 2016

Fumiyuki Momose  and
Mahoro Shimura
Fumiyuki Momose
Affiliation:
Department of Mathematics, Chuo University, 1-13-27, Kasuga Bunkyou-ku Tokyo, 112, Japan, momose@math.chuo-u.ac.jp
Mahoro Shimura
Affiliation:
Department of Mathematics, Waseda University, 3-4-1, Okubo Shinjuku-ku Tokyo, 169-8555, Japan, shimura@gm.math.waseda.ac.jp
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let K be a finite extension of 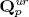(= the maximal unramified extension of Qp) of degree eK, 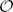its integer ring, p a rational prime and r a positive integer. If there exists a one parameter formal group defined over 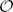whose reduction is of height 2 with a cyclic subgroup V of order pr defined over 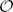, then .

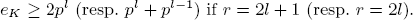We apply this result to a criterion for non-existence of Q-rational point of 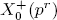. (This criterion is Momose’s theorem in [14] except for the cases p = 5 and p = 13, but our new proof does not require defining equations of modular curves except for the case p = 2.)

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 165 , March 2002 , pp. 159 - 178
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 2002

References

[1] Bercovic, V. G., The rational points on the jacobians of modular curves, Math. USSR-sb., 30 (1976), 485–500.Google Scholar
[2] Brumer, A. and Kramer, K., The rank of elliptic curves, Duke Math. J., 44 (1977), no. 4, 715–743.CrossRefGoogle Scholar
[3] Brumer, A., The rank of J0(N), Columbia University Number Theory Seminar (New York, 1992). Astèrisque no. 228 (1995), no. 3, 41–68.Google Scholar
[4] Cremona, J. E., Algorithms for modular elliptic curves, Cambridge University Press, Cambridge, 1992.Google Scholar
[5] Deigne, P. and Rapoport, M., Les schémas de modules des courbes elliptiques, vol. II of the Proceedings of the International Summer School on Modular Functions, Antwerp, 1972, Lecture Notes in Math. vol. 349, Springer (1973).Google Scholar
[6] Fricke, R., Die Elliptischen Funktionen und ihre Anwendungen, Teubner, LeipzigBerlin, 1922.Google Scholar
[7] Hasegawa, Y. and Momose, F., Rational points on X+(13r), preprint.Google Scholar
[8] Hibino, T. and Murabayashi, N., Modular equations of hyperelliptic X0(N) and an application, Acta Arith., 82 (1997), no. 3, 279–291.Google Scholar
[9] Katz, N. and Mazur, R., Arithmetic moduli of elliptic curves, Annals of Math. Studies 108, Princeton Univ. Press, 1985.Google Scholar
[10] Mazur, B., Modular curves and the Eisenstein ideal, Publ. Math. I.H.E.S., 47 (1977), 33–186.Google Scholar
[11] Mazur, B., Rational points on modular curves, Proceedings of conference on Modular functions held in Bonn, Lecture Notes in Math. vol. 601.Google Scholar
[12] Mazur, B. and Swinnerton-Dyer, P., Arithmetic of Weil curves, Invent. Math., 25 (1974), 1–61.CrossRefGoogle Scholar
[13] Momose, F., Rational points on the modular curves Xsplit(p), Compositio. Math., 52 (1984), 115–137.Google Scholar
[14] Momose, F., Rational points on the modular curves X+(pr), J. Fac. Sci. Univ. Tokyo Sect. IA, Math. 33 (1986), 441–466.Google Scholar
[15] Momose, F., Rational points on X0(37N)/(w37N), preprint.Google Scholar
[16] Poulakis, D., La courbe modulaire X0(125) et sa jacobienne, J. of Number Theory, 25 (1987), 112–131.Google Scholar
[17] Silverman, J., The Arithmetic of Elliptic Curves, SLN 106, Springer, 1986.Google Scholar
[18] Shimura, G., Introduction to the arithmetic theory of automorphic functions, Publ. Math. Soc. Japan 11, Iwanami Shoten, Tokyo-Princeton Univ. Press, Princeton, N. J., 1971.Google Scholar
[19] Tate, J., p-divisible groupes, Proceedings of a Conference on Local Fields, Driebergen, 1966, Springer, 1967, 158–183.Google Scholar
[20] Birch, B. J. and Kuyk, W., eds., Modular functions of one variable IV, Lecture Note in Math. vol. 476, Springer, 1975.Google Scholar