Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-26T07:12:00.740Z Has data issue: false hasContentIssue false
  • English
  • Français

LOCAL DUALITY FOR THE SINGULARITY CATEGORY OF A FINITE DIMENSIONAL GORENSTEIN ALGEBRA

Part of: Representation theory of rings and algebras Homological methods

Published online by Cambridge University Press:  11 March 2020

DAVE BENSON Open the ORCID record for DAVE BENSON [Opens in a new window] ,
SRIKANTH B. IYENGAR Open the ORCID record for SRIKANTH B. IYENGAR [Opens in a new window] ,
HENNING KRAUSE Open the ORCID record for HENNING KRAUSE [Opens in a new window]  and
JULIA PEVTSOVA
DAVE BENSON
Affiliation:
Institute of Mathematics, University of Aberdeen, King’s College, AberdeenAB24 3UE, Scotland, UK email d.j.benson@abdn.ac.uk
SRIKANTH B. IYENGAR
Affiliation:
Department of Mathematics, University of Utah, Salt Lake City, UT84112, USA email iyengar@math.utah.edu
HENNING KRAUSE
Affiliation:
Fakultät für Mathematik, Universität Bielefeld, 33501Bielefeld, Germany email hkrause@math.uni-bielefeld.de
JULIA PEVTSOVA
Affiliation:
Department of Mathematics, University of Washington, Seattle, WA98195, USA email pevtsova@uw.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

A duality theorem for the singularity category of a finite dimensional Gorenstein algebra is proved. It complements a duality on the category of perfect complexes, discovered by Happel. One of its consequences is an analogue of Serre duality, and the existence of Auslander–Reiten triangles for the 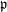$\mathfrak{p}$-local and 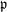$\mathfrak{p}$-torsion subcategories of the derived category, for each homogeneous prime ideal 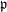$\mathfrak{p}$ arising from the action of a commutative ring via Hochschild cohomology.

MSC classification

Primary: 16G10: Representations of Artinian rings
Secondary: 16G50: Cohen-Macaulay modules 16E65: Homological conditions on rings (generalizations of regular, Gorenstein, Cohen-Macaulay rings, etc.) 16E35: Derived categories
Type
Article
Information
Nagoya Mathematical Journal , Volume 244 , December 2021 , pp. 1 - 24
Check for updates
Copyright
© 2020 Foundation Nagoya Mathematical Journal

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The second author was partly supported by the National Science Foundation grants DMS-1503044 and DMS-1700985. The fourth author was partly supported by the National Science Foundation grants DMS-1501146 and DMS-1901854.

References

Amiot, C., Sur les petites catégories triangulées, Ph.D. thesis, Universitè Paris 7, 2008.Google Scholar
Assem, I. and Skowroński, A., Iterated tilted algebras of type à n , Math. Z. 195 (1987), 269–290.CrossRefGoogle Scholar
Auslander, M., “ Functors and morphisms determined by objects ”, in Representation Theory of Algebras (Proc. Conf., Temple University, Philadelphia, PA, 1976), Lecture Notes in Pure Appl. Mathematics 37 , Dekker, New York, 1978, 1–244.Google Scholar
Auslander, M. and Buchweitz, R.-O., The homological theory of maximal Cohen–Macaulay approximations , Mém. Soc. Math. France (N.S.) 38 (1989), 5–37.CrossRefGoogle Scholar
Auslander, M. and Reiten, I., On a generalized version of the Nakayama conjecture , Proc. Amer. Math. Soc. 52 (1975), 69–74.CrossRefGoogle Scholar
Auslander, M. and Reiten, I., “ Cohen–Macaulay and Gorenstein Artin algebras ”, in Representation Theory of Finite Groups and Finite-Dimensional Algebras (Bielefeld, 1991), Progress in Mathematics 95 , Birkhäuser, Basel, 1991, 221–245.CrossRefGoogle Scholar
Benson, D. J., Iyengar, S. B. and Krause, H., Local cohomology and support for triangulated categories , Ann. Sci. Éc. Norm. Sup. (4) 41 (2008), 575–621.Google Scholar
Benson, D. J., Iyengar, S. B. and Krause, H., Stratifying triangulated categories , J. Topol. 4 (2011), 641–666.Google Scholar
Benson, D. J., Iyengar, S. B. and Krause, H., Colocalising subcategories and cosupport , J. Reine Angew. Math. 673 (2012), 161–207.Google Scholar
Benson, D. J., Iyengar, S. B., Krause, H. and Pevtsova, J., Stratification for module categories of finite group schemes , J. Amer. Math. Soc. 31 (2018), 265–302.CrossRefGoogle Scholar
Benson, D. J., Iyengar, S. B., Krause, H. and Pevtsova, J., Local duality for representations of finite group schemes , Compos. Math. 155 (2019), 424–453.CrossRefGoogle Scholar
Bondal, A. I. and Kapranov, M. M., Representable functors, Serre functors, and mutations , Izv. Akad. Nauk SSSR Ser. Mat. 53(6) (1989), 1183–1205, 1337; translation in Math. USSR-Izv. 35(3) (1990), 519–541.Google Scholar
Bruns, W. and Herzog, J., Cohen–Macaulay Rings, Revised edition, Cambridge Studies in Advanced Mathematics, 39 , Cambridge University Press, Cambridge, 1998.CrossRefGoogle Scholar
Buchweitz, R.-O., Maximal Cohen–Macaulay modules and Tate-cohomology over Gorenstein rings, Unpublished manuscript (1986, 155 pp, available at https://tspace.library.utoronto.ca/handle/1807/16682.Google Scholar
Cartan, H. and Eilenberg, S., Homological Algebra, Princeton University Press, Princeton, NJ, 1956.Google Scholar
Erdmann, K., Holloway, M., Taillefer, R., Snashall, N. and Solberg, Ø., Support varieties for selfinjective algebras , K-Theory 33 (2004), 67–87.CrossRefGoogle Scholar
Geiß, C. and Reiten, I., “ Gentle algebras are Gorenstein ”, in Representations of Algebras and Related Topics, Fields Inst. Commun. 45 , American Mathematical Society, Providence, RI, 2005, 129–133.Google Scholar
Ginzburg, V. and Kumar, S., Cohomology of quantum groups at roots of unity , Duke Math. J. 69 (1993), 179–198.CrossRefGoogle Scholar
Happel, D., On the derived category of a finite-dimensional algebra , Comment. Math. Helv. 62(3) (1987), 339–389.CrossRefGoogle Scholar
Iyengar, S. and Krause, H., Acyclicity versus total acyclicity for complexes over Noetherian rings , Doc. Math. 11 (2006), 207–240.Google Scholar
Mastnak, M., Pevtsova, J., Schaunberg, P. and Witherspoon, S., Cohomology of finite dimensional pointed Hopf algebras , Proc. Lond. Math. Soc. 100 (2010), 377–404.CrossRefGoogle Scholar
Orlov, D. O., Triangulated categories of singularities and D-branes in Landau–Ginzburg models, (Russian) translated from Tr. Mat. Inst. Steklova 246 (2004), Algebr. Geom. Metody, Svyazi i Prilozh., 240–262, Proc. Steklov Inst. Math. 246 (2004), 227–248.Google Scholar
Ringel, C. M. and Zhang, P., Representations of quivers over the algebra of dual numbers , J. Algebra 475 (2017), 327–360.CrossRefGoogle Scholar
Solberg, Ø., “ Support varieties for modules and complexes ”, in Trends in Representation Theory of Algebras and Related Topics, Contemporary Mathematics 406 , American Mathematical Society, Providence, RI, 2006, 239–270.CrossRefGoogle Scholar
Zaks, A., Injective dimension of semi-primary rings , J. Algebra 13 (1969), 73–86.CrossRefGoogle Scholar