Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Dunn, Alexander
2018.
Uniform bounds for sums of Kloosterman sums of half integral weight.
Research in Number Theory,
Vol. 4,
Issue. 4,
Boylan, Matthew
2021.
-operators and congruences for Shimura images.
Journal of Number Theory,
Vol. 220,
Issue. ,
p.
75.
Ahlgren, Scott
Allen, Patrick
and
Tang, Shiang
2022.
Congruences like Atkin’s for the partition function.
Transactions of the American Mathematical Society, Series B,
Vol. 9,
Issue. 33,
p.
1044.
Dicks, Robert
2023.
Congruence relations for r-colored partitions.
Journal of Number Theory,
Vol. 249,
Issue. ,
p.
377.
Raum, Martin
2023.
Relations among Ramanujan-type congruences II: Ramanujan-type congruences in half-integral weights.
Forum Mathematicum,
Vol. 0,
Issue. 0,
Ahlgren, Scott
Andersen, Nickolas
and
Dicks, Robert
2024.
The Shimura lift and congruences for modular forms with the eta multiplier.
Advances in Mathematics,
Vol. 447,
Issue. ,
p.
109655.
Williams, Clayton
2025.
Hecke relations for eta multipliers and congruences for higher-order smallest parts functions.
Journal of Number Theory,
Vol. 277,
Issue. ,
p.
325.

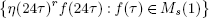
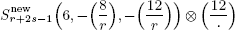
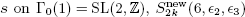 is the space of newforms of weight 2
is the space of newforms of weight 2