Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-26T07:20:22.112Z Has data issue: false hasContentIssue false
  • English
  • Français

Multiple zeta values, poly-Bernoulli numbers, and related zeta functions

Published online by Cambridge University Press:  22 January 2016

Tsuneo Arakawa  and
Masanobu Kaneko
Tsuneo Arakawa
Affiliation:
Department of Mathematics, Rikkyo University, Ikebukuro, Tokyo 171-8501, Japan, tsuneo@rkmath.rikkyo.ac.jp
Masanobu Kaneko
Affiliation:
Graduate School of Mathematics, Kyushu University, Fukuoka, 812-8581, Japan, mkaneko@math.kyushu-u.ac.jp
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

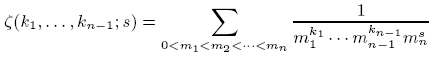We study the function and show that the poly-Bernoulli numbers introduced in our previous paper are expressed as special values at negative arguments of certain combinations of these functions. As a consequence of our study, we obtain a series of relations among multiple zeta values.

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 153 , 1999 , pp. 189 - 209
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1999

References

[A] Arnold, V. I., The Vassiliev theory of discriminants and knots, in ECM volume, Progress in Math., 120 (1994), 3–29.Google Scholar
[BBB] Borwein, J. M., Bradley, D. M. and Broadhurst, D. J., Evaluations of k-fold Euler/Zagier sums: a compendium of results for arbitrary k, hep-th/9611004.CrossRefGoogle Scholar
[BBG] Borwein, D., Borwein, J. M. and Girgensohn, R., Explicit evaluation of Euler sums, Proc. Edin. Math. Soc, 38 (1995), 277–294.Google Scholar
[Br] Broadhurst, D. J., Conjectured enumeration of irreducible multiple zeta values, from knots and Feynman diagrams, hep-th/9612012.Google Scholar
[C] Carlitz, L., Some theorems on Bernoulli numbers of higher order, Pacific J. Math., 2 (1952), 127–139.Google Scholar
[H] Hoffman, M., Multiple harmonic series, Pacific J. Math., 152 (1992), 275–290.Google Scholar
[HWN] Huard, J. G., Williams, K. S. and Nan-Yue, Z., On Tornheim’s double series, Acta Arithmetica, 65-2 (1996), 105–117.CrossRefGoogle Scholar
[J] Jordan, Ch., Calculus of Finite Differences, Chelsea Publ. Co., New York, 1950.Google Scholar
[Ka] Kaneko, M., Poly-Bernoulli numbers, J. Th. Nombre Bordeaux, 9 (1997), 199–206.Google Scholar
[LM] Le, T. Q. T. and Murakami, J., Kontsevich’s integral for the Homfly polynomial and relations between values of multiple zeta functions, Topology and its Appli cations, 62 (1995), 193–206.Google Scholar
[L] Lewin, L., Polylogarithms and Associated Functions, Tata Institute, Bombay, 1980.Google Scholar
[O] Ohno, Y., A generalization of the duality and the sum formula on the multiple zeta values, J. Number Th., 74 (1999), 39–43.CrossRefGoogle Scholar
[S] Siegel, C. L., Advanced Analytic Number Theory, Chelsea Publ. Co., New York, 1950.Google Scholar
[Z] Zagier, D., Multiple zeta values, in preparation.Google Scholar
[Z2] Zagier, D., Values of zeta functions and their applications, in ECM volume, Progress in Math., 120 (1994), 497–512.Google Scholar
[Z3] Zagier, D., Zetafunktionen und quadratische Körper, Springer, 1981.Google Scholar