Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Kawazumi, Nariya
2002.
Weierstrass points and Morita–Mumford classes on hyperelliptic mapping class groups.
Topology and its Applications,
Vol. 125,
Issue. 3,
p.
363.
Galatius, Soren
Madsen, Ib
and
Tillmann, Ulrike
2006.
Divisibility of the stable Miller-Morita-Mumford classes.
Journal of the American Mathematical Society,
Vol. 19,
Issue. 4,
p.
759.
Pappas, Georgios
2007.
Integral Grothendieck–Riemann–Roch theorem.
Inventiones mathematicae,
Vol. 170,
Issue. 3,
p.
455.
AKITA, TOSHIYUKI
and
KAWAZUMI, NARIYA
2008.
Integral Riemann–Roch formulae for cyclic subgroups of mapping class groups.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 144,
Issue. 2,
p.
411.
Madsen, Ib
2010.
An integral Riemann–Roch theorem for surface bundles.
Advances in Mathematics,
Vol. 225,
Issue. 6,
p.
3229.

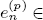
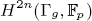 of the mapping class group Γ
of the mapping class group Γ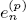 is nilpotent if
is nilpotent if 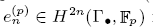 is proved to be nontrivial and not nilpotent if
is proved to be nontrivial and not nilpotent if 