No CrossRef data available.
Article contents
On Associative Compositions in Finite Nilpotent Groups
Published online by Cambridge University Press: 22 January 2016
Extract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Let
(1) 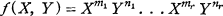
be a word in two variables X, Y, i.e. an element in the free group F2 on two generators X, Y. Let us say that f defines an associative composition for a group G if for arbitrary elements a, b, c in G we have
(2) 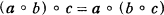
where a ° b is defined by
(3) 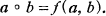
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Editorial Board of Nagoya Mathematical Journal 1954
References
1 Iwasawa, K., Einige Satze uber freie Gruppen, Proc. Imp. Acad. Japan, 19 (1943), pp. 272–274 Google Scholar.
2 Note that ![]() is a central subgroup of
is a central subgroup of ![]() Then for every a, b in G, c, d in
Then for every a, b in G, c, d in ![]() we have
we have ![]() (cf. H. Zassenhaus, Lehrbuch der Gruppentheorie, S. 57). The assertion is then completed by induction on i.
(cf. H. Zassenhaus, Lehrbuch der Gruppentheorie, S. 57). The assertion is then completed by induction on i.

