Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Peng, Chia-Kuei
and
Terng, Chuu-Lian
1983.
The scalar curvature of minimal hypersurfaces in spheres.
Mathematische Annalen,
Vol. 266,
Issue. 1,
p.
105.
Wu, Chuanxi
1987.
Differential Geometry and Differential Equations.
Vol. 1255,
Issue. ,
p.
160.
Cheng, Qing-Ming
1993.
A characterisation of compact minimal hypersurfaces in a unit sphere.
Bulletin of the Australian Mathematical Society,
Vol. 47,
Issue. 2,
p.
213.
Li, Qichao
2015.
Isometric immersions of generalized Berger spheres in S4(1) and CP2(4).
Journal of Geometry and Physics,
Vol. 98,
Issue. ,
p.
21.

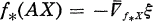 where
where 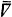 is the covariant differentiation in
is the covariant differentiation in 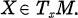 Thus,
Thus, 