Article contents
On Galois groups of class two extensions over the rational number field
Published online by Cambridge University Press: 22 January 2016
Extract
Let Q be the rational number field, K/Q be a maximal Abelian extension whose degree is some power of a prime l, and let f(K) be the conductor of K/Q; if l = 2, let K be complex, and if in addition f(K) ≡ 0 (mod 2), let f(K) ≡ 0 (mod 16). Denote by 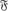 (K) the Geschlechtermodul of K over Q and by K̂ the maximal central l-extension of K/Q contained in the ray class field mod
(K) the Geschlechtermodul of K over Q and by K̂ the maximal central l-extension of K/Q contained in the ray class field mod 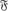 (K) of K. A. Fröhlich [1, Theorem 4] completely determined the Galois group of K̂ over Q in purely rational terms. The proof is based on [1, Theorem 3], though he did not write the proof in the case f(K) ≡ 0 (mod 16). Moreover he gave a classification theory of all class two extensions over Q whose degree is a power of l. Hence we know the set of fields of nilpotency class two over Q, because a finite nilpotent group is a direct product of all its Sylow subgroups. But the theory becomes cumbersome, and it is desirable to reconstruct a more elementary one.
(K) of K. A. Fröhlich [1, Theorem 4] completely determined the Galois group of K̂ over Q in purely rational terms. The proof is based on [1, Theorem 3], though he did not write the proof in the case f(K) ≡ 0 (mod 16). Moreover he gave a classification theory of all class two extensions over Q whose degree is a power of l. Hence we know the set of fields of nilpotency class two over Q, because a finite nilpotent group is a direct product of all its Sylow subgroups. But the theory becomes cumbersome, and it is desirable to reconstruct a more elementary one.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Editorial Board of Nagoya Mathematical Journal 1979
References
- 2
- Cited by

