Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Sagle, Arthur A.
1970.
Some Homogeneous Einstein Manifolds.
Nagoya Mathematical Journal,
Vol. 39,
Issue. ,
p.
81.
Alekseevskii, D. V.
1975.
Lie groups and homogeneous spaces.
Journal of Soviet Mathematics,
Vol. 4,
Issue. 5,
p.
483.
Mikheev, P. O.
and
Sabinin, L. V.
1990.
Smooth quasigroups and geometry.
Journal of Soviet Mathematics,
Vol. 51,
Issue. 6,
p.
2642.
Rodionov, E. D.
1992.
Simply connected compact standard homogeneous Einstein manifolds.
Siberian Mathematical Journal,
Vol. 33,
Issue. 4,
p.
641.
Zusmanovich, Pasha
2010.
ω-Lie algebras.
Journal of Geometry and Physics,
Vol. 60,
Issue. 6-8,
p.
1028.
Goswami, Saikat
Mishra, Satyendra Kumar
and
Mukherjee, Goutam
2024.
Automorphisms of extensions of Lie-Yamaguti algebras and inducibility problem.
Journal of Algebra,
Vol. 641,
Issue. ,
p.
268.

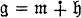 (subspace direct sum) and
(subspace direct sum) and 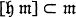 where
where 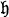 is the Lie algebra of
is the Lie algebra of 