Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Murai, Takafumi
1982.
Lacunary series and ranges of nonsynthesis.
Tohoku Mathematical Journal,
Vol. 34,
Issue. 2,
Murai, Takafumi
1983.
The boundary behaviour of Hadamard lacunary series.
Nagoya Mathematical Journal,
Vol. 89,
Issue. ,
p.
65.
Gnuschke, D.
and
Pommerenke, Ch.
1984.
On annular functions with hadamard gaps.
Complex Variables, Theory and Application: An International Journal,
Vol. 3,
Issue. 1-3,
p.
125.
Berkes, I.
1993.
Critical LIL behavior of the trigonometric system.
Transactions of the American Mathematical Society,
Vol. 338,
Issue. 2,
p.
553.
Kakaroumpas, Spyridon
and
Soler i Gibert, Odí
2024.
Preimages under linear combinations of iterates of finite Blaschke products.
Analysis and Mathematical Physics,
Vol. 14,
Issue. 3,

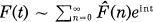 is defined by Spec (
is defined by Spec ( , where
, where 