Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Zhao, Jianqiang
2007.
Analytic continuation of multiple polylogarithms.
Analysis Mathematica,
Vol. 33,
Issue. 4,
p.
301.
Nakamura, Hiroaki
and
Wojtkowiak, Zdzisław
2011.
Non-abelian Fundamental Groups and Iwasawa Theory.
p.
258.
Wojtkowiak, Zdzisław
2012.
The Arithmetic of Fundamental Groups.
p.
339.
Lagarias, Jeffrey C.
and
Li, Wen-Ching Winnie
2016.
The Lerch Zeta function III. Polylogarithms and special values.
Research in the Mathematical Sciences,
Vol. 3,
Issue. 1,
Sakugawa, Kenji
and
Seki, Shin-ichiro
2017.
Finite and étale polylogarithms.
Journal of Number Theory,
Vol. 176,
Issue. ,
p.
279.
Litt, Daniel
2018.
Arithmetic representations of fundamental groups I.
Inventiones mathematicae,
Vol. 214,
Issue. 2,
p.
605.
Hirano, Hikaru
and
Morishita, Masanori
2019.
Arithmetic topology in Ihara theory II: Milnor invariants, dilogarithmic Heisenberg coverings and triple power residue symbols.
Journal of Number Theory,
Vol. 198,
Issue. ,
p.
211.
Nakamura, Hiroaki
and
Wojtkowiak, Zdzisław
2020.
Periods in Quantum Field Theory and Arithmetic.
Vol. 314,
Issue. ,
p.
593.
Nakamura, Hiroaki
and
Shiraishi, Densuke
2025.
Low Dimensional Topology and Number Theory.
Vol. 456,
Issue. ,
p.
237.

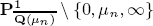 .
.