Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Panchishkin, A. A.
1983.
Modular forms.
Journal of Soviet Mathematics,
Vol. 23,
Issue. 6,
p.
2707.
Guerzhoy, P.
2010.
On a conjecture of Atkin.
Journal für die reine und angewandte Mathematik (Crelles Journal),
Vol. 2010,
Issue. 639,
Urban, Eric
2011.
Eigenvarieties for reductive groups.
Annals of Mathematics,
Vol. 174,
Issue. 3,
p.
1685.
Mahnkopf, Joachim
2017.
Local constancy of dimension of slope subspaces of automorphic forms.
Pacific Journal of Mathematics,
Vol. 289,
Issue. 2,
p.
317.

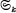 be the space of cusp forms of weight
be the space of cusp forms of weight 