Published online by Cambridge University Press: 22 January 2016
Some functions related to the complex dilogarithmic function
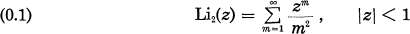
(in the notation of Lewin [9]) are known to occur in connection with algebraic K-theory and characteristic classes (see e.g. Bloch [1], Gelfand-MacPherson [7], Dupont [5], and the references given there). Recently MacPherson and Hain (see [10]) has announced results of a similar kind for some higher polylogarithmic functions. Also Ramakrishnan [11] and [12] has recently studied the classical polylogarithms, which for |z| < 1 are given by

This work is partially supported by grants from Statens Naturvidenskabelige Forskningsråd, Denmark, and the National Science Foundation, U.S.A.