Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Nagase, Haruo
2000.
On a regularity property and a priori estimates for solutions of nonlinear parabolic variational inequalities.
Nagoya Mathematical Journal,
Vol. 160,
Issue. ,
p.
123.

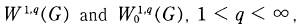 are known. We write the norm of
are known. We write the norm of 