Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Azuhata, Takashi
1984.
On the fundamental units and the class numbers of real quadratic fields.
Nagoya Mathematical Journal,
Vol. 95,
Issue. ,
p.
125.
Mollin, R.A
1986.
Diophantine equations and class numbers.
Journal of Number Theory,
Vol. 24,
Issue. 1,
p.
7.
Lettl, Günter
1986.
A lower bound for the class number of certain cubic number fields.
Mathematics of Computation,
Vol. 46,
Issue. 174,
p.
659.
Hédi, Amara
1986.
Cycles canoniques d’ideaux reduits et nombre des classes de certains corps quadratique reels.
Nagoya Mathematical Journal,
Vol. 103,
Issue. ,
p.
127.
Mollin, R. A.
1987.
Class numbers of quadratic fields determined by solvability of Diophantine equations.
Mathematics of Computation,
Vol. 48,
Issue. 177,
p.
233.
Mollin, R. A.
1987.
On the Insolubility of a Class of Diophantine Equations and the Nontriviality of the Class Numbers of Related Real Quadratic Fields of Richaud-Degert Type.
Nagoya Mathematical Journal,
Vol. 105,
Issue. ,
p.
39.
Sasaki, Ryuji
1988.
Generalized Ono invariant and Rabinovitch’s theorem for real quadratic fields.
Nagoya Mathematical Journal,
Vol. 109,
Issue. ,
p.
117.
Halter-Koch, Franz
1990.
Quadratische ordnungen mit großer Klassenzahl.
Journal of Number Theory,
Vol. 34,
Issue. 1,
p.
82.
Mollin, R. A.
1990.
On the divisor function and class numbers of real quadratic fields, I.
Proceedings of the Japan Academy, Series A, Mathematical Sciences,
Vol. 66,
Issue. 5,
Yokoi, Hideo
1991.
The fundamental unit and bounds for class numbers of real quadratic fields.
Nagoya Mathematical Journal,
Vol. 124,
Issue. ,
p.
181.
Halter-Koch, Franz
1991.
On a class of insoluble binary quadratic diophantine equations.
Nagoya Mathematical Journal,
Vol. 123,
Issue. ,
p.
141.
Hoque, Azizul
and
Saikia, Helen K.
2016.
On the divisibility of class numbers of quadratic fields and the solvability of diophantine equations.
SeMA Journal,
Vol. 73,
Issue. 3,
p.
213.
Hashimoto, Yasufumi
2019.
Asymptotic behaviors of class number sums associated with Pell-type equations.
Mathematische Zeitschrift,
Vol. 292,
Issue. 1-2,
p.
641.


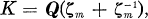 where
where 