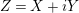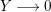ON THE FOURIER COEFFICIENTS OF SIEGEL MODULAR FORMS

Abstract

One can characterize Siegel cusp forms among Siegel modular forms by growth properties of their Fourier coefficients. We give a new proof, which works also for more general types of modular forms. Our main tool is to study the behavior of a modular form for $Z=X+iY$ when $Y\longrightarrow 0$.

1 Introduction and statement of result

Spaces of modular forms usually split up into the direct sum of the subspace generated by Eisenstein series and the subspace of cusp forms, and the Fourier coefficients of the latter, in general, satisfy much better bounds than those of the Eisenstein series. It is natural to ask conversely which bounds one may have to put on the general coefficients of a modular form to guarantee that it is already cuspidal.

This problem has recently attracted a reasonable amount of attention (see, for example, [1–3, 8–10, 12]). Specifically, in the papers [1–3], the case of a Siegel modular form $F$ of integral weight $k$ on a congruence subgroup $\unicode[STIX]{x1D6E4}$ of the Siegel modular group $\unicode[STIX]{x1D6E4}_{n}:=\text{Sp}_{n}(\mathbf{Z})$ of degree $n$ was considered. Recall that if $F$ is cuspidal, then its Fourier coefficients at every cusp of $\unicode[STIX]{x1D6E4}$ are supported on positive definite matrixes $T$ and satisfy the so-called Hecke bound $\ll _{F}(\det T)^{\frac{k}{2}}$ . Conversely, in [2], it was shown that if $k\geqslant 2n$ , and if the coefficients of $F$ at one cusp supported on positive definite $T$ satisfy a bound $\ll _{F}(\det T)^{\unicode[STIX]{x1D6FC}}$ , where $\unicode[STIX]{x1D6FC}<k-n$ , then $F$ already is a cusp form. In particular, if $k>2n$ and those coefficients satisfy the Hecke bound, then $F$ is cuspidal. More generally, including the case of “small weights”, say $k\geqslant \frac{n}{2}+1$ , corresponding statements were proved in [3], for example with the condition $\unicode[STIX]{x1D6FC}<k-n$ relaxed to $\unicode[STIX]{x1D6FC}<k-\frac{n+3}{2}$ , under the additional hypothesis that $\unicode[STIX]{x1D6E4}$ is one of the generalized Hecke congruence subgroups $\unicode[STIX]{x1D6E4}_{n,0}(N)$ of level  $N$ . The tools used in [1–3] were quite deep, including in [1, 2] the theory of $L$ -functions, estimates for Hecke eigenvalues and certain local methods, while in [3], Witt operators and the theory of Fourier–Jacobi expansions were employed.

The purpose of this paper is to contribute a new idea of proof to the above subject, which is simple in the sense that it does not use any deeper structure theorems for the space of modular forms in question. In particular, it is not difficult to see that our arguments can be modified slightly to work also in the case of half-integral weight or for Jacobi forms, Hermitian modular forms or Hilbert–Siegel modular forms. At the same time, we can mildly improve upon or complement the results given in [1–3].

Our proof to a good part is modeled on some arguments given for $n=1$ (i.e. in the case of classical elliptic modular forms) by Miyake [11, pp. 41–42]. They show that an elliptic modular form $f$ of weight $k$ on a subgroup of finite index of $\unicode[STIX]{x1D6E4}_{1}$ is cuspidal, if it satisfies an estimate $f(z)={\mathcal{O}}(y^{-c})$ for $y\rightarrow 0$ , uniformly in $x$ (where $z=x+iy$ , as usual), for some $c<k$ . We show that these arguments can, in fact, be properly modified to work also in the case $n>1$ . Note that from the outset this is not clear at all; for example, for $n>1$ , infinitely many degenerate Fourier coefficients occur and have to be handled appropriately. In the final part of the proof, we also use a “trick” by projecting down a modular form to its Fourier subseries (again modular) supported on indices $T\equiv T_{0}\,(\text{mod}\,p)$ , where $T_{0}$ is a fixed positive definite matrix and $p$ is an odd prime, chosen appropriately. We now state our result in detail.

Theorem.

Let $\unicode[STIX]{x1D6E4}\subset \unicode[STIX]{x1D6E4}_{n}$ be a congruence subgroup, and let $F$ be a Siegel modular form of integral weight $k>n+1$ on $\unicode[STIX]{x1D6E4}$ . Assume that its Fourier coefficients $a(T)$ (where $T$  is a positive definite half-integral matrix of size  $n$ ) at some cusp of $\unicode[STIX]{x1D6E4}$ satisfy the bound

(1) $$\begin{eqnarray}a(T)\ll _{F}(\det T)^{\unicode[STIX]{x1D6FC}},\end{eqnarray}$$

where $\unicode[STIX]{x1D6FC}<k-\frac{n+1}{2}$ . Then, $F$ is a cusp form.

Remarks.

1. (i) It follows from [7, Theorem 1.6.23] that if $k\geqslant 2n+2$ , then the coefficients $a(T)$ (with $T$  positive definite) of any modular form $F$ of weight $k$ on $\unicode[STIX]{x1D6E4}$ satisfy the estimate

   $$\begin{eqnarray}a(T)\ll _{F}(\det T)^{k-\frac{n+1}{2}}.\end{eqnarray}$$
   Thus, in general, the exponent $\unicode[STIX]{x1D6FC}$ in (1) cannot be chosen larger.

2. (ii) If $n=1$ , then the assertion of the Theorem holds with $\unicode[STIX]{x1D6E4}$ replaced by an arbitrary Fuchsian subgroup of $\text{SL}_{2}(\mathbf{R})$ of the first kind (and so, in particular, for a subgroup of $\unicode[STIX]{x1D6E4}_{1}$ of finite index). This follows easily by inspecting the arguments given in [11, pp. 41–42].

3. (iii) We recall that by the well-known “congruence subgroup theorem”, if $n\geqslant 2$ , any subgroup of $\unicode[STIX]{x1D6E4}_{n}$ of finite index already is a congruence subgroup.

The actual proof of the theorem is given in Section 4. In Section 2, we prove some preparatory results needed later, while in Section 3 (proposition), we first give a preliminary version of the theorem. Finally, in Section 5, we comment on some possible generalizations of our results.

Notations. We denote by ${\mathcal{H}}_{n}$ the Siegel upper half-space of degree $n$ , consisting of symmetric complex $(n,n)$ -matrixes with positive imaginary part. If $Z\in {\mathcal{H}}_{n}$ , we write $Z=X+iY$ , with $X=\Re (Z)$ and $Y=\Im (Z)$ . The real symplectic group $\text{Sp}_{n}(\mathbf{R})$ operates on ${\mathcal{H}}_{n}$ by

$$\begin{eqnarray}g\circ Z=(AZ+B)(CZ+D)^{-1}\quad \left(g=\left(\begin{array}{@{}cc@{}}A & B\\ C & D\end{array}\right)\right).\end{eqnarray}$$

If $\unicode[STIX]{x1D6E4}\subset \unicode[STIX]{x1D6E4}_{n}$ is a congruence subgroup, we denote by $M_{k}(\unicode[STIX]{x1D6E4})$ (resp.  $S_{k}(\unicode[STIX]{x1D6E4})$ ) the space of Siegel modular forms (resp. cusp forms) of weight $k\in \mathbf{N}$ with respect to $\unicode[STIX]{x1D6E4}$ . We assume that the reader is familiar with the elementary theory of Siegel modular forms, as for example is contained in [5].

We denote by $E_{n}$ (resp.  $0_{n}$ ) the unit (resp. zero) matrix of size $n$ . For matrixes $A$ and $B$ of appropriate sizes we put as usual $A[B]:=B^{t}AB$ .

If $Y$ is a symmetric real matrix, we write $Y>0$ (resp.  $Y\geqslant 0$ ) if $Y$ is positive definite (resp. positive semi-definite). If $Y>0$ , we denote by $Y^{1/2}$ the (uniquely determined) positive definite matrix whose square is  $Y$ .

If $g\in \text{Sp}_{n}(\mathbf{R})$ , $k\in \mathbf{N}$ , and $F:{\mathcal{H}}_{n}\rightarrow \mathbf{C}$ is a function, we set

$$\begin{eqnarray}(F|_{k}g)(Z):=\det (CZ+D)^{-k}F(g\circ Z)\quad \left(g=\left(\begin{array}{@{}cc@{}}A & B\\ C & D\end{array}\right),Z\in {\mathcal{H}}_{n}\right).\end{eqnarray}$$

2 Some preparatory results

We may assume that $\unicode[STIX]{x1D6E4}=\unicode[STIX]{x1D6E4}_{n}(N)$ is the principal congruence subgroup of level $N$ . If $F\in M_{k}(\unicode[STIX]{x1D6E4})$ , then $F$ at each cusp (say “represented” by $g\in \unicode[STIX]{x1D6E4}\backslash \unicode[STIX]{x1D6E4}_{n}$ ) has a Fourier expansion which has the form

$$\begin{eqnarray}(F|_{k}g)(Z)=\mathop{\sum }_{T\geqslant 0}a_{g}(T)e^{\frac{2\unicode[STIX]{x1D70B}i}{N}tr(TZ)}\quad (Z\in {\mathcal{H}}_{n}).\end{eqnarray}$$

Here, $T$ runs over all positive semi-definite half-integral matrixes of size  $n$ .

In particular, taking $g=E_{2n}$ , we have an expansion “at infinity”

(2) $$\begin{eqnarray}F(Z)=\mathop{\sum }_{T\geqslant 0}a(T)e^{\frac{2\unicode[STIX]{x1D70B}i}{N}tr(TZ)}\quad (Z\in {\mathcal{H}}_{n}).\end{eqnarray}$$

Since $\unicode[STIX]{x1D6E4}\subset \unicode[STIX]{x1D6E4}_{n}$ is a normal subgroup, without loss of generality, to prove the Theorem we may suppose that the estimate (1) holds “at infinity”; that is, for the numbers $a(T)$ in (2). We then have to show that $a_{g}(T)=0$ for all $g\in \unicode[STIX]{x1D6E4}\backslash \unicode[STIX]{x1D6E4}_{n}$ and for all $T\geqslant 0$ that are not positive definite.

The following Lemma will be especially important to our arguments.

Lemma 1. One can choose representatives $g$ in $\unicode[STIX]{x1D6E4}\backslash \unicode[STIX]{x1D6E4}_{n}$ such that $g=\big(\!\begin{smallmatrix}A & B\\ C & D\end{smallmatrix}\!\big)$ , with $\det C\neq 0$ .

Proof. We note that $\unicode[STIX]{x1D6E4}\backslash \unicode[STIX]{x1D6E4}_{n}\simeq \text{Sp}_{n}(\mathbf{Z}/N\mathbf{Z})$ . Choose a prime $p$ not dividing  $N$ . According to the well-known “strong approximation theorem” (one can also argue here in an ad hoc and elementary way), there exists $\tilde{g}\in \unicode[STIX]{x1D6E4}_{n}$ such that

$$\begin{eqnarray}\tilde{g}\equiv g\quad (\text{mod}\,N),\qquad \tilde{g}\equiv \left(\begin{array}{@{}cc@{}}0_{n} & -E_{n}\\ E_{n} & 0_{n}\end{array}\right)\quad (\text{mod}\,p).\end{eqnarray}$$

Then, $\tilde{g}$ and $g$ represent the same class $(\text{mod}\,N)$ , and $\det \tilde{C}\equiv 1\,(\text{mod}\,p)$ (where $\tilde{C}$ denotes the lower left block of $\tilde{g}$ ). This proves the claim.◻

Lemma 2. Suppose that $g=\big(\!\begin{smallmatrix}A & B\\ C & D\end{smallmatrix}\!\big)\in \text{Sp}_{n}(\mathbf{R})$ and $\det C\neq 0$ . Then, for all $Z=X+iY\in {\mathcal{H}}_{n}$ , we have

$$\begin{eqnarray}\Im (g\circ Z)\leqslant Y^{-1}[C^{-1}].\end{eqnarray}$$

Proof. This follows by a direct computation. Indeed, as is well-known,

$$\begin{eqnarray}(\Im (g\circ Z))^{-1}=(CZ+D)Y^{-1}\overline{(CZ+D)}^{t}.\end{eqnarray}$$

Hence, observing that $C$ is invertible and the equation $CD^{t}=DC^{t}$ , we find

$$\begin{eqnarray}\displaystyle (\Im (g\circ Z))^{-1} & = & \displaystyle C(Z+C^{-1}D)Y^{-1}(\overline{Z}+C^{-1}D)C^{t}\nonumber\\ \displaystyle & = & \displaystyle C(iY+R)Y^{-1}(-iY+R)C^{t}\nonumber\\ \displaystyle & = & \displaystyle C(Y+Y^{-1}[R])C^{t},\nonumber\end{eqnarray}$$

where above we have put

$$\begin{eqnarray}R:=X+C^{-1}D.\end{eqnarray}$$

Hence, we obtain

(3) $$\begin{eqnarray}(\Im (g\circ Z))^{-1}\geqslant Y[C^{t}].\end{eqnarray}$$

Taking inverses on both sides of (3), the assertion follows. (Observe that $Y_{1}\geqslant Y_{2}>0$ implies that $Y_{1}^{-1}\leqslant Y_{2}^{-1}$ , as follows by acting with $[Y_{2}^{-1/2}]$ and taking inverses.)

Recall that the series

$$\begin{eqnarray}\mathop{\sum }_{S=S^{t}}(\det (Z+S))^{-\unicode[STIX]{x1D70E}}\quad (Z\in {\mathcal{H}}_{n})\end{eqnarray}$$

(summation over all integral symmetric matrixes of size $n$ ) is absolutely convergent for $\unicode[STIX]{x1D70E}>n$ (cf., e.g., [13, Hilfssatz 38]).◻

Lemma 3. Let $\unicode[STIX]{x1D70E}>n$ and $Y_{0}>0$ . Then, for $Y\leqslant Y_{0}$ , one has

(4) $$\begin{eqnarray}\mathop{\sum }_{S=S^{t}}|\text{det}(iY+S)|^{-\unicode[STIX]{x1D70E}}\ll _{\unicode[STIX]{x1D70E},Y_{0}}(\det Y)^{-\unicode[STIX]{x1D70E}}.\end{eqnarray}$$

Proof. We write the sum on the left-hand side of (4) as

(5) $$\begin{eqnarray}(\det Y)^{-\unicode[STIX]{x1D70E}}\mathop{\sum }_{S=S^{t}}|\text{det}(iE_{n}+S[Y^{-1/2}])|^{-\unicode[STIX]{x1D70E}}.\end{eqnarray}$$

For $Y\leqslant Y_{0}$ , one has

(6) $$\begin{eqnarray}|\text{det}(iE_{n}+S[Y^{-1/2}])|\geqslant |\text{det}(iE_{n}+S[Y_{0}^{-1/2}])|,\end{eqnarray}$$

as will follow from Lemma 4 below, and the expression on the right-hand side of (6) equals

$$\begin{eqnarray}(\det Y_{0})^{-1}|\text{det}(iY_{0}+S)|.\end{eqnarray}$$

Hence, we find that the sum in (5) is bounded from above by

$$\begin{eqnarray}(\det Y_{0})^{\unicode[STIX]{x1D70E}}\mathop{\sum }_{S=S^{t}}|\text{det}(iY_{0}+S)|^{-\unicode[STIX]{x1D70E}},\end{eqnarray}$$

and the latter sum is finite. This proves our assertion.◻

Lemma 4. Let $Y_{0}>0$ . Then, for all symmetric real matrixes $R$ and $Y\leqslant Y_{0}$ , the estimate

(7) $$\begin{eqnarray}|\text{det}(iE_{n}+R[Y^{-1/2}])|\geqslant |\text{det}(iE_{n}+R[Y_{0}^{-1/2}])|\end{eqnarray}$$

holds.

Proof. We first get rid of $Y_{0}$ in (7). For this, we replace $R$ by $R[Y^{1/2}]$ , and then we have to prove that

$$\begin{eqnarray}|\text{det}(iE_{n}+R)|\geqslant |\text{det}(iE_{n}+R[Y^{1/2}][Y_{0}^{-1/2}])|,\end{eqnarray}$$

for all $R=R^{t}$ and $Y\leqslant Y_{0}$ . The right-hand side is equal to

$$\begin{eqnarray}(\det Y_{0})^{-1}|\text{det}(iY_{0}+R[Y^{1/2}])|=(\det Y_{0})^{-1}(\det Y)|\text{det}(iY_{0}[Y^{-1/2}]+R)|.\end{eqnarray}$$

Writing $Y$ for $Y_{0}[Y^{-1/2}]$ , we see that the original condition $Y\leqslant Y_{0}$ becomes $Y\geqslant E_{n}$ and that under the latter condition we have to show that

(8) $$\begin{eqnarray}|\text{det}(iE_{n}+R)|\geqslant (\det Y)^{-1}|\text{det}(iY+R)|.\end{eqnarray}$$

Note that here we can replace $Y$ by $Y[U]$ , where $U$ is orthogonal, and thus we can assume that $Y$ is diagonal. In a final step, we transform the right-hand side of (8) to

$$\begin{eqnarray}|\text{det}(iE_{n}+R[Y^{-1/2}])|,\end{eqnarray}$$

replace $Y^{-1/2}$ by $Y$ and take squares.

Then, we see that we have to prove that

$$\begin{eqnarray}\det (E_{n}+(R[Y])^{2})\leqslant \det (E_{n}+R^{2}),\end{eqnarray}$$

for all $R=R^{t}$ and all diagonal matrixes $Y\leqslant E_{n}$ . We denote the diagonal elements of $Y$ by $y_{1},\ldots ,y_{n}$ .

Since the determinant is linear in columns, for any $(n,n)$ -matrix $C$ we have the equation

$$\begin{eqnarray}\det (E_{n}+C)=\mathop{\sum }_{\unicode[STIX]{x1D708}=0}^{n}\mathop{\sum }_{1\leqslant i_{1}<\cdots <i_{\unicode[STIX]{x1D708}}\leqslant n}\det C_{i_{1}\ldots i_{\unicode[STIX]{x1D708}}},\end{eqnarray}$$

where $C_{i_{1}\ldots i_{\unicode[STIX]{x1D708}}}$ is the $(n,n)$ -matrix that arises from $C$ by replacing the columns with indices $i_{1},\ldots ,i_{\unicode[STIX]{x1D708}}$ by the corresponding standard unit column vectors $e_{i_{1}},\ldots ,e_{i_{\unicode[STIX]{x1D708}}}$ . Note that the cases $\unicode[STIX]{x1D708}=0$ (resp.  $\unicode[STIX]{x1D708}=n$ ) correspond to $\det C$ (resp. 1).

We apply this with $C:=R[Y]^{2}$ . We put $A:=Y^{2}[R]$ . Then, $R[Y]^{2}=A[Y]$ , and we find

$$\begin{eqnarray}\det (E_{n}+R[Y]^{2})=\mathop{\sum }_{\unicode[STIX]{x1D708}=0}^{n}\mathop{\sum }_{1\leqslant i_{1}<\cdots <i_{\unicode[STIX]{x1D708}}\leqslant n}\det A[Y]_{i_{1}\ldots i_{\unicode[STIX]{x1D708}}}.\end{eqnarray}$$

From the Laplace expansion principle, we obtain

$$\begin{eqnarray}\det A[Y]_{i_{1}\ldots i_{\unicode[STIX]{x1D708}}}=\det (y_{i}y_{j}a_{ij})_{\ast },\end{eqnarray}$$

where the lower star in the notation means that double indices $ij$ with $i=i_{1},\ldots ,i_{\unicode[STIX]{x1D708}}$ and any $j$ , or with $j=i_{1},\ldots ,i_{\unicode[STIX]{x1D708}}$ and any $i$ have to be omitted. It follows that

$$\begin{eqnarray}\displaystyle \det (y_{i}y_{j}a_{ij})_{\ast } & = & \displaystyle \left(\mathop{\prod }_{i\neq i_{1},\ldots ,i_{\unicode[STIX]{x1D708}}}y_{i}^{2}\right)\det (a_{ij})_{\ast }\nonumber\\ \displaystyle & {\leqslant} & \displaystyle \det (a_{ij})_{\ast },\nonumber\end{eqnarray}$$

since by assumption $y_{i}\leqslant 1$ for all $i$ . (Note that $A$ , and hence also $(a_{ij})_{\ast }$ , is positive semi-definite.)

We now calculate backwards, that is with $Y$ replaced by $E_{n}$ in $A[Y]$ , and then we see that

$$\begin{eqnarray}\det (E_{n}+R[Y]^{2})\leqslant \det (E_{n}+Y^{2}[R]).\end{eqnarray}$$

However, since $Y^{2}\leqslant E_{n}$ , we have $Y^{2}[R]\leqslant E[R]=R^{2}$ , and therefore we conclude that

$$\begin{eqnarray}\det (E_{n}+R[Y]^{2})\leqslant \det (E_{n}+R^{2}).\end{eqnarray}$$

This proves what we wanted.◻

Remark.

Using the bound $\det (E_{n}+R)\geqslant 1+tr(R)$ , for any $R\geqslant 0$ , one can also estimate the sum in (4) (up to a constant depending only on  $Y_{0}$ ) against the product of $(\det Y)^{-\unicode[STIX]{x1D70E}}$ times the Epstein zeta function of the quadratic form $\mathbf{Z}^{n(n+1)/2}\rightarrow \mathbf{Z},x\mapsto x^{t}x$ in $\frac{n(n+1)}{2}$ variables, evaluated at $\unicode[STIX]{x1D70E}/2$ . However, in this approach, because of convergence reasons, one has to suppose that $\unicode[STIX]{x1D70E}>\frac{n(n+1)}{2}$ (instead of $\unicode[STIX]{x1D70E}>n$ in the above proof). Checking the further arguments, one finds that this leads to the stronger hypothesis $k>\frac{n(n+1)}{2}$ in the theorem.

Lemma 5. Let $R$ be a fixed symmetric real matrix of size $n$ . Then, the following assertions hold.

1. (i) For any $Z=X+iY\in {\mathcal{H}}_{n}$ , one has

   $$\begin{eqnarray}|\text{det}(Z+R)|\geqslant \det Y.\end{eqnarray}$$

2. (ii) For any $Z=X+iY\in {\mathcal{H}}_{n}$ such that $Y\geqslant Y_{0}>0$ and $X$ has bounded components, one has

   $$\begin{eqnarray}|\text{det}(Z+R)|\ll \det Y.\end{eqnarray}$$

Proof.

1. (i) We may incorporate $R$ into $X$ . Then, the assertion is equivalent to saying that

   $$\begin{eqnarray}\det (AA^{t}+E_{n})\geqslant 1,\end{eqnarray}$$
   where $A:=X[Y^{-1/2}]$ . However, this is clear since $AA^{t}\geqslant 0$ .

2. (ii) We proceed in a similar way as in (i). Diagonalizing as usual with orthogonal matrixes, we observe that $Y\geqslant Y_{0}\geqslant cE_{n}$ (where $c>0$ ) implies that the eigenvalues of $Y^{-1}$ (and hence of $Y^{-1/2}$ ) are bounded from above; hence, $Y^{-1/2}$ has bounded components. Hence, under our hypothesis on $X$ , the same is true for $A=X[Y^{-1/2}]$ , and it follows that $\det (AA^{t}+E_{n})\ll 1$ .◻

3 A preliminary version of the theorem

We now prove the theorem first under the additional hypothesis that the Fourier expansion (2) of $F$ is supported on matrixes $T>0$ only. (On the other hand, we need only the slightly weaker assumption $k>n$ here.) More precisely, we have the following.

Proposition.

Assume that $k>n$ . Let $F\in M_{k}(\unicode[STIX]{x1D6E4}_{n}(N))$ , suppose that the Fourier expansion (2) of $F$ is supported on $T>0$ and that

$$\begin{eqnarray}a(T)\ll _{F}(\det T)^{\unicode[STIX]{x1D6FC}},\end{eqnarray}$$

where $\unicode[STIX]{x1D6FC}<k-\frac{n+1}{2}$ . Then, $F$ is in $S_{k}(\unicode[STIX]{x1D6E4}_{n}(N))$ .

Proof. Our assumptions imply that

(9) $$\begin{eqnarray}|F(Z)|\ll _{F}\mathop{\sum }_{T>0}(\det T)^{\unicode[STIX]{x1D6FC}}e^{-\frac{2\unicode[STIX]{x1D70B}}{N}tr(TY)}\quad (Z\in {\mathcal{H}}_{n}).\end{eqnarray}$$

Let us recall the generalized Lipschitz formula (cf., e.g., [13, Hilfssatz 38]), which says that

(10) $$\begin{eqnarray}\mathop{\sum }_{S=S^{t}}(\det (Z+S))^{-\unicode[STIX]{x1D70E}}=C_{n}\frac{e^{-\unicode[STIX]{x1D70B}in\unicode[STIX]{x1D70E}/2}}{\unicode[STIX]{x1D6FE}_{n}(\unicode[STIX]{x1D70E})}\mathop{\sum }_{T>0}(\det T)^{\unicode[STIX]{x1D70E}-\frac{n+1}{2}}e^{2\unicode[STIX]{x1D70B}itr(TZ)}.\end{eqnarray}$$

Here, $Z\in {\mathcal{H}}_{n}$ , $\unicode[STIX]{x1D70E}>n$ and

$$\begin{eqnarray}C_{n}:=(2\sqrt{\unicode[STIX]{x1D70B}})^{-\frac{n(n-1)}{2}},\qquad \unicode[STIX]{x1D6FE}_{n}(\unicode[STIX]{x1D70E}):=(2\unicode[STIX]{x1D70B})^{-n\unicode[STIX]{x1D70E}}\mathop{\prod }_{\unicode[STIX]{x1D708}=0}^{n-1}\unicode[STIX]{x1D6E4}\left(\unicode[STIX]{x1D70E}-\frac{\unicode[STIX]{x1D708}}{2}\right).\end{eqnarray}$$

We apply (10) with $Z=i\frac{1}{N}Y$ and $\unicode[STIX]{x1D70E}=\unicode[STIX]{x1D6FC}+\frac{n+1}{2}$ . Note that we may suppose that $\unicode[STIX]{x1D6FC}>\frac{n-1}{2}$ in (1) (and so $\unicode[STIX]{x1D70E}>n$ ). Indeed, if $\unicode[STIX]{x1D6FC}\leqslant \frac{n-1}{2}$ , then

$$\begin{eqnarray}\unicode[STIX]{x1D6FC}\leqslant \frac{n-1}{2}<k-\frac{n+1}{2}\end{eqnarray}$$

(since $k>n$ by hypothesis), and we may replace $\unicode[STIX]{x1D6FC}$ in (1) by some $\unicode[STIX]{x1D6FC}^{\prime }$ with

$$\begin{eqnarray}\frac{n-1}{2}<\unicode[STIX]{x1D6FC}^{\prime }<k-\frac{n+1}{2},\end{eqnarray}$$

and continue the argument with $\unicode[STIX]{x1D6FC}^{\prime }$ instead of $\unicode[STIX]{x1D6FC}$ .

From (9) and Lemma 3 applied with $\unicode[STIX]{x1D70E}=\unicode[STIX]{x1D6FC}+\frac{n+1}{2}$ , we now find that

(11) $$\begin{eqnarray}|F(Z)|\ll _{Y_{0}}(\det Y)^{-\left(\unicode[STIX]{x1D6FC}+\frac{n+1}{2}\right)}\quad (Z\in {\mathcal{H}}_{n},Y\leqslant Y_{0}),\end{eqnarray}$$

for any fixed $Y_{0}>0$ .

The Fourier coefficients $a_{g}(T)$ have the usual expression,

(12) $$\begin{eqnarray}a_{g}(T)=\int _{X\,(\text{mod}\,E_{n})}F(g\circ Z)\det (CZ+D)^{-k}e^{-\frac{2\unicode[STIX]{x1D70B}i}{N}tr(TZ)}\,dX,\end{eqnarray}$$

valid for any fixed $Y>0$ , where $g=\big(\!\begin{smallmatrix}A & B\\ C & D\end{smallmatrix}\!\big)$ .

By Lemma 1, we may suppose that $C$ is invertible. Then, by Lemma 2, it follows that

$$\begin{eqnarray}\Im (g\circ Z)\leqslant Y^{-1}[C^{-1}].\end{eqnarray}$$

In the following few lines, we always tacitly suppose that $Y\geqslant Y_{0}>0$ .

Given this condition, we deduce that

$$\begin{eqnarray}\Im (g\circ Z)\leqslant Y_{0}^{\ast }:=Y_{0}^{-1}[C^{-1}].\end{eqnarray}$$

Therefore, by (11), we find that

$$\begin{eqnarray}|F(g\circ Z)|\ll _{Y_{0}}(\det \Im (g\circ Z))^{-\left(\unicode[STIX]{x1D6FC}+\frac{n+1}{2}\right)}.\end{eqnarray}$$

Inserting the latter inequality into (12), we obtain

(13) $$\begin{eqnarray}a_{g}(T)\ll _{Y_{0}}\int _{X\,(\text{mod}\,E_{n})}(\det \Im (g\circ Z))^{-(\unicode[STIX]{x1D6FC}+\frac{n+1}{2})}|\text{det}(CZ+D)|^{-k}e^{\frac{2\unicode[STIX]{x1D70B}}{N}tr(TY)}\,dX.\end{eqnarray}$$

From Lemma 5(i) applied with $R=C^{-1}D$ , we find that

(14) $$\begin{eqnarray}|\text{det}(CZ+D)|\gg \det Y.\end{eqnarray}$$

Moreover, under the additional condition that the components of $X$ are bounded, we have

$$\begin{eqnarray}\displaystyle \det \Im (g\circ Z) & = & \displaystyle (\det C)^{-2}(\det Y)|\text{det}(Z+C^{-1}D)|^{-2}\nonumber\\ \displaystyle & \gg & \displaystyle (\det Y)^{-1}\nonumber\end{eqnarray}$$

(where in the last line we use Lemma 5(ii) with $R=C^{-1}D$ ), and hence

(15) $$\begin{eqnarray}(\det \Im (g\circ Z))^{-1}\ll \det Y.\end{eqnarray}$$

Inserting (14) and (15) into (13), we find that

(16) $$\begin{eqnarray}a_{g}(T)\ll _{Y_{0}}(\det Y)^{\unicode[STIX]{x1D6FC}+\frac{n+1}{2}-k}e^{\frac{2\unicode[STIX]{x1D70B}}{N}tr(TY)}.\end{eqnarray}$$

The last inequality holds for any $Y\geqslant Y_{0}>0$ .

Now, let us suppose that $T$ is degenerate. We choose a unimodular matrix $U$ such that

$$\begin{eqnarray}T[U^{t}]=\left(\begin{array}{@{}cc@{}}T_{1} & 0\\ 0 & 0\end{array}\right),\end{eqnarray}$$

with $T_{1}$ of size $0\leqslant r<n$ and $T_{1}$ invertible. Note that

$$\begin{eqnarray}tr(TY)=tr\left(\left(\begin{array}{@{}cc@{}}T_{1} & 0\\ 0 & 0\end{array}\right)Y[U^{-1}]\right),\end{eqnarray}$$

and choose $Y>0$ in such a way that

$$\begin{eqnarray}Y[U^{-1}]=\left(\begin{array}{@{}cc@{}}D_{1} & 0\\ 0 & D_{4}\end{array}\right)\end{eqnarray}$$

is a diagonal matrix with $D_{1}=E_{r}$ and $D_{4}=yE_{n-r}$ , with $y>0$ . Then, clearly,

$$\begin{eqnarray}\displaystyle Y & = & \displaystyle \left(\begin{array}{@{}cc@{}}D_{1} & 0\\ 0 & D_{4}\end{array}\right)[U]\nonumber\\ \displaystyle & {\geqslant} & \displaystyle Y_{0}:=E_{n}[U],\nonumber\end{eqnarray}$$

for $y\geqslant 1$ . Moreover,

$$\begin{eqnarray}tr(TY)=tr(T_{1}D_{1})=tr(T_{1})\end{eqnarray}$$

is constant. Since

$$\begin{eqnarray}\det Y=y^{n-r},\end{eqnarray}$$

letting $y\rightarrow \infty$ we obtain from (16) that $a_{g}(T)=0$ , provided that $\unicode[STIX]{x1D6FC}+\frac{n+1}{2}-k<0$ . Hence, $F$ is cuspidal, as claimed. This proves the proposition.◻

4 Proof of theorem

We now remove the additional hypothesis made in the proposition in Section 3.

If $F$ and $G$ are in $M_{k}(\unicode[STIX]{x1D6E4}_{n}(N))$ , and at least one of them is a cusp form, we denote by

$$\begin{eqnarray}\displaystyle & \displaystyle \langle F,G\rangle =\frac{1}{[\unicode[STIX]{x1D6E4}_{n}:\unicode[STIX]{x1D6E4}_{n}(N)]}\int _{\unicode[STIX]{x1D6E4}_{n}(N)\backslash {\mathcal{H}}_{n}}F(Z)\overline{G(Z)}(\det Y)^{k}\,d\unicode[STIX]{x1D714} & \displaystyle \nonumber\\ \displaystyle & \displaystyle \left(Z=X+iY,dw=\frac{dXdY}{(\det Y)^{n+1}}\right) & \displaystyle \nonumber\end{eqnarray}$$

the normalized Petersson bracket of $F$ and $G$ . Note that the value $\langle F,G\rangle$ is independent of the level of which $F$ and $G$ are considered to be modular, and that $\langle ,\rangle$ defines a scalar product on $S_{k}(\unicode[STIX]{x1D6E4}_{n}(N))$ .

Let

$$\begin{eqnarray}F(Z)=\mathop{\sum }_{T\geqslant 0}a(T)e^{\frac{2\unicode[STIX]{x1D70B}i}{N}tr(TZ)}\quad (Z\in {\mathcal{H}}_{n})\end{eqnarray}$$

be in $M_{k}(\unicode[STIX]{x1D6E4}_{n}(N))$ . Let $T_{0}>0$ , and let $p$ be an odd prime. (The choice of $p$ being odd is only for notational convenience.) Then, we define

(17) $$\begin{eqnarray}F_{T_{0},p}(Z):=\mathop{\sum }_{T\geqslant 0,T\equiv T_{0}\,(\text{mod}\,p)}a(T)e^{\frac{2\unicode[STIX]{x1D70B}i}{N}tr(TZ)}\quad (Z\in {\mathcal{H}}_{n}).\end{eqnarray}$$

Lemma 6.

1. (i) One has $F_{T_{0},p}\in M_{k}(\unicode[STIX]{x1D6E4}_{n}(Np^{2}))$ .

2. (ii) If $\langle F,G\rangle =0$ for all $G\in S_{k}(\unicode[STIX]{x1D6E4}_{n}(N))$ , then $\langle F_{T_{0},p},G\rangle =0$ for all $G\in S_{k}(\unicode[STIX]{x1D6E4}_{n}(Np^{2}))$ .

Proof. This is proved in a standard way. For any symmetric real matrix $S$ , let us put

$$\begin{eqnarray}\unicode[STIX]{x1D6FE}_{n,S}:=\left(\begin{array}{@{}cc@{}}E_{n} & S\\ 0_{n} & E_{n}\end{array}\right).\end{eqnarray}$$

(i) The usual orthogonality relations for roots of unity show that

$$\begin{eqnarray}F_{T_{0},p}(Z)=p^{-\frac{n(n+1)}{2}}\mathop{\sum }_{S=S^{t}\,(\text{mod}\,p)}e^{-2\unicode[STIX]{x1D70B}itr(T_{0}S/p)}F|_{k}\unicode[STIX]{x1D6FE}_{n,NS/p},\end{eqnarray}$$

where the sum extends over all integral symmetric matrixes $S\,(\text{mod}\,p)$ . Since $F$ is modular with respect to $\unicode[STIX]{x1D6E4}_{n}(N)$ , each summand on the right-hand side is modular with respect to $\unicode[STIX]{x1D6E4}_{n}(Np^{2})$ , as is easily checked. Hence, we deduce that $F_{T_{0},p}$ is in $M_{k}(\unicode[STIX]{x1D6E4}_{n}(Np^{2}))$ .

(ii) Let $G\in S_{k}(\unicode[STIX]{x1D6E4}_{n}(Np^{2}))$ . Then, the usual formalism of the Petersson bracket shows that

$$\begin{eqnarray}\displaystyle p^{\frac{n(n+1)}{2}}\langle F_{T_{0},p},G\rangle & = & \displaystyle \mathop{\sum }_{S=S^{t}\,(\text{mod}\,p)}e^{-2\unicode[STIX]{x1D70B}itr(T_{0}S/p)}\langle F|_{k}\unicode[STIX]{x1D6FE}_{n,NS/p},G\rangle \nonumber\\ \displaystyle & = & \displaystyle \mathop{\sum }_{S=S^{t}\,(\text{mod}\,p)}e^{-2\unicode[STIX]{x1D70B}itr(T_{0}S/p)}\langle F,G|_{k}\unicode[STIX]{x1D6FE}_{n,-NS/p}\rangle .\nonumber\end{eqnarray}$$

Note that $G|_{k}\unicode[STIX]{x1D6FE}_{n,-NS/p}$ is modular with respect to $\unicode[STIX]{x1D6E4}_{n}(Np^{4})$ (cf. (i)). Thus, we obtain

(18) $$\begin{eqnarray}\displaystyle \qquad p^{\frac{n(n+1)}{2}}\langle F_{T_{0},p},G\rangle =\mathop{\sum }_{S=S^{t}\,(\text{mod}\,p)}e^{-2\unicode[STIX]{x1D70B}itr(T_{0}S/p)}\langle F,tr_{Np^{4}}^{N}(G|_{k}\unicode[STIX]{x1D6FE}_{n,-NS/p})\rangle , & & \displaystyle\end{eqnarray}$$

where

$$\begin{eqnarray}\displaystyle & \displaystyle tr_{Np^{4}}^{N}:M_{k}(\unicode[STIX]{x1D6E4}_{n}(Np^{4}))\rightarrow M_{k}(\unicode[STIX]{x1D6E4}_{n}(N)), & \displaystyle \nonumber\\ \displaystyle & \displaystyle H\mapsto \frac{1}{[\unicode[STIX]{x1D6E4}_{n}(N):\unicode[STIX]{x1D6E4}_{n}(Np^{4})]}\mathop{\sum }_{L\in \unicode[STIX]{x1D6E4}_{n}(Np^{4})\backslash \unicode[STIX]{x1D6E4}_{n}(N)}H|_{k}L & \displaystyle \nonumber\end{eqnarray}$$

is the usual trace map (adjoint to the inclusion map on subspaces of cusp forms). Since with $H$ also $tr_{Np^{4}}^{N}(H)$ is cuspidal, our hypothesis implies that the right-hand side of (18) is zero, as was to be shown.

We now prove the Theorem. By elementary linear algebra, there is a decomposition

(19) $$\begin{eqnarray}M_{k}(\unicode[STIX]{x1D6E4}_{n}(N))=C_{k}(\unicode[STIX]{x1D6E4}_{n}(N))\oplus S_{k}(\unicode[STIX]{x1D6E4}_{n}(N)),\end{eqnarray}$$

where

$$\begin{eqnarray}C_{k}(\unicode[STIX]{x1D6E4}_{n}(N)):=\{F\in M_{k}(\unicode[STIX]{x1D6E4}_{n}(N))|\langle F,G\rangle =0\,\forall G\in S_{k}(\unicode[STIX]{x1D6E4}_{n}(N))\}.\end{eqnarray}$$

Let $F\in M_{k}(\unicode[STIX]{x1D6E4}_{n}(N))$ , and suppose that (1) holds. We may assume that $\frac{k}{2}\leqslant \unicode[STIX]{x1D6FC}$ . Otherwise, $\unicode[STIX]{x1D6FC}<\frac{k}{2}$ , and then the bound (1) would imply that also $a(T)\ll (\det T)^{k/2}$ , and we can finish the argument with $\unicode[STIX]{x1D6FC}$ replaced by $\unicode[STIX]{x1D6FC}^{\prime }=\frac{k}{2}$ . Note that $\frac{k}{2}<k-\frac{n+1}{2}$ since $k>n+1$ by hypothesis.

We write $F=F_{1}+F_{2}$ , with $F_{1}\in C_{k}(\unicode[STIX]{x1D6E4}_{n}(N))$ and $F_{2}\in S_{k}(\unicode[STIX]{x1D6E4}_{n}(N))$ according to (19). By the assumption $\frac{k}{2}\leqslant \unicode[STIX]{x1D6FC}$ , and since the Fourier coefficients of cusp forms satisfy the bound $\ll (\det T)^{k/2}$ , the $T$ th Fourier coefficients $b(T)\,(T>0)$ of $F_{1}=F-F_{2}$ satisfy (1). Suppose that there exists $T_{0}>0$ with $b(T_{0})\neq 0$ . Let $p$ be an odd prime not dividing $\det (2T_{0})$ . Then, the function $(F_{1})_{T_{0},p}$ defined by (17) is in $M_{k}(\unicode[STIX]{x1D6E4}_{n}(Np^{2}))$ , by Lemma 6(i), and has Fourier coefficients supported on positive definite matrixes which again satisfy (1) by definition (17). Therefore, by the proposition, $(F_{1})_{T_{0},p}$ is a cusp form. At the same time, by Lemma 6(ii),

$$\begin{eqnarray}\langle (F_{1})_{T_{0},p},G\rangle =0,\end{eqnarray}$$

for all $G\in S_{k}(\unicode[STIX]{x1D6E4}_{n}(Np^{2}))$ . Hence, we conclude that $(F_{1})_{T_{0},p}=0$ . In particular, $b(T_{0})=0$ , a contradiction. Therefore, the Fourier expansion of $F_{1}$ is supported on degenerate matrixes; that is, $F_{1}$ is a singular modular form and we necessarily must have $k<\frac{n}{2}$ unless $F_{1}=0$ (see, for example, [5]). However, $k>n+1$ by assumption, and so we finally conclude that $F=F_{2}$ is cuspidal.

This proves the theorem.◻

5 Generalizations

Our method seems to be rather robust and very flexible. We essentially only need growth properties of the modular form $F(Z)$ in question when $\det Y\rightarrow 0$ (in an appropriate way). These, in turn, rely on the generalized Lipschitz formula. In particular, essentially no arithmetic is involved, and therefore issues like class numbers should play no role in generalizations. We now briefly comment on cases of interest.

(i) Nonintegral weights. There should be no problem at all for nonintegral weights (including not only the half-integral weight case, but also more general rational weights for the group $GL(2)$ ).

(ii) Orthogonal modular forms. Modular forms on $\text{SO}(2,n)$ can be treated in a similar was as here. Note that $\text{SO}(2,3)$ is isogenous to $\text{Sp}(2)$ .

(iii) Jacobi forms. There is no real new issue here, also for Jacobi forms of higher degree. (For the basic theory we refer to [4, 14].) One uses theta expansions and observes that the coefficients in these theta expansions give vectors of modular forms associated with a (projective) representation of finite co-kernel. In other words, we consider ordinary (Siegel) modular forms of lower degree, lower (possibly half-integral) weight and higher level. We note that the case of classical Jacobi forms was first treated in [9], using quite a different method.

(iv) Hermitian modular forms. The only new point here is the class number of the imaginary quadratic field in question. We just point out that in Section 4 it is not really necessary to use an integral matrix to transform a (symmetric or Hermitian) matrix into the form $\big(\!\begin{smallmatrix}\ast & 0\\ 0 & 0\end{smallmatrix}\!\big)$ ; one can do this as well with a matrix whose coefficients are in the field in question.

(v) Hilbert (–Siegel) modular forms. Our setting allows a straightforward application to the Hilbert modular case. It suffices to look at imaginary parts of type $(y,\ldots ,y)\in \mathbf{R}_{+}^{n}$ in the variables of such a form and let $y\rightarrow 0$ . Here, $n$ is the degree of the totally real number field in question. An extension to Hilbert–Siegel modular forms is also immediate. We mention that the case of Hilbert modular forms (using different techniques) in an adelic setting was previously treated in [10].

(vi) Vector-valued modular forms. For a finite dimensional complex vector space $V$ and a polynomial representation $\unicode[STIX]{x1D70C}:GL(n,\mathbf{C})\rightarrow GL(V)$ , one can consider $V$ -valued Siegel modular forms with respect to the automorphy factor $\unicode[STIX]{x1D70C}$ . The Hecke bound for cusp forms $F$ can then be stated as

$$\begin{eqnarray}\Vert \unicode[STIX]{x1D70C}(T^{-1/2})a_{F}(T)\Vert \leqslant C\quad (T>0)\end{eqnarray}$$

for some constant $C>0$ (see [6]), where $\Vert \,\Vert$ is the norm on $V$ which comes from a scalar product on $V$ , such that the group $U(n,\mathbf{C})$ acts unitarily and $(a_{F}(T))\in V$ is the vector of Fourier coefficients of $F$ . We may decompose $\unicode[STIX]{x1D70C}$ as $\unicode[STIX]{x1D70C}_{0}\otimes \det ^{k}$ with the largest positive integer $k$ such that $\unicode[STIX]{x1D70C}_{0}$ is still a polynomial representation. Then, we may call $k$ the weight of $\unicode[STIX]{x1D70C}$ . The estimate above then reads

$$\begin{eqnarray}\Vert \unicode[STIX]{x1D70C}_{0}(T^{-1/2})a_{F}(T)\Vert \leqslant C\det (T)^{k/2}.\end{eqnarray}$$

It is not immediately clear how to deduce from this an estimate for the behavior of $F$ when $\det Y$ goes to zero, information that seems to be necessary to get started at all with our approach. Moreover, an appropriate substitute for the Lipschitz formula seems to be missing.

Note, however, that the approach via Hecke operators chosen in [2] leads to some positive results in this setting.