Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Lawrence, John
and
Zorzitto, Frank
1978.
Counting eigenvalues for automorphisms of Riemann surfaces.
Proceedings of the American Mathematical Society,
Vol. 69,
Issue. 1,
p.
91.
Duma, Andrei
1982.
Die 3-Weierstrass-Punkte �ber dem Teichm�ller-Raum T2.
Manuscripta Mathematica,
Vol. 38,
Issue. 2,
p.
201.

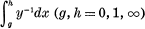 are solutions of the Gauss’s differential equation
are solutions of the Gauss’s differential equation