Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Accardi, Luigi
and
Bożejko, Marek
1998.
Interacting Fock Spaces and Gaussianization of Probability Measures.
Infinite Dimensional Analysis, Quantum Probability and Related Topics,
Vol. 01,
Issue. 04,
p.
663.
ASAI, NOBUHIRO
2001.
ANALYTIC CHARACTERIZATION OF ONE-MODE INTERACTING FOCK SPACE.
Infinite Dimensional Analysis, Quantum Probability and Related Topics,
Vol. 04,
Issue. 03,
p.
409.
ACCARDI, L.
CRISMALE, V.
and
LU, Y. G.
2005.
CONSTRUCTIVE UNIVERSAL CENTRAL LIMIT THEOREMS BASED ON INTERACTING FOCK SPACES.
Infinite Dimensional Analysis, Quantum Probability and Related Topics,
Vol. 08,
Issue. 04,
p.
631.
LENCZEWSKI, ROMUALD
and
SAŁAPATA, RAFAŁ
2006.
DISCRETE INTERPOLATION BETWEEN MONOTONE PROBABILITY AND FREE PROBABILITY.
Infinite Dimensional Analysis, Quantum Probability and Related Topics,
Vol. 09,
Issue. 01,
p.
77.
ACCARDI, LUIGI
LENCZEWSKI, ROMUALD
and
SAŁAPATA, RAFAŁ
2007.
DECOMPOSITIONS OF THE FREE PRODUCT OF GRAPHS.
Infinite Dimensional Analysis, Quantum Probability and Related Topics,
Vol. 10,
Issue. 03,
p.
303.
CRISMALE, VITONOFRIO
and
LU, YUN GANG
2007.
ROTATION INVARIANT INTERACTING FOCK SPACES.
Infinite Dimensional Analysis, Quantum Probability and Related Topics,
Vol. 10,
Issue. 02,
p.
211.
LENCZEWSKI, ROMUALD
and
SAŁAPATA, RAFAŁ
2008.
NONCOMMUTATIVE BROWNIAN MOTIONS ASSOCIATED WITH KESTEN DISTRIBUTIONS AND RELATED POISSON PROCESSES.
Infinite Dimensional Analysis, Quantum Probability and Related Topics,
Vol. 11,
Issue. 03,
p.
351.
Kang, Yuanbao
and
Wang, Caishi
2015.
Quantum Stochastic Integral Representations on Interacting Fock Space.
Journal of Theoretical Probability,
Vol. 28,
Issue. 3,
p.
1007.
Crismale, Vitonofrio
Fidaleo, Francesco
and
Lu, Yun Gang
2017.
From discrete to continuous monotone C*-algebras via quantum central limit theorems.
Infinite Dimensional Analysis, Quantum Probability and Related Topics,
Vol. 20,
Issue. 02,
p.
1750013.
Wang, Caishi
Wang, Ce
Tang, Yuling
and
Ren, Suling
2018.
Quantum Walk in Terms of Quantum Bernoulli Noise and Quantum Central Limit Theorem for Quantum Bernoulli Noise.
Advances in Mathematical Physics,
Vol. 2018,
Issue. ,
p.
1.
Accardi, Luigi
and
Lu, Yun-Gang
2018.
The qq-bit (I): Central limits with left q-Jordan–Wigner embeddings, monotone interacting Fock space, Azema random variable, probabilistic meaning of q.
Infinite Dimensional Analysis, Quantum Probability and Related Topics,
Vol. 21,
Issue. 04,
p.
1850030.
Lu, Yungang
2024.
Probabilistic analysis of the (
q
, 2)-Fock space: vacuum distribution and moments of the field operator
.
Stochastics,
Vol. 96,
Issue. 8,
p.
2110.


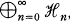 , where,
, where, 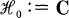 is the complex field and
is the complex field and 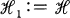 is a given Hilbert space.
is a given Hilbert space.