Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Kuz'min, L. V.
1987.
Algebraic number fields.
Journal of Soviet Mathematics,
Vol. 38,
Issue. 3,
p.
1930.
Bondarko, M. V.
2002.
Idempotents in the Endomorphism Ring of an Ideal in a p-Extension of a Complete, Discrete Valuation Field with Residue Field of Characteristic p as a Galois Module.
Journal of Mathematical Sciences,
Vol. 112,
Issue. 3,
p.
4255.

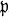 -adic number field
-adic number field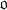 be the ring of all integers in
be the ring of all integers in 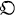 of all integers in
of all integers in 