Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Watanabe, Toshiro
1992.
Sufficient conditions for unimodality of nonsymmetric Lévy processes.
Kodai Mathematical Journal,
Vol. 15,
Issue. 1,
Watanabe, Toshiro
1993.
Oscillation of modes of some semi-stable Lévy processes.
Nagoya Mathematical Journal,
Vol. 132,
Issue. ,
p.
141.
WATANABE, Toshiro
1999.
On Bessel transforms of multimodal increasing Lévy processes.
Japanese journal of mathematics. New series,
Vol. 25,
Issue. 2,
p.
227.
Hanyga, Andrzej
2002.
Multi–dimensional solutions of space–time–fractional diffusion equations.
Proceedings of the Royal Society of London. Series A: Mathematical, Physical and Engineering Sciences,
Vol. 458,
Issue. 2018,
p.
429.
Cuvillier, Philippe
and
Cont, Arshia
2014.
Coherent time modeling of Semi-Markov models with application to real-time audio-to-score alignment.
p.
1.

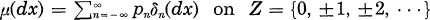 is said to be unimodal with mode
is said to be unimodal with mode 