Article contents
On the structure of local cohomology modules for monomial curves in 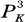
Published online by Cambridge University Press: 22 January 2016
Extract
Our setting for this paper is projective 3-space 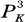 over an algebraically closed field K. By a curve C ⊂
over an algebraically closed field K. By a curve C ⊂ 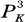 is meant a 1-dimensional, equidimensional projective algebraic set, which is locally Cohen-Macaulay. Let
is meant a 1-dimensional, equidimensional projective algebraic set, which is locally Cohen-Macaulay. Let 
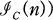 be the Hartshorne-Rao module of finite length (cf. [R]). Here Z is the set of integers and ℐc the ideal sheaf of C. In [GMV] it is shown that
be the Hartshorne-Rao module of finite length (cf. [R]). Here Z is the set of integers and ℐc the ideal sheaf of C. In [GMV] it is shown that  , where
, where  is the homogeneous ideal of C,
is the homogeneous ideal of C,  is the first local cohomology module of the R-module M with respect to
is the first local cohomology module of the R-module M with respect to 
 , (see also the discussion on the 1-st local cohomology module in [GW]). Also in [GMV] it is shown that k = 0 if and only if C is arithmetically Cohen-Macaulay and C is arithmetically Buchsbaum if and only if k ≤ 1. We therefore have the following natural definition.
, (see also the discussion on the 1-st local cohomology module in [GW]). Also in [GMV] it is shown that k = 0 if and only if C is arithmetically Cohen-Macaulay and C is arithmetically Buchsbaum if and only if k ≤ 1. We therefore have the following natural definition.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Editorial Board of Nagoya Mathematical Journal 1994
References
 , Math. Nachr., 96 (1980), 257–269.Google Scholar
, Math. Nachr., 96 (1980), 257–269.Google Scholar- 8
- Cited by

