Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Ishii, Tadashi
1955.
On semi-reducible measures.
Proceedings of the Japan Academy, Series A, Mathematical Sciences,
Vol. 31,
Issue. 10,
Hodel, Richard E.
1966.
Total normality and the hereditary property.
Proceedings of the American Mathematical Society,
Vol. 17,
Issue. 2,
p.
462.
Greever, John
1968.
On screenable topological spaces.
Proceedings of the Japan Academy, Series A, Mathematical Sciences,
Vol. 44,
Issue. 6,
Sakai, Masao
1970.
On a theorem of E. Michael and K. Nagami.
Proceedings of the Japan Academy, Series A, Mathematical Sciences,
Vol. 46,
Issue. 6,
1970.
Vol. 37,
Issue. ,
p.
245.
Aull, C. E.
1971.
Topological spaces with a 𝜎-point finite base.
Proceedings of the American Mathematical Society,
Vol. 29,
Issue. 2,
p.
411.
Ishii, Tadashi
and
Shiraki, Takanori
1971.
Some properties of $wM$-spaces.
Proceedings of the Japan Academy, Series A, Mathematical Sciences,
Vol. 47,
Issue. 2,
Steen, L. A.
1972.
Conjectures and Counterexamples in Metrization Theory.
The American Mathematical Monthly,
Vol. 79,
Issue. 2,
p.
113.
Boone, James R.
1973.
A characterization of metacompactness in the class of θ-refinable spaces.
General Topology and its Applications,
Vol. 3,
Issue. 3,
p.
253.
Katuta, Yûkiti
1974.
On spaces which admit closure-preserving covers by compact sets.
Proceedings of the Japan Academy, Series A, Mathematical Sciences,
Vol. 50,
Issue. 10,
Kramer, Thomas R.
1976.
On the product of two topological spaces.
General Topology and its Applications,
Vol. 6,
Issue. 1,
p.
1.
Lewis, I.W.
1977.
On covering properties of subspaces of R.H. Bing's example G.
General Topology and its Applications,
Vol. 7,
Issue. 1,
p.
109.
Junnila, Heikki J.K.
1980.
Surveys in General Topology.
p.
195.
Hung, H. H.
1981.
A refinement on Michael’s characterization of paracompactness.
Proceedings of the American Mathematical Society,
Vol. 83,
Issue. 1,
p.
179.
Palenz, Diana G.P.
1982.
Monotone normality and paracompactness.
Topology and its Applications,
Vol. 14,
Issue. 2,
p.
171.
Rudin, Mary Ellen
1983.
A normal screenable non-paracompact space.
Topology and its Applications,
Vol. 15,
Issue. 3,
p.
313.
Rudin, Mary Ellen
1983.
Collectionwise normality in screenable spaces.
Proceedings of the American Mathematical Society,
Vol. 87,
Issue. 2,
p.
347.
RUDIN, Mary Ellen
1984.
Handbook of Set-Theoretic Topology.
p.
761.
BURKE, Dennis K.
1984.
Handbook of Set-Theoretic Topology.
p.
347.
Collins, P. J.
Reed, G. M.
Roscoe, A. W.
and
Rudin, M. E.
1985.
A lattice of conditions on topological spaces.
Proceedings of the American Mathematical Society,
Vol. 94,
Issue. 3,
p.
487.

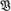 of it has a
of it has a 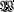 , that is, an open covering for which the stars (
, that is, an open covering for which the stars (