Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Naitoh, Hiroo
1983.
Parallel submanifolds of complex space forms II.
Nagoya Mathematical Journal,
Vol. 91,
Issue. ,
p.
119.
Blomstrom, Carol
1985.
Global Differential Geometry and Global Analysis 1984.
Vol. 1156,
Issue. ,
p.
30.
Reckziegel, Helmut
1985.
Global Differential Geometry and Global Analysis 1984.
Vol. 1156,
Issue. ,
p.
264.
Tsukada, Kazumi
1985.
Parallel Kaehler submanifolds of Hermitian symmetric spaces.
Mathematische Zeitschrift,
Vol. 190,
Issue. 1,
p.
129.
Ohnita, Yoshihiro
1986.
Totally real submanifolds with nonnegative sectional curvature.
Proceedings of the American Mathematical Society,
Vol. 97,
Issue. 3,
p.
474.
Urbano, Francisco
1986.
Nonnegatively curved totally real submanifolds.
Mathematische Annalen,
Vol. 273,
Issue. 2,
p.
345.
Funabashi, Shōichi
1986.
Automorphisms and a reduction theorem in a Sasakian space form E2m+1(−3).
Annali di Matematica Pura ed Applicata,
Vol. 145,
Issue. 1,
p.
317.
Dajczer, Marcos
and
Thorbergsson, Gudlaugur
1987.
Holomorphicity of minimal submanifolds in complex space forms.
Mathematische Annalen,
Vol. 277,
Issue. 3,
p.
353.
Li, An -Min
and
Zhao, Guosong
1994.
Totally real minimal submanifolds inC P n.
Archiv der Mathematik,
Vol. 62,
Issue. 6,
p.
562.
Baikoussis, Christos
Blair, David E.
and
Koufogiorgos, Themis
1995.
Integral submanifolds of sasakian space forms % MathType!MTEF!2!1!+-% feaaeaart1ev0aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn% hiov2DGi1BTfMBaeXanrfitLxBI9gBaerbd9wDYLwzYbItLDharqqt% ubsr4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq% -Jc9vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0x% fr-xfr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamyuam% aaBaaaleaacaaIXaGaaGimaaqabaGccqGH9aqpciGGSbGaaiOBaiaa% ysW7caWGRbWaaSbaaSqaaiaadsfacaaIXaaabeaakiaac+cacaWGRb% WaaSbaaSqaaiaadsfacaaIYaaabeaakiabg2da9iabgkHiTmaabmaa% baGaamyramaaBaaaleaacaWGHbaabeaakiaac+cacaWGsbaacaGLOa% GaayzkaaGaey41aq7aaiWaaeaadaqadaqaaiaadsfadaWgaaWcbaGa% aGOmaaqabaGccqGHsislcaWGubWaaSbaaSqaaiaaigdaaeqaaaGcca% GLOaGaayzkaaGaai4laiaacIcacaWGubWaaSbaaSqaaiaaikdaaeqa% aOGaaGjbVlaadsfadaWgaaWcbaGaamysaaqabaGccaGGPaaacaGL7b% GaayzFaaaaaa!5C4A! $ {\bar M}^{7}(k) $.
Results in Mathematics,
Vol. 27,
Issue. 3-4,
p.
207.
González-Dávila, J. C.
and
Vanhecke, L.
1999.
Locally symmetric immersions.
Czechoslovak Mathematical Journal,
Vol. 49,
Issue. 3,
p.
491.
2000.
Vol. 1,
Issue. ,
p.
187.
Castro, Ildefonso
and
Vrancken, Luc
2001.
Minimal Lagrangian submanifolds in ℂP 3 and the sinh-Gordon equation.
Results in Mathematics,
Vol. 40,
Issue. 1-4,
p.
130.
Amarzaya, Amartuvshin
and
Ohnita, Yoshihiro
2003.
Hamiltonian stability of certain minimal Lagrangian submanifolds in complex projective spaces.
Tohoku Mathematical Journal,
Vol. 55,
Issue. 4,
Li, Haizhong
and
Vrancken, Luc
2005.
A basic inequality and new characterization of Whitney spheres in a complex space form.
Israel Journal of Mathematics,
Vol. 146,
Issue. 1,
p.
223.
Alekseevsky, Dmitri V.
Di Scala, Antonio J.
and
Marchiafava, Stefano
2005.
Parallel Kähler submanifolds of quaternionic Kähler symmetric spaces.
Tohoku Mathematical Journal,
Vol. 57,
Issue. 4,
Chen, Bang-Yen
and
Van der Veken, Joeri
2009.
Complete classification of parallel surfaces in 4-dimensional Lorentzian space forms.
Tohoku Mathematical Journal,
Vol. 61,
Issue. 1,
Ma, Hui
and
Ohnita, Yoshihiro
2009.
On Lagrangian submanifolds in complex hyperquadrics and isoparametric hypersurfaces in spheres.
Mathematische Zeitschrift,
Vol. 261,
Issue. 4,
p.
749.
Jentsch, Tillmann
2010.
The extrinsic holonomy Lie algebra of a parallel submanifold.
Annals of Global Analysis and Geometry,
Vol. 38,
Issue. 4,
p.
335.
CHEN, BANG-YEN
DILLEN, FRANKI
and
VAN DER VEKEN, JOERI
2010.
COMPLETE CLASSIFICATION OF PARALLEL LORENTZIAN SURFACES IN LORENTZIAN COMPLEX SPACE FORMS.
International Journal of Mathematics,
Vol. 21,
Issue. 05,
p.
665.

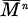 (
(