Hostname: page-component-745bb68f8f-grxwn Total loading time: 0 Render date: 2025-01-16T02:00:22.507Z Has data issue: false hasContentIssue false
  • English
  • Français

PRESENTING INFINITESIMAL q-SCHUR ALGEBRAS

Part of: Lie algebras and Lie superalgebras Linear algebraic groups and related topics

Published online by Cambridge University Press:  13 January 2025

QIANG FU Open the ORCID record for QIANG FU [Opens in a new window]  and
CHENGQUAN SUN Open the ORCID record for CHENGQUAN SUN [Opens in a new window]
QIANG FU*
Affiliation:
School of Mathematical Sciences, Key Laboratory of Intelligent Computing and Applications (Ministry of Education) Tongji University Shanghai, 200092 China
CHENGQUAN SUN
Affiliation:
School of Mathematical Sciences Tongji University Shanghai, 200092 China suncq131@163.com
*
q.fu@tongji.edu.cn q.fu@hotmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

Let be a commutative ring containing a primitive 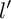$l'$th root 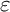$\varepsilon $ of 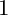$1$. The infinitesimal q-Schur algebras over form an ascending chain of subalgebras of the q-Schur algebra , which are useful in studying representations of the Frobenius kernel of the associated quantum linear group. Let be the quantized enveloping algebra of 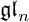$\mathfrak {gl}_n$ over . There is a natural surjective algebra homomorphism 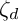$\zeta _{d}$ from to . 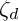The map $\zeta _{d}$ restricts to a surjective algebra homomorphism 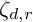$\zeta _{d,r}$ from to , where is a certain Hopf subalgebra of , which is closely related to Frobenius–Lusztig kernels of . We give the extra defining relations needed to define the infinitesimal q-Schur algebra as a quotient of . 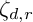The map $\zeta _{d,r}$ induces a surjective algebra homomorphism , where is the modified quantum algebra associated with . We also give a generating set for the kernel of 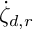$\dot {\zeta }_{d,r}$. These results can be used to give a classification of irreducible -modules over a field of characteristic p.

Keywords

infinitesimal q-Schur algebraFrobenius–Lusztig kernelsthe quantized enveloping algebra of gln

MSC classification

Primary: 20G43: Schur and $q$-Schur algebras 17B37: Quantum groups (quantized enveloping algebras) and related deformations
Type
Article
Information
Nagoya Mathematical Journal , First View , pp. 1 - 22
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of Foundation Nagoya Mathematical Journal

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Andersen, H., Polo, P. and Wen, K., Representations of quantum algebras , Invent. Math. 104 (1991), 1–59.CrossRefGoogle Scholar
Andersen, H., Polo, P. and Wen, K., Injective modules for quantum algebras , Amer. J. Math. 114 (1992), 571–604.CrossRefGoogle Scholar
Beilinson, A. A., Lusztig, G. and MacPherson, R., A geometric setting for the quantum deformation of $G{L}_n$ , Duke Math. J. 61 (1990), 655–677.CrossRefGoogle Scholar
Cox, A. G., On some applications of infinitesimal methods to quantum groups and related algebras, Ph.D. thesis, University of London, 1997.Google Scholar
Cox, A. G., On the blocks of the infinitesimal Schur algebras , Q. J. Math. 51 (2000), 39–56.CrossRefGoogle Scholar
Dipper, R. and James, G., $q$ -Tensor spaces and $q$ -Weyl modules , Trans. Amer. Math. Soc. 327 (1991), 251–282.Google Scholar
Doty, S., Presenting generalized $q$ -Schur algebras , Represent. Theory 7 (2003), 196–213.CrossRefGoogle Scholar
Doty, S. and Giaquinto, A., Presenting Schur algebras , Int. Math. Res. Not. IMRN 36 (2002), 1907–1944.CrossRefGoogle Scholar
Doty, S., Giaquinto, A. and Sullivan, J., Presenting generalized Schur algebras in types $B,C,D$ , Adv. Math. 206 (2006), 434–454.CrossRefGoogle Scholar
Doty, S., Giaquinto, A. and Sullivan, J., On the defining relations for generalized $q$ -Schur algebras , Adv. Math. 221 (2009), 955–982.CrossRefGoogle Scholar
Doty, S. R., Nakano, D. K. and Peters, K.M., On infinitesimal Schur algebras , Proc. Lond. Math. Soc. s3-72 (1996), 588–612.CrossRefGoogle Scholar
Drupieski, C. M., Representations and cohomology for Frobenius–Lusztig kernels , J. Pure Appl. Algebra 215 (2011), 1473–1491.CrossRefGoogle Scholar
Du, J., A note on the quantized Weyl reciprocity at roots of unity , Algebra Colloq. 2 (1995), 363–372.Google Scholar
Du, J. and Fu, Q., Quantum ${\mathfrak{gl}}_{\infty }$ , infinite $q$ -Schur algebras and their representations , J. Algebra 322 (2009), 1516–1547.CrossRefGoogle Scholar
Du, J. and Parshall, B., Monomial bases for $q$ -Schur algebras , Trans. Amer. Math. Soc. 355 (2003), 1593–1620.CrossRefGoogle Scholar
Fu, Q., A comparison of infinitesimal and little $q$ -Schur algebras, Comm. Algebra 33 (2005), 2663–2682.CrossRefGoogle Scholar
Fu, Q., Canonical bases for modified quantum ${\mathfrak{gl}}_n$ and $q$ -Schur algebras, J. Algebra 406 (2014), 308–320.CrossRefGoogle Scholar
Fu, Q., BLM realization for Frobenius–Lusztig Kernels of type $A$ , Math. Res. Lett. 23 (2016), 1329–1350.CrossRefGoogle Scholar
Fu, Q. and Gao, W., Presenting integral $q$ -Schur algebras , Internat. J. Math. 30 (2019), 1950002, 14 pp.CrossRefGoogle Scholar
Jimbo, M., A $q$ -analogue of $U\left(\mathfrak{gl}\left(N+1\right)\right)$ , Hecke algebras, and the Yang-Baxter equation , Lett. Math. Phys. 11 (1986), 247–252.CrossRefGoogle Scholar
Lusztig, G., Modular representations and quantum groups , Contemp. Math. 82 (1989) 59–77.CrossRefGoogle Scholar
Lusztig, G., Finite dimensional Hopf algebras arising from quantized universal enveloping algebras , J. Amer. Math. Soc. 3 (1990), 257–296.Google Scholar
Lusztig, G., Introduction to Quantum Groups, Progr. Math., 110, Birkhäuser/Springer, 1993.Google Scholar