THE PROJECTIVE DIMENSION OF THE EDGE IDEAL OF A VERY WELL-COVERED GRAPH

Abstract

A very well-covered graph is an unmixed graph whose covering number is half of the number of vertices. We construct an explicit minimal free resolution of the cover ideal of a Cohen–Macaulay very well-covered graph. Using this resolution, we characterize the projective dimension of the edge ideal of a very well-covered graph in terms of a pairwise $3$-disjoint set of complete bipartite subgraphs of the graph. We also show nondecreasing property of the projective dimension of symbolic powers of the edge ideal of a very well-covered graph with respect to the exponents.

1 Introduction

Let $G$ be a finite simple graph. We denote $V=V(G)$ the vertex set of $G$ and $E(G)$ the edge set of $G$ . Let $K$ be a field and $S=K[V]$ the polynomial ring whose variables are identified with the vertices of $G$ . We consider the standard (multi-)grading on $K[V]$ . We can associate with $G$ the ideal of $S$ :

$$\begin{eqnarray}\displaystyle I(G):=(x_{i}x_{j}:\{x_{i},x_{j}\}\in E(G)). & & \displaystyle \nonumber\end{eqnarray}$$

The ideal $I(G)$ is called the edge ideal of $G$ . Let $J(G)$ be the Alexander dual ideal of $I(G)$ . Actually, $J(G)$ is the cover ideal of $G$ , the ideal generated by all monomials which are products of the vertices of minimal vertex covers of $G$ . The main theme of the study of these ideals is to investigate the relations between the ring properties of $I(G)$ and $J(G)$ and the combinatorics of $G$ . We are interested in characterizing homological invariants of these ideals. There are some results about this direction; see for example, [3, 5, 7–13, 19, 21, 22] and the references therein.

A subset $C\subset V$ is called a vertex cover of $G$ if $C\cap e\neq \emptyset$ for each $e\in E(G)$ . A vertex cover is said to be minimal if it has no proper subset which is also a vertex cover. A graph $G$ is called unmixed if all minimal vertex covers of $G$ have the same cardinality. When $G$ is unmixed and has no isolated vertex, it is known that $2\operatorname{height}I(G)\geqslant \#V$ . When the equality holds, $G$ is called very well-covered. Note that the class of very well-covered graphs contains the class of unmixed bipartite graphs with no isolated vertex. Also the class of unmixed bipartite graphs contains the class of Cohen–Macaulay bipartite graphs. Here we say that a graph $G$ is Cohen–Macaulay if the quotient ring $S/I(G)$ is Cohen–Macaulay.

In general, it is hard to construct an explicit minimal free resolution of an ideal. But Herzog and Hibi [6] succeeded in constructing a resolution of $J(G)$ when $G$ is a Cohen–Macaulay bipartite graph. Also Mohammadi and Moradi [12] investigated a resolution of $J(G)$ when $G$ is an unmixed bipartite graph. The first main result of the present paper is a construction of an explicit minimal free resolution of $J(G)$ when $G$ is a Cohen–Macaulay very well-covered graph (Theorem 3.2).

Using our first main result, we derive the characterization of the projective dimension of $S/I(G)$ over $S$ , denoted by $\operatorname{pd}S/I(G)$ when $G$ is a very well-covered graph.

Two edges $\{x_{1},y_{1}\},\{x_{2},y_{2}\}\in E(G)$ are said to be $3$ -disjoint in $G$ if there is no other edge in $G$ between vertices $x_{1},x_{2},y_{1},y_{2}$ . Let ${\mathcal{B}}=\{B_{1},\ldots ,B_{r}\}$ be a set of complete bipartite subgraphs of $G$ . We set $V({\mathcal{B}})=V(B_{1})\cup \cdots \cup V(B_{r})$ . We say ${\mathcal{B}}$ is pairwise $3$ -disjoint if $V(B_{k})\cap V(B_{\ell })=\emptyset$ for any $k\neq \ell$ and there exists $e_{k}\in E(B_{k})$ for each $k=1,\ldots ,r$ such that $e_{1},\ldots ,e_{r}$ are pairwise $3$ -disjoint.

Theorem 1.1. Let $G$ be a very well-covered graph. Then

$$\begin{eqnarray}\displaystyle & & \displaystyle \operatorname{pd}S/I(G)=\nonumber\\ \displaystyle & & \displaystyle \quad \max \left\{\#V({\mathcal{B}})-r:\begin{array}{@{}l@{}}{\mathcal{B}}=\{B_{1},\ldots ,B_{r}\}\text{is a pairwise 3-disjoint set}\\ \text{of complete bipartite subgraphs of }G\end{array}\right\}.\nonumber\end{eqnarray}$$

Herzog and Hibi [6] characterized Cohen–Macaulay bipartite graphs in terms of the original graph. Crupi et al. [2] expanded their result for very well-covered graphs. When $G$ is an unmixed bipartite graph, Kummini [10, Proposition 3.2] gave a combinatorial characterization of $\operatorname{pd}S/I(G)$ . Later Kimura[9, Theorem 7.1] translated his result in terms of $G$ and Theorem 1.1 is a generalization of it. The characterization for the regularity of $I(G)$ , denoted by $\operatorname{reg}I(G)$ has already been done; Kummini [10] studied when $G$ is an unmixed bipartite graph and later Mahmoudi et al. [11] generalized Kummini’s result for a very well-covered graph $G$ . Theorem 1.1 stands the Alexander dual version of their generalization since $\operatorname{pd}S/I(G)=\operatorname{reg}J(G)$ ; see [18].

In this article we also treat the projective dimension of symbolic powers of the edge ideal of a very well-covered graph. The following problem is widely open:

Problem 1.2. Let $G$ be a graph. Then is it true that

$$\begin{eqnarray}\operatorname{pd}S/I(G)^{(i)}\geqslant \operatorname{pd}S/I(G)^{(i-1)}\end{eqnarray}$$

for $i\geqslant 2$ ?

We give a partial affirmative answer for the case that $G$ is a very well-covered graph. We also point out that the corresponding result also holds for Stanley depth.

Now we explain the organization of the paper. In Section 2, we recall the structure of a very well-covered graph which was given by Crupi et al. [2] and the association a very well-covered graph with semidirected graph by Mahmoudi et al. [11]. In Section 3, we construct an explicit minimal free resolution of $J(G)$ for a Cohen–Macaulay very well-covered graph $G$ and in Section 4, we prove Theorem 1.1. In Section 5, we show that the projective dimension of symbolic powers of the edge ideal of a very well-covered graph is nondecreasing.

2 The structure of very well-covered graphs

In this section, we recall the structure of very well-covered graphs. Almost all of the results in this section are proved by Crupi et al. [2] and Mahmoudi et al. [11].

Let $G$ be a finite simple graph with no isolated vertex. If $G$ is unmixed, then $2\operatorname{height}I(G)\geqslant \#V(G)$ is known. A graph $G$ is called very well-covered if $G$ is unmixed with $2\operatorname{height}I(G)=\#V(G)$ .

A subset $W\subset V(G)$ is called an independent set if there is no edge of $G$ between any two vertices in $W$ . An independent set is said to be maximal if it is maximal among independent sets of $G$ .

A very well-covered graph has the following structure.

Theorem 2.1. [2, Proposition 2.3]

Let $G$ be a very well-covered graph with height $h$ . Then there is a relabeling of vertices $V(G)=\{x_{1},\ldots ,x_{h},y_{1},\ldots ,y_{h}\}$ such that the following conditions are satisfied:

1. (i) $X=\{x_{1},\ldots ,x_{h}\}$ is a minimal vertex cover of $G$ and $Y=\{y_{1},\ldots ,y_{h}\}$ is a maximal independent set of $G$ ;

2. (ii) $\{x_{k},y_{k}\}\in E(G)$ for $k=1,\ldots ,h$ ;

3. (iii) if $\{z_{i},x_{j}\},\{y_{j},x_{k}\}\in E(G)$ , then $\{z_{i},x_{k}\}\in E(G)$ for distinct $i,j,k$ and for $z_{i}\in \{x_{i},y_{i}\}$ ;

4. (iv) if $\{x_{i},y_{j}\}\in E(G)$ , then $\{x_{i},x_{j}\}\notin E(G)$ .

On the other hand, the graph $G$ on $V=\{x_{1},\ldots ,x_{h},y_{1},\ldots ,y_{h}\}$ with (i), (ii), (iii), (iv) in Theorem 2.1 is a very well-covered graph.

Cohen–Macaulay very well-covered graphs have the following additional property.

Theorem 2.2. [2, Theorem 3.6]

Let $G$ be a very well-covered graph with height $h$ . Then $G$ is Cohen–Macaulay if and only if there is a relabeling of vertices $V(G)=\{x_{1},\ldots ,x_{h},y_{1},\ldots ,y_{h}\}$ with (i), (ii), (iii), (iv) of Theorem 2.1 and the following property:

1. (v) if $\{x_{i},y_{j}\}\in E(G)$ , then $i\leqslant j$ .

Now we associate a very well-covered graph $G$ with a semidirected graph $\mathfrak{d}_{G}$ as in [11]. We recall the notion of a semidirected graph. A semidirected graph $\mathfrak{d}$ consists of the vertex set $V(\mathfrak{d})=\{p_{1},\ldots ,p_{h}\}$ , the set of undirected edges $E_{u}(\mathfrak{d})$ , and the set of directed edges $E_{d}(\mathfrak{d})$ , where if $p_{i}p_{j}\in E_{d}(\mathfrak{d})$ , then $\{p_{i},p_{j}\}\notin E_{u}(\mathfrak{d})$ . We say $A\subset V(\mathfrak{d})$ is independent if $\{p_{i},p_{j}\}\notin E_{u}(\mathfrak{d})$ and $p_{i}p_{j},p_{j}p_{i}\notin E_{d}(\mathfrak{d})$ for any $p_{i},p_{j}\in A$ , $i\neq j$ . Let $\unicode[STIX]{x1D6E5}_{\mathfrak{d}}$ denote the set of all independent sets in $\mathfrak{d}$ . Then $\unicode[STIX]{x1D6E5}_{\mathfrak{d}}$ is a simplicial complex on $V(\mathfrak{d})$ and is called the independence complex of $\mathfrak{d}$ .

A semidirected graph $\mathfrak{d}$ is called acyclic if $\mathfrak{d}$ has no directed cycle and is called transitively closed if the following two properties are satisfied for any distinct $i,j,k$ :

1. (TC1) if $p_{i}p_{j}\in E_{d}(\mathfrak{d})$ and $p_{j}p_{k}\in E_{d}(\mathfrak{d})$ , then $p_{i}p_{k}\in E_{d}(\mathfrak{d})$ ;

2. (TC2) if $p_{i}p_{j}\in E_{d}(\mathfrak{d})$ and $\{p_{j},p_{k}\}\in E_{u}(\mathfrak{d})$ , then $\{p_{i},p_{k}\}\in E_{u}(\mathfrak{d})$ .

Let $\mathfrak{d}$ be an acyclic and transitively closed semidirected graph. We define $p_{j}\succ p_{i}$ if $p_{i}p_{j}\in E_{d}(\mathfrak{d})$ , and $p_{j}\succcurlyeq p_{i}$ if $p_{j}=p_{i}$ or $p_{j}\succ p_{i}$ . Then $\prec$ is a partial order on $V(\mathfrak{d})$ . For a subset $A\subset V(\mathfrak{d})$ , we define $p_{j}\succcurlyeq A$ if $p_{j}\succcurlyeq p_{i}$ for some $p_{i}\in A$ .

Let $\mathfrak{d}$ be a transitively closed semidirected graph. Two vertices $p_{i},p_{j}\in V(\mathfrak{d})$ are called strongly connected if $p_{i}p_{j},p_{j}p_{i}\in E_{d}(\mathfrak{d})$ . Let ${\mathcal{Z}}_{1},\ldots ,{\mathcal{Z}}_{t}$ be the strongly connected components of $\mathfrak{d}$ . Note that $V(\mathfrak{d})$ can be decomposed as ${\mathcal{Z}}_{1}\sqcup \cdots \sqcup {\mathcal{Z}}_{t}$ . Then we define a new semidirected graph $\widehat{\mathfrak{d}}$ , called the acyclic reduction of $\mathfrak{d}$ , as follows:

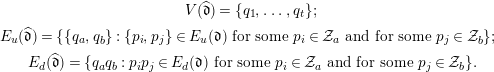$$\begin{eqnarray}\displaystyle & \displaystyle V(\widehat{\mathfrak{d}})=\{q_{1},\ldots ,q_{t}\}; & \displaystyle \nonumber\\ \displaystyle & \displaystyle \!\!E_{u}(\widehat{\mathfrak{d}})=\{\{q_{a},q_{b}\}:\{p_{i},p_{j}\}\in E_{u}(\mathfrak{d})\text{ for some }p_{i}\in {\mathcal{Z}}_{a}\text{ and for some }p_{j}\in {\mathcal{Z}}_{b}\}; & \displaystyle \nonumber\\ \displaystyle & \displaystyle E_{d}(\widehat{\mathfrak{d}})=\{q_{a}q_{b}:p_{i}p_{j}\in E_{d}(\mathfrak{d})\text{ for some }p_{i}\in {\mathcal{Z}}_{a}\text{ and for some }p_{j}\in {\mathcal{Z}}_{b}\}. & \displaystyle \nonumber\end{eqnarray}$$

Note that $\widehat{\mathfrak{d}}$ is acyclic. Also $\widehat{\mathfrak{d}}$ is transitively closed since $\mathfrak{d}$ is transitively closed.

Let $G$ be a very well-covered graph with (i), (ii), (iii), (iv) of Theorem 2.1. Then we define the semidirected graph $\mathfrak{d}_{G}$ as follows:

$$\begin{eqnarray}\displaystyle & \displaystyle V(\mathfrak{d}_{G})=\{p_{1},\ldots ,p_{h}\}; & \displaystyle \nonumber\\ \displaystyle & \displaystyle E_{u}(\mathfrak{d}_{G})=\{\{p_{i},p_{j}\}:\{x_{i},x_{j}\}\in E(G)\}; & \displaystyle \nonumber\\ \displaystyle & \displaystyle E_{d}(\mathfrak{d}_{G})=\{p_{i}p_{j}:\{x_{i},y_{j}\}\in E(G)\}. & \displaystyle \nonumber\end{eqnarray}$$

Note that $\mathfrak{d}_{G}$ is transitively closed. Now let us consider the acyclic reduction $\widehat{\mathfrak{d}_{G}}$ . We define a new graph $\widehat{G}$ , called the acyclic reduction of $G$ as follows:

$$\begin{eqnarray}\displaystyle V(\widehat{G}) & = & \displaystyle \{u_{1},\ldots ,u_{t}\}\cup \{v_{1},\ldots ,v_{t}\};\nonumber\\ \displaystyle E(\widehat{G}) & = & \displaystyle \{\{u_{a},v_{a}\}:a=1,\ldots ,t\}\nonumber\\ \displaystyle & \cup & \displaystyle \{\{u_{a},u_{b}\}:\{q_{a},q_{b}\}\in E_{u}(\widehat{\mathfrak{d}_{G}})\}\cup \{\{u_{a},v_{b}\}:q_{a}q_{b}\in E_{d}(\widehat{\mathfrak{d}_{G}})\}.\nonumber\end{eqnarray}$$

Then $\widehat{G}$ is a Cohen–Macaulay very well-covered graph [11, Lemma 4.5]. Note that $\mathfrak{d}_{\widehat{G}}=\widehat{\mathfrak{d}_{G}}$ and we denote it by $\widehat{\mathfrak{d}}_{G}$ .

For $\emptyset \neq \widehat{A}\in \unicode[STIX]{x1D6E5}_{\widehat{\mathfrak{d}}_{G}}$ , we set $\unicode[STIX]{x1D6FA}_{\widehat{A}}:=\bigcup _{q_{b}\succcurlyeq A}{\mathcal{Z}}_{b}$ and $\unicode[STIX]{x1D6FA}_{\emptyset }:=\emptyset$ .

Lemma 2.3. [11, Lemma 4.10]

Let $G$ be a very well-covered graph satisfying (i), (ii), (iii), (iv) of Theorem 2.1. Then

$$\begin{eqnarray}\displaystyle \operatorname{Ass}(S/I(G))=\{(x_{i}:p_{i}\notin \unicode[STIX]{x1D6FA}_{\widehat{A}})+(y_{i}:p_{i}\in \unicode[STIX]{x1D6FA}_{\widehat{A}}):\widehat{A}\in \unicode[STIX]{x1D6E5}_{\widehat{\mathfrak{d}}_{G}}\}. & & \displaystyle \nonumber\end{eqnarray}$$

Finally, we note the following lemma, which will be a key to the construction of a minimal free resolution of $J(G)$ when $G$ is a Cohen–Macaulay very well-covered graph; see the next section.

Lemma 2.4. [11, Lemma 4.9]

Let $G$ be a very well-covered graph satisfying (i), (ii), (iii), (iv) of Theorem 2.1. Then $\unicode[STIX]{x1D6FA}_{\widehat{A}}$ does not contain any undirected edge in $\mathfrak{d}_{G}$ for any $\widehat{A}\in \unicode[STIX]{x1D6E5}_{\widehat{\mathfrak{d}}_{G}}$ .

3 A minimal free resolution of $J(G)$ where $G$ is Cohen–Macaulay

The proof of Theorem 1.1 is inspired of that for the case of Cohen–Macaulay bipartite graphs in [9]. This proof is based on an explicit minimal free resolution of the cover ideal $J(G)$ given by Herzog and Hibi [6]. In this section, we construct an explicit minimal free resolution of $J(G)$ for a Cohen–Macaulay very well-covered graph $G$ . This is done by a similar construction to the one by Herzog and Hibi [6].

Let $G$ be a Cohen–Macaulay very well-covered graph on $V=\{x_{1},\ldots ,x_{h},y_{1},\ldots ,y_{h}\}$ with the properties (i), (ii), (iii), (iv) in Theorem 2.1 and (v) in Theorem 2.2. For $A\in \unicode[STIX]{x1D6E5}_{\mathfrak{d}_{G}}$ , we denote

$$\begin{eqnarray}\displaystyle u_{A}=\mathop{\prod }_{p_{i}\notin \unicode[STIX]{x1D6FA}_{A}}x_{i}\mathop{\prod }_{p_{i}\in \unicode[STIX]{x1D6FA}_{A}}y_{i}. & & \displaystyle \nonumber\end{eqnarray}$$

By Lemma 2.3, we know

$$\begin{eqnarray}\displaystyle J(G)=(u_{A}:A\in \unicode[STIX]{x1D6E5}_{\mathfrak{d}_{G}}). & & \displaystyle \nonumber\end{eqnarray}$$

Remark 3.1. Our notation of $x_{i},y_{j}$ are converse to the one in Herzog and Hibi [6]. Also “minimal” in our construction corresponds to “maximal” in that of [6].

We set ${\mathcal{L}}=\{\unicode[STIX]{x1D6FA}_{A}:A\in \unicode[STIX]{x1D6E5}_{\mathfrak{d}_{G}}\}$ . For $\unicode[STIX]{x1D6FA}\in {\mathcal{L}}$ , let $A(\unicode[STIX]{x1D6FA})$ denote the minimal elements in $\unicode[STIX]{x1D6FA}$ with respect to $\prec$ . Note that by Lemma 2.4, no two vertices in $\unicode[STIX]{x1D6FA}$ form an undirected edge in $\mathfrak{d}_{G}$ . It then follows that $A(\unicode[STIX]{x1D6FA})$ is independent in $\mathfrak{d}_{G}$ and the set $A(\unicode[STIX]{x1D6FA})$ is the unique face $A$ in $\unicode[STIX]{x1D6E5}_{\mathfrak{d}_{G}}$ with $\unicode[STIX]{x1D6FA}=\unicode[STIX]{x1D6FA}_{A}$ . Hence there is a one-to-one correspondence between $\unicode[STIX]{x1D6FA}\in {\mathcal{L}}$ and $A\in \unicode[STIX]{x1D6E5}_{\mathfrak{d}_{G}}$ .

Now we construct a ( $\mathbb{N}^{2h}$ -graded) minimal free resolution ${\mathcal{F}}_{\bullet }$ of $J(G)$ as follows. For all $i\geqslant 0$ , let ${\mathcal{F}}_{i}$ denote the free $S$ -module with basis $e(\unicode[STIX]{x1D6FA},T)$ , where $\unicode[STIX]{x1D6FA}\in {\mathcal{L}}$ and $T\subset V(\mathfrak{d}_{G})$ satisfying

$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FA}\cap T\subset A(\unicode[STIX]{x1D6FA}),\qquad \#(\unicode[STIX]{x1D6FA}\cap T)=i,\qquad \unicode[STIX]{x1D6FA}\cup T=V(\mathfrak{d}_{G}). & & \displaystyle \nonumber\end{eqnarray}$$

The degree of $e(\unicode[STIX]{x1D6FA},T)$ is defined by $\deg u_{A(\unicode[STIX]{x1D6FA}),T}$ where we define

$$\begin{eqnarray}\displaystyle u_{A,T}:=u_{A}\mathop{\prod }_{p_{i}\in \unicode[STIX]{x1D6FA}_{A}\cap T}x_{i}=\mathop{\prod }_{p_{i}\in \unicode[STIX]{x1D6FA}_{A}}y_{i}\mathop{\prod }_{p_{i}\notin \unicode[STIX]{x1D6FA}_{A}}x_{i}\mathop{\prod }_{p_{i}\in \unicode[STIX]{x1D6FA}_{A}\cap T}x_{i} & & \displaystyle \nonumber\end{eqnarray}$$

for $A\in \unicode[STIX]{x1D6E5}_{\mathfrak{d}_{G}}$ . Also for all $i\geqslant 1$ , we define the differential $\unicode[STIX]{x2202}_{i}:{\mathcal{F}}_{i}\longrightarrow {\mathcal{F}}_{i-1}$ by

$$\begin{eqnarray}\displaystyle \unicode[STIX]{x2202}_{i}(e(\unicode[STIX]{x1D6FA},T)):=\mathop{\sum }_{p_{\ell }\in \unicode[STIX]{x1D6FA}\cap T}(-1)^{\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FA}\cap T,p_{\ell })}(y_{\ell }e(\unicode[STIX]{x1D6FA}\setminus \{p_{\ell }\},T)-x_{\ell }e(\unicode[STIX]{x1D6FA},T\setminus \{p_{\ell }\})), & & \displaystyle \nonumber\end{eqnarray}$$

where for $Q\subset V(\mathfrak{d}_{G})$ and $p_{\ell }\in Q$ , we set $\unicode[STIX]{x1D70E}(Q,p_{\ell }):=\#\{p_{k}\in Q:k<\ell \}$ . Since $\unicode[STIX]{x1D6FA}$ contains no undirected edge in $\mathfrak{d}_{G}$ , we have that $\unicode[STIX]{x1D6FA}\setminus \{p_{\ell }\}=\unicode[STIX]{x1D6FA}_{A^{\prime }}\in {\mathcal{L}}$ where $A^{\prime }$ is the set of minimal elements of $\unicode[STIX]{x1D6FA}\setminus \{p_{\ell }\}$ with respect to $\prec$ and it is an independent set in $\mathfrak{d}_{G}$ . Then it is easy to see that $e(\unicode[STIX]{x1D6FA}\setminus \{p_{\ell }\},T),e(\unicode[STIX]{x1D6FA},T\setminus \{p_{\ell }\})$ are free bases of ${\mathcal{F}}_{i-1}$ and $\unicode[STIX]{x2202}_{i}$ possesses the multidegree.

The following is the main result of this section.

Theorem 3.2. $({\mathcal{F}}_{\bullet },\unicode[STIX]{x2202}_{\bullet })$ is a $\mathbb{N}^{2h}$ -graded minimal free resolution of $J(G)$ .

Before proving the theorem, we recall some notion on graphs. Let $G$ be a simple graph on the vertex set $V$ . Take $W\subset V$ . The induced subgraph of $G$ on $W$ is the graph whose vertex set is $W$ and whose edge set is the set of all edges of $G$ whose two end vertices are in $W$ . Also, $G\setminus W$ denotes the induced subgraph $G_{V\setminus W}$ . For $x\in V$ , we denote by $N_{G}(x)$ the set of neighbors of $x$ in $G$ : $N_{G}(x):=\{y\in V:\{x,y\}\in E(G)\}$ .

Proof of Theorem 3.2.

We use arguments similar to those of Herzog and Hibi [6, Theorem 2.1].

Set $V^{\prime }:=V(\mathfrak{d}_{G})$ . The free basis $e(\unicode[STIX]{x1D6FA},T)$ of ${\mathcal{F}}_{0}$ satisfies $\unicode[STIX]{x1D6FA}\cap T=\emptyset$ and $\unicode[STIX]{x1D6FA}\cup T=V^{\prime }$ . Thus $T$ is uniquely determined by $\unicode[STIX]{x1D6FA}\in {\mathcal{L}}$ : $T=V^{\prime }\setminus \unicode[STIX]{x1D6FA}$ . Also $\deg e(\unicode[STIX]{x1D6FA},T)=\deg u_{\unicode[STIX]{x1D6FA},T}=\deg u_{A(\unicode[STIX]{x1D6FA})}$ . Define the augmentation $\unicode[STIX]{x1D700}:{\mathcal{F}}_{0}\longrightarrow J(G)$ by $e(\unicode[STIX]{x1D6FA},T)\mapsto u_{A(\unicode[STIX]{x1D6FA})}$ .

Claim 1. ${\mathcal{F}}_{1}\stackrel{\unicode[STIX]{x2202}_{1}}{\longrightarrow }{\mathcal{F}}_{0}\stackrel{\unicode[STIX]{x1D700}}{\longrightarrow }J(G)\longrightarrow 0$ is a complex.

Take a free basis $e(\unicode[STIX]{x1D6FA},T)$ of ${\mathcal{F}}_{1}$ . Note that $\#(\unicode[STIX]{x1D6FA}\cap T)=1$ and set $\unicode[STIX]{x1D6FA}\cap T=\{p_{\ell }\}$ . Then

$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D700}\circ \unicode[STIX]{x2202}_{1}(e(\unicode[STIX]{x1D6FA},T)) & = & \displaystyle \unicode[STIX]{x1D700}(y_{\ell }e(\unicode[STIX]{x1D6FA}\setminus \{p_{\ell }\},T)-x_{\ell }e(\unicode[STIX]{x1D6FA},T\setminus \{p_{\ell }\}))\nonumber\\ \displaystyle & = & \displaystyle y_{\ell }u_{A(\unicode[STIX]{x1D6FA}\setminus \{p_{\ell }\})}-x_{\ell }u_{A(\unicode[STIX]{x1D6FA})}=0,\nonumber\end{eqnarray}$$

as desired.

Claim 2. $\unicode[STIX]{x2202}_{i}\circ \unicode[STIX]{x2202}_{i-1}=0$ .

Note that

$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x2202}_{i}\circ \unicode[STIX]{x2202}_{i-1}(e(\unicode[STIX]{x1D6FA},T))\nonumber\\ \displaystyle & & \displaystyle \quad =\unicode[STIX]{x2202}_{i}\left(\mathop{\sum }_{p_{\ell }\in \unicode[STIX]{x1D6FA}\cap T}(-1)^{\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FA}\cap T,p_{\ell })}(y_{\ell }e(\unicode[STIX]{x1D6FA}\setminus \{p_{\ell }\},T)-x_{\ell }e(\unicode[STIX]{x1D6FA},T\setminus \{p_{\ell }\}))\right)\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{p_{\ell }\in \unicode[STIX]{x1D6FA}\cap T}(-1)^{\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FA}\cap T,p_{\ell })}\nonumber\\ \displaystyle & & \displaystyle \qquad \times \left[y_{\ell }\mathop{\sum }_{\substack{ p_{k}\in \unicode[STIX]{x1D6FA}\cap T \\ k\neq \ell }}(-1)^{\unicode[STIX]{x1D70E}((\unicode[STIX]{x1D6FA}\setminus \{p_{\ell }\})\cap T,p_{k})}\right.\nonumber\\ \displaystyle & & \displaystyle \qquad \qquad \times \,(y_{k}e(\unicode[STIX]{x1D6FA}\setminus \{p_{\ell },p_{k}\},T)-x_{k}e(\unicode[STIX]{x1D6FA}\setminus \{p_{\ell }\},T\setminus \{p_{k}\}))\nonumber\\ \displaystyle & & \displaystyle \qquad \qquad -\,x_{\ell }\mathop{\sum }_{\substack{ p_{k}\in \unicode[STIX]{x1D6FA}\cap T \\ k\neq \ell }}(-1)^{\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FA}\cap (T\setminus \{p_{\ell }\}),p_{k})}\nonumber\\ \displaystyle & & \displaystyle \qquad \qquad \times \left.(y_{k}e(\unicode[STIX]{x1D6FA}\setminus \{p_{k}\},T\setminus \{p_{\ell }\})-x_{k}e(\unicode[STIX]{x1D6FA},T\setminus \{p_{\ell },p_{k}\}))\right].\nonumber\end{eqnarray}$$

Then the coefficient of $e(\unicode[STIX]{x1D6FA}\setminus \{p_{\ell },p_{k}\},T)$ , $k\neq \ell$ vanishes since the differences of $\unicode[STIX]{x1D70E}((\unicode[STIX]{x1D6FA}\setminus \{p_{\ell }\})\cap T,p_{k})$ and $\unicode[STIX]{x1D70E}((\unicode[STIX]{x1D6FA}\setminus \{p_{k}\})\cap T,p_{\ell })$ is just $1$ . Similarly, the coefficient of $e(\unicode[STIX]{x1D6FA},T\setminus \{p_{\ell },p_{k}\})$ , $k\neq \ell$ vanishes. Finally we check the coefficient of $e(\unicode[STIX]{x1D6FA}\setminus \{p_{\ell }\},T\setminus \{p_{k}\})$ . In this case, $\unicode[STIX]{x1D70E}((\unicode[STIX]{x1D6FA}\setminus \{p_{\ell }\})\cap T,p_{k})$ and $\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D6FA}\cap (T\setminus \{p_{k}\}),p_{\ell })$ also differ just by $1$ . Therefore, we have $\unicode[STIX]{x2202}_{i}\circ \unicode[STIX]{x2202}_{i-1}(e(\unicode[STIX]{x1D6FA},T))=0$ .

Claim 3. ${\mathcal{F}}_{1}\stackrel{\unicode[STIX]{x2202}_{1}}{\longrightarrow }{\mathcal{F}}_{0}\stackrel{\unicode[STIX]{x1D700}}{\longrightarrow }J(G)\longrightarrow 0$ is exact.

We first note that the first syzygy module of $J(G)$ is generated by

$$\begin{eqnarray}\displaystyle r_{\unicode[STIX]{x1D6FA},\unicode[STIX]{x1D6E9}}:=y_{\unicode[STIX]{x1D6E9}\setminus \unicode[STIX]{x1D6FA}}x_{\unicode[STIX]{x1D6FA}\setminus \unicode[STIX]{x1D6E9}}e(\unicode[STIX]{x1D6FA},V^{\prime }\setminus \unicode[STIX]{x1D6FA})-y_{\unicode[STIX]{x1D6FA}\setminus \unicode[STIX]{x1D6E9}}x_{\unicode[STIX]{x1D6E9}\setminus \unicode[STIX]{x1D6FA}}e(\unicode[STIX]{x1D6E9},V^{\prime }\setminus \unicode[STIX]{x1D6E9}),\quad \unicode[STIX]{x1D6FA},\unicode[STIX]{x1D6E9}\in {\mathcal{L}}, & & \displaystyle \nonumber\end{eqnarray}$$

where for $\unicode[STIX]{x1D6FA}\subset V^{\prime }$ , we denote

$$\begin{eqnarray}\displaystyle x_{\unicode[STIX]{x1D6FA}}:=\mathop{\prod }_{p_{\ell }\in \unicode[STIX]{x1D6FA}}x_{\ell }\qquad \text{and}\qquad y_{\unicode[STIX]{x1D6FA}}:=\mathop{\prod }_{p_{\ell }\in \unicode[STIX]{x1D6FA}}y_{\ell }. & & \displaystyle \nonumber\end{eqnarray}$$

For $\unicode[STIX]{x1D6FA},\unicode[STIX]{x1D6E9}\in {\mathcal{L}}$ , the intersection $\unicode[STIX]{x1D6FA}\cap \unicode[STIX]{x1D6E9}$ is in ${\mathcal{L}}$ because $\unicode[STIX]{x1D6FA}\cap \unicode[STIX]{x1D6E9}=\unicode[STIX]{x1D6FA}_{A^{\prime }}$ where $A^{\prime }$ is the set of minimal elements of $\unicode[STIX]{x1D6FA}\cap \unicode[STIX]{x1D6E9}$ with respect to $\prec$ . Also we can easily check that

$$\begin{eqnarray}\displaystyle r_{\unicode[STIX]{x1D6FA},\unicode[STIX]{x1D6E9}}=y_{\unicode[STIX]{x1D6E9}\setminus \unicode[STIX]{x1D6FA}}r_{\unicode[STIX]{x1D6FA},\unicode[STIX]{x1D6FA}\cap \unicode[STIX]{x1D6E9}}-y_{\unicode[STIX]{x1D6FA}\setminus \unicode[STIX]{x1D6E9}}r_{\unicode[STIX]{x1D6E9},\unicode[STIX]{x1D6FA}\cap \unicode[STIX]{x1D6E9}}. & & \displaystyle \nonumber\end{eqnarray}$$

Therefore, in order to prove the claim, it is sufficient to prove that $r_{\unicode[STIX]{x1D6FA},\unicode[STIX]{x1D6E9}}\in \unicode[STIX]{x2202}_{1}({\mathcal{F}}_{1})$ for $\unicode[STIX]{x1D6FA},\unicode[STIX]{x1D6E9}\in {\mathcal{L}}$ with $\unicode[STIX]{x1D6E9}\subset \unicode[STIX]{x1D6FA}$ ; let $\unicode[STIX]{x1D6FA},\unicode[STIX]{x1D6E9}\in {\mathcal{L}}$ be such a pair. Set $\unicode[STIX]{x1D6FA}\setminus \unicode[STIX]{x1D6E9}=\{p_{k_{1}},\ldots ,p_{k_{m}}\}$ , where $k_{1}>\cdots >k_{m}$ , and

$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D6FA}_{0}=\unicode[STIX]{x1D6E9}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \unicode[STIX]{x1D6FA}_{j}=\unicode[STIX]{x1D6FA}_{j-1}\cup \{p_{k_{j}}\},\quad j=1,\ldots ,m. & \displaystyle \nonumber\end{eqnarray}$$

We show that $\unicode[STIX]{x1D6FA}_{j}\in {\mathcal{L}}$ for each $j$ .

Let $A_{j}$ denote the set of minimal elements of $\unicode[STIX]{x1D6FA}_{j}$ . We prove $\unicode[STIX]{x1D6FA}_{j}=\unicode[STIX]{x1D6FA}_{A_{j}}$ . It is enough to show that $\unicode[STIX]{x1D6FA}_{j}\supset \unicode[STIX]{x1D6FA}_{A_{j}}$ . Take $p_{\ell }\in \unicode[STIX]{x1D6FA}_{A_{j}}$ . Then there exists $p_{k}\in A_{j}$ with $p_{k}\preccurlyeq p_{\ell }$ . We note that $k\leqslant \ell$ by the property (v) of Theorem 2.2. We also note that $p_{k}\in A_{j}\subset \unicode[STIX]{x1D6FA}_{j}\subset \unicode[STIX]{x1D6FA}$ , and combining this with $\unicode[STIX]{x1D6FA}\in {\mathcal{L}}$ , we have $p_{\ell }\in \unicode[STIX]{x1D6FA}$ . By the same reason, when $p_{k}\in \unicode[STIX]{x1D6E9}$ , we have $p_{\ell }\in \unicode[STIX]{x1D6E9}$ . Since $\unicode[STIX]{x1D6E9}\subset \unicode[STIX]{x1D6FA}_{j}$ , we have done for the case $p_{k}\in \unicode[STIX]{x1D6E9}$ . Thus we assume $p_{k}\notin \unicode[STIX]{x1D6E9}$ . If $p_{\ell }\in \unicode[STIX]{x1D6E9}$ , then $p_{\ell }\in \unicode[STIX]{x1D6FA}_{j}$ is obvious. If $p_{\ell }\notin \unicode[STIX]{x1D6E9}$ , it follows that $p_{k},p_{\ell }\in \unicode[STIX]{x1D6FA}\setminus \unicode[STIX]{x1D6E9}$ . Since $\ell \geqslant k$ and $p_{k}\in \unicode[STIX]{x1D6FA}_{j}$ , we conclude that $p_{\ell }\in \unicode[STIX]{x1D6FA}_{j}$ by the construction of $\unicode[STIX]{x1D6FA}_{j}$ .

Note that $p_{k_{j}}$ must be a minimal element of $\unicode[STIX]{x1D6FA}_{j}$ and

$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FA}_{j}\cap (V^{\prime }\setminus \unicode[STIX]{x1D6FA}_{j-1}) & = & \displaystyle (\unicode[STIX]{x1D6E9}\cup \{p_{k_{1}},\ldots ,p_{k_{j}}\})\nonumber\\ \displaystyle & \cap & \displaystyle (V^{\prime }\setminus (\unicode[STIX]{x1D6E9}\cup \{p_{k_{1}},\ldots ,p_{k_{j-1}}\}))=\{p_{k_{j}}\}.\nonumber\end{eqnarray}$$

By the easy calculation, we have

$$\begin{eqnarray}\displaystyle & \displaystyle r_{\unicode[STIX]{x1D6FA},\unicode[STIX]{x1D6E9}}=\mathop{\sum }_{j=1}^{m}\left(\mathop{\prod }_{s=j+1}^{m}y_{k_{s}}\mathop{\prod }_{s=1}^{j-1}x_{k_{s}}\right)r_{\unicode[STIX]{x1D6FA}_{j},\unicode[STIX]{x1D6FA}_{j-1}}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle r_{\unicode[STIX]{x1D6FA}_{j},\unicode[STIX]{x1D6FA}_{j-1}}=-\unicode[STIX]{x2202}(e(\unicode[STIX]{x1D6FA}_{j},V^{\prime }\setminus \unicode[STIX]{x1D6FA}_{j-1})),\quad j=1,\ldots ,m. & \displaystyle \nonumber\end{eqnarray}$$

Therefore, the claim follows.

Claim 4. $({\mathcal{F}}_{\bullet },\unicode[STIX]{x2202}_{\bullet })$ is acyclic.

We proceed by induction on $h$ .

If $h=1$ , the cover ideal $J(G)=(x_{1},y_{1})$ . Then $({\mathcal{F}}_{\bullet },\unicode[STIX]{x2202}_{\bullet })$ is just the Koszul complex associated with $\{x_{1},y_{1}\}$ and thus it is acyclic.

Now we assume $h>1$ . The induced subgraph $G^{\prime }:=G_{V\setminus \{x_{1},y_{1}\}}$ is also a Cohen–Macaulay very well-covered graph. Note that $G^{\prime }$ satisfies the properties (i), (ii), (iii), (iv) of Theorem 2.1 and (v) of Theorem 2.2 with respect to the induced labeling from $G$ . Let $({\mathcal{F}}^{\prime },\unicode[STIX]{x2202}^{\prime })$ denote the complex corresponding to $G^{\prime }$ . Then by inductive hypothesis, $({\mathcal{F}}^{\prime },\unicode[STIX]{x2202}^{\prime })$ is acyclic. Since the inclusion $K[V(G^{\prime })]\longrightarrow K[V(G)]$ is a flat extension, by tensoring $K[V(G)]$ to $({\mathcal{F}}^{\prime },\unicode[STIX]{x2202}^{\prime })$ , we obtain the acyclic complex over $K[V(G)]$ . We define the map $\unicode[STIX]{x1D719}:{\mathcal{F}}^{\prime }\longrightarrow {\mathcal{F}}$ by $e(\unicode[STIX]{x1D6FA},T)\mapsto e(\unicode[STIX]{x1D6FA},T\cup \{p_{1}\})$ . Then $\unicode[STIX]{x1D719}$ is an injective map of complexes. Also the induced map $J(G^{\prime })=H_{0}({\mathcal{F}}^{\prime })\longrightarrow H_{0}({\mathcal{F}})=J(G)$ is a multiplication by $x_{1}$ . Let ${\mathcal{G}}_{\bullet }$ be the quotient complex ${\mathcal{F}}/{\mathcal{F}}^{\prime }$ . Then the short exact sequence of complexes

$$\begin{eqnarray}\displaystyle 0\longrightarrow {\mathcal{F}}^{\prime }\longrightarrow {\mathcal{F}}\longrightarrow {\mathcal{G}}\longrightarrow 0 & & \displaystyle \nonumber\end{eqnarray}$$

induces the long exact sequence

$$\begin{eqnarray}\displaystyle \cdots \longrightarrow H_{2}({\mathcal{G}})\longrightarrow H_{1}({\mathcal{F}}^{\prime })\longrightarrow H_{1}({\mathcal{F}})\longrightarrow H_{1}({\mathcal{G}})\longrightarrow H_{0}({\mathcal{F}}^{\prime })\stackrel{\cdot x_{1}}{\longrightarrow }H_{0}({\mathcal{F}}). & & \displaystyle \nonumber\end{eqnarray}$$

By inductive hypothesis, ${\mathcal{F}}^{\prime }$ is acyclic, that is, $H_{i}({\mathcal{F}}^{\prime })=0$ for all $i>0$ . Also the multiplication map is injective. It then follows that $H_{i}({\mathcal{F}})\cong H_{i}({\mathcal{G}})$ for all $i>0$ . We prove $H_{i}({\mathcal{G}})=0$ for all $i>0$ .

We consider the induced subgraph $G^{\prime \prime }:=G_{V\setminus (\{x_{1}\}\cup N_{G}(x_{1}))}$ . Let $G_{0}^{\prime \prime }:=G^{\prime \prime }\setminus \{\text{isolated vertices of }G^{\prime \prime }\}$ . It was proved by Mahmoudi et al. in [11, Proof of Theorem 3.2] that $G_{0}^{\prime \prime }$ is also a Cohen–Macaulay very well-covered graph with respect to the induced labeling of the vertices from $G$ . Let $({\mathcal{F}}^{\prime \prime },\unicode[STIX]{x2202}^{\prime \prime })$ denote the complex corresponding to $G_{0}^{\prime \prime }$ . Similarly to the case of $({\mathcal{F}}^{\prime },\unicode[STIX]{x2202}^{\prime })$ , we do not distinguish $({\mathcal{F}}^{\prime \prime },\unicode[STIX]{x2202}^{\prime \prime })$ with $({\mathcal{F}}^{\prime \prime }\otimes K[V(G)],\unicode[STIX]{x2202}^{\prime \prime }\otimes 1)$ . Let ${\mathcal{C}}_{\bullet }$ denote the mapping cone of the complex homomorphism

$$\begin{eqnarray}\displaystyle {\mathcal{F}}^{\prime \prime }\stackrel{\cdot -x_{1}}{\longrightarrow }{\mathcal{F}}^{\prime \prime }. & & \displaystyle \nonumber\end{eqnarray}$$

Then we have a short exact sequence of complexes

$$\begin{eqnarray}\displaystyle 0\longrightarrow {\mathcal{F}}^{\prime \prime }\longrightarrow {\mathcal{C}}\longrightarrow {\mathcal{F}}^{\prime \prime }[-1]\longrightarrow 0, & & \displaystyle \nonumber\end{eqnarray}$$

where $({\mathcal{F}}^{\prime \prime }[-1])_{i}:={\mathcal{F}}_{i-1}^{\prime \prime }$ . This induces the long exact sequence

$$\begin{eqnarray}\displaystyle & \displaystyle \cdots \longrightarrow H_{2}({\mathcal{C}})\longrightarrow H_{1}({\mathcal{F}}^{\prime \prime }) & \displaystyle \nonumber\\ \displaystyle & \displaystyle \stackrel{\cdot -x_{1}}{\longrightarrow }H_{1}({\mathcal{F}}^{\prime \prime })\longrightarrow H_{1}({\mathcal{C}})\longrightarrow H_{0}({\mathcal{F}}^{\prime \prime }) & \displaystyle \nonumber\\ \displaystyle & \displaystyle \stackrel{\cdot -x_{1}}{\longrightarrow }H_{0}({\mathcal{F}}^{\prime \prime })\longrightarrow H_{0}({\mathcal{C}})\longrightarrow 0. & \displaystyle \nonumber\end{eqnarray}$$

By inductive hypothesis, the complex ${\mathcal{F}}^{\prime \prime }$ is also acyclic, and the multiplication map $J(G^{\prime \prime })=H_{0}({\mathcal{F}}^{\prime \prime })\stackrel{\cdot -x_{1}}{\longrightarrow }H_{0}({\mathcal{F}}^{\prime \prime })=J(G^{\prime \prime })$ is injective, we have $H_{i}({\mathcal{C}})=0$ for $i\geqslant 1$ .

Finally we prove that ${\mathcal{C}}\cong {\mathcal{G}}$ . Note that

$$\begin{eqnarray}\displaystyle {\mathcal{C}}_{\ell }={{\mathcal{F}}^{\prime \prime }}_{\ell -1}\oplus {{\mathcal{F}}^{\prime \prime }}_{\ell },\quad \ell \geqslant 0, & & \displaystyle \nonumber\end{eqnarray}$$

where ${{\mathcal{F}}^{\prime \prime }}_{-1}=0$ . Set ${\mathcal{L}}^{\prime \prime }=\{\unicode[STIX]{x1D6FA}_{A^{\prime \prime }}^{\prime \prime }:A^{\prime \prime }\in \mathfrak{d}_{G_{0}^{\prime \prime }}\}$ . Then the free basis of ${\mathcal{C}}_{\ell }$ is $\mathfrak{C}_{\ell }=\mathfrak{B}_{\ell -1}\cup \mathfrak{B}_{\ell }$ where

$$\begin{eqnarray}\displaystyle \mathfrak{B}_{\ell }=\left\{e(\unicode[STIX]{x1D6FA}^{\prime \prime },T^{\prime \prime }):\begin{array}{@{}l@{}}\unicode[STIX]{x1D6FA}^{\prime \prime }\in {\mathcal{L}}^{\prime \prime },T^{\prime \prime }\subset V(\mathfrak{d}_{G_{0}^{\prime \prime }}),\\ \unicode[STIX]{x1D6FA}^{\prime \prime }\cap T^{\prime \prime }\subset A(\unicode[STIX]{x1D6FA}^{\prime \prime }),\#(\unicode[STIX]{x1D6FA}^{\prime \prime }\cap T^{\prime \prime })=\ell ,\unicode[STIX]{x1D6FA}^{\prime \prime }\cup T^{\prime \prime }=V(\mathfrak{d}_{G_{0}^{\prime \prime }})\end{array}\right\}. & & \displaystyle \nonumber\end{eqnarray}$$

On the other hand, the free basis of ${\mathcal{G}}_{\ell }$ is

$$\begin{eqnarray}\displaystyle \mathfrak{G}_{\ell }:=\left\{e(\unicode[STIX]{x1D6FA},T):\begin{array}{@{}l@{}}\unicode[STIX]{x1D6FA}\in {\mathcal{L}},p_{1}\in \unicode[STIX]{x1D6FA},T\subset V(\mathfrak{d}_{G}),\\ \unicode[STIX]{x1D6FA}\cap T\subset A(\unicode[STIX]{x1D6FA}),\#(\unicode[STIX]{x1D6FA}\cap T)=\ell ,\unicode[STIX]{x1D6FA}\cup T=V(\mathfrak{d}_{G})\end{array}\right\}. & & \displaystyle \nonumber\end{eqnarray}$$

We define $K[V(G)]$ -linear homomorphism $\unicode[STIX]{x1D713}_{\ell }:{\mathcal{C}}_{\ell }\longrightarrow {\mathcal{G}}_{\ell }$ by

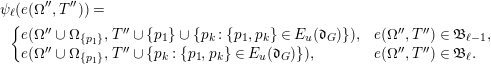$$\begin{eqnarray}\displaystyle & & \displaystyle \!\!\!\unicode[STIX]{x1D713}_{\ell }(e(\unicode[STIX]{x1D6FA}^{\prime \prime },T^{\prime \prime }))=\nonumber\\ \displaystyle & & \displaystyle \left\{\begin{array}{@{}ll@{}}e(\unicode[STIX]{x1D6FA}^{\prime \prime }\cup \unicode[STIX]{x1D6FA}_{\{p_{1}\}},T^{\prime \prime }\cup \{p_{1}\}\cup \{p_{k}:\{p_{1},p_{k}\}\in E_{u}(\mathfrak{d}_{G})\}), & e(\unicode[STIX]{x1D6FA}^{\prime \prime },T^{\prime \prime })\in \mathfrak{B}_{\ell -1},\\ e(\unicode[STIX]{x1D6FA}^{\prime \prime }\cup \unicode[STIX]{x1D6FA}_{\{p_{1}\}},T^{\prime \prime }\cup \{p_{k}:\{p_{1},p_{k}\}\in E_{u}(\mathfrak{d}_{G})\}), & e(\unicode[STIX]{x1D6FA}^{\prime \prime },T^{\prime \prime })\in \mathfrak{B}_{\ell }.\end{array}\right.\nonumber\end{eqnarray}$$

Then $\unicode[STIX]{x1D713}_{\ell }$ is well-defined. Note that $A(\unicode[STIX]{x1D6FA}^{\prime \prime }\cup \unicode[STIX]{x1D6FA}_{\{p_{1}\}})=A(\unicode[STIX]{x1D6FA}^{\prime \prime })\cup \{p_{1}\}$ and $T^{\prime \prime }\cap \{p_{1}\}=\emptyset$ . It is easy to see that all $\unicode[STIX]{x1D713}_{\ell }$ are bijective and $(\unicode[STIX]{x1D713}_{\ell })$ induces an isomorphism of complexes.◻

Remark 3.3. In [11, Lemma 3.4], Mahmoudi et al. characterized the regularity of a Cohen–Macaulay very well-covered graph by using $G^{\prime }$ and $G^{\prime \prime }$ (the notations are $G_{2}$ , $G_{1}$ , respectively).

By the above explicit minimal free resolution of $J(G)$ , we obtain the nonzero extremal Betti numbers of $J(G)$ . Recall that $\unicode[STIX]{x1D6FD}_{i,\unicode[STIX]{x1D70E}}(J(G))$ is extremal if $\unicode[STIX]{x1D6FD}_{j,\unicode[STIX]{x1D70F}}(J(G))=0$ for all $j\geqslant i$ and $\unicode[STIX]{x1D70F}\succ \unicode[STIX]{x1D70E}$ with $|\unicode[STIX]{x1D70F}|-|\unicode[STIX]{x1D70E}|\geqslant j-i$ , where $|\unicode[STIX]{x1D70E}|=\unicode[STIX]{x1D70E}_{1}+\cdots +\unicode[STIX]{x1D70E}_{n}$ for $\unicode[STIX]{x1D70E}\in \mathbb{N}^{n}$ .

Corollary 3.4. The free basis $e(\unicode[STIX]{x1D6FA},T)$ corresponds to an extremal Betti number of $J(G)$ if and only if the following two conditions are satisfied:

1. (i) $A(\unicode[STIX]{x1D6FA})$ is a facet of $\unicode[STIX]{x1D6E5}_{\mathfrak{d}_{G}}$ ;

2. (ii) $\unicode[STIX]{x1D6FA}\cap T=A(\unicode[STIX]{x1D6FA})$ .

Proof. We use the same notation as above.

We first assume that $e(\unicode[STIX]{x1D6FA},T)$ corresponds to an extremal Betti number of $J(G)$ . Suppose $\unicode[STIX]{x1D6FA}\cap T\neq A(\unicode[STIX]{x1D6FA})$ . We set $A^{\prime }:=A(\unicode[STIX]{x1D6FA})\setminus (\unicode[STIX]{x1D6FA}\cap T)$ and $S:=T\cup A^{\prime }$ . Then the degree of $e(\unicode[STIX]{x1D6FA},S)$ is

$$\begin{eqnarray}\displaystyle \deg e(\unicode[STIX]{x1D6FA},S) & = & \displaystyle \deg \mathop{\prod }_{p_{i}\in \unicode[STIX]{x1D6FA}}y_{i}\mathop{\prod }_{p_{i}\notin \unicode[STIX]{x1D6FA}}x_{i}\mathop{\prod }_{p_{i}\in \unicode[STIX]{x1D6FA}\cap S}x_{i}\nonumber\\ \displaystyle & = & \displaystyle \deg \mathop{\prod }_{p_{i}\in \unicode[STIX]{x1D6FA}}y_{i}\mathop{\prod }_{p_{i}\notin \unicode[STIX]{x1D6FA}}x_{i}\mathop{\prod }_{p_{i}\in \unicode[STIX]{x1D6FA}\cap T}x_{i}\mathop{\prod }_{p_{i}\in A^{\prime }}x_{i}\nonumber\\ \displaystyle & = & \displaystyle \deg e(\unicode[STIX]{x1D6FA},T)+\deg \mathop{\prod }_{p_{i}\in A^{\prime }}x_{i}.\nonumber\end{eqnarray}$$

Hence $e(\unicode[STIX]{x1D6FA},T)$ does not correspond to an extremal Betti number, a contradiction. Therefore, we assume $\unicode[STIX]{x1D6FA}\cap T=A(\unicode[STIX]{x1D6FA})$ . Suppose that $A(\unicode[STIX]{x1D6FA})$ is not a facet. Then there exists $p_{i}\in V(\mathfrak{d}_{G})$ with $A(\unicode[STIX]{x1D6FA})\cup \{p_{i}\}\in \unicode[STIX]{x1D6E5}_{\mathfrak{d}_{G}}$ . Let $p_{i_{0}}$ be such a vertex with maximum index. Set $\unicode[STIX]{x1D6E9}:=\unicode[STIX]{x1D6FA}_{A(\unicode[STIX]{x1D6FA})\cup \{p_{i_{0}}\}}$ and $S=T\cup \{p_{i_{0}}\}$ . We claim $\unicode[STIX]{x1D6E9}=\unicode[STIX]{x1D6FA}\cup \{p_{i_{0}}\}$ . Indeed, $\unicode[STIX]{x1D6E9}\supset \unicode[STIX]{x1D6FA}\cup \{p_{i_{0}}\}$ is obvious. Conversely, assume $p_{k}\in \unicode[STIX]{x1D6E9}$ . If $p_{k}\succcurlyeq p_{\ell }$ for some $p_{\ell }\in A(\unicode[STIX]{x1D6FA})$ , then $p_{k}\in \unicode[STIX]{x1D6FA}$ . Otherwise, by applying Lemma 2.4 to $\unicode[STIX]{x1D6E9}=\unicode[STIX]{x1D6FA}_{A(\unicode[STIX]{x1D6FA})\cup \{p_{i_{0}}\}}$ , we have $\{p_{k}\}\cup A(\unicode[STIX]{x1D6FA})\in \unicode[STIX]{x1D6E5}_{\mathfrak{d}_{G}}$ . On the other hand, $p_{k}\succcurlyeq p_{i_{0}}$ also satisfied. In particular $i_{0}\leqslant k$ . Then the maximality of $i_{0}$ implies that $p_{i_{0}}=p_{k}$ , as desired. Hence

$$\begin{eqnarray}\displaystyle \deg e(\unicode[STIX]{x1D6E9},S) & = & \displaystyle \deg \mathop{\prod }_{p_{i}\in \unicode[STIX]{x1D6E9}}y_{i}\mathop{\prod }_{p_{i}\notin \unicode[STIX]{x1D6E9}}x_{i}\mathop{\prod }_{p_{i}\in \unicode[STIX]{x1D6E9}\cap S}x_{i}\nonumber\\ \displaystyle & = & \displaystyle \deg y_{i_{0}}\mathop{\prod }_{p_{i}\in \unicode[STIX]{x1D6FA}}y_{i}\mathop{\prod }_{p_{i}\notin \unicode[STIX]{x1D6FA}}x_{i}\mathop{\prod }_{p_{i}\in \unicode[STIX]{x1D6FA}\cap T}x_{i}\nonumber\\ \displaystyle & = & \displaystyle \deg e(\unicode[STIX]{x1D6FA},T)+\deg y_{i_{0}}.\nonumber\end{eqnarray}$$

This is also a contradiction.

Next, let $e(\unicode[STIX]{x1D6FA},T)$ be a free basis of ${\mathcal{F}}_{\ell }$ of degree $\unicode[STIX]{x1D70E}$ satisfying the conditions (i), (ii). Suppose that there is a free basis $e(\unicode[STIX]{x1D6E9},S)$ of ${\mathcal{F}}_{k}$ of degree $\unicode[STIX]{x1D70F}$ with $k\geqslant \ell$ , $\unicode[STIX]{x1D70F}\succ \unicode[STIX]{x1D70E}$ , and $|\unicode[STIX]{x1D70F}|-|\unicode[STIX]{x1D70E}|\geqslant k-\ell$ . Note that $J(G)$ has a linear resolution, and thus $|\unicode[STIX]{x1D70F}|-|\unicode[STIX]{x1D70E}|=k-\ell$ . Since

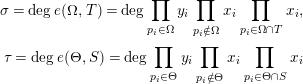$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D70E}=\deg e(\unicode[STIX]{x1D6FA},T)=\deg \mathop{\prod }_{p_{i}\in \unicode[STIX]{x1D6FA}}y_{i}\mathop{\prod }_{p_{i}\notin \unicode[STIX]{x1D6FA}}x_{i}\mathop{\prod }_{p_{i}\in \unicode[STIX]{x1D6FA}\cap T}x_{i}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \unicode[STIX]{x1D70F}=\deg e(\unicode[STIX]{x1D6E9},S)=\deg \mathop{\prod }_{p_{i}\in \unicode[STIX]{x1D6E9}}y_{i}\mathop{\prod }_{p_{i}\notin \unicode[STIX]{x1D6E9}}x_{i}\mathop{\prod }_{p_{i}\in \unicode[STIX]{x1D6E9}\cap S}x_{i} & \displaystyle \nonumber\end{eqnarray}$$

and $\unicode[STIX]{x1D70F}\succ \unicode[STIX]{x1D70E}$ , it follows that

$$\begin{eqnarray}\displaystyle \left\{\begin{array}{@{}l@{}}\unicode[STIX]{x1D6FA}\subset \unicode[STIX]{x1D6E9},\\ (V(\mathfrak{d}_{G})\setminus \unicode[STIX]{x1D6FA})\cup (\unicode[STIX]{x1D6FA}\cap T)\subset (V(\mathfrak{d}_{G})\setminus \unicode[STIX]{x1D6E9})\cup (\unicode[STIX]{x1D6E9}\cap S).\end{array}\right. & & \displaystyle \nonumber\end{eqnarray}$$

By $\unicode[STIX]{x1D6FA}\subset \unicode[STIX]{x1D6E9}$ , we have $(V(\mathfrak{d}_{G})\setminus \unicode[STIX]{x1D6E9})\cap \unicode[STIX]{x1D6FA}=\emptyset$ . Hence $\unicode[STIX]{x1D6FA}\cap T\subset \unicode[STIX]{x1D6E9}\cap S$ . Then $A(\unicode[STIX]{x1D6E9})\supset \unicode[STIX]{x1D6E9}\cap S\supset \unicode[STIX]{x1D6FA}\cap T=A(\unicode[STIX]{x1D6FA})$ , where the last equality follows from the condition (ii). Since $A(\unicode[STIX]{x1D6E9}),A(\unicode[STIX]{x1D6FA})\in \unicode[STIX]{x1D6E5}_{\mathfrak{d}_{G}}$ and $A(\unicode[STIX]{x1D6FA})$ is a facet of $\unicode[STIX]{x1D6E5}_{\mathfrak{d}_{G}}$ by (i), we have $A(\unicode[STIX]{x1D6FA})=A(\unicode[STIX]{x1D6E9})$ . Then it also follows that $\unicode[STIX]{x1D6FA}=\unicode[STIX]{x1D6E9}$ . Again by (ii), this contradicts to $\unicode[STIX]{x1D70F}\succ \unicode[STIX]{x1D70E}$ .◻

Now we can prove Theorem 1.1 for a Cohen–Macaulay very well-covered graph by showing the following proposition and using the Alexander duality: $\operatorname{pd}S/I(G)=\operatorname{reg}J(G)$ given by Terai[18].

Proposition 3.5. Let $G$ be a very well-covered graph. If $\unicode[STIX]{x1D6FD}_{r,\unicode[STIX]{x1D70E}}(J(G))\neq 0$ is extremal, then there exists a pairwise $3$ -disjoint set ${\mathcal{B}}=\{B_{1},\ldots ,B_{r}\}$ of complete bipartite subgraph of $G$ with $V({\mathcal{B}})=\unicode[STIX]{x1D70E}$ .

Corollary 3.6. Let $G$ be a Cohen–Macaulay very well-covered graph. Then

$$\begin{eqnarray}\displaystyle & & \displaystyle \operatorname{pd}S/I(G)=\operatorname{height}I(G)\nonumber\\ \displaystyle & & \displaystyle \quad =\max \left\{\#V({\mathcal{B}})-r:\begin{array}{@{}l@{}}{\mathcal{B}}=\{B_{1},\ldots ,B_{r}\}\text{is a pairwise 3-disjoint set}\\ \text{of complete bipartite subgraphs of }G\end{array}\right\}.\nonumber\end{eqnarray}$$

Since $J(G)$ is squarefree, we only need to consider the case where the degree $\unicode[STIX]{x1D70E}$ is a $(0,1)$ -vector because otherwise $\unicode[STIX]{x1D6FD}_{i,\unicode[STIX]{x1D70E}}(J(G))=0$ . Hence we sometimes identify the degree $\unicode[STIX]{x1D70E}$ with a subset of $V(G)$ .

Proof of Proposition 3.5.

Assume that $\unicode[STIX]{x1D6FD}_{r,\unicode[STIX]{x1D70E}}(J(G))\neq 0$ is extremal. Then there exists a free basis $e(\unicode[STIX]{x1D6FA},T)$ with $\#(\unicode[STIX]{x1D6FA}\cap T)=r$ and $\deg e(\unicode[STIX]{x1D6FA},T)=\unicode[STIX]{x1D70E}$ . Also by Corollary 3.4, $A(\unicode[STIX]{x1D6FA})$ is a facet of $\unicode[STIX]{x1D6E5}_{\mathfrak{d}_{G}}$ and $\unicode[STIX]{x1D6FA}\cap T=A(\unicode[STIX]{x1D6FA})$ holds. Note that

$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70E}=\deg u_{A(\unicode[STIX]{x1D6FA}),T}=\deg \mathop{\prod }_{p_{i}\in \unicode[STIX]{x1D6FA}}y_{i}\mathop{\prod }_{p_{i}\notin \unicode[STIX]{x1D6FA}}x_{i}\mathop{\prod }_{p_{i}\in A(\unicode[STIX]{x1D6FA})}x_{i}. & & \displaystyle \nonumber\end{eqnarray}$$

Set $A(\unicode[STIX]{x1D6FA}):=\{p_{\ell _{1}},\ldots ,p_{\ell _{r}}\}$ . Since $A(\unicode[STIX]{x1D6FA})$ is independent in $\mathfrak{d}_{G}$ , it follows that $\{x_{\ell _{1}},y_{\ell _{1}}\},\ldots ,\{x_{\ell _{r}},y_{\ell _{r}}\}$ are pairwise $3$ -disjoint in $G$ . We define $V_{1}$ to be the set of $z\in V(G)$ which divides $u_{A(\unicode[STIX]{x1D6FA}),T}$ and one of $\{z,x_{\ell _{1}}\},\{z,y_{\ell _{1}}\}$ is an edge of $G$ . Next we define $V_{2}$ to be the set of $z\in V(G)\setminus V_{1}$ which divides $u_{A(\unicode[STIX]{x1D6FA}),T}$ and one of $\{z,x_{\ell _{2}}\},\{z,y_{\ell _{2}}\}$ is an edge of $G$ . Similarly, we define $V_{k}$ to be the set of $z\in V(G)\setminus (V_{1}\cup \cdots \cup V_{k-1})$ which divides $u_{A(\unicode[STIX]{x1D6FA}),T}$ and one of $\{z,x_{\ell _{k}}\},\{z,y_{\ell _{k}}\}$ is an edge of $G$ . As a result, we obtain $V_{1},\ldots ,V_{r}$ . Note that $x_{\ell _{k}},y_{\ell _{k}}\in V_{k}$ .

We prove the following $2$ claims which derive the proposition:

Claim 1. $\unicode[STIX]{x1D70E}=V_{1}\sqcup \cdots \sqcup V_{r}$ .

Claim 2. $G_{V_{k}}$ contains a complete bipartite graph as a spanning subgraph.

Proof of Claim 1. It is clear that $V_{\ell }\cap V_{k}\neq \emptyset$ if $k\neq \ell$ . Also

$$\begin{eqnarray}\displaystyle \{x_{\ell _{1}},\ldots ,x_{\ell _{r}},y_{\ell _{1}},\ldots ,y_{\ell _{r}}\}\subset V_{1}\cup \cdots \cup V_{r}\subset \unicode[STIX]{x1D70E}. & & \displaystyle \nonumber\end{eqnarray}$$

We set $\unicode[STIX]{x1D70E}_{0}:=\unicode[STIX]{x1D70E}\setminus \{x_{\ell _{1}},\ldots ,x_{\ell _{r}},y_{\ell _{1}},\ldots ,y_{\ell _{r}}\}$ . We prove $\unicode[STIX]{x1D70E}_{0}\subset V_{1}\cup \cdots \cup V_{r}$ . Then Claim 1 follows.

If $y_{\ell }\in \unicode[STIX]{x1D70E}_{0}$ , then $p_{\ell }\in \unicode[STIX]{x1D6FA}$ . Therefore, $p_{\ell }\succ p_{\ell _{k}}$ for some $p_{\ell _{k}}\in A(\unicode[STIX]{x1D6FA})$ . This implies $\{x_{\ell _{k}},y_{\ell }\}\in E(G)$ . Therefore, $y_{\ell }\in V_{1}\cup \cdots \cup V_{k}$ .

If $x_{\ell }\in \unicode[STIX]{x1D70E}_{0}$ , then $p_{\ell }\notin \unicode[STIX]{x1D6FA}$ . Note that $p_{\ell }\notin A(\unicode[STIX]{x1D6FA})$ . Since $A(\unicode[STIX]{x1D6FA})$ is a facet of $\unicode[STIX]{x1D6E5}_{\mathfrak{d}_{G}}$ and $A(\unicode[STIX]{x1D6FA})\subsetneq A(\unicode[STIX]{x1D6FA})\cup \{p_{\ell }\}$ , it follows that $A(\unicode[STIX]{x1D6FA})\cup \{p_{\ell }\}\notin \unicode[STIX]{x1D6E5}_{\mathfrak{d}_{G}}$ , in other words, $A(\unicode[STIX]{x1D6FA})\cup \{p_{\ell }\}$ is not independent in $\mathfrak{d}_{G}$ . Since $p_{\ell }\notin \unicode[STIX]{x1D6FA}$ , it follows that $p_{\ell }p_{\ell _{k}}\in E_{d}(\mathfrak{d}_{G})$ for some $k$ or $\{p_{\ell },p_{\ell _{k}}\}\in E_{u}(\mathfrak{d}_{G})$ for some $k$ . In the former case, we have $\{x_{\ell },y_{\ell _{k}}\}\in E(G)$ , and the latter case, we have $\{x_{\ell },x_{\ell _{k}}\}\in E(G)$ . Thus $x_{\ell }\in V_{1}\cup \cdots \cup V_{k}$ .

Proof of Claim 2. For each $k$ , we set

$$\begin{eqnarray}\displaystyle & \displaystyle V_{1k}:=\{z\in V_{k}:\{z,x_{\ell _{k}}\}\in E(G)\}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle V_{2k}:=\{x_{\ell }\in V_{k}:\{x_{\ell },y_{\ell _{k}}\}\in E(G)\}. & \displaystyle \nonumber\end{eqnarray}$$

Note that $V_{1k}\cap V_{2k}=\emptyset$ by the condition (iv) of Theorem 2.1. Also $V_{1k}\cup V_{2k}=V_{k}$ holds. Take $z\in V_{1k}$ and $x_{\ell }\in V_{2k}$ . Since $\{z,x_{\ell _{k}}\},\{x_{\ell },y_{\ell _{k}}\}\in E(G)$ , we have $\{z,x_{\ell }\}\in E(G)$ by the condition (iii) of Theorem 2.1.◻

4 Proof of the main theorem

In this section we prove Theorem 1.1. We use arguments similar to that of [9, Theorem 7.1].

First, we recall some notation. Let $G$ be a very well-covered graph on $V=\{x_{1},\ldots ,x_{h},y_{1},\ldots ,y_{h}\}$ with the properties (i), (ii), (iii), (iv) of Theorem 2.1. Then we obtain the transitively closed semidirected graph $\mathfrak{d}_{G}$ on the vertex set $\{p_{1},\ldots ,p_{h}\}$ . Let ${\mathcal{Z}}_{1},\ldots ,{\mathcal{Z}}_{t}$ be all strongly connected components of $\mathfrak{d}_{G}$ . Then we obtain the acyclic reduction $\widehat{\mathfrak{d}}_{G}$ of $\mathfrak{d}_{G}$ , whose vertex set is $\{q_{1},\ldots ,q_{t}\}$ . The semidirected graph $\widehat{\mathfrak{d}}_{G}$ corresponds to the acyclic reduction $\widehat{G}$ of $G$ . Note that $\widehat{G}$ is a Cohen–Macaulay very well-covered graph and we may assume that the vertex set of $\widehat{G}$ is $\{u_{1},\ldots ,u_{t},v_{1},\ldots ,v_{t}\}$ satisfying (i), (ii), (iii), (iv) of Theorem 2.1 and (v) of Theorem 2.2 (though we need to replace notation $x_{i},y_{j},z_{k}$ by $u_{i},v_{j},w_{k}$ , respectively). Also we set $\unicode[STIX]{x1D701}_{a}=\#{\mathcal{Z}}_{a}$ . Moreover, for $\unicode[STIX]{x1D70E}=\prod _{a}u_{a}^{s_{a}}\prod _{b}v_{b}^{r_{b}}$ , we set $\unicode[STIX]{x1D70E}^{\unicode[STIX]{x1D701}}=\prod _{a}u_{a}^{s_{a}\unicode[STIX]{x1D701}_{a}}\prod _{b}v_{b}^{r_{b}\unicode[STIX]{x1D701}_{b}}$ .

The following result is an extension of the result for unmixed bipartite graphs by Kummini [10, Proposition 3.2] to very well-covered graphs.

Proposition 4.1. Let $G$ be a very well-covered graph. Using the above notation we have

$$\begin{eqnarray}\displaystyle \operatorname{pd}S/I(G)=\max \{|\unicode[STIX]{x1D70E}^{\unicode[STIX]{x1D701}}|-r:\unicode[STIX]{x1D6FD}_{r,\unicode[STIX]{x1D70E}}(J(\widehat{G}))\neq 0\}. & & \displaystyle \nonumber\end{eqnarray}$$

One can prove this proposition by a similar argument due to Kummini [10]. We omit the proof.

Now we prove Theorem 1.1.

Proof of Theorem 1.1.

We use the same notation as above. Let $G$ be a very well-covered graph on $V=\{x_{1},\ldots ,x_{h},y_{1},\ldots ,y_{h}\}$ with the properties (i), (ii), (iii), (iv) of Theorem 2.1.

Take $\unicode[STIX]{x1D6FD}_{r,\unicode[STIX]{x1D70E}}(J(\widehat{G}))\neq 0$ which gives $\operatorname{pd}S/I(G)$ . We may assume that $\unicode[STIX]{x1D6FD}_{r,\unicode[STIX]{x1D70E}}(J(\widehat{G}))$ is extremal. Indeed, suppose that $\unicode[STIX]{x1D6FD}_{r,\unicode[STIX]{x1D70E}}(J(\widehat{G}))$ is not extremal. Then there exist $s\geqslant r$ and $\unicode[STIX]{x1D70F}\supsetneq \unicode[STIX]{x1D70E}$ with $|\unicode[STIX]{x1D70F}|-|\unicode[STIX]{x1D70E}|\geqslant s-r$ satisfying $\unicode[STIX]{x1D6FD}_{s,\unicode[STIX]{x1D70F}}(J(\widehat{G}))\neq 0$ . In this case,

$$\begin{eqnarray}\displaystyle (|\unicode[STIX]{x1D70F}^{\unicode[STIX]{x1D701}}|-s)-(|\unicode[STIX]{x1D70E}^{\unicode[STIX]{x1D701}}|-r) & = & \displaystyle \mathop{\sum }_{u_{a}\in \unicode[STIX]{x1D70F}\setminus \unicode[STIX]{x1D70E}}\unicode[STIX]{x1D701}_{a}+\mathop{\sum }_{v_{b}\in \unicode[STIX]{x1D70F}\setminus \unicode[STIX]{x1D70E}}\unicode[STIX]{x1D701}_{b}-(s-r)\nonumber\\ \displaystyle & {\geqslant} & \displaystyle |\unicode[STIX]{x1D70F}|-|\unicode[STIX]{x1D70E}|-(s-r)\geqslant 0.\nonumber\end{eqnarray}$$

Therefore, we can replace $\unicode[STIX]{x1D6FD}_{r,\unicode[STIX]{x1D70E}}(J(\widehat{G}))$ by $\unicode[STIX]{x1D6FD}_{s,\unicode[STIX]{x1D70F}}(J(\widehat{G}))$ .

Since $\widehat{G}$ is Cohen–Macaulay, we can take a pairwise $3$ -disjoint set $\widehat{{\mathcal{B}}}=\{\widehat{B}_{1},\ldots ,\widehat{B}_{r}\}$ of complete bipartite subgraphs of $\widehat{G}$ with $V(\widehat{{\mathcal{B}}})=\unicode[STIX]{x1D70E}$ as constructed in Proposition 3.5. We can assume that $\{u_{a_{k}},v_{a_{k}}\}\in E(\widehat{B}_{k})$ and $\{u_{a_{1}},v_{a_{1}}\},\ldots ,\{u_{a_{r}},v_{a_{r}}\}$ are pairwise $3$ -disjoint in $\widehat{G}$ . Moreover, we can assume that $\widehat{B}_{k}$ is the complete bipartite subgraph of $\widehat{G}$ on $\widehat{V}_{k}:=V(\widehat{B}_{k})$ which is decomposed as $\widehat{V}_{1k}\sqcup \widehat{V}_{2k}$ , where

$$\begin{eqnarray}\displaystyle & \displaystyle \widehat{V}_{1k}=\{w_{b}\in \widehat{V}_{k}:\{w_{b},u_{a_{k}}\}\in E(\widehat{G})\}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle \widehat{V}_{2k}=\{u_{b}\in \widehat{V}_{k}:\{u_{b},v_{a_{k}}\}\in E(\widehat{G})\}. & \displaystyle \nonumber\end{eqnarray}$$

Set

$$\begin{eqnarray}\displaystyle & \displaystyle V_{1k}:=\left(\mathop{\bigcup }_{u_{b}\in \widehat{V}_{1k}}\{x_{\ell }:p_{\ell }\in {\mathcal{Z}}_{b}\}\right)\cup \left(\mathop{\bigcup }_{v_{b}\in \widehat{V}_{1k}}\{y_{\ell }:p_{\ell }\in {\mathcal{Z}}_{b}\}\right), & \displaystyle \nonumber\\ \displaystyle & \displaystyle V_{2k}:=\mathop{\bigcup }_{u_{b}\in \widehat{V}_{2k}}\{x_{\ell }:p_{\ell }\in {\mathcal{Z}}_{b}\}. & \displaystyle \nonumber\end{eqnarray}$$

Since $\widehat{V}_{1k}\cap \widehat{V}_{2k}=\emptyset$ , we have $V_{1k}\cap V_{2k}=\emptyset$ . Note that for each $b$ , at least one of $u_{b}$ and $v_{b}$ is not contained in $\widehat{V}_{1k}$ . Let $B_{k}$ be the complete bipartite graph with the bipartition $V_{1k}\sqcup V_{2k}$ . Set ${\mathcal{B}}:=\{B_{1},\ldots ,B_{r}\}$ . It is clear that $V(B_{k})\cap V(B_{\ell })=\emptyset$ for $k\neq \ell$ and $\#V({\mathcal{B}})=|\unicode[STIX]{x1D70E}^{\unicode[STIX]{x1D701}}|$ . We prove the following $2$ claims which derive the theorem.

Claim 1. $B_{k}$ is a subgraph of $G$ .

Claim 2. ${\mathcal{B}}$ is pairwise $3$ -disjoint in $G$ .

Proof of Claim 1. Take $\{z_{\ell },x_{m}\}\in E(B_{k})$ , where $z_{\ell }\in V_{1k}$ and $x_{m}\in V_{2k}$ . Then there exist $w_{a}\in \widehat{V}_{1k}$ and $u_{b}\in \widehat{V}_{2k}$ such that $p_{\ell }\in {\mathcal{Z}}_{a}$ and $p_{m}\in {\mathcal{Z}}_{b}$ .

We first assume $a=b$ . Since $w_{a}\in \widehat{V}_{1k}$ , $u_{a}\in \widehat{V}_{2k}$ , and $\widehat{V}_{1k}\cap \widehat{V}_{2k}=\emptyset$ , it follows that $w_{a}=v_{a}$ and thus $z_{\ell }=y_{\ell }$ . On the other hand, $p_{\ell },p_{m}\in {\mathcal{Z}}_{a}$ . In particular, $p_{m}p_{\ell }\in E_{d}(\mathfrak{d}_{G})$ . This means $\{x_{m},y_{\ell }\}\in E(G)$ as desired.

We next assume $a\neq b$ . If $z_{\ell }=x_{\ell }$ , then $w_{a}=u_{a}$ and we have $\{q_{a},q_{b}\}\in E_{u}(\widehat{\mathfrak{d}}_{G})$ since $\{u_{a},u_{b}\}\in E(\widehat{B}_{k})\subset E(\widehat{G})$ . Therefore, $\{p_{\ell },p_{m}\}\in E_{u}(\mathfrak{d}_{G})$ . This means that $\{z_{\ell },x_{m}\}=\{x_{\ell },x_{m}\}\in E(G)$ . If $z_{\ell }=y_{\ell }$ , then $w_{a}=v_{a}$ and we have $q_{b}q_{a}\in E_{d}(\widehat{\mathfrak{d}}_{G})$ since $\{v_{a},u_{b}\}\in E(\widehat{B}_{k})\subset E(\widehat{G})$ . Therefore, $p_{m}p_{\ell }\in E_{d}(\mathfrak{d}_{G})$ . This means that $\{z_{\ell },x_{m}\}=\{y_{\ell },x_{m}\}\in E(G)$ .

Proof of Claim 2. Recall that $\{u_{a_{1}},v_{a_{1}}\},\ldots ,\{u_{a_{r}},v_{a_{r}}\}$ are pairwise $3$ -disjoint in $\widehat{G}$ . Let $p_{\ell _{s}}\in {\mathcal{Z}}_{a_{s}}$ . Then $\{x_{\ell _{1}},y_{\ell _{1}}\},\ldots ,\{x_{\ell _{r}},y_{\ell _{r}}\}$ are pairwise $3$ -disjoint in $G$ .◻

5 Projective dimension of symbolic powers of the edge ideal of a very well-covered graph

In this section we show that the projective dimension of symbolic powers of the edge ideal of a very well-covered graph is nondecreasing.

We recall the definition of a symbolic power of an ideal.

Let $I$ be a radical ideal of a polynomial ring $S$ . Let $\operatorname{Min}_{S}(S/I)=\{P_{1},\ldots ,P_{r}\}$ be the set of the minimal prime ideals of $I$ , and put $W=S\setminus \bigcup _{i=1}^{r}P_{i}$ . Given an integer $\ell \geqslant 1$ , the $\ell$ th symbolic power of $I$ is defined to be the ideal

$$\begin{eqnarray}I^{(\ell )}=I^{\ell }S_{W}\cap S=\mathop{\bigcap }_{i=1}^{r}P_{i}^{\ell }S_{P_{i}}\cap S.\end{eqnarray}$$

In particular, if $I$ is a squarefree monomial ideal of $S$ , then one has

$$\begin{eqnarray}I^{(\ell )}=P_{1}^{\ell }\cap \cdots \cap P_{r}^{\ell }.\end{eqnarray}$$

We use the following lemma:

Lemma 5.1. [14, Corollary 1.3]

Let $I$ be a monomial ideal in a polynomial ring $S$ . Take a monomial $m$ such that $m\not \in I$ . Then

$$\begin{eqnarray}\operatorname{depth}S/(I:m)\geqslant \operatorname{depth}S/I.\end{eqnarray}$$

Now we state the main result in this section.

Theorem 5.2. Let $G$ be a very well-covered graph or a graph with a leaf. Then for $i\geqslant 2$ ,

$$\begin{eqnarray}\operatorname{pd}S/I(G)^{(i)}\geqslant \operatorname{pd}S/I(G)^{(i-1)}.\end{eqnarray}$$

Proof. Let $P$ be a minimal prime ideal of $I(G)$ . We first assume that $G$ is a very well-covered graph whose vertices are labeled as in Theorem 2.1. Then $P$ is of the form

$$\begin{eqnarray}P=(z_{1},z_{2},\ldots ,z_{h})\end{eqnarray}$$

where $z_{i}=x_{i}$ or $z_{i}=y_{i}$ for $i=1,2,\ldots ,h$ by [2, Corollary 2.2].

Next we assume that $G$ has a leaf $x_{1}$ . And we assume that $\{x_{1},y_{1}\}\in E(G)$ . Then just either one of $x_{1}$ and $y_{1}$ is contained in $P$ .

In either case we show that

$$\begin{eqnarray}P^{i}:x_{1}y_{1}=P^{i-1}.\end{eqnarray}$$

Take a minimal monomial generator $m$ of $P^{i}$ . Then $m$ is not divided by $x_{1}y_{1}$ and $x_{1}y_{1}\in P$ . Hence $(m):x_{1}y_{1}\subset P^{i-1}$ . Hence $P^{i}:x_{1}y_{1}\subset P^{i-1}$ . Conversely, take a minimal monomial generator $m$ of $P^{i-1}$ . Since we have $x_{1}\in P$ or $y_{1}\in P$ , we have $mx_{1}y_{1}\in P^{i}$ . Then we have $P^{i-1}\subset P^{i}:x_{1}y_{1}$ .

Now we have

$$\begin{eqnarray}\displaystyle I(G)^{(i)}:x_{1}y_{1} & = & \displaystyle \left(\mathop{\bigcap }_{P\in \operatorname{Min}_{S}S/I(G)}P^{i}\right):x_{1}y_{1}\nonumber\\ \displaystyle & = & \displaystyle \mathop{\bigcap }_{P\in \operatorname{Min}_{S}S/I(G)}(P^{i}:x_{1}y_{1})\nonumber\\ \displaystyle & = & \displaystyle \mathop{\bigcap }_{P\in \operatorname{Min}_{S}S/I(G)}P^{i-1}\nonumber\\ \displaystyle & = & \displaystyle I(G)^{(i-1)}.\nonumber\end{eqnarray}$$

By Lemma 5.1 we have

$$\begin{eqnarray}\displaystyle \operatorname{pd}S/I(G)^{(i)} & {\geqslant} & \displaystyle \operatorname{pd}S/(I(G)^{(i)}:x_{1}y_{1})\nonumber\\ \displaystyle & = & \displaystyle \operatorname{pd}S/I(G)^{(i-1)}.\square\nonumber\end{eqnarray}$$

As an application we show that the projective dimension of the ordinary powers of the edge ideal is also nondecreasing for certain bipartite graphs.

Corollary 5.3. Let $G$ be an unmixed or sequentially Cohen–Macaulay bipartite graph. Then for $i\geqslant 2$ ,

$$\begin{eqnarray}\operatorname{pd}S/I(G)^{i}\geqslant \operatorname{pd}S/I(G)^{i-1}.\end{eqnarray}$$

The above corollary follows from the next facts:

Lemma 5.4. [15, Lemma 3.10], [16, Lemma 5.8, Theorem 5.9]

Let $I(G)$ be the edge ideal of a graph $G$ . Let $t\geqslant 2$ be an integer. Then $I(G)^{(t)}=I(G)^{t}$ holds if and only if $G$ contains no odd cycles of length $2s-1$ for any $2\leqslant s\leqslant t$ .

Lemma 5.5. [20, Lemma 2.8]

Let $G$ be a sequentially Cohen–Macaulay bipartite graph. Then $G$ has a leaf.

Remark 5.6. Using the corresponding result to Lemma 5.1 for Stanley depth $\operatorname{sdepth}$ instead of depth in [1], we can prove the following nonincreasing property of Stanley depth, similarly:

1. (1) $\operatorname{sdepth}S/I(G)^{(i)}\leqslant \operatorname{sdepth}S/I(G)^{(i-1)}$ for a very well-covered graph $G$ with $i\geqslant 2$ .

2. (2) $\operatorname{sdepth}S/I(G)^{i}\leqslant \operatorname{sdepth}S/I(G)^{i-1}$ for an unmixed or sequentially Cohen–Macaulay bipartite graph $G$ with $i\geqslant 2$ .