Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-26T07:22:33.206Z Has data issue: false hasContentIssue false
  • English
  • Français

Rational double points on a normal octic K3 surface

Published online by Cambridge University Press:  22 January 2016

Li-Zhong Tang
Li-Zhong Tang*
Affiliation:
Department of Mathematics, Graduate School of Academia Sinica, Beijing 100039, P. R. China
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let S be a normal surface of degree n in 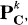, where (n, k) = (4,3), (6,4) or (8,5). People try to describe all possible combinations of singularities on such surfaces. The case (4,3) is already very complicated. Using properties of K3 surface and elementary transformations of Dynkin Graphs effectively, Urabe [17] was able to solve the problem partially when all singularities are rational double points.

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 129 , March 1993 , pp. 147 - 177
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1993

References

[1] Artin, M., On isolated rational singularities of surface, Amer Math J., 88 (1966).CrossRefGoogle Scholar
[2] Barth, W., Peters, C., and Vande Ven, A., Compact complex surfaces, Berlin-Heidelberg-New York, Springer, 1984.Google Scholar
[3] Beauville, R., Complex algebraic surfaces, Cambridge University Press, Cambridge, 1983.Google Scholar
[4] Bourbaki, N., Groupes et algebre de Lie, chaps. 4–6, Paris; Herman, 1968.Google Scholar
[5] Conway, J.H. and Sloane, N.J.A., Sphere packings and groups, Berlin-Heidelberg-New York, Springer, 1988.Google Scholar
[6] Durfee, A.H., Fifteen characterization of rational double points and simple critical points, Lengein, Math., II 25 (1979), 131–163.Google Scholar
[7] Dynkin, E.B., Semisimple subalgebras of semisimple Lie groups, Amer. Math. Soc. Transl., 6 (1957), 111–244.Google Scholar
[8] Humphreys, J.E., Introduction to Lie algebra and representatives theory, New York-Heidelberg-Berlin, Springer, 1972.CrossRefGoogle Scholar
[9] Kawamata, Y., A generalization of Kodaira-Ramanujams vanishing theorem, Math. Ann., 261 (1982), 43–46.Google Scholar
[10] Milnor, J. and Husemoller, D., Symmetric bilinear forms, Berlin-Heidelberg-New York, Springer, 1972.Google Scholar
[11] Mumford, D., Algebraic Geometry. Complex projective varieties, Berlin-Heidelberg-New York, Springer, 1976.Google Scholar
[12] Nikulin, V.V., Integral symmetric bilinear forms and some of their applications, Math. USSR, IV 14 (No.1) (1987), 103–167.Google Scholar
[13] Saint-Donat, B., Projective models of K 3 surfaces, Amer. J. Math., 96 (1976) 602–639.Google Scholar
[14] Serre, J.-P., Cours d’arithmétique, Paris Presses univ. France, 1970.Google Scholar
[15] Siu, Y.-T., Every K 3 surface is Kähler, Invent, Math., 73 (1983), 139–150.Google Scholar
[16] Urabe, T., Dynkin Graphs and Quadrilateral Singularities, to appear.CrossRefGoogle Scholar
[17] Urabe, T., Elementary transformations of Dynkin Graph and singularities on quartic surfaces, Invent. Math., 87 (1987), 549–572.Google Scholar
[18] Yang, J.-G., Rational double points on a normal quintic K 3 surface, to appear.Google Scholar