Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
León-Cardenal, Edwin
2022.
𝑝-Adic Analysis, Arithmetic and Singularities.
Vol. 778,
Issue. ,
p.
3.

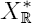 to a connected component
to a connected component 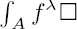 or equivalently the asymptotics when
or equivalently the asymptotics when 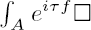 . A topological construction of Γ(
. A topological construction of Γ(